擾動線運動對慣性系粗對準影響分析及優化方法
唐 苗, 劉 暢
(1.海軍裝備部駐北京地區第三軍事代表室,北京 100074;2.北京自動化控制設備研究所,北京 100074)
0 引言
通過粗對準快速確定一個滿足小角度假設的初始姿態矩陣,是進入精對準流程的前提條件,并且其對準精度、速度及對載體運動的約束大小直接影響了武器系統的響應快速性、環境適應性等作戰能力。
目前常用的粗對準方法包括解析式粗對準和慣性系粗對準等。解析式粗對準通過加速度計和陀螺儀測量重力加速度以及地球自轉角速度在載體坐標系的投影,利用雙矢量定姿原理求解載體初始姿態矩陣。該方法要求載體靜止,對擾動加速度和角速度較為敏感,因此使用十分受限。
慣性系粗對準由于不受載體自身角運動影響而得到廣泛應用,最早由秦永元、嚴恭敏等提出,巧妙運用了慣性空間凝固假設,并采用對重力加速度積分的方法,消除了周期性的晃動干擾加速度影響。目前,國內外在慣性系粗對準算法方面已經取得了諸多成果。
雖然慣性系粗對準可以較好地抑制角運動的干擾,但也存在受線振動影響大的問題。趙長山等通過對重力加速度積分矢量進行線性最小二乘擬合,對粗對準過程中的擾動進行抑制,提高了在線振動環境下粗對準的精度。夏家和提出了一種采用分段積分和q-method方法提取足夠多的加速度計量測信息,將姿態矩陣的求解問題轉換為求解Wahba問題,提高了粗對準的魯棒性。此外,文獻[11-12]采用低通濾波器抑制線運動干擾;文獻[13-15]采用濾波算法提高對準精度。
本文通過分析慣性系下重力加速度積分矢量及利用其構造的速度矢量矩陣的物理含義,定量地分析出擾動線運動對粗對準的影響;在此基礎上給出了基于位移積分矢量構造定姿矢量矩陣的慣性系粗對準的優化方法,并通過試驗數據仿真分析進行了驗證。
1 慣性系粗對準分析
本文涉及的坐標系定義如下:
1)地理坐標系(系):即北天東坐標系;
2)慣導體坐標系(系):前上右坐標系;
3)地理慣性坐標系(系):粗對準開始時刻地理坐標系凝固得到的慣性坐標系;
4)慣導慣性體坐標系(系):粗對準開始時刻慣導體坐標系凝固得到的慣性坐標系。
為了便于分析,引入一個新的慣性坐標系系,則慣性系粗對準變為以下3個矩陣的求解過程
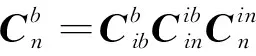
(1)
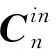
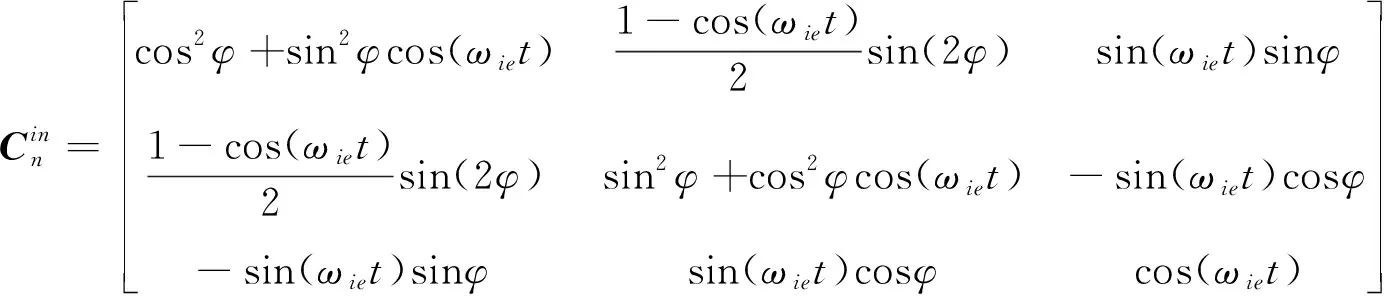
(2)
式中,為慣導系統當地緯度;為地球自轉角速度;為粗對準時間。
由此,可得系下重力的矢量形式
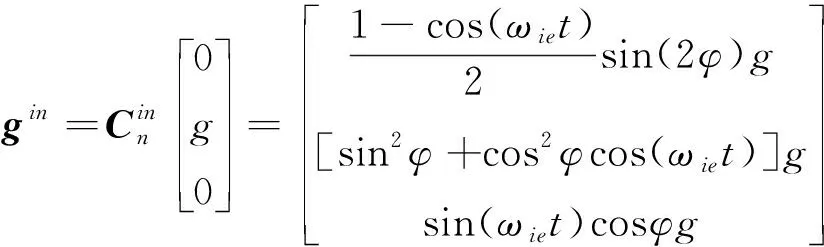
(3)
當粗對準時間較短時,可認為是小量,從而式(3)可化簡為
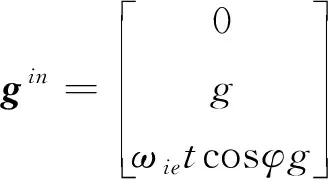
(4)

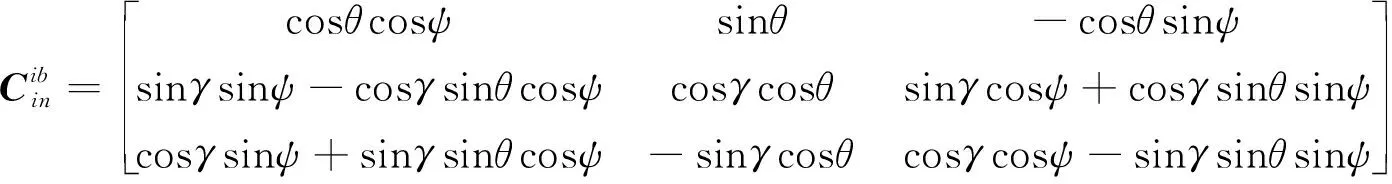
(5)
則重力在系下的投影可寫為
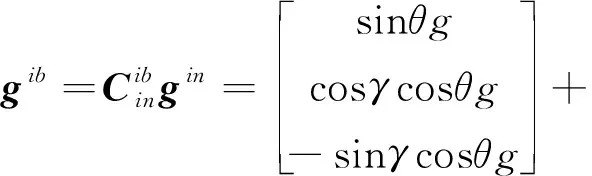
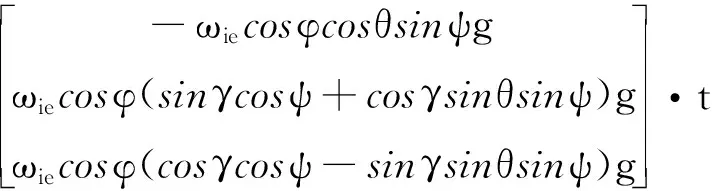
(6)
為防止擾動加速度及加表噪聲等因素影響,對進行積分
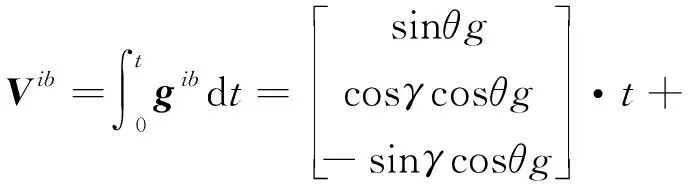
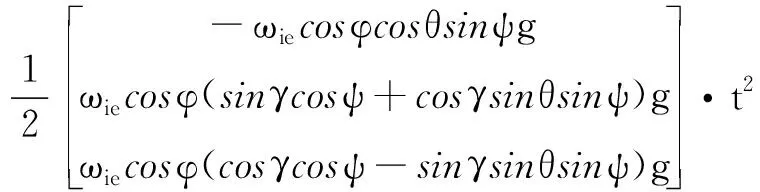
(7)
從式(7)可以看出,一次項中包含了水平姿態信息,二次項中包含了航向信息。而當選取2個時間點的信息構建速度矢量矩陣時,相當于確定了的一次項和二次項(隱含粗對準開始時刻為0的條件)。假設在任意時刻的噪聲水平相當時,選取的時間間隔越大,計算得到的一次項系數和二次項系數將越精確。因此,在選取時間點時通常選擇粗對準時間及粗對準時間的一半,這樣加上初始時刻三點間間隔最為合理。
在利用三點辨識一次項、二次項系數時,相當于解三元一次方程組
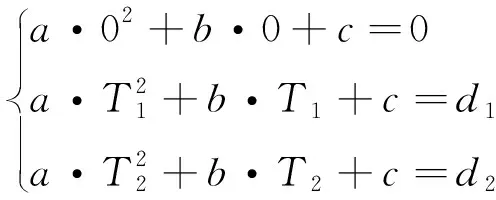
(8)
式中,、分別為粗對準時間長度的一半和粗對準時間;、分別為、時刻重力加速度矢量積分結果。
代入=2,可得
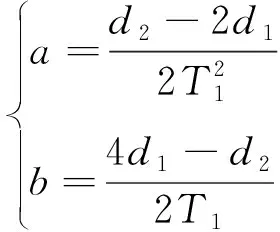
(9)
2 擾動線運動對粗對準影響分析
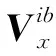
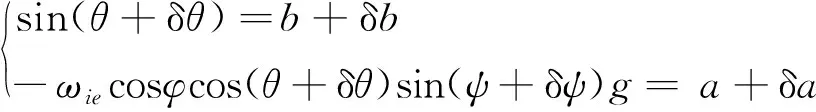
(10)
即
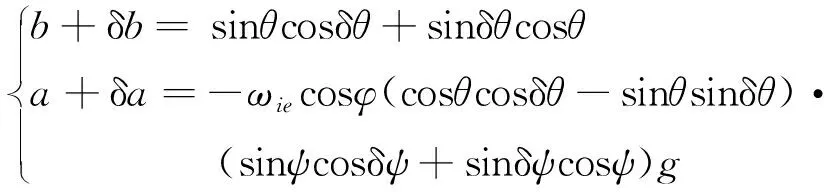
(11)
不妨假設載體姿態接近水平,則式(11)可進一步簡化為
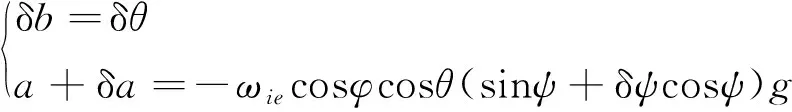
(12)
從而可得
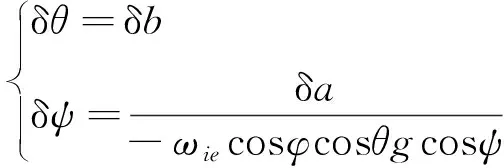
(13)
代入式(9),可得
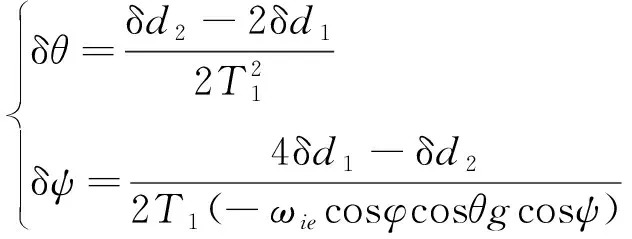
(14)
隨后對某型中高精度捷聯慣導系統靜態對準數據進行仿真,慣導真實航向采用實際精對準結果180.48°,結果如表1所示。
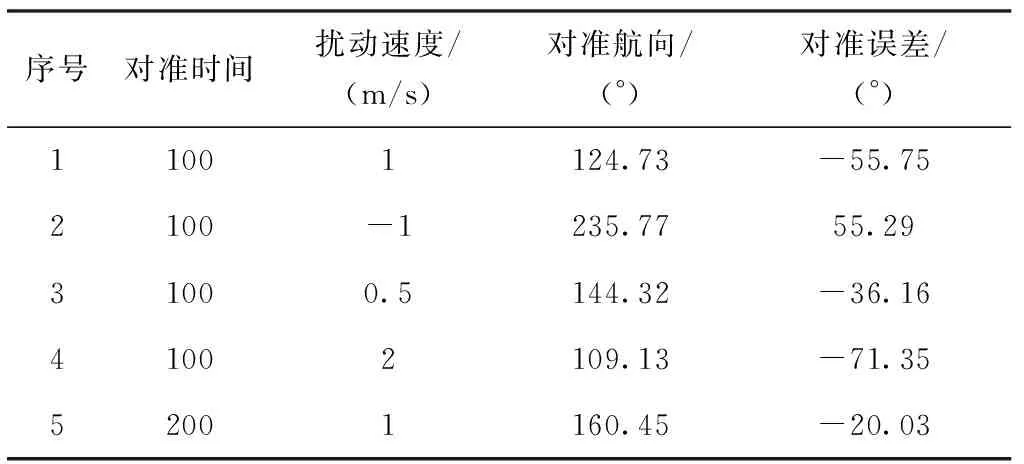
表1 擾動速度對航向影響仿真結果
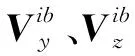
3 針對擾動線運動的粗對準優化方法
從前面的分析可以看出,擾動線運動對慣導系統粗對準精度的影響非常大,而慣導系統實際應用場景,如垂直發射、水面風浪及車輛行駛等動態環境下可能存在較大的真實速度,因此需要對慣性系粗對準算法進行一些改進。
慣性系粗對準算法在構造速度矢量矩陣時,只用了2個時間點的信息
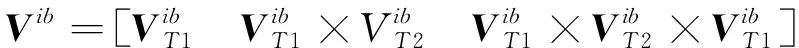
(15)
舍棄了其他時間點大量的速度積分信息,因此對擾動速度極其敏感。目前成熟的方法是通過最小二乘擬合重力積分矢量并用擬合參數重構速度矢量矩陣,該方法需要保存大量的數據信息,同時軟件中增加了較多計算量。此外,該方法成立需滿足一定前提條件:重力加速度積分矢量近似可表示為時間的多項式。從前文公式推導中可知,式(7)是在式(2)的基礎上,即載體位置未發生變化的假定條件下推導得來。當載體處于運動狀態時,由=+可知,若載體不是勻速直線運動,的積分結果就不是嚴格的時間的多項式形式。因此,若在運動狀態下使用,需要動態條件遠小于地球自轉影響。以緯度60°為例,地表相對慣性系速度約為232m/s,因此載體運動速度應不大于23m/s。
考慮到實際對準期間線振動、角振動等條件下載體位置振動有限,本文采用對速度積分矢量進一步積分的方法抑制周期性的擾動加速度和線速度對粗對準的影響。
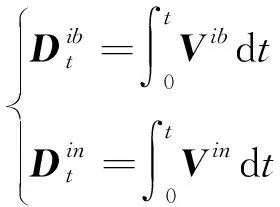
(16)
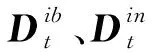
此外,在構造位移矢量矩陣時,利用3個時間點的位移積分信息
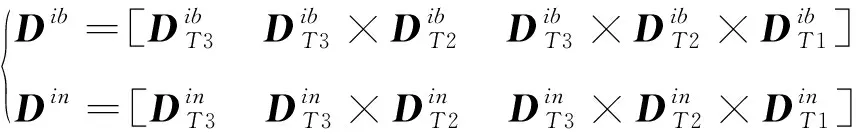
(17)
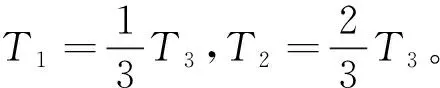
對于動態條件下動基座粗對準,當有里程計等外部速度信息輸入時,可以通過式(18)進行積分
=
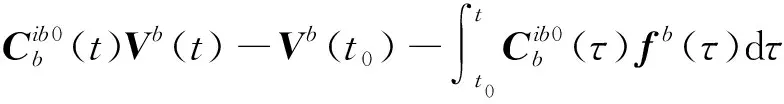
(18)
當有衛星等外界地理坐標系速度信息情況下,可以通過式(19)對進行積分
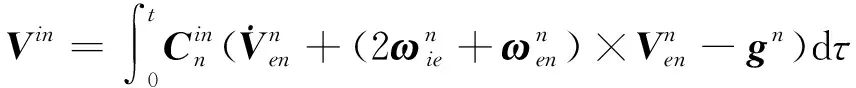
(19)
4 仿真驗證
在上文某型捷聯慣導系統靜態對準數據的基礎上增加一個周期0.3s、大小為1m/s的余弦加速度,再用兩種粗對準方法進行仿真對比,結果如圖1~圖3所示。

圖1 兩種算法航向角對準結果Fig.1 Course angle results of two algorithms
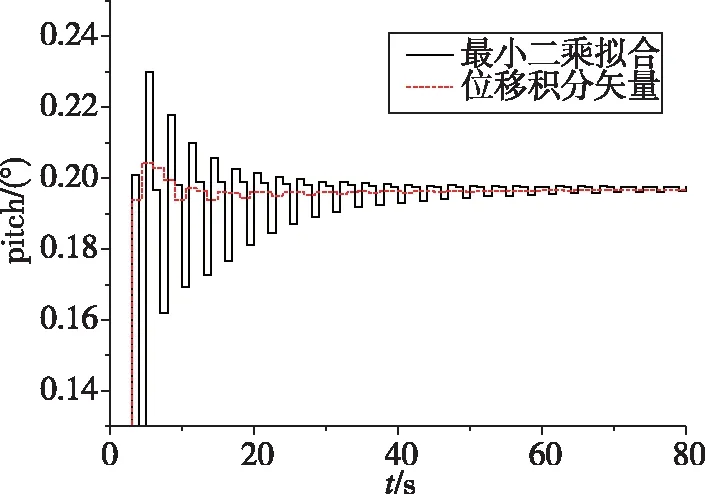
圖2 兩種算法俯仰角對準結果Fig.2 Pitch angle results of two algorithms
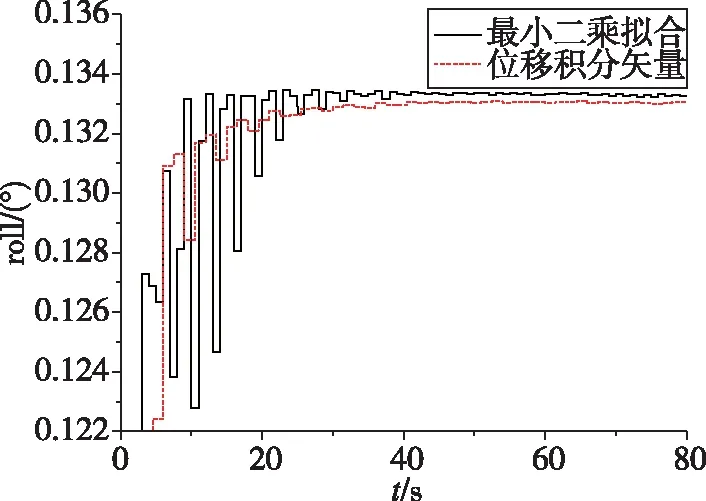
圖3 兩種算法滾動角對準結果Fig.3 Roll angle results of two algorithms
隨后對該型慣導系統搖擺試驗進行仿真,試驗條件為搖擺幅度3°,搖擺頻率1Hz,擾動線運動速度幅值約為0.35m/s,仿真結果如圖4所示。
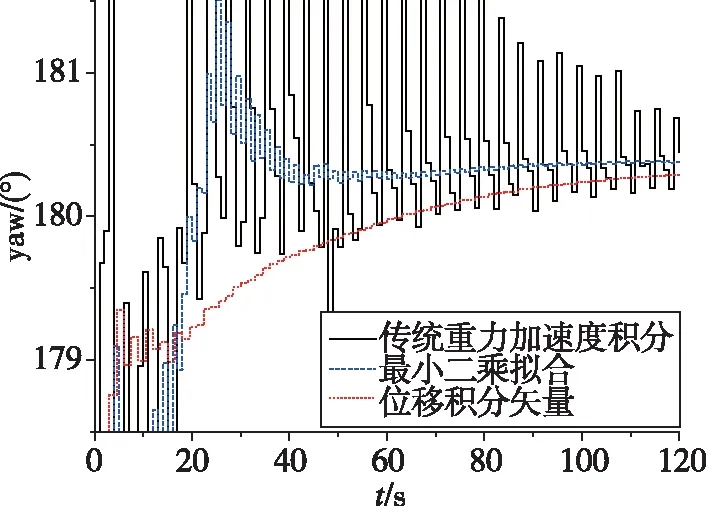
圖4 搖擺試驗仿真結果Fig.4 Simulation result of rolling test
從仿真結果可以看出,本文提出的位置積分矢量法雖然收斂速度比速度積分矢量最小二乘擬合法稍慢,但其對準結果的振幅受擾動線運動影響小,且精度與重力矢量積分法相比大幅提升,能夠滿足精對準使用要求。
5 結論
本文針對擾動線運動對粗對準精度影響較大的問題,提出了一種基于位移積分矢量的抗擾動粗對準算法,算法分析和仿真結果表明:
1)傳統的慣性系抗擾動粗對準相當于用2個時間點的速度積分矢量進行最小二乘二次擬合,擾動線運動通過影響時間多次項參數辨識引入粗對準誤差;
2)采用位移矢量積分的方式代替速度積分矢量進行最小二乘擬合,可以有效減少軟件對處理器數據存儲、運算速率的需求;
3)通過試驗數據仿真分析可知,本文提出的基于位移積分矢量的抗擾動粗對準算法可有效抑制擾動線運動的影響,能較快收斂到滿足精對準使用的粗對準精度。

