空天飛行器星敏感器安裝誤差在線標定方法

安競軻，熊 智，王 融，康 駿，張新睿，劉建業

(南京航空航天大學自動化學院，南京 211106)

0 引言

空天飛行器因其空地往返和可重復利用的特性而具有重要的戰略意義。空天飛行器導航關鍵技術是實現其智能自主控制的核心技術，星敏感器作為空天飛行器組合導航系統中的傳感器之一，通過觀測恒星矢量解算載體姿態，由于其獨有的隱蔽性和自主性，已經廣泛地應用于衛星、飛船等在軌航天器中，對空天飛行器發射段和入軌段的自主導航具有重要作用。星敏感器自身輸出的姿態精度可以達到角秒級，與慣性導航傳感器組合能夠有效抑制慣導姿態發散。但星敏感器的安裝誤差作為決定天文導航精度的主要因素之一，限制了空天飛行器一體化安裝的慣性/天文組合導航系統的定姿和定位性能。

目前，星敏感器安裝誤差的標定與校正主要在起飛前地面上完成，文獻[3]和文獻[4]給出了利用星模擬器和方位基準相互配合對星敏安裝誤差進行標定的方法;文獻[5]提出了星敏安裝誤差的三位置地面標定方法，以上方法均能精確地標定出星敏安裝誤差。但是，空天飛行器執行一次任務往往長達幾百天，歷經發射、在軌和再入3個任務階段。一體化的慣性/天文導航系統中，星敏感器固聯在載體上，由于發射過程中的振動、沖擊、溫度劇變等因素影響，以及隨著長時間累積的安裝角漂移，會使星敏感器發生角位移，導致其安裝誤差角可能達到角分級。因此，需要在載體起飛后，對星敏安裝誤差進行在線標定與實時校正，最大程度地隔離掉安裝誤差對組合導航系統的影響，保證組合導航系統輸出的精度和可靠性。

文獻[8]和文獻[9]都提出了一種基于卡爾曼濾波的星敏安裝誤差快速標定方法，觀測量為慣性/天文姿態信息，能夠快速地標定出星敏安裝誤差；文獻[10]基于星矢量觀測利用卡爾曼濾波對星敏安裝誤差進行了標定，并分析了大、小視場下不同的標定效果；文獻[11]提出了一種基于最小二乘法的星敏安裝誤差在線估計方法，利用估計殘差統計特征量驗證了算法的有效性;文獻[12]提出了一種基于粒子群尋優的高精度星敏感器在軌標定方法，這種方法不依賴陀螺信息，提高了數據的準確性。

本文提出了一種基于恒星矢量觀測的星敏安裝誤差在線標定與校正方法，將慣導姿態誤差角與星敏安裝誤差角關聯，將星光觀測量與姿態、位置誤差關聯,并建立了系統狀態與量測模型，通過卡爾曼濾波實現了對星敏安裝誤差角的在線標定與校正，并通過仿真驗證了算法的有效性。

1 動態標定總體方案

星敏感器安裝誤差在線動態標定的總體方案設計如圖1所示。本文選用大視場星敏感器和捷聯慣導系統，首先建立包含慣導傳統誤差和星敏安裝誤差在內的卡爾曼濾波器狀態方程，量測值由根據慣導系統輸出信息計算出的相對于計算地理坐標系下的高度角和方位角的差值與星敏感器直接觀測到的高度角和方位角構成。通過卡爾曼濾波算法對星敏安裝誤差進行實時估計，從而降低組合導航系統誤差。

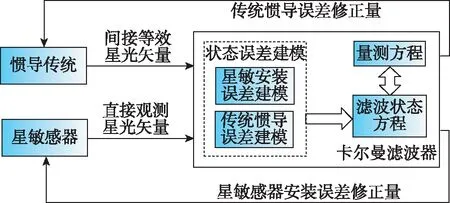
圖1 方案框架圖Fig.1 Scheme frame diagram

2 動態標定慣性、天文安裝誤差模型

2.1 星敏感器與捷聯慣導系統安裝誤差角定義

由于空天飛行器高動態、長航時的運動特性，任務過程中的振動、沖擊和溫度變化均會引起星敏感器安裝位置的偏移，同時隨著時間累積，安裝位置也會發生一定程度的緩慢漂移。綜合以上情況，可將星敏感器的安裝誤差歸納為兩種類型，如圖2所示，一種是位移誤差，一種是角度誤差。由于空天飛行器中星敏感器主要起定姿功能，并忽略小位移引起的桿臂效應的變化，可以認為在飛行過程中只有沿著3個軸向的安裝角度誤差會對導航輸出產生影響，針對安裝角度誤差，使用以下建模方法。

(a)位移誤差

(b)角度誤差

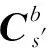
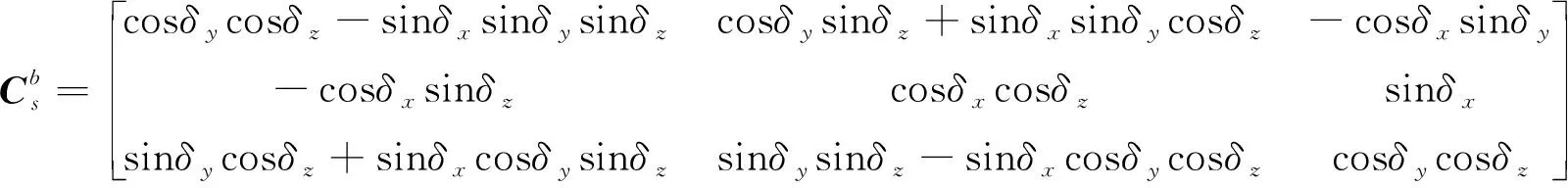
(1)

經過小角度近似得

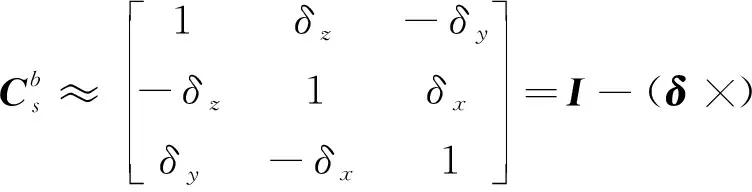
其中，×是的反對稱矩陣

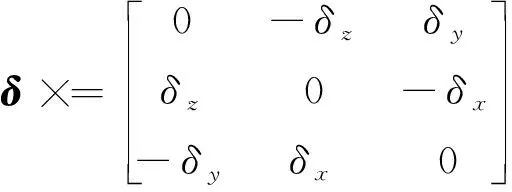
2.2 基于星矢量量測的觀測方程

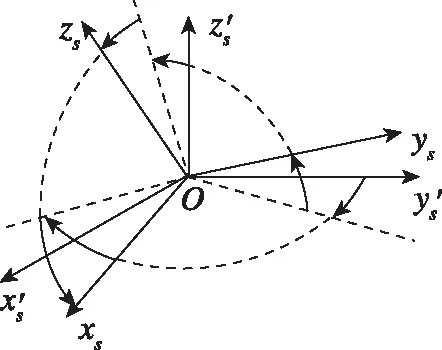
恒星觀測矢量與天文導航觀測角度的定義如圖3所示。在坐標系-中，軸所在平面繞軸反向旋轉角度定義為天文觀測方位角，旋轉后的中間坐標系定義為-；軸繞軸旋轉角度定義為天文觀測高度角，旋轉后坐標系定義為-，旋轉后軸即為星敏感器的光軸。在參考坐標系下,由天文觀測角表示的星矢量為

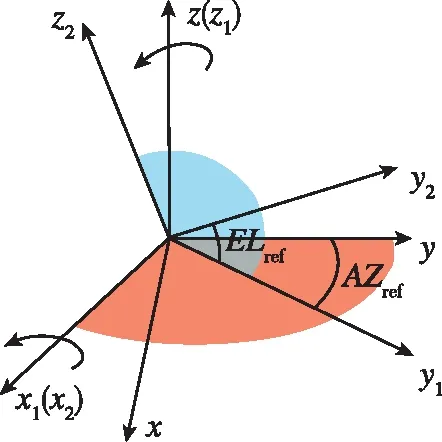
圖3 天文觀測角度定義Fig.3 Astronomical observation angle definition

=[sincoscoscossin]

(2)

式中，為單位星矢量；在參考坐標系下，為天文觀測方位角，為天文觀測高度角。

2.3 天文觀測角與星敏安裝誤差角關系推導

將等效慣性平臺坐標系下的星光矢量記為

=

[sincoscoscossin]

(3)

表示真實地理坐標系下觀測到的星光矢量

=[sincoscoscossin]

(4)

假設相較于真實地理坐標系下的星光矢量存在著由星慣安裝誤差角導致的誤差，即

=+Δ,=+Δ

(5)

將慣導平臺誤差角記為=[]，則從坐標系到坐標系的轉換矩陣為

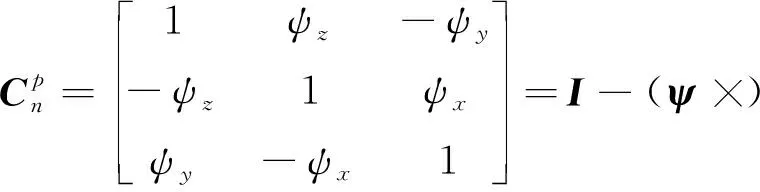
(6)

其中，×是的反對稱矩陣。

同時，星敏感器坐標系下因安裝誤差角引起的慣導平臺誤差角有如下轉換方式

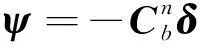
(7)

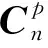
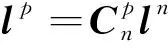
(8)

將式(3)、式(4)、式(5)和式(6)的值代入式(8)后得到

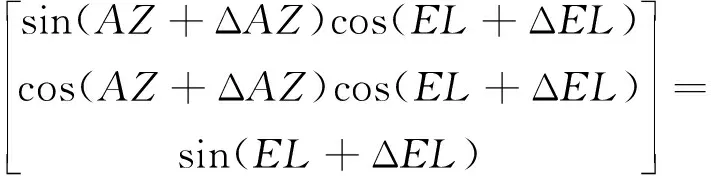
(9)

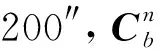
例，計算得到方位角誤差Δ為-9.1″，高度角誤差Δ為10.8″，證明了角分級的安裝誤差引起的方位角和高度角誤差往往在角秒級水平，進而可對其進行小角度近似并忽略高次項誤差，得到如下假設

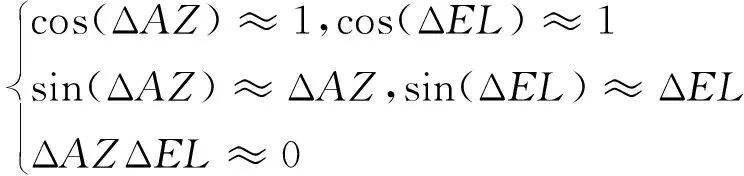
(10)

根據以上假設，由式(9)可以得到天文觀測角誤差和平臺誤差角的關系

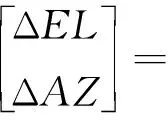
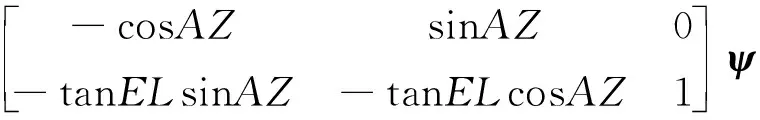
(11)

綜合式(7)和式(11)可得

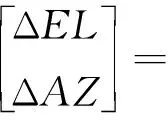
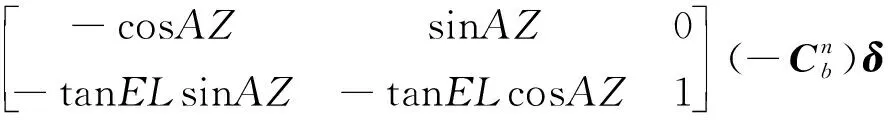
(12)

3 星敏感器安裝誤差標定方法

3.1 系統方程

利用線性卡爾曼濾波器進行組合，系統的狀態方程和量測方程為

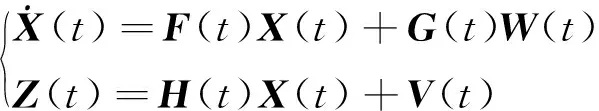
(13)

式中，()為卡爾曼濾波狀態變量；()為卡爾曼濾波系統矩陣；()為狀態變量噪聲矩陣；()為卡爾曼濾波觀測量；()為卡爾曼濾波觀測矩陣；()為觀測噪聲。

(1)卡爾曼濾波狀態方程

常規的卡爾曼濾波狀態模型通常選用慣導系統的輸出參數誤差，分別為3個數學平臺誤差角(,,)、3個速度誤差(δ,δ,δ)和3個位置誤差(δ,δ,δ)；參考文獻[16]中將慣性測量單元(Inertial Measurement Unit, IMU)的隨機漂移誤差(,,,,,,,,)這9個誤差量作為陀螺儀和加速度計的誤差量。基于第2節動態標定星敏安裝誤差模型，在已有濾波模型的基礎上增加3個星敏安裝誤差(,,)，共21個參數作為系統的狀態量，即

=[δδδδδ

δ

]

結合第2節星敏感器安裝誤差角與慣導數學平臺誤差角的轉換關系，建立狀態空間表達式

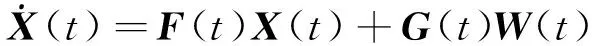
對應的系統矩陣()為

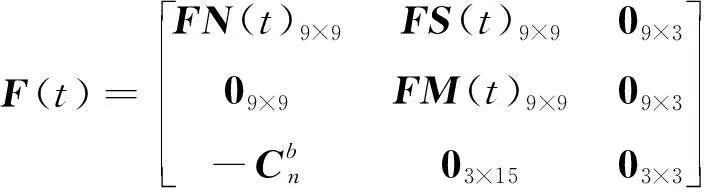
(14)

式中，()為基本導航參數變換矩陣；()為基本導航參數和慣導隨機誤差參數變換矩陣；()為IMU誤差之間的關系矩陣。

3.2 量測方程

參考文獻[17]可知，計算地理坐標系(系)與當地地理坐標系(系)之間考慮有小角度經緯度位置偏差δ、δ時，天文觀測角誤差與經緯度誤差有如下關系

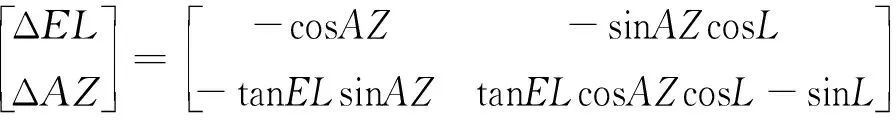
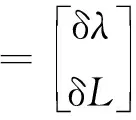
(15)

結合式(11)和式(12)有以下系統量測方程

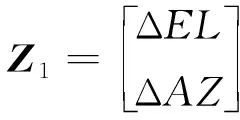
(16)

其中

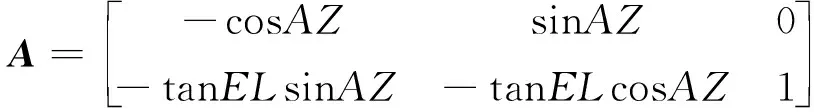
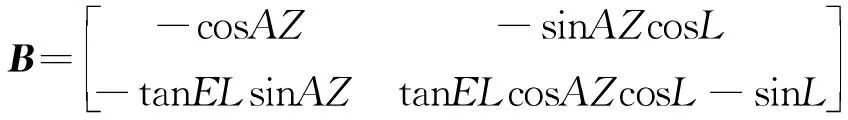
(17)

Δ=-, Δ=-

(18)

Δ、Δ分別為慣性輸出信息等效后的天文觀測角與星敏直接觀測到的觀測角之差；、分別為星敏感器觀測輸出的高度角和方位角的觀測誤差。通過以上建模方法，在保證了原有慣性/天文組合導航系統不受影響的前提下，增加了對安裝誤差的實時估計，并使得安裝誤差對組合導航系統的影響能夠被及時消除。同時系統狀態量的維數僅由18維增長到21維，仿真驗證表明，單次卡爾曼濾波計算時間增長到了原來的1.36倍左右，并未過多地引起計算成本的增加。

式(16)為單星觀測條件下的量測方程，當能觀測到不止1顆導航星時，可以將式(16)進行擴展，即實現基于多星觀測的量測方程，進一步提高安裝誤差估計精度。以2顆導航星為例，在雙星觀測條件下的量測方程為

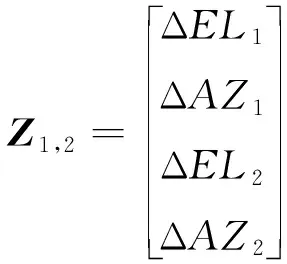
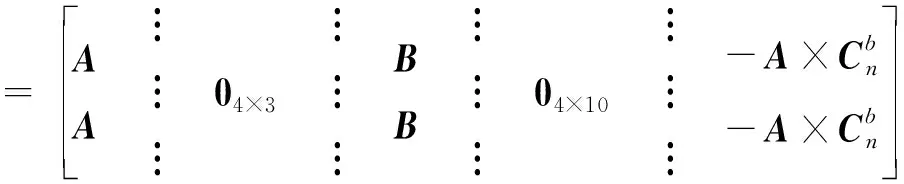
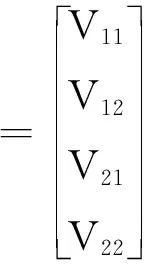
(19)

式中，、、、分別對應2組高度角和方位角的觀測誤差。

4 基于可觀測性分析的誤差標定飛行器航跡設計

系統可觀測性分析方法包括基于奇異值分解的可觀測性分析法和基于特征值的特征向量分析法，文獻[20]對兩種方法的原理和特點進行了詳細分析，文獻[21]針對星敏安裝誤差的估計與飛行器機動方式的關系進行了分析。本文采用奇異值分解的可觀測性分析方法，通過產生不同的航跡飛行模式，對星敏安裝誤差在線辨識的可觀測度進行了詳細分析，并模擬了三種典型的轉動機動方式，如表1所示。

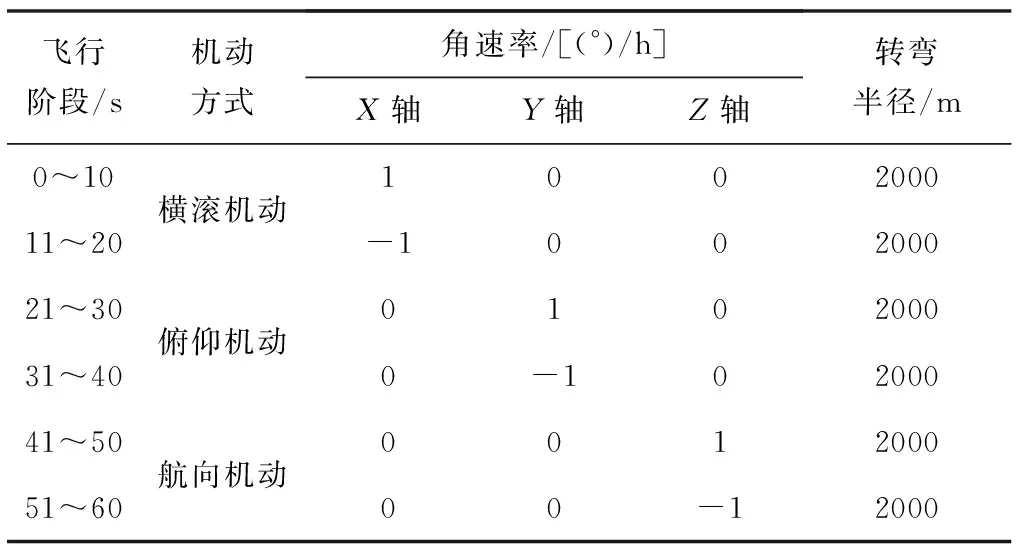
表1 轉動機動方式

繪制不同機動方式下星敏安裝誤差對應的奇異值直方圖,如圖4所示。

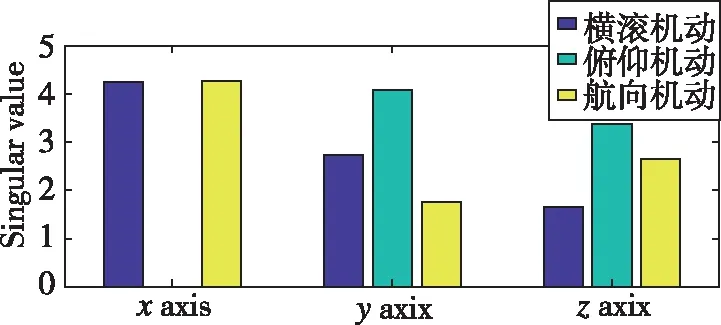
圖4 星敏安裝誤差角對應的奇異值Fig.4 Singular value corresponding to star sensor installation error angle

從圖4中可以看出，沿著機體系軸的安裝誤差在做橫滾機動和航向機動時奇異值較大；俯仰機動對沿著軸的安裝誤差激勵效果比較好;軸的安裝誤差在做俯仰機動時有比較好的可觀測性。

通過圖4所示的可觀測性分析結果可以看出，僅通過機體的橫滾和俯仰機動即可實現沿著機體系3個方向的星敏感器安裝誤差的較好激勵，從而對其進行在線標定。基于空天飛行器跨空天的飛行模式和大動態長航時的任務特性，設計了圖5所示的航跡規劃方案，航跡總時間為1800s，其中前400s為標定階段，包含了載體0～90s的橫滾機動和200～290s的俯仰機動，使得星敏的安裝誤差具有比較好的可觀測性，從而達到實時估計的目的；400～1800s為導航階段，包含了3個軸向的線運動和角運動，對誤差校正的有效性進行了驗證。載體初始位置為東經118°，北緯32°，高度100km，初始北向速度100m/s，初始北向和天向速度為0，初始姿態角均為0。

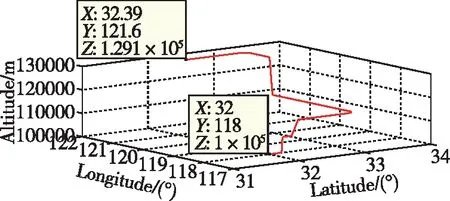
圖5 航跡方案Fig.5 Track plan

5 仿真驗證與結果分析

利用第4節中的航跡對標定方案進行仿真驗證，該標定方案依賴高精度的天文觀測水平基準，水平基準誤差會導致星光矢量觀測的偏移，如圖6所示。同時，慣性/天文組合導航系統的水平基準精度由慣導姿態輸出精度決定，本文通過四種仿真參數配置方案，以3顆觀星條件為例，分析了不同慣導精度條件下的水平基準偏移和星敏安裝誤差標定結果，如表2所示，陀螺噪聲包括白噪聲和一階馬爾可夫過程模擬的有色噪聲，星敏感器觀測噪聲為白噪聲,其中水平基準精度通過慣導姿態誤差角體現。

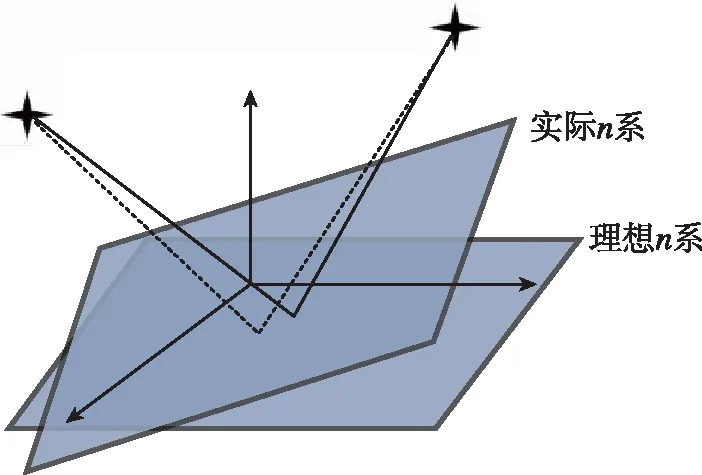
圖6 天文觀測水平基準誤差示意圖Fig.6 Astronomical observation level reference error

將不同條件下的安裝誤差標定結果與表2中設定的安裝誤差參數進行對比分析，結果如圖7和表3、表4所示。

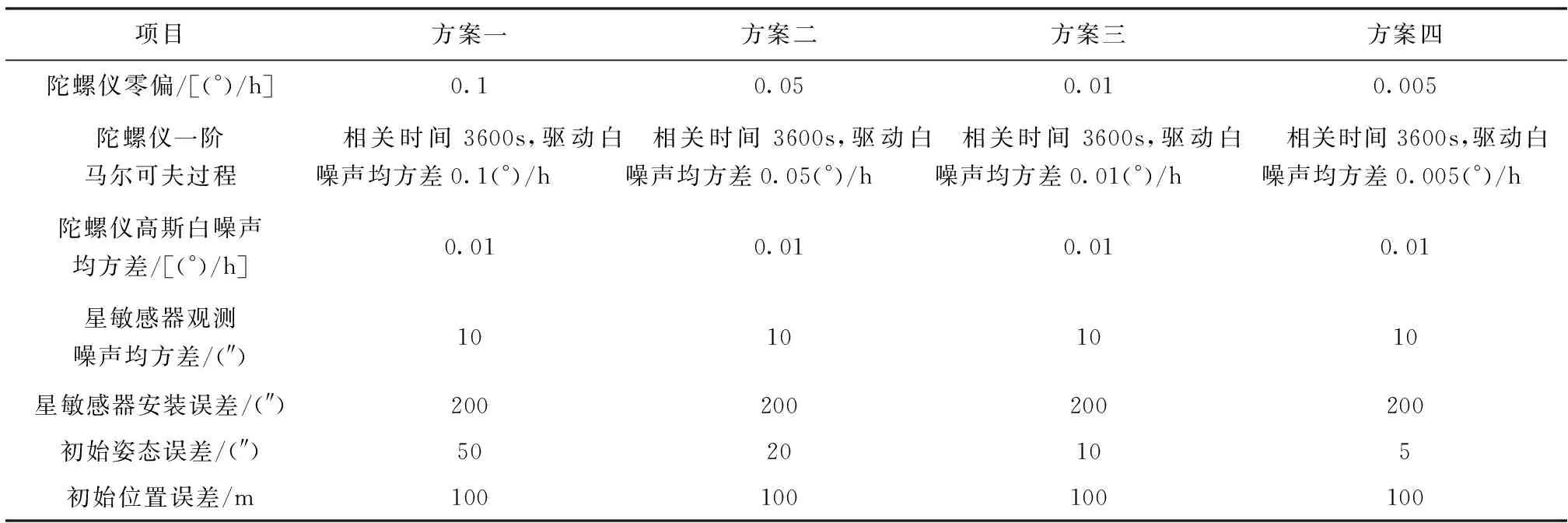
表2 系統誤差參數

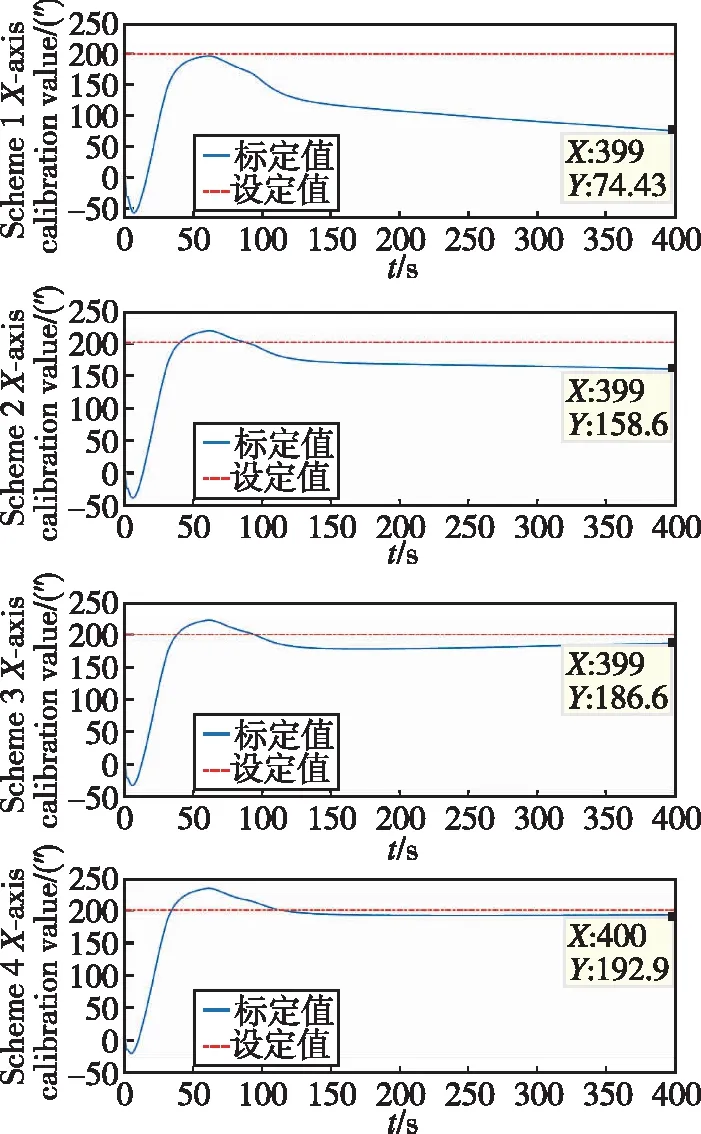
(a) x軸安裝誤差標定曲線

(b) y軸安裝誤差標定曲線

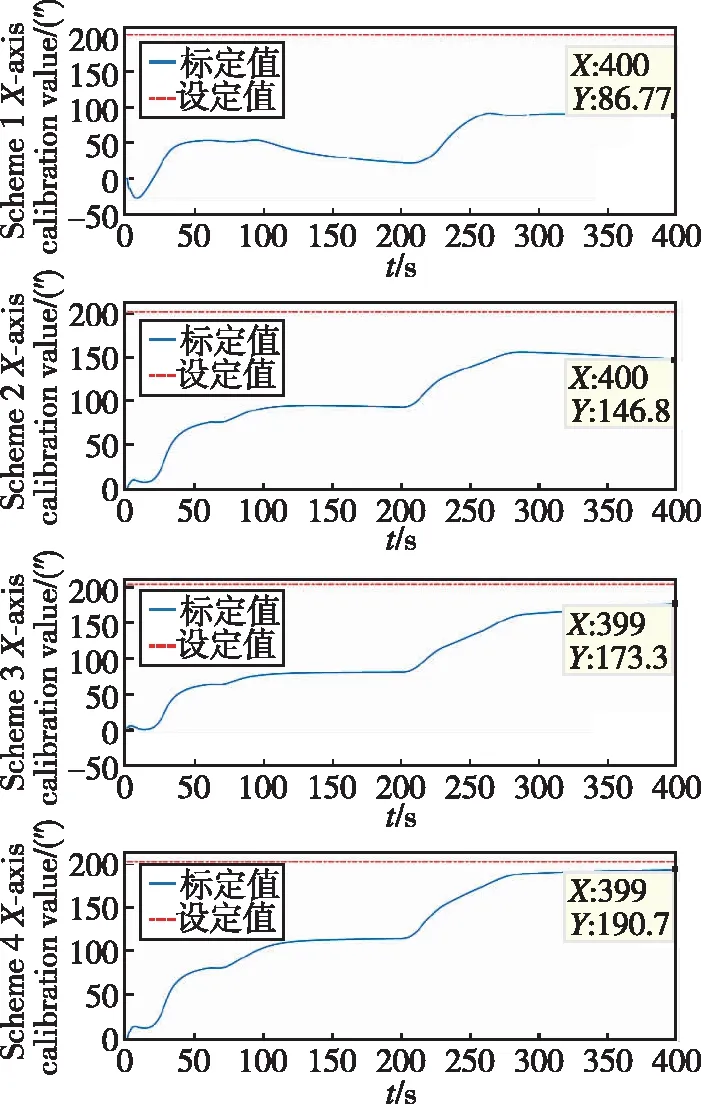
(c) z軸安裝誤差標定曲線圖7 四種條件下星敏安裝誤差標定曲線Fig.7 Star sensor installation error calibration curve under four conditions

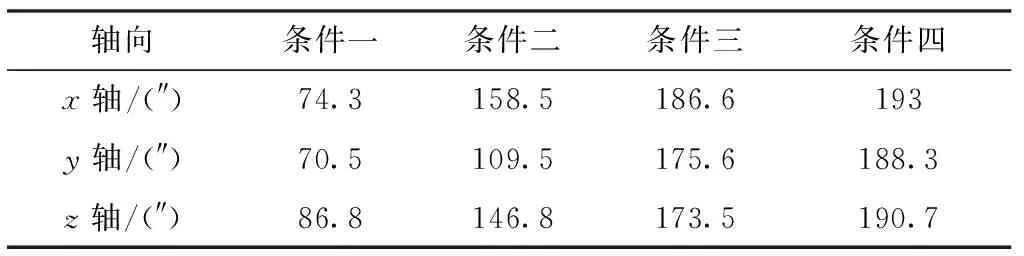
表3 四種條件下星敏安裝誤差標定結果

表4 四種條件下慣導姿態誤差值

通過圖7和表3、表4的結果可以看出，不同精度等級的慣導系統將引起不同精度等級的姿態輸出，同時決定了不同星敏感器觀測的水平基準精度，進而影響星敏感器安裝誤差的估計精度。從方案一和方案二的仿真結果可以看出，精度過低的慣導系統將無法實現對星敏安裝誤差的有效標定；條件三和條件四的標定結果能達到預設誤差85%以上，其中軸能達到90%以上；另外，在橫滾機動的0～90s內，軸方向已實現大部分預設安裝誤差值的估計，在120s后曲線趨于穩定；對于發生橫滾機動的200～290s內，軸和軸方向也基本實現了預設安裝誤差值的估計，并在300s后開始趨于穩定，證明了該算法的收斂速度較快，能夠滿足一定的實時性要求。因此，在保證一定慣導精度的前提下，利用所設計的動態參數辨識方案能夠實現對星敏安裝誤差的有效在線標定。

以方案三慣導精度為例，利用在線安裝誤差標定值對星敏感器進行安裝誤差反饋補償，校正前后的慣性/天文組合導航系統誤差對比如圖8和表5所示。

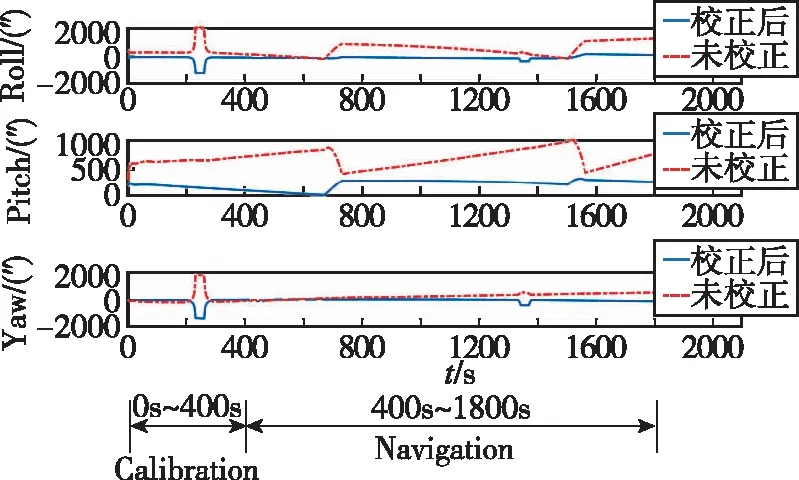
(a) Attitude error

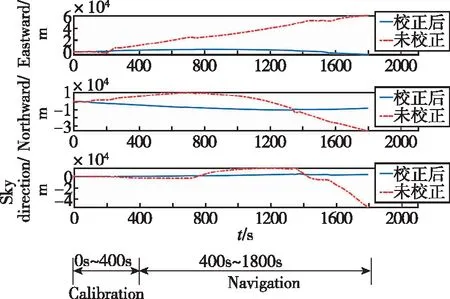
(b) Position error

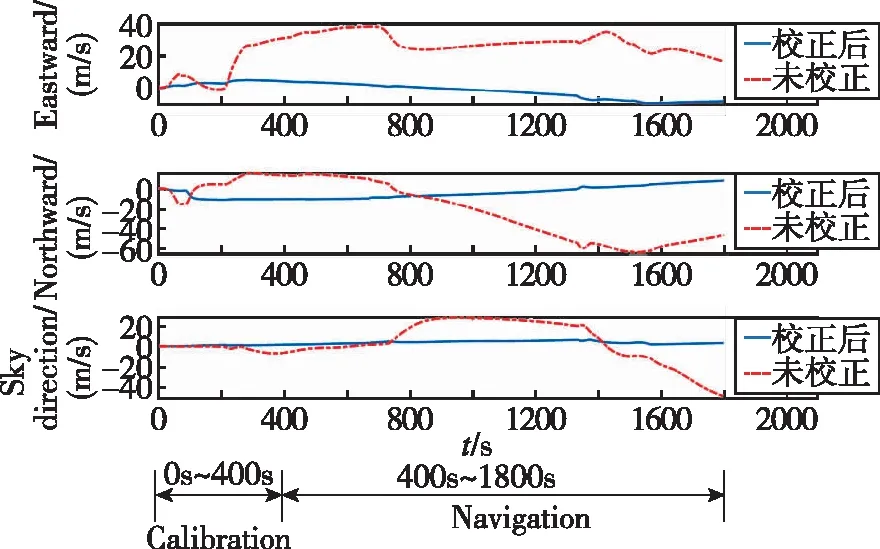
(c) Velocity error圖8 未校正與校正后組合導航系統輸出誤差對比Fig.8 Comparison of output errors of uncorrected and corrected integrated navigation systems

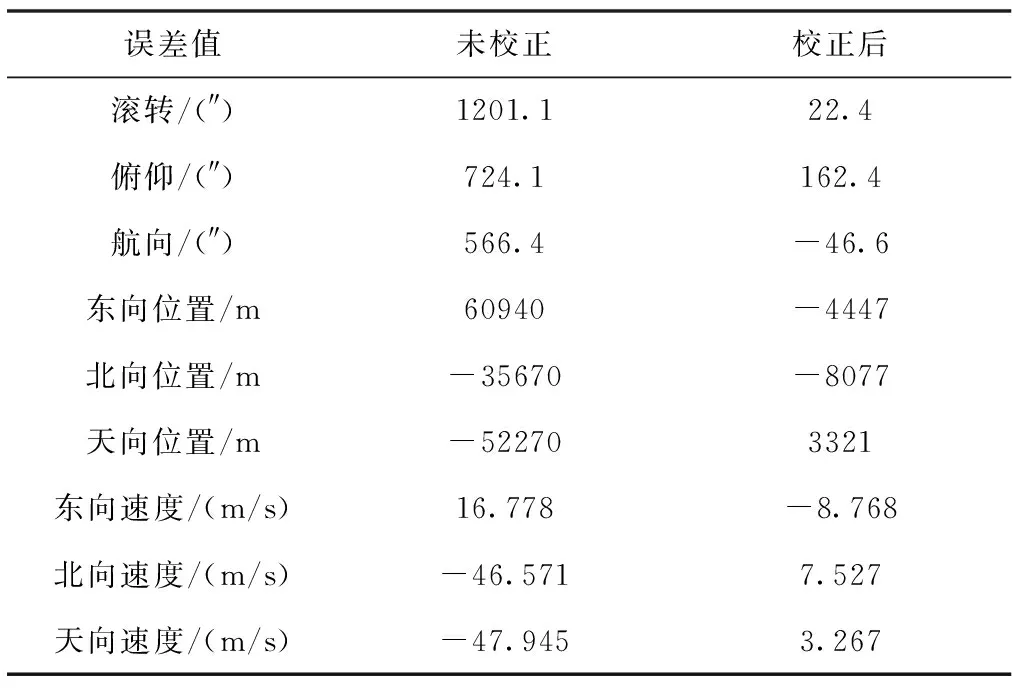
表5 組合導航系統的最終誤差值

由圖8和表5可以看出，采用本文設計的在線標定校正算法的慣性/天文組合導航系統的定姿、定位精度遠高于未校正的慣性/天文組合導航精度，姿態、位置和速度誤差均下降了1個量級，精度提高了10倍，有效減少了星敏安裝誤差對組合導航系統性能的影響，能夠滿足高精度星敏感器補償慣導系統誤差的要求。

6 結論

本文建立了基于高度角和方位角觀測的慣性/天文組合導航的卡爾曼濾波模型，通過模型可以看出，慣導的數學平臺誤差角與星敏感器的安裝誤差角之間存在著耦合關系，建立了通過觀測量估計星敏感器安裝誤差角的濾波模型。

本文設計了星敏安裝誤差動態標定方案，基于構建的誤差標定模型,利用卡爾曼濾波器對星敏安裝誤差進行實時標定。仿真結果顯示，該方案能夠準確且快速地對3個軸向上的安裝誤差進行實時估計，校正后組合導航輸出精度得到了大幅提高，證明了本文提出的星敏安裝誤差實時校正算法能夠明顯地提高慣性/天文組合導航系統輸出結果精度。

在理論分析之外，依然需要結合實際慣導和星敏感器實測數據對所設計的方案算法進行實驗驗證分析，從而實現其工程價值。