洛倫茲對稱破缺框架下的廣義克萊因-戈爾登諧振子*

王恩權 陳浩 楊毅 隆正文? Hassanabadi Hassan

1) (貴州大學物理學院,貴陽 550025)

1 引言

眾所周知,應用于無自旋標量粒子的克萊因-戈爾登(Klein-Gordon,KG)諧振子[1,2]是受狄拉克諧振子[3,4]的啟發而提出的,而狄拉克諧振子是在線性相互作用下描述自旋為1/2 粒子的物理對象.目前,相對論諧振子的推廣,如KG 諧振子[5-10]、Kemmer 諧振子[11]、Duffin-Kemmer-Petiau 諧振子[12-14]以及狄拉克諧振子[15,16]的廣義化是理論物理學家特別感興趣的研究課題,尤其是在拓撲缺陷背景下的諧振子研究吸引了許多物理學家的興趣.文獻[8]在宇宙弦時空中通過一個新的動量算符來替代之前的動量算符實現了KG 諧振子的廣義化,即作這樣一個動量算符的替換:pμ →pμ+imωXμ.

此外,隨著量子力學[17]和相對論的發展,由麥克斯韋電磁學衍生出來的規范理論已逐漸在物理學的各個分支中得到證實,如粒子物理學中弱電相互作用的統一解釋了放射性衰變現象,基于希格斯機制,闡明了粒子物理學中的對稱性和對稱性自發破缺問題,建立了統一除引力之外的所有相互作用的標準模型(standard model,SM).然而,SM 面臨著一些無法解釋的物理現象,如暗物質和暗能量及引力相互作用等,因此,Kosteleck 和Samuel[18]在弦理論的基礎上提出了具有洛倫茲對稱破缺(Lorentz symmetry violation,LSV)的標準模型擴展理論(standard model extension,SME).后來,在考慮有效場論的情況下,具有量子效應的SME 得到了廣泛應用.如Bakke 和Belich[19-21]提出的朗道型量子化理論,他們在LSV 背景下研究了自旋為 1/2 的中性粒子與磁場和電場組成的混合場的相互作用.另外,許多物理學家也在LSV 背景下研究了中性粒子與不同類型的勢函數相互作用的情況,如反平方電勢[22]和庫侖型電勢[23]等.LSV的應用還包括幾何量子相位[24,25]和宇宙弦背景時空[26,27]等領域.

本文主要基于LSV 框架研究KG 方程描述的標量粒子的相對論量子效應.文獻[28]分析了LSV 對KG 方程的影響.Vitória 和Belich[29]研究了KG 諧振子與LSV 產生的線性中心勢的相互作用.因此,我們計劃基于LSV,在存在和不存在磁場兩種情況下研究康奈爾勢函數在洛倫茲對稱破壞框架中對廣義KG 諧振子的影響.本文其他部分的主要內容如下:第2 節簡要回顧LSV,并給出在LSV 背景下具有康奈爾函數的KG 諧振子方程;第3 節分別考慮康奈爾函數在有磁場和無磁場的情況下對KG 諧振子的作用;第4 節是結論.

2 洛倫茲對稱破缺下的廣義KG 諧振子

本節首先介紹洛倫茲對稱破缺框架下的廣義KG 諧振子,從標準模型擴展理論的角度來看,描述存在非最小耦合和電磁張量,且靜止質量為m的相對論標量粒子的KG 方程為(?=c=1)[29]

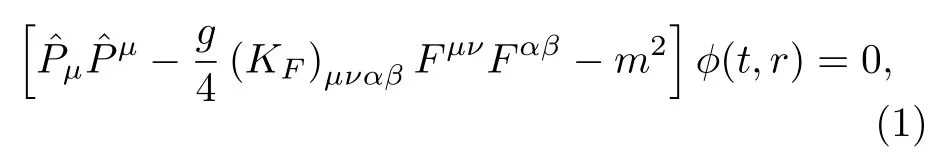
這里的電磁張量Fμν滿足關系Fμν=?μAν -?νAμ,恒定的背景張量場來自于標準模型擴展理論之外的洛倫茲對稱破缺,無量綱的張量系數是具有19 個獨立非零分量的黎曼張量[30].此外張量系數κDE,κDB,κHE和κHB被定義為[31,32]

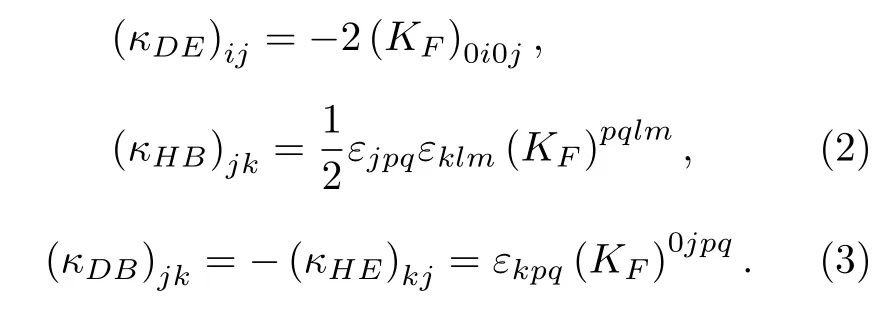
需要強調的是張量 (κDB)jk和 (κHE)kj是反對稱矩陣,(κDE)ij和 (κHB)jk是對稱矩陣.因此協變KG方程被重新表示為

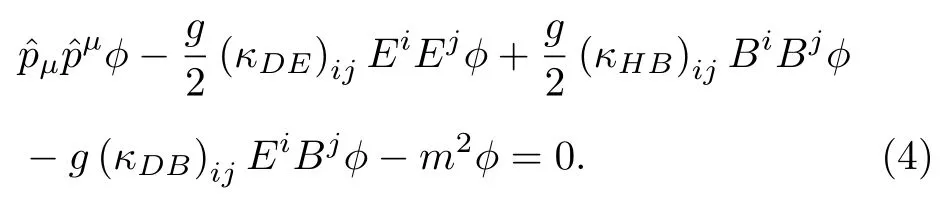
眾所周知,KG 諧振子也被稱為帶有諧振子的KG場[1,2],通過非最小耦合,動量算符的相應變化如下:

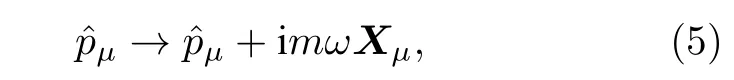
其中ω表示角頻率.基于這一點,本文應用(1+3)維柱坐標形式下的閔可夫斯基時空度規

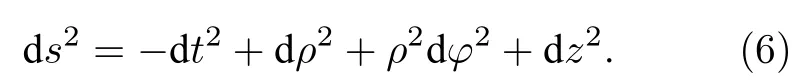
因此在考慮(5)式的作用后,(4)式中的KG 諧振子方程被重新寫為

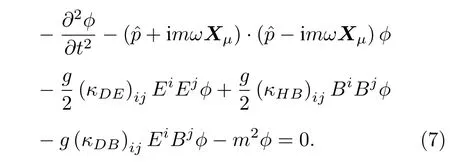
眾所周知,KG 諧振子是通過考慮一個非最小耦合項的向量Xμ=(0,ρ,0,0,0)=ρρ? 得出的,在這種情況下,用徑向勢函數f(ρ) 來代替ρ把KG 諧振子廣義化,也就是

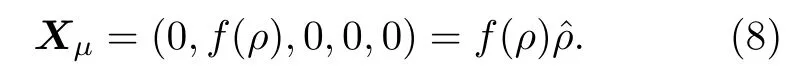
因此把(8)式代入(7)式,就可以得到如下二階微分方程:

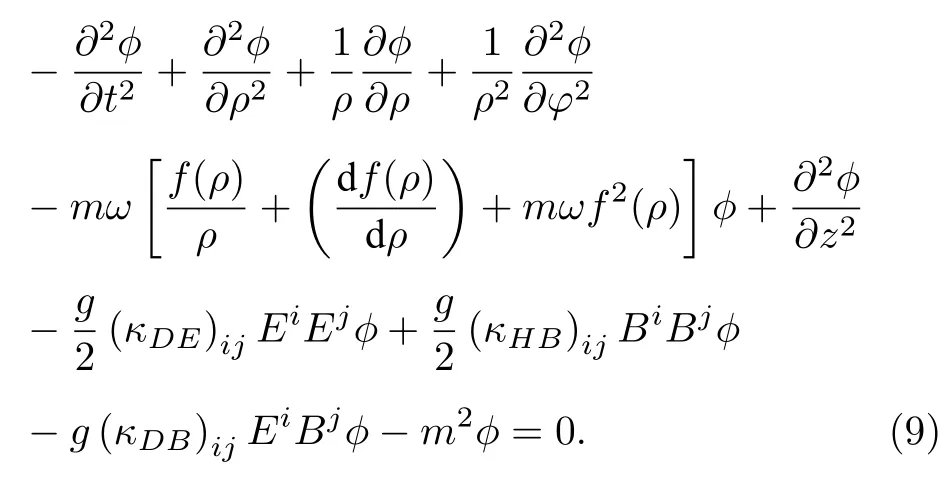
下面研究康奈爾勢函數對廣義KG 諧振子的影響,康奈爾勢函數f(ρ) 可以寫為

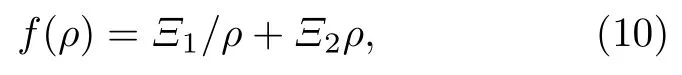
其中參數Ξ1和Ξ2分別表示規范理論中的庫侖強度和弦張力.值得一提的是,康奈爾勢在粒子物理學中有廣泛的應用[33-36],它包含一個描述夸克和膠子相互作用的短程庫侖勢,以及一個長距離線性勢.把(10)式代入(9)式可以得到

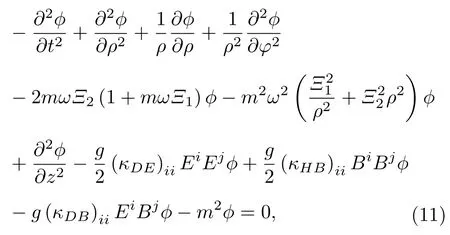
其中動量算符為=-i?z,角動量算符為=-i?φ.假設方程(11)的特解為

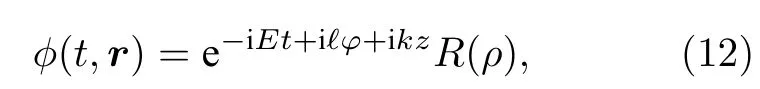
我們知道,徑向波函數獨立于坐標系的其他分量t,φ和z,(12)式中的?=0,±1,±2,···是角動量算符的特征值,k是線性動量算符在z分量的特征值.

此時,把(12)式代入(11)式中得到

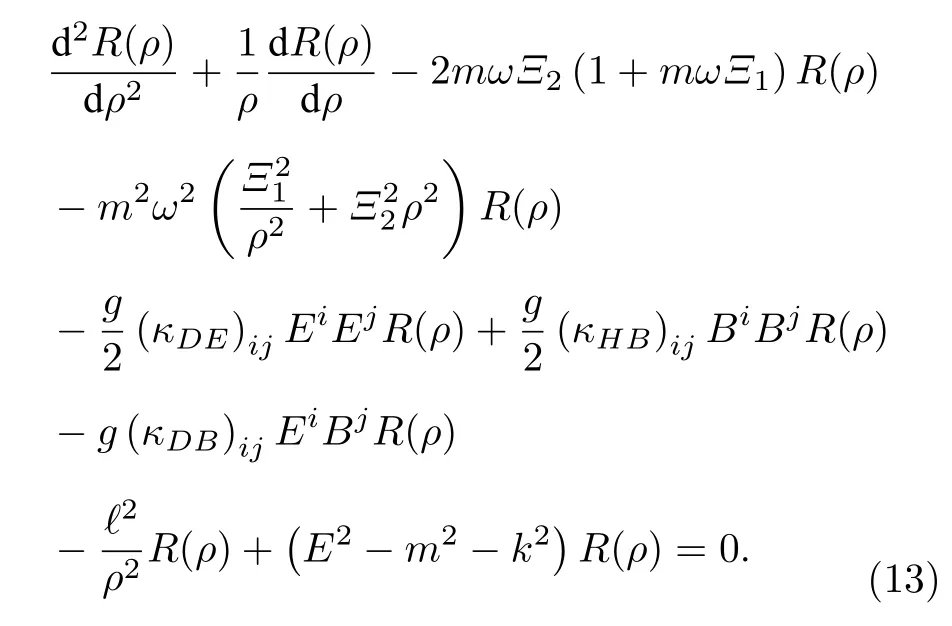
第3 節將研究在存在康奈爾勢情況下洛倫茲對稱破缺對廣義KG 諧振子的影響.

3 洛倫茲對稱破缺下廣義KG 諧振子的能級與波函數

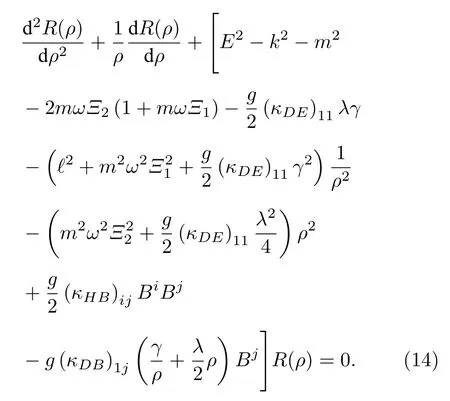
現在來求解方程(14)在兩種不同情況下的能量本征值與束縛態波函數.

情況一不存在磁場,即B=0,此時待求解的方程(14)可被重新寫為

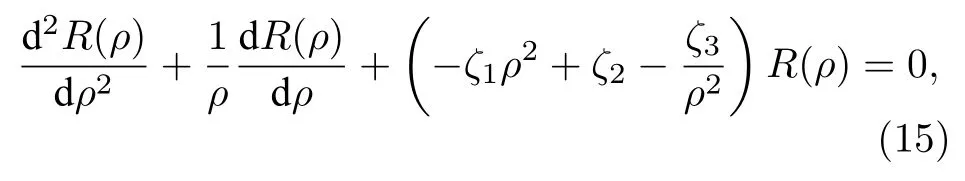
其中

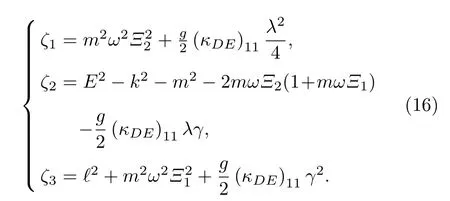
為了求解方程(15),令r=ρ2,則方程(15)變為

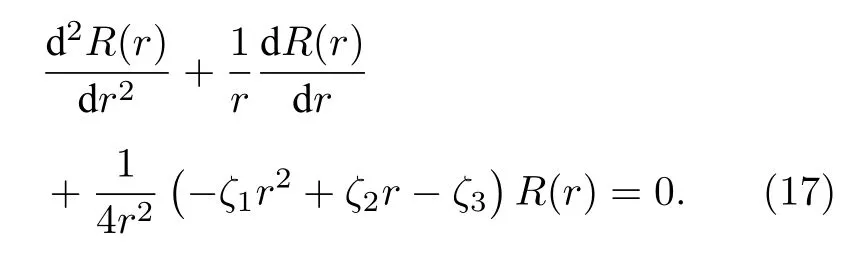
此時,可以發現波動方程與NU 方法[41,42]中的方程形式類似,Nikiforov-Uvarov (NU)方法對于求解量子理論中波動方程束縛態的精確解是非常有用的[43-48],NU 方法的詳細說明見附錄A.根據文獻[48]結果,再依據附錄A 中的NU 方法,可以得到波函數

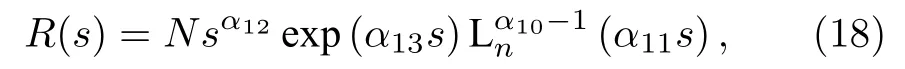
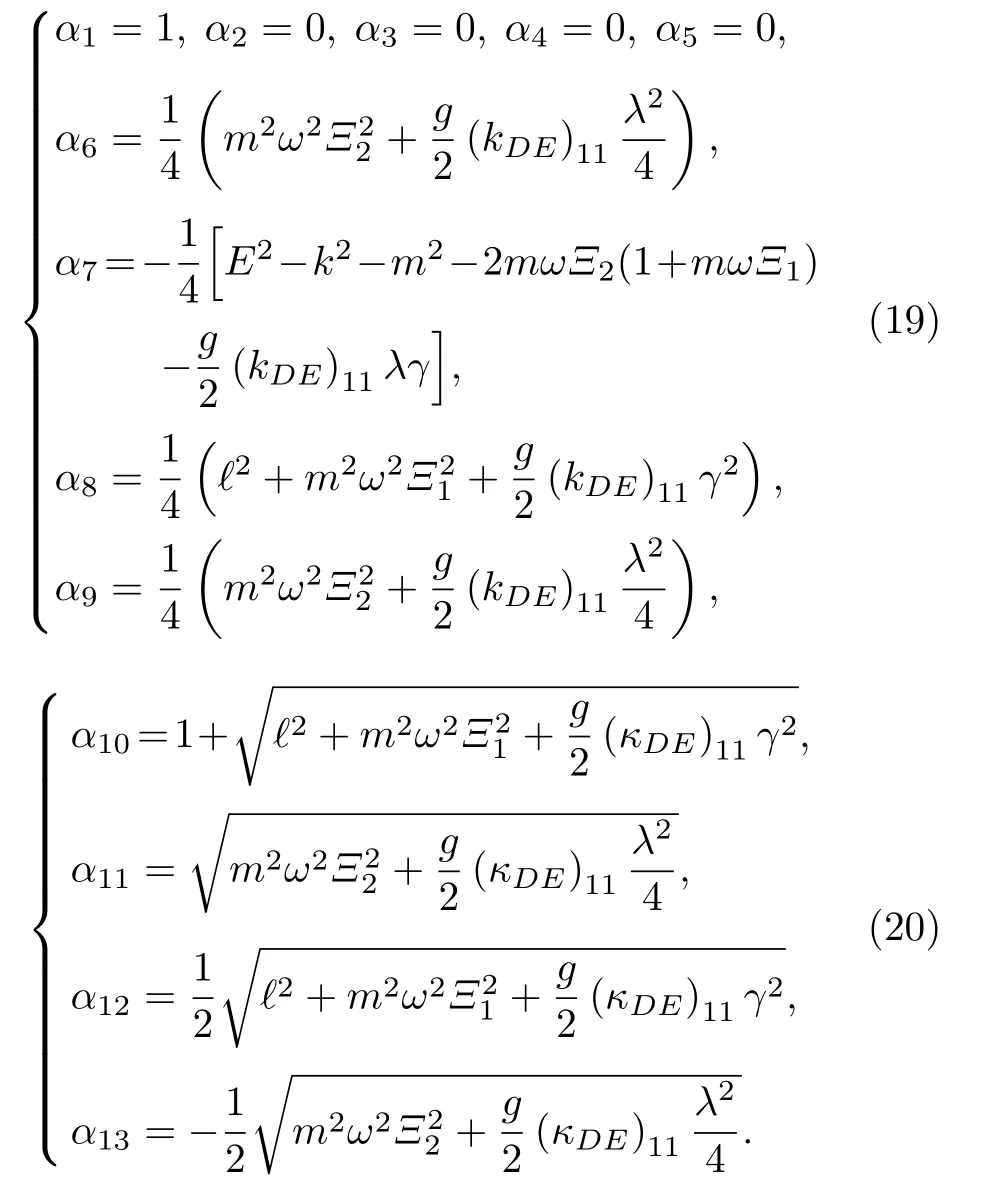
將(19)式和(20)式代入(15)式,得到無磁場時洛倫茲對稱破缺下KG 諧振子的非歸一化徑向波函數為

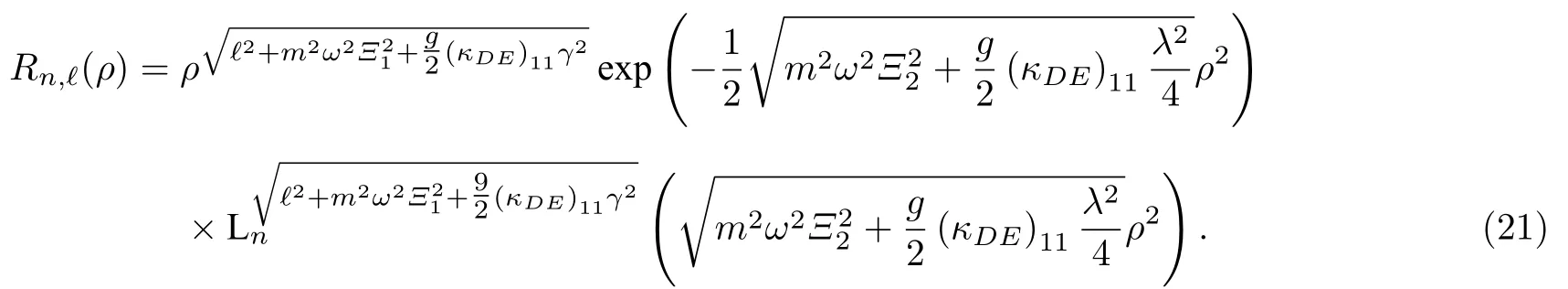
此外,為了更直觀地反映不同λ值對波函數的影響,圖1 給出了徑向波函數R(ρ) 的圖像.可以看出,在ρ →0 時徑向波函數R(ρ) 的值為零,另外,徑向波函數的振幅隨著電場強度的增加而減少.通過系數關系

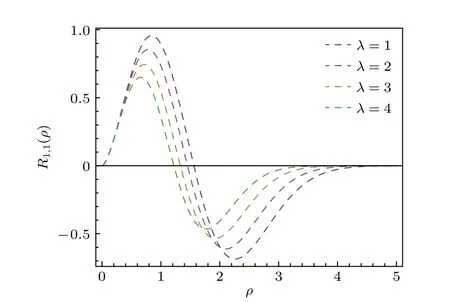
圖1 以 ρ 為變量取4 個不同 λ 值的徑向波函數Fig.1.Radial wave functions as a function of ρ for different λ .

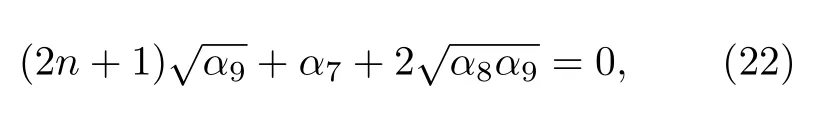
得到能量特征值為

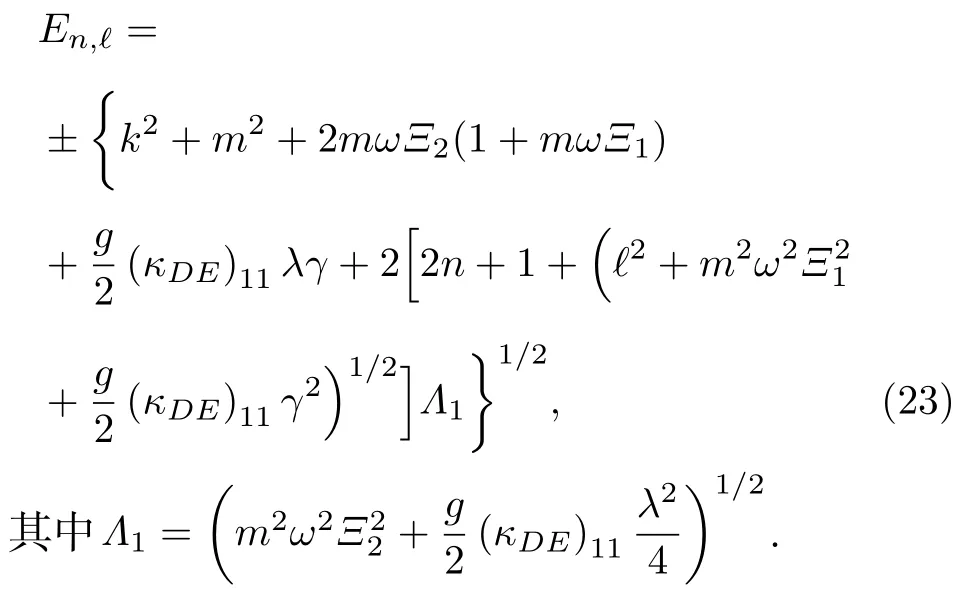
如果康奈爾勢函數參數滿足Ξ1=0,Ξ2=1,可以得到線性勢作用下KG 諧振子的能量特征值為

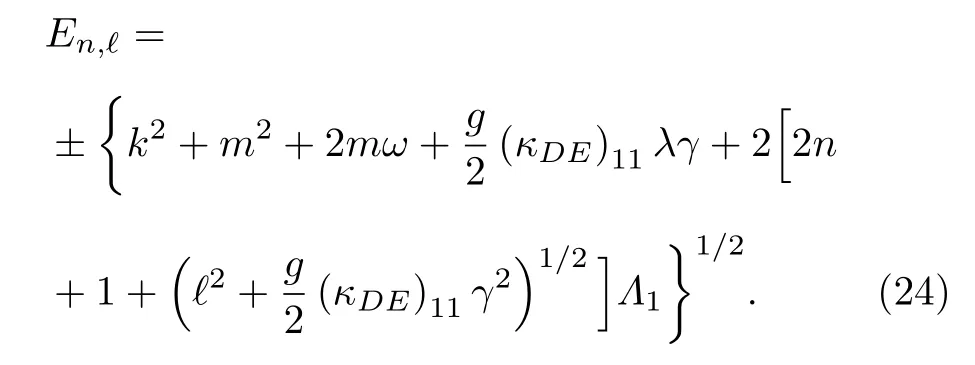
情況二 求解存在磁場B=B0的情況.方程(14)可重新寫為

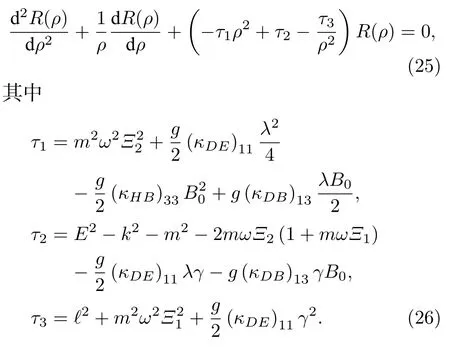
為了得到一個可解的波函數,令η=ρ2,則有

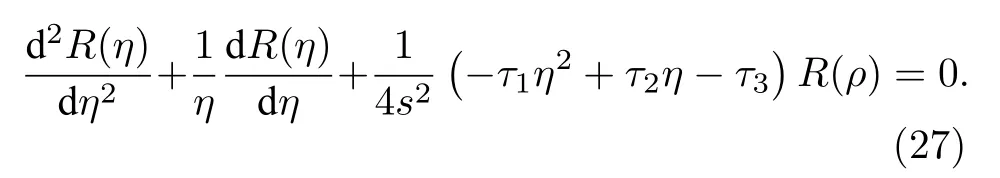
不難發現,方程(27)與NU 方程形式類似,所以同樣利用NU 方法來處理這種情況.因此方程(27)的波函數可以假定為

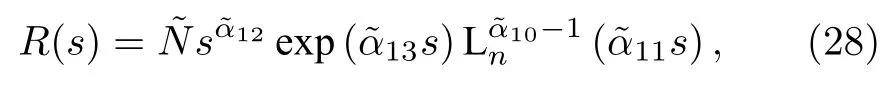
相關系數表示為

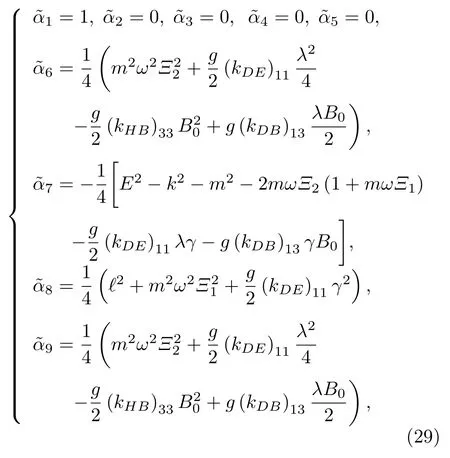
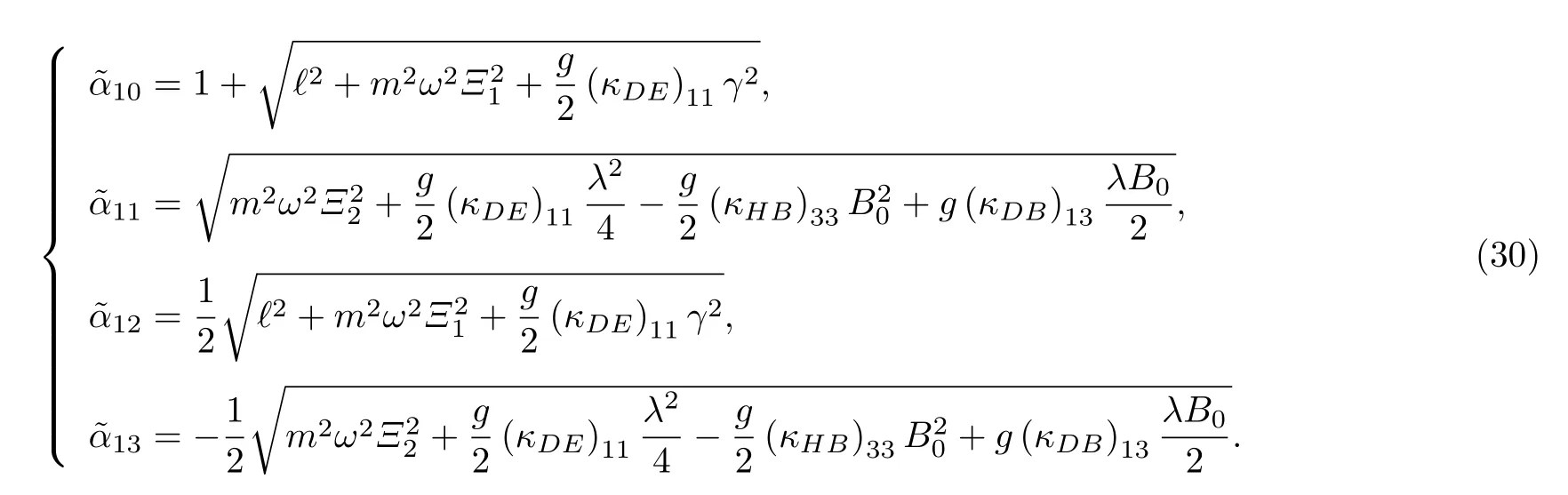
在洛倫茲對稱破缺中具有康奈爾勢函數且存在磁場情況下的廣義KG 諧振子的非歸一化徑向波函數可以寫為

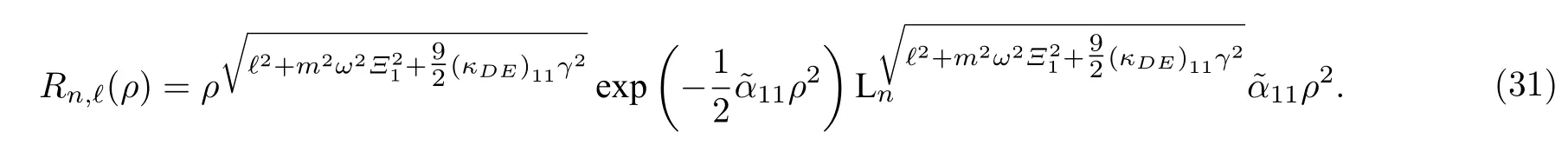
波函數(31)明顯依賴于量子數l及圖2 為非歸一化的徑向波函數R(ρ) 的圖像,在圖2中,令=(kDB)13=1,把ρ作為橫坐標,畫出了廣義KG 諧振子在不同Ξ1值時的圖像,能清晰地觀察到徑向波函數的振幅隨著勢函數參數的增加而增加.

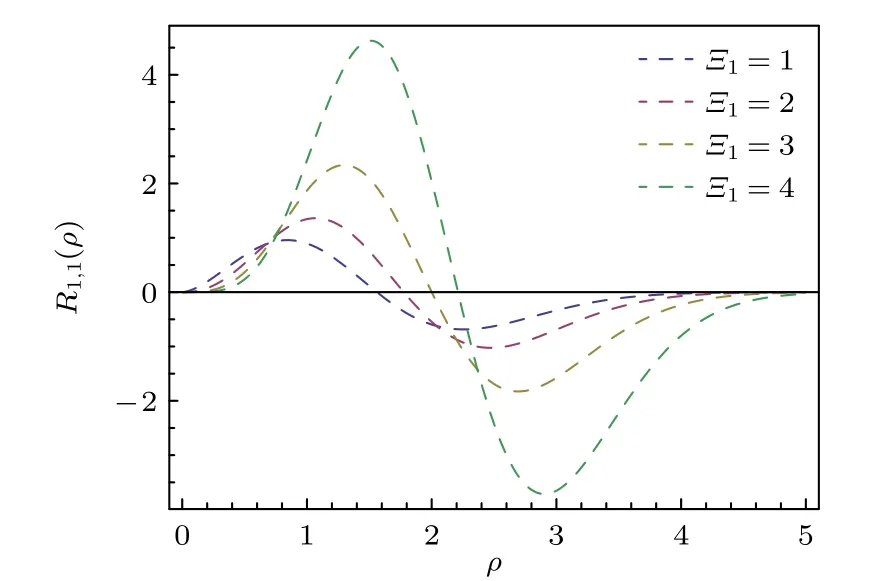
圖2 以 ρ 為變量取4 個不同1 值的徑向波函數Fig.2.Radial wave functions as a function of ρ for different 1 .

根據系數關系

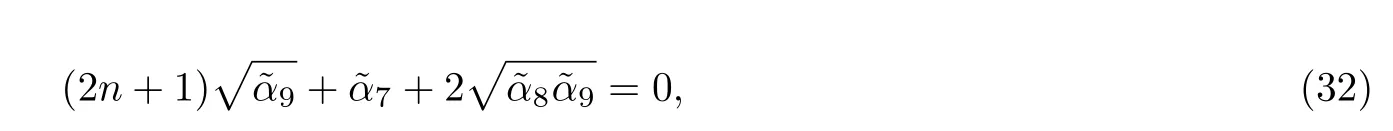
相應的能量特征值為

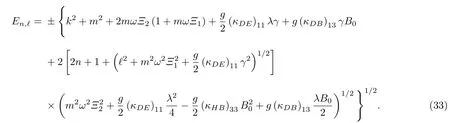
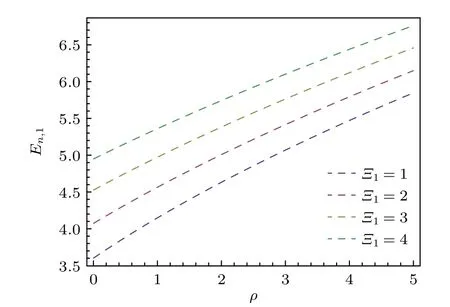
圖3 以n 為變量取個不同 1 值的能量Fig.3.Energy eigenvalue as a function of n for different 1 .

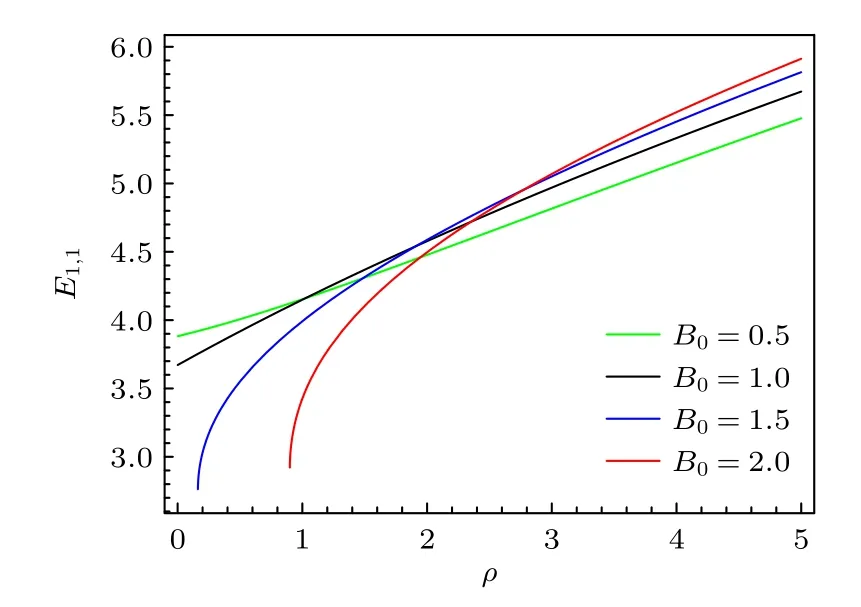
圖4 以 λ 為 變量取4 個不同 B0 值的能量Fig.4.Energy eigenvalue as a function of λ for different B0 .

4 總結

本文研究了洛倫茲對稱破缺框架下的廣義KG諧振子,利用NU 方法分析了存在與不存在磁場時的廣義KG 諧振子.此外還討論了KG 諧振子在1的特殊情況.結果表明,存在磁場時的情況是無磁場情況的推廣,因為當令B0=0時,束縛態能量特征值與無磁場時所得結果一致.兩種情況下的徑向波函數明顯取決于洛倫茲對稱破缺效應相關的參數和康奈爾勢參數.此外,通過固定一些參數值,可以觀察到在ρ→0 時徑向波函數R(ρ) 的值也為零.另外,根據本文所畫的圖像得知,圖1 中的徑向波函數的振幅隨電場強度的增加而減少,而圖2 中的徑向波函數的振幅隨勢參數的增加而增加.圖3 顯示了勢函數參數對廣義KG 諧振子能譜的貢獻.可以看出,當固定量子數n時,較大的勢函數參數對應著較大的能量特征值,而當固定勢函數參數時,較大的量子數n所對應的能量特征值也相對較大.最后,發現在圖4 中的能量特征值存在簡并,同時在B0=1.5 和2 時,λ較小時能量特征值的增加趨勢尤為顯著.此外,從能譜的圖像可以清晰地看到洛倫茲對稱破缺的存在使得能譜得到了修正.

附錄A Nikiforov-Uvarov 方法

本文利用NU 方法求解了二階微分方程的本征函數,該方法有助于找到各種類薛定諤方程的特征值和特征函數,也可以用于一些涉及到二階微分方程的其他物理背景中.在NU 方法中微分方程通常可以寫成如下形式:

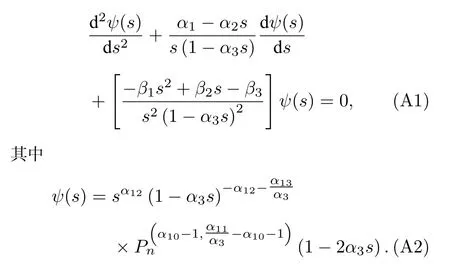
在NU 方法中微分方程的本征值通常通過如下方程給出:

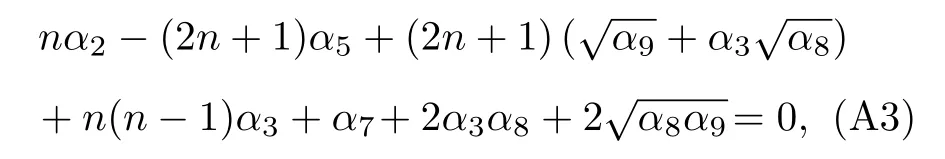
其中涉及到的所有參數(α4···α13)都是通過α1,α2,α3和β1,β2,β3這6 個參數得到的:

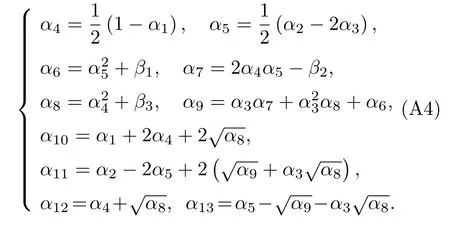
而α1,α2,α3和β1,β2,β3這6 個參數的值是可以通過微分方程(A1)直接確定的.

另外,對于α3=0 這種特殊情況有如下關系:

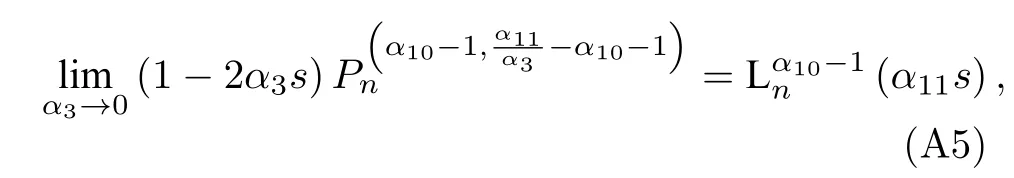
此時的波函數為