基于最短路徑長度的空間網絡路由*

林泓 夏永祥? 蔣路茸

1) (杭州電子科技大學通信工程學院,杭州 310018)

2) (浙江理工大學信息學院,杭州 310018)

1 引言

20 世紀50 年代末,Erd?s 與Rényi[1]提出的ER 隨機圖模型開辟了復雜網絡領域研究的先河.直至20 世紀末,小世界網絡[2]的提出與無標度特性[3]的發現,吸引了一大批科學家參與到復雜網絡結構與動力學的研究之中.近十年來,復雜網絡成為生物技術、移動通信、交通運輸、社會關系等多個不同領域的研究熱點[4-8],受到物理、數學、計算機、通信、社會學等領域學者的廣泛關注.實際生活中的Internet、移動通信網絡、交通運輸網絡、電力網等都可以被抽象成復雜網絡進行研究分析,而這類網絡的傳輸性能與人們的生活息息相關.如何提升網絡的傳輸性能已經成為復雜網絡領域研究的熱門課題之一.網絡傳輸能力主要取決于網絡的拓撲結構與路由方式,針對這兩方面的影響因素,一般有“硬策略”和“軟策略”兩種優化方式[9],即優化網絡拓撲結構與優化路由方式.而在實際生活中,不少網絡的結構已經固定,修改其結構需要承擔高昂的成本.因此,采用更加高效的路由策略來提升網絡傳輸性能更具有可行性.

傳統意義上的最短路徑的策略是目前應用較為廣泛的一種路由方式,即負載從節點A通過最少的邊數傳輸到節點B,但是這種方式很容易在一些度值較大的節點處造成擁塞現象[10].因此,不少研究人員提出了更加高效的路由策略[10-20].Yan等[18]提出了一種“the efficient path”的路由策略,定義任意兩點i和j之間的路徑為L(P(i →j):β)=以 m in(L) 為目標選擇路徑,通過繞 開度值較大的節點來減少發生擁塞的可能,大大提升網絡的傳輸性能.Huang 和Chow[19]提出了一種帶記憶信息的路由策略,節點記錄負載的傳輸來源,避免出現回溯現象,使得負載在兩個不同節點之間來回傳輸的機會大大減少,有效地提高網絡吞吐量.Wang 等[20]提出了一種流量模型,負載從節點a傳輸到節點b,若節點a與b之間有邊連接,則負載可直接傳輸至目標節點b;否則,將以Πi=的概率傳輸至a的某個鄰居節點i.

之前提出的各種路由策略主要是基于復雜網絡的拓撲,很少有研究考慮節點的空間位置.而事實上,由于空間網絡中的節點與節點之間的連接受到實際位置的約束,與一般的復雜網絡在拓撲結構和魯棒性[21]等方面具有一定的差異性.在實際生活中,如航空網絡[22]、交通網絡[23]、無線傳感器網絡[24]、無人機網絡[25]等都受到空間位置的限制.由于這類空間網絡的特殊性,對其路由策略的研究具有很強的理論價值和現實意義.

本文提出一種基于最短路徑長度的空間路由方式,即負載從源節點沿著最短路徑長度的方向傳輸到目標節點.Zhao 等[26]在2005 年發表的文章中指出,不同結構的網絡出現擁塞現象的性能不相同.因此,本文考慮了空間勻質網絡和異質網絡兩種情況,在隨機幾何圖[27]和LAEE (local-area and energy-efficient evolution)模型[28]上進行了仿真模擬.仿真結果表明,本文提出的路由策略能夠有效提升網絡的傳輸性能,減少擁塞現象的發生.

2 空間網絡模型

2.1 LAEE 演化模型

研究發現,很多實際網絡都遵循節點的度值呈冪律分布的無標度特性,即P(k)∝k-γ,其中k表示節點的度,γ為常數.為了探究本文提出的路由算法在異質網絡上的適用性,采用Jiang 等[28]提出的具有無標度特性的空間LAEE 演化模型.

該網絡的拓撲演化主要分為兩個階段.在第1 階段,將N個節點隨機分布在1 × 1 的區域S內,每個節點傳輸和處理負載的能力都是相同的.此時所有節點都是孤立的,假設以節點i為圓心、r為半徑的連通區域內所有節點為節點i的潛在鄰居,并定義最靠近原點O的節點為匯聚節點.

在第2 階段,從匯聚節點開始進行網絡的拓撲演化.

步驟1令匯聚節點與其通信半徑r內的a0個潛在鄰居節點進行連接,形成初始網絡T0.

步驟 2在時間步i,定義網絡Ti中具有最多孤立的潛在鄰居的節點為v,在其潛在鄰居中挑選一個節點ni加入到網絡Ti中.

步驟 3如圖1 所示,基于優先連接的原則下,以Πi的連接概率選取網絡Ti中a個節點與節點ni進行連接,并滿足a個節點均在節點ni的連通范圍內;若可選取的節點數小于a,則全部連接.連接概率Πi可通過下式求得:

其中,局部區域指以節點ni為圓心;r為半徑的連通范圍;kmax是默認節點最大的度值;q是已經達到kmax的節點的個數;f(Ei) 是功能函數,為了方便處理,這里取f(Ei)=1 .

步驟 4重復步驟2 和步驟 3,直至區域S內的所有節點都被加入到網絡中.

從上述過程可以看出,在此模型中,雖然N個節點的位置開始就已經確定了,但它們是一個一個加入到網絡中的,且它們的連邊是基于優先連接的原則建立的,因此有少部分節點擁有大量的連接,而大多數節點的度則比較小.LAEE 網絡的度分布如圖2 所示.可以發現其度分布呈現冪律分布的特點,是典型的異質網絡.

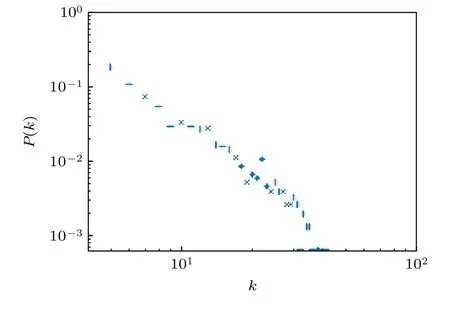
圖2 N=1500,〈 k〉 =8 時的LAEE 網絡的度分布Fig.2.Degree distribution of the LAEE network.N =1500,〈k〉=8.

2.2 隨機幾何圖模型

最簡單的空間網絡是隨機幾何圖模型[24].該模型主要分為以下3 個階段:

步驟1將N個節點隨機地分布在1 × 1 的區域S內.

步驟2 隨機選取一個節點i,以它為圓心,r為連通半徑,構成一個圓形的連通區域.如圖3所示,節點i與其連通區域內的全部節點建立連接.

圖3 節點i 與其連通區域內的全部節點建立連接Fig.3.Node i connects all nodes in its connection area.

步驟3 重復步驟2,直至所有節點都與其連通半徑內的所有節點建立連接.

2.3 改進的隨機幾何圖模型

在節點數N與平均度〈k〉相同的情況下,隨機幾何圖模型的連通半徑要小于LAEE 演化模型.為了更公平地比較勻質與異質網絡,我們希望兩個網絡模型中的連通半徑r相同.對此,本文在經典的隨機幾何圖模型基礎上,提出一種改進的隨機幾何圖模型.

網絡的生成如下所示:

步驟1將N個節點隨機的分布在 1×1 的區域S內.

步驟2隨機選取一個節點i,以節點i為圓心,r為連通半徑,構成一個圓形的連通區域.如圖4 所示,定義連接概率p,節點i與其連通區域內的節點以p概率建立連接.

圖4 節點i 與其連通范圍內的節點以p 概率進行連接Fig.4.Node i connects nodes within its connection range with probability p.

步驟3重復步驟2,直至所有節點都被遍歷到.

從上述過程可以看出,在改進的隨機幾何圖模型中,每個節點的連接概率相同,不同節點之間不存在明顯的差異.該模型的度分布情況如圖5 所示.與LAEE 網絡相比,改進的隨機幾何圖更接近勻質網絡.

圖5 N=1500,〈 k〉 =8 時改進的隨機幾何圖的度分布Fig.5.Degree distribution of the improved random geometric graph.N=1500,〈 k〉=8.

3 路由策略

假設每個節點都具有相同的傳輸負載的能力.負載在網絡上的傳輸過程描述如下:在每一個時間步,網絡產生R個單位的負載,它們的源節點與目標節點均隨機確定,根據路由策略由源節點向目的節點傳輸.每個節點在每個時間步中所能處理的最大負載量為C個單位的負載,為了便于問題的分析,假設C=1 .在每個時間步,負載只能向前傳輸一步,即從一個節點抵達至其鄰居節點.當負載到達目標節點時,自動從網絡中刪除.用參數H(R)表示網絡的序參量[18]:

其中,ΔW=W(t+Δt)-W(t),Δt表示一個時間步的長度,W(t) 表示t時刻網絡中負載的總量.當R較小時,所有的負載都能被及時處理,因此H(R)=0,這種狀態稱為自由流狀態.如果R逐漸增大,使得在某個節點處每個時間步需要處理的負載量超過C,那么必然會有一部分負載無法被及時處理,此時H(R)＞0,即網絡出現擁塞現象.我們關心網絡從自由流狀態到擁塞狀態的相變點處的R值,稱為Rc,它表示網絡在不出現擁塞現象時最多能處理的負載量,即網絡的最大吞吐量.Rc的值一方面取決于網絡的拓撲結構,不同拓撲結構的網絡具有不同的Rc;另一方面,Rc的值取決于所采用的路由方式.因此,本文將在具有不同拓撲結構的空間網絡模型下進行仿真,并對比本文提出的路由方式與傳統的最少跳數路由方式.

3.1 傳統的最少跳數路由策略

在考慮負載傳輸時,經常采用所謂的最短路徑路由.在一般的復雜網絡中,兩點之間的最短路徑通常指它們之間經過最少連邊的路徑,即最少跳數路由.但是,在空間網絡中,所謂最短路徑可能有多種含義,例如跳數最少或者長度最短.為了不引起混淆,本文將通常意義下的最短路徑路由稱為“最少跳數路由”.

在采用最少跳數路由的情況下,可以用介數來描述各個節點的負載情況,任意一個節點v的介數表示如下[18]:

其中σst表示節點s到節點t的最少跳數路徑的數量,σst(v) 表示節點s到節點t的最少跳數路徑中經過節點v的數量.當R＜Rc時,網絡處于自由流狀態,不會出現擁塞現象,單位時間到達節點v的負載為Rg(v)/[N(N -1)] ;當R＞Rc時,網絡出現擁塞現象,假設在節點v處出現擁塞,此時Rg(v)/[N(N -1)]＞C.研究表明,擁塞最先發生在介數值最大的節點處.因此,Rc可表示為[18]

3.2 最短路徑長度路由策略

在空間網絡中,由于每個節點都有一個空間位置,因此每條連邊都有長度.簡單起見,考慮二維平面上的網絡,那么對于連接節點i和j的連邊,其長度為

其中 (xi,yi) 與 (xj,yj) 分別為節點i和j的二維坐標.這樣,對于任意節點對 (s,t),可以定義它們之間的一條路徑的長度為這條路徑所經過的所有連邊長度之和.即路徑

的長度為

在這些路徑中,長度最小的路徑被稱為最短長度路徑,而其長度被稱為最短路徑長度,采用最短長度路徑的路由策略稱為最短路徑長度路由.可以看到,這種路由策略只可能出現在空間網絡中,因為連邊長度乃至路徑長度的概念是建立在節點的空間坐標基礎上的.

需要說明的是,采用最短路徑長度路由策略時,節點的介數仍可以采用類似(3)式的方法計算,但是式中的變量含義有所變化.具體地,σst表示節點s到節點t的具有最短長度的路徑的數量,σst(v)表示節點s到節點t的具有最短長度的路徑中經過節點v的數量.

4 路由性能仿真及分析

為了檢驗兩種路由策略的性能,采用前文提到的LAEE 演化模型和改進的隨機幾何圖模型兩種空間網絡進行仿真實驗.其中,LAEE 演化模型產生具有無標度特性的空間網絡,是典型的異質網絡;而改進的隨機幾何圖模型繼承了經典隨機幾何圖模型的特點,是典型的勻質網絡.

先將N個節點隨機地分布在1 × 1 的區域S內,由于空間位置的限制,節點i只能與以節點i為圓心,r為半徑的區域內的潛在鄰居節點進行連接.根據(5)式,可以計算出任意兩點之間的距離,找到節點i的所有潛在鄰居節點,再根據LAEE與改進的隨機幾何圖模型的生成規則,將節點i與其部分潛在鄰居節點連接,分別生成具有異質與勻質特性的空間網絡.

對于網絡的任意節點對,其路徑可由(6)式來表示.在空間網絡的背景下,連邊被賦予了長度的屬性,通過(7)式可以得到任意節點對之間的路徑的長度,本文提出的最短路徑長度的路由正是基于(5)式—(7)式去尋找任意節點對 (s,t) 之間的最短長度的路徑,即 m inL(s →t) .傳統的最少跳數路由和最短路徑長度路由從不同角度刻畫了節點之間的“最短路徑”.接下來將通過仿真分析來比較兩種路由的性能,進而確定那種路由效果更好.

首先對兩種路由策略下的拓撲指標進行分析.不同路由策略下平均路徑長度、平均跳數與節點數N的關系如圖6 和圖7 所示.可以看到,正如它們的名稱所示,最少跳數路由具有更小的平均跳數,而最短路徑長度路由具有更小的平均路徑長度.比較兩種網絡可以發現,結構上異質的LAEE網絡具有更短的平均路徑長度和更小的平均跳數.這是因為LAEE 網絡中具有少量大度節點,它們提供了傳輸的捷徑.但是,在同一種網絡中,隨著節點數的增加,平均路徑長度略有減少,而平均跳數卻有所增加.這是因為在保證平均度不變的前提下,隨著節點數的增加,連通半徑r是不斷減小的.這樣,平均來講,從源節點到目的節點所經過的連邊數會增加.

圖6 平均度 〈 k〉=4 時,不同節點規模下兩種路由方式平均路徑長度的比較 (a) LAEE 演化模型;(b)改進的隨機幾何圖模型.圖中每個點是10 次仿真的平均值Fig.6.With the average degree 〈 k〉=4,the average path length under two routing strategies with different node sizes:(a) LAEE evolution model;(b) improved random geometric graph model.Each point is the average of 10 runs.

網絡最大吞吐量Rc與節點數N的關系如圖8所示.可以看出,無論在哪種網絡中,最短路徑長度路由都具有更大的Rc值,這說明采用最短路徑長度路由會有效提高空間網絡的吞吐量.當然,如圖7 所示,最短路徑長度路由增加了平均跳數,這將導致平均傳輸延時變長.也就是說,最短路徑長度路由提高空間網絡吞吐量是以增加傳輸延時為代價的.而比較兩種網絡發現,結構上異質的LAEE 網絡具有更小的Rc值,這是因為異質網絡中的大度節點在提供傳輸捷徑的同時,不可避免地成為傳輸的瓶頸,制約了網絡的吞吐量.此外,網絡吞吐量隨著網絡規模增加而增大.

圖7 平均度 〈 k〉=4 時,不同節點規模下兩種路由方式平均跳數的比較 (a) LAEE 演化模型;(b)改進的隨機幾何圖模型.圖中每個點是10 次仿真的平均值Fig.7.With the average degree 〈 k〉=4,the average number of hops under two routing strategies with different node sizes:(a) LAEE evolution model;(b) improved random geometric graph model.Each point is the average of 10 runs.

圖8 平均度 〈 k〉=4 時,不同節點規模下兩種路由方式的網絡最大吞吐量 Rc 的比較 (a) LAEE 演化模型;(b)改進的隨機幾何圖模型.圖中每個點是10 次仿真的平均值Fig.8.With the average degree 〈 k〉=4 ,Rc under two routing strategies with different node sizes:(a) LAEE evolution model;(b) improved random geometric graph model.Each point is the average of 10 runs.

不同路由策略下平均路徑長度、平均跳數與平均度〈k〉的關系如圖9 和圖10 所示.與改變網絡規模類似,這里也可以看到,無論平均度如何變化,最少跳數路由總是具有更小的平均跳數,而最短路徑長度路由總是具有更小的平均路徑長度.另一方面,隨著〈k〉的增加,網絡中的連邊數逐漸增加,各節點間路徑有了更多的選擇,因此傳輸的路徑長度變短,平均跳數減小.

圖9 節點數 N =1000 時,不同平均度下兩種路由方式平均路徑長度的比較 (a) LAEE 演化模型;(b)改進的隨機幾何圖模型.圖中每個點是10 次仿真的平均值Fig.9.With N=1000,the average path length under two routing strategies with different average degrees:(a) LAEE evolution model;(b) improved random geometric graph model.Each point is the average of 10 runs.

圖10 節點數 N =1000 時,不同平均度下兩種路由方式平均跳數的比較 (a) LAEE 演化模型;(b)改進的隨機幾何圖模型.圖中每個點是10 次仿真的平均值Fig.10.With N=1000,the average number of hops under two routing strategies with different average degrees:(a) LAEE evolution model;(b) improved random geometric graph model.Each point is the average of 10 runs.

圖11 給出了網絡最大吞吐量Rc隨平均度〈k〉的變化情況.總體來看,最短路徑長度路由總是具有更大的Rc值.而隨著平均度的不斷增大,網絡連接越來越稠密,負載傳輸的路徑越來越均勻地分布在網絡中,結果是導致Rc值的迅速增加,即網絡吞吐量迅速變大.

圖11 節點數 N =1000 時,不同平均度下兩種路由方式的網絡最大吞吐量 Rc 的比較 (a) LAEE 演化模型;(b)改進的隨機幾何圖模型.圖中每個點是10 次仿真的平均值Fig.11.With N =1000 ,R c under two routing strategies with different average degrees:(a) LAEE evolution model;(b) improved random geometric graph model.Each point is the average of 10 runs.

圖12 和圖13 分別給出了兩種網絡在采用兩種路由策略時的介數分布.可以看出,無論哪種網絡,采用最短路徑長度路由時的最大介數值都比采用最少跳數路由時的最大介數小.正是這個更小的最大介數,導致最短路徑長度路由具有更大的Rc.那么,為什么最短路徑長度路由會導致更小的最大介數呢? 這是因為采用最短路徑長度路由時,為了保證路徑長度盡可能短,所遵循的路徑更接近于直線,所以所謂網絡關鍵節點的作用并不突出.相比之下,最少跳數路由追求更少的跳數,網絡中少量關鍵節點往往起到中介的作用,匯聚了大量的路徑,導致最大介數更大.綜上所述,最短路徑長度路由能使網絡傳輸的負載得到更加合理的分布,從而使網絡具有更大的吞吐量,是一種更加有效的路由策略.

圖12 LAEE 演化模型中,節點數N=1000,〈 k〉=4 時的介數分布 (a)最少跳數路由;(b)最短路徑長度路由Fig.12.Betweenness distribution of the LAEE network with N=1000,〈 k〉 =4:(a) Least number of hops routing strategy;(b) shortest path length routing strategy.

圖13 改進的隨機幾何圖模型中,節點數N=1000,〈 k〉 =4 時的介數分布 (a)最少跳數路由;(b)最短路徑長度路由Fig.13.Betweenness distribution of the improved random geometric graph with N=1000,〈 k〉 =4:(a) Least number of hops routing strategy;(b) shortest path length routing strategy.

5 結論

在空間網絡中,“最短路徑”可以有不同的解讀,傳統的最短路徑等效于跳數最少的路徑.而空間網絡中由于連邊具有長度屬性,最短路徑也可以理解為從源節點到目的節點所經過的所有連邊的長度之和(即路徑長度)最短.本文提出的最短路徑長度路由策略就是基于后者.通過在勻質和異質空間網絡上的仿真發現,這種新路由策略能夠有效提升網絡最大吞吐量.本文提出的路由策略對現實生活中交通運輸、無線通信網絡等都具有很好的借鑒意義.