開(kāi)放對(duì)流環(huán)境下合作反應(yīng)擴(kuò)散對(duì)流模型的解的全局定性分析①
劉青蘭,張國(guó)洪
西南大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 重慶 400715
種群之間互惠共生是自然界中一種常見(jiàn)的生態(tài)學(xué)關(guān)系. 許多數(shù)學(xué)家和生態(tài)學(xué)家提出了不同的數(shù)學(xué)模型來(lái)刻畫(huà)物種之間相互合作的關(guān)系[1-2]. 特別地, 文獻(xiàn)[3]提出了下列合作互惠模型:
(1)
其中:u和v代表兩個(gè)合作種群的密度,ai(i=1,2)代表種群內(nèi)在增長(zhǎng)率,a1c1和a2c2代表種群內(nèi)競(jìng)爭(zhēng)系數(shù), 物種u和v的環(huán)境容納量分別為K1+b1v和K2+b2u, 可以看出其中一個(gè)種群的存在有利于另一個(gè)種群的生長(zhǎng), 系數(shù)ai,bi,ci和Ki(i=1,2)都是正常數(shù). Albrecht證明了系統(tǒng)(1)存在唯一全局漸近穩(wěn)定的正穩(wěn)態(tài)解. 在模型(1)的基礎(chǔ)上, 文獻(xiàn)[4-6]考慮了擴(kuò)散和交叉擴(kuò)散條件下系統(tǒng)非常數(shù)正平衡解的存在性問(wèn)題; 文獻(xiàn)[7-8]則進(jìn)一步研究了兩個(gè)互惠種群在自由邊界條件下是否能夠入侵的條件.
近年來(lái), 對(duì)流環(huán)境中的種群動(dòng)力學(xué)行為得到了大量的研究, 如河流中的相互競(jìng)爭(zhēng)種群、 捕食-食餌種群, 相應(yīng)的動(dòng)力學(xué)模型一般為反應(yīng)擴(kuò)散對(duì)流模型. 研究發(fā)現(xiàn)對(duì)流的引入對(duì)相互競(jìng)爭(zhēng)種群及捕食食餌系統(tǒng)的動(dòng)力學(xué)行為有重要的影響[9-11]. 基于上述分析, 一個(gè)自然的問(wèn)題就是對(duì)流的引入對(duì)以上互惠共生種群模型(1)的動(dòng)力學(xué)行為有什么影響, 即研究下列反應(yīng)-擴(kuò)散-對(duì)流合作模型:
(2)
其中:u(x,t)和v(x,t)是兩個(gè)互惠物種的種群密度;ai,bi,ci,Ki(i=1,2)的意義與系統(tǒng)(1)相同; 正常數(shù)d1,d2代表擴(kuò)散系數(shù),q1,q2代表兩個(gè)種群非負(fù)的對(duì)流速率;L是棲息地的大小. 在上游x=0處, 我們假設(shè)物種滿足無(wú)通量邊界條件, 這意味著不允許任何個(gè)體通過(guò)該邊界. 在下游x=L處, 我們假設(shè)為自由流邊界條件, 在文獻(xiàn)[12]中, 該邊界條件被稱(chēng)為Danckwerks邊界條件, 它用來(lái)刻畫(huà)小溪流向湖泊的自然情況.
1 系統(tǒng)的耗散性
本節(jié)將證明系統(tǒng)(2)存在唯一一個(gè)正解, 它對(duì)所有的x∈[0,L]和t>0都有界.
定理1對(duì)任意非負(fù)非平凡初值函數(shù)(u0(x),v0(x)), 系統(tǒng)(2)都有唯一一個(gè)非負(fù)解(u(x,t),v(x,t)), 且存在兩個(gè)僅依賴(lài)初值(u0(x),v0(x))的正常數(shù)M1,M2使得
0
證首先, 由強(qiáng)極大值原理可得u(x,t)>0以及v(x,t)>0. 然后取正常數(shù)M1和M2使得
則容易驗(yàn)證(M1,M2)和(0, 0)是系統(tǒng)(2)的一對(duì)有序的上下解. 由文獻(xiàn)[14]的定理8.3.1得系統(tǒng)(2)在S(0, 0;M1,M2)上有唯一解, 其中
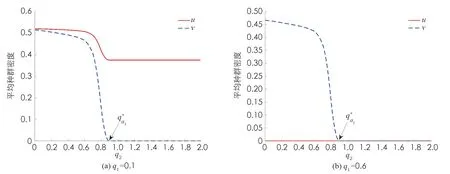
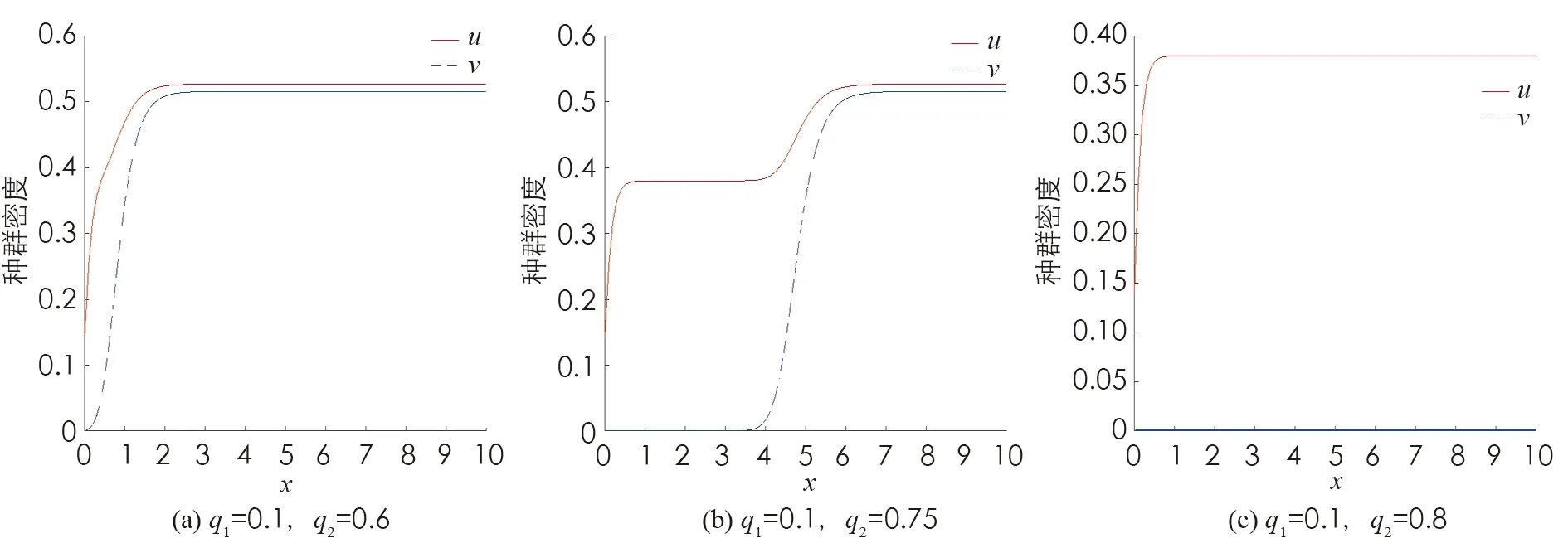
S(0, 0;M1,M2)={(u,v)∈C([0,L]×[0, +∞)); 0 定理證畢. 本節(jié)研究系統(tǒng)(2)的平衡態(tài)解的存在性和穩(wěn)定性. 我們首先回顧以下單種群模型的相關(guān)結(jié)論: (3) 以及 (4) 與(3)式相應(yīng)的特征值問(wèn)題如下: (5) (6) (7) 其中:λ1(q2,a2)是(5)式中d1,q1,a1被d2,q2,a2替代后的系統(tǒng)的主特征值. 由文獻(xiàn)[9]的定理2.1(b)可得單種群模型(3)和(4)的如下結(jié)果. 證我們首先證明半平凡穩(wěn)態(tài)解(0,θq2)是局部漸近穩(wěn)定的. 為此, 把(2)式對(duì)應(yīng)的穩(wěn)態(tài)系統(tǒng)在(0,θq2)處線性化, 可以得到如下相應(yīng)的特征值問(wèn)題: (8) 接下來(lái)證明在非負(fù)和非平凡初始條件下, 系統(tǒng)(2)的解(u(x,t),v(x,t))收斂到(0,θq2). 由拋物方程的極大值原理可得系統(tǒng)(2)的解(u(x,t),v(x,t))對(duì)所有x∈[0,L]和t>0, 都滿足u(x,t)>0,v(x,t)>0. 因此, 在(0,L)×(0, +∞)上, ut≤d1uxx-q1ux+a1u 從而由拋物方程的比較原理可推出對(duì)任意x∈[0,L]和t>0, 有u(x,t)≤U(x,t), 其中U(x,t)滿足 即對(duì)任意的ε>0, 存在T1>0, 使得對(duì)所有的x∈[0,L]和t>T1, 都有u(x,t)<ε. 故在(0,L)×(T1, +∞)上 (9) (10) 同時(shí), 由(9)式右邊不等式以及拋物方程比較原理可得對(duì)x∈[0,L]和t>T1, 有v(x,t)≤Vε(x,t), 其中Vε(x,t)滿足 (11) 證為了證明半平凡穩(wěn)態(tài)解(θq1, 0)是局部漸近穩(wěn)定的, 把(2)式對(duì)應(yīng)的穩(wěn)態(tài)系統(tǒng)在(θq1, 0) 處線性化, 可以得到如下相應(yīng)的特征值問(wèn)題: (12) 證首先證明系統(tǒng)(2)的平凡穩(wěn)態(tài)解(0, 0)是局部漸近穩(wěn)定的. 事實(shí)上, 只需考慮以下特征值問(wèn)題: (13) 本節(jié)致力于研究初始條件為u(x, 0)=u0(x)(u0(x)≥0且u0(x)?0)和v(x, 0)=v0(x)(v0(x)≥0且v0(x)?0)時(shí)系統(tǒng)(2)的解(u(x,t),v(x,t))的一致持續(xù)性. 證我們使用抽象持久性理論[15]來(lái)證明這個(gè)定理. 首先定義Θ(t)是狀態(tài)空間P上系統(tǒng)(2)的解半流, 其中在[0,L]上, P={(u,v)∈C[0,L]×C[0,L]:u≥0,v≥0} 令P0={(u,v)∈P:u(x)?0,v(x)?0}, ?P0=PP0. 由極大值原理可得若(u0,v0)∈P0, 則對(duì)任意的x∈[0,L]和t>0, 系統(tǒng)(2)的解都滿足u(x,t)>0,v(x,t)>0. 因此,P0在P中是開(kāi)的, 且在系統(tǒng)(2)生成的動(dòng)力學(xué)下是前向不變的, 即對(duì)所有t≥0, 有Θ(t)P0?P0. 再者, ?P0包含平衡點(diǎn)(0, 0), (θq1, 0)和(0,θq2). 剩下的證明分為以下5個(gè)步驟. 1) 令M?={(u0,v0)∈?P0:Θ(t)(u0,v0)∈?P0, ?t≥0},ω((u0,v0))是正向軌道γ+((u0,v0))={Θ(t)(u0,v0) :t≥0}的ω極限集. 先證明 2) 證明(0, 0)是一致的弱排斥子, 即存在δ1>0, 使得對(duì)任意的(u0,v0)∈P0, 都有 (14) 由比較原理得出對(duì)任意的t≥t0,x∈[0,L], 有 3) 證明(θq1, 0)是一致的弱排斥子, 即存在δ2>0, 使得對(duì)任意的(u0,v0)∈P0, 都有 (15) ‖u(x,t, (u0,v0))-θq1‖<δ, ‖v(x,t, (u0,v0))‖<δ 從比較原理得出對(duì)任意t≥t1,x∈[0,L], 有 4) 證明(0,θq2)是一致的弱排斥子, 它是P中的孤立不變集. 這個(gè)證明類(lèi)似于第3步, 此處省略. 其中Ws({(0, 0)}),Ws({(θq1, 0)})和Ws({(0,θq2)})分別是(0, 0),(θq1, 0)和(0,θq2)的穩(wěn)定集[15]. 因此{(lán)(0, 0)}∪{(θq1, 0)}∪{(0,θq2)}的子集在?P0中沒(méi)有形成一個(gè)圈. 從而由文獻(xiàn)[15]的定理3可得: 存在η>0, 使得對(duì)任意的(u0,v0)∈P0, 有 本節(jié)通過(guò)數(shù)值模擬研究對(duì)流速率對(duì)系統(tǒng)(2)動(dòng)力學(xué)行為及種群空間分布的影響. 由前面的理論分析已經(jīng)知道兩個(gè)共生種群的對(duì)流速率q1,q2對(duì)系統(tǒng)(2)的動(dòng)力學(xué)行為有很大的影響. 取d1=0.01,d2=0.02,a1=2,a2=3,K1=0.4,K2=0.5,b1=0.3,b2=0.1,c1=0.1,c2=0.2和L=10, 并通過(guò)改變q1,q2的值來(lái)觀察系統(tǒng)(2)的各種動(dòng)力學(xué)性態(tài)的變化. 圖1 對(duì)流速率q2對(duì)系統(tǒng)(2)動(dòng)力學(xué)性態(tài)的影響 接下來(lái), 我們關(guān)注對(duì)流速率對(duì)種群在河流[0,L]中密度分布的影響. 先固定對(duì)流速率q1, 然后取不同的q2來(lái)觀察這兩個(gè)共生物種在河流[0,L]中的分布情況. 通過(guò)數(shù)值模擬發(fā)現(xiàn), 當(dāng)對(duì)流速率q2很小時(shí), 兩個(gè)物種共存, 且在整條河流都有分布(圖2(a)). 當(dāng)對(duì)流速率q2逐漸增大時(shí), 兩個(gè)物種仍然可以共存, 但種群v已經(jīng)被沖到河流下游, 生存區(qū)域變小, 導(dǎo)致平均密度降低, 同時(shí)使得互惠種群u的平均密度也降低(圖2(b)). 當(dāng)對(duì)流速率q2足夠大時(shí), 物種v將滅絕(圖2(c)). 對(duì)流速率q1的變化對(duì)兩個(gè)種群的密度分布影響是相似的, 在此不再贅述. 圖2 對(duì)流速率q2對(duì)系統(tǒng)(2)的種群密度分布的影響2 種群的滅絕性

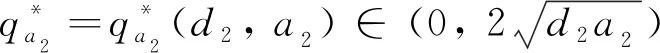










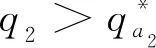


3 一致持續(xù)性
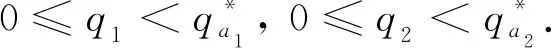



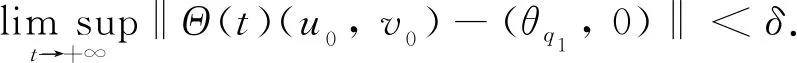






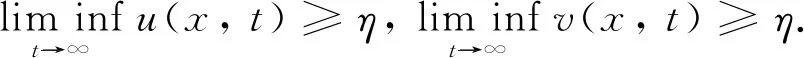
4 數(shù)值模擬

5 結(jié)論及討論


