解非線性半定規劃的一種回溯線搜索型算法①

李丹丹，王松華，李遠飛

1.廣州華商學院 應用數學系， 廣州 511300；2.百色學院 數學與統計學院， 廣西 百色 533000

考慮如下非線性半定規劃問題(NLSDP)：

(1)

線性半定規劃[1-2]是優化領域中最經典的問題， 然而眾多實際問題屬于非線性半定規劃問題， 如工程設計、 最優控制、 經濟、 金融等領域[3-4]． 因此， 非線性半定規劃的研究具有理論創新和實際應用的意義． 若干有效方法可求解非線性半定規劃問題且其效果顯著， 如增廣拉格朗日方法[5]、 序列半定規劃方法[6]、 序列線性方程組方法[7]、 乘子法[8]、 原始-對偶內點法[9]， 其中序列半定規劃方法應用較廣． 很多學者將優良的非線性規劃算法推廣到非線性半定規劃問題中， 如文獻[10]借鑒傳統非線性規劃的子問題修正技術， 并結合信賴域框架， 提出了求解非線性半定規劃的一個無可行性恢復階段的濾子算法． 文獻[11]采用非單調線搜索技術來保證目標函數或約束違反度函數的充分下降， 從而提出一個求解非線性半定規劃的無罰無濾序列二次半定規劃算法． 文獻[12]提出一個求解帶有不等式約束的非線性規劃全局收斂性算法， 該算法的接受準則既不使用罰函數也不使用濾子， 且效果顯著． 本文在文獻[12]的基礎上， 將該思想推廣到非線性半定規劃中， 提出一個求解非線性半定規劃問題的無罰函數無濾子回溯線搜索型序列半定規劃算法．

1 算法描述

二階連續可微函數f(x)的梯度和Hesse矩陣分別記為f(x)和2f(x)． 二階連續可微向量函數h(x)： =(h1(x)，h2(x)， …，hp(x))T， 則稱矩陣Dh(x)=(h1(x)，h2(x)， …，hp(x))T∈Rp×n為h(x) 的雅可比矩陣． 二階連續可微矩陣函數G(x)， 記其微分算子DG(x)為

且對任意的d∈Rn

記其伴隨算子DG(x)*為

其中Z∈Sm．

記NLSDP(1)的拉格朗日函數為

L(x，λ，Y)=f(x)+λTh(x)+〈Y，G(x)〉

其中x∈Rn，λ∈Rp，Y∈Sm．

定義1若x*∈Rn是NLSDP(1)的可行點， 且存在向量λ*∈Rp和矩陣Y*∈Sm滿足如下條件：

xL(x*，λ*，Y*)=f(x*)+Dh(x*)Tλ*+DG(x*)*Y*=0

h(x*)=0，G(x*)?0，Y*0， 〈G(x*)，Y*〉=0

則稱(x*，λ*，Y*)是NLSDP(1)的一個KKT點對， (λ*，Y*)是在x*處相對應的拉格朗日乘子．

本文采用線搜索型序列半定規劃方法框架， 設當前迭代點為xk∈Rn， 定義產生搜索方向的二次半定子問題QSD(xk，Bk) 如下：

(2)

其中矩陣Bk∈Rn×n是NLSDP(1)的拉格朗日函數的Hesse陣或其近似陣． 若QSD(xk，Bk)存在最優解， 則記其解為dk． 同時， 為了度量NLSDP(1)的約束可行性， 下面給出其約束違反度函數的定義：

θ(x)=λ1(G(x))++‖h(x)‖

其中λ1(A)表示矩陣A的最大特征值， (α)+=max{0，α}， (λ1(G(x)))+簡記為λ1(G(x))+． 顯然， 若θ(x)=0， 則x為NLSDP(1) 的可行解．

(3)

pred(xk)=-f(xk)Tdk

(4)

因此， 定義目標函數f(x)的非單調充分下降性條件：

nared(xk)≥ηαk，lpred(xk)

(5)

其中η∈(0， 1)， 這不同于單調充分下降性條件：

(6)

(7)

其中β∈(0， 1)．

最后， 下面給出算法的接受準則． 如果約束違反度函數θ(x)滿足非單調充分下降性條件， 即(7)式成立， 或目標函數f(x)具有適當的下降量且約束違反度函數值有個合理的上界， 即

(8)

成立， 其中γ∈(0， 1)． 那么考慮以下兩種情況．

1) 若

pred(xk)≤ξ(dk)TBkdk

(9)

且

(10)

2) 若

pred(xk)>ξ(dk)TBkdk

(11)

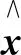
(12)

其中γα∈(0， 1)，sθ≥1．

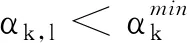
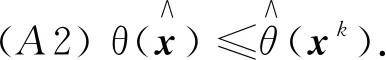
可行性恢復階段的具體細節見文獻[10]．

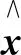
基于以上討論， 下面給出求解NLSDP(1)的算法描述：

算法1

步驟1令flag=0， 求解子問題QSD(xk，Bk)． 若QSD(xk，Bk)存在最優解， 則記為dk， 否則算法進入可行性恢復階段， 轉步驟7． 若dk=0， 則算法停止．

步驟3(回溯線搜索)

步驟3.1令l=0，αk，0=1．

步驟3.3若(7)式和(8)式不成立， 則轉步驟3.5．

步驟3.4若(9)式和(10)式成立， 則令flag=1， 轉步驟4． 若(5)式和(11)式成立， 則轉步驟4．

步驟3.5令αk， l+1=ραk， l，l=l+1， 轉步驟3.2．

步驟4令αk=αk， l，xk+1=xk+αkdk．

步驟6(更新步)利用某種方法， 更新Bk為對稱正定矩陣Bk+1． 令k=k+1， 轉步驟1．

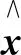
2 全局收斂性

本節將分析算法1的全局收斂性， 為此， 需作如下合理假設：

(B1) 迭代點列{xk}和{xk+αk，ldk}在緊凸集χ中．

(B2)f(x)，h(x)，G(x)在緊凸集χ中二階連續可微．

(B3) 矩陣Bk為對稱正定矩陣， 且存在常數a，b>0， 對任意的d∈Rn有a‖d‖2≤dTBkd≤b‖d‖2．

注1不失一般性， 由假設B可知， 對于任意x∈χ， ‖2f(x)‖≤b， ‖D2h(x)‖≤b， ‖D2G(x)‖≤b．

引理1對于任意的k， 以下不等式成立：

于是有

因此， 當k充分大時

2) 假定θ型迭代發生無限次， 那么存在指標k2， 使得當k>k2時，θ型迭代發生， 由(10)式和引理2， 可知結論成立．

引理4在假設B條件下， 子問題QSD(xk，Bk)的可行解d滿足以下不等式：

(13)

(14)

證由(3)式、 (4)式、 Taylor展開式和假設B可得

其中ξ1介于xk和xk+αk，ld之間． 類似地， 由Taylor展開式可推出

引理5在假設B成立下， NLSDP(1)的可行點x*滿足MFCQ條件， 但不是KKT點． 那么存在x*的鄰域N(x*)及正常數η1， 使得當xk∈N(x*)∩χ時， 子問題QSD(xk，Bk)的可行集非空， 且其最優解dk滿足

(15)

證類似文獻[14]的引理4.7可證結論成立．

引理6在假設B條件下，dk是子問題QSD(xk，Bk)的最優解， 那么若

(16)

且

(17)

證若

則由引理4和引理5得

故nared(xk)≥ηαk，lpred(xk)成立． 結合引理4和引理5， 由(16)和(17)式有

故nared(xk)≥γθ(xk+αk，ldk)成立．

引理7在假設B條件下， 線搜索(步驟3)是有限步終止的．

綜上所述， 若

(18)

則xk+αk，ldk被算法所接受，f型迭代發生， 矛盾．

定理1若假設B成立， 則下面結論之一成立：

(C2) 算法有限步終止， 即存在某個迭代點xk為NLSDP(1)的KKT點．

(C3) 算法產生的迭代點列{xk}收斂于聚點x*且該聚點x*為NLSDP(1)的可行解， 那么x*或是NLSDP(1)的KKT點， 或是x*不滿足MFCQ條件．

證不失一般性， 假設結論(C1)和(C2)都不成立， 下面討論兩種情況分別證明結論(C3)成立．

即x*是NLSDP(1)的可行點．

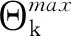
3 數值試驗

為了驗證算法1的可行性， 本節給出了算法的初步數值實驗， 采用MATLAB(2014a)軟件實現算法， 程序在配置Windows 10， 8G RAM， 3.60 GHz CPU的計算機上運行． 子問題QSD(xk，Bk)使用文獻[15] SDPT3求解． 算法采用BFGS公式對Bk更新為Bk+1， 其更新公式見文獻[16]． 下面給出算例問題如下：

1) Rosen-Suzuki問題： 測試算例來源于文獻[17]：

其數值結果見表1．

2) SOFP問題． 測試算例來源于文獻[18]：

其中：QF=CTFTFC+I；AF=A+BFC； 矩陣變量L為實對稱的； 矩陣變量F不是方陣；A，B，C為常量矩陣． 該問題的數值結果見表2．

表2 SOFP問題數值結果

3) NCMP問題． 測試算例來自于文獻[9]：

其中：A=(aij)(∈Sm)是給定的， 且其對角線元素aii=1(i=1，2，…，m)， 其余元素隨機取自[-1， 1]； 選取ε=10-3． 數值結果見表3．

表3 NCMP問題數值結果

在數值試驗中， 選取的參數如下：

η=0.001，τ=0.01，ξ=0.01，γ=0.001，γα=0.99，sθ=2，β=0.999，ρ=0.5

終止準則為‖dk‖≤10-4， 設置算法1的迭代次數上限為200． 下面給出表1-3中的符號含義如下：x0為初始點；Ndf為目標函數梯度計算次數； problem為COMPleib算例庫算例名稱；Iter為算法迭代次數；n為自變量維數；ri為可行性恢復階段使用次數；p為等式約束的維數；θ*為最優點約束違反度函數值；m為半定約束矩陣維數；f*為最優目標函數值；Nf為目標函數計算次數；t為計算機運行時間(含可行性恢復階段用時)．

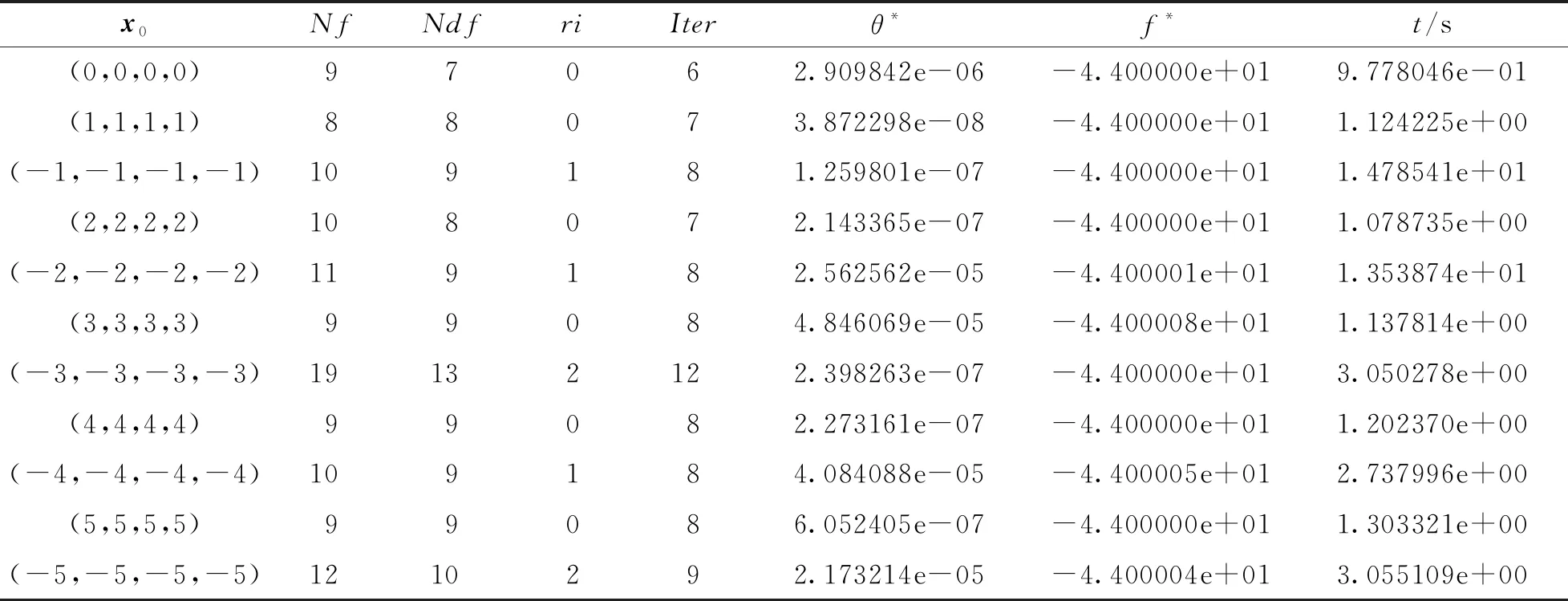
表1 Rosen-Suzuki問題數值結果

續表2

4 小結

本文提出一種新的求解非線性半定規劃的無罰無濾回溯線搜索型序列半定規劃算法， 新方法基于傳統的二次規劃子問題構建二次半定子問題， 通過求解該子問題產生搜索方向， 為了避免使用罰函數和濾子， 采用回溯線搜索技術來保證目標函數值或約束違反度函數值充分下降． 而非單調的充分性下降條件使得試探點更加容易被算法接受． 同時在合理的假設條件下， 證明了該算法的適定性以及全局收斂性， 最后初步的數值試驗結果表明了該算法的有效性．