基于模糊和聲搜索算法的光伏MPPT控制研究

梁智超，李夢達，鄭旭彬，姚林萍

(上海電機學院電氣學院，上海 201306)

太陽能是世界上最豐富的清潔能源之一，研究太陽能光伏發電對促進“碳達峰，碳中和”[1]具有積極意義。近年來，通過最大功率點跟蹤(maximum power point tracking，MPPT)的控制來提高光伏電池陣列的太陽能轉換效率備受關注，其主要挑戰在于如何在非均勻光照下的多峰值P-V 曲線實現快速精確的跟蹤。目前已有很多學者研究不同的MPPT 算法，文獻[2]提到的擾動觀察法和電導增量法在在步長選擇上容易出現問題，對于局部陰影或者外界環境劇烈變化下的多峰值的P-V 曲線容易陷入局部功率極值點的情況；文獻[3]提到的粒子群算法能夠解決局部陰影情況下的跟蹤精度不足問題，但是個體位置變化隨機性大，搜索過程中功率震蕩較大，在1 s附近才趨于穩定，收斂慢，且參數設置較為復雜，在變化的環境下可能會導致MPPT 失效；文獻[4]提到的和聲搜索算法對多峰值曲線全局尋優能力強，但收斂速度依賴于算法參數的設置。

本文提出一種基于模糊和聲搜索(fuzzy harmony search，FHS)算法的光伏MPPT 控制方法，通過模糊控制的思想優化和聲搜索算法MPPT，根據多峰值光伏電池功率特性曲線變化規律作為專家經驗，設置相應的模糊規則，在MPPT 中自適應地平衡全局搜索與局部搜索，提高搜索速度和精度。該算法全局功率搜索能力強，對MPP 的跟蹤精度高，收斂速度快且更加穩定。

1 光伏電池陣列

1.1 光伏電池數學模型

光伏電池陣列的輸出特性易受光照強度、環境溫度及工作負載影響[4]。單個PV 的等效電路圖如圖1 所示。

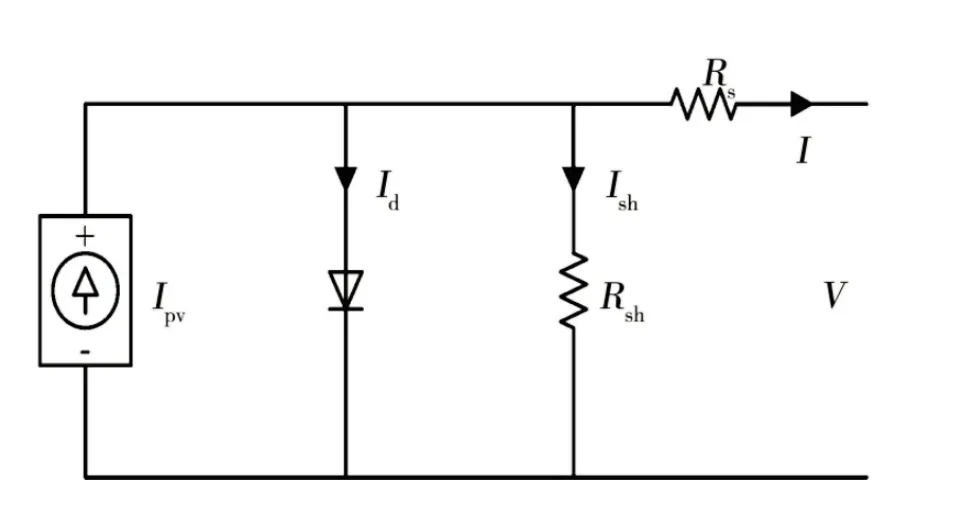
圖1 光伏電池等效電路圖

其輸出特性方程如式(1)：

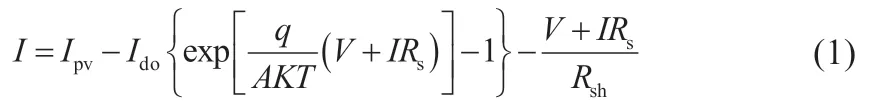
式中：Ipv、Ido、Ish分別為光生電流、輸出電流、二極管反向飽和電流；Rs、Rsh分別為等效串聯和并聯電阻；K、q、A分別為玻爾茲曼常數、電子電荷常數、光伏電池特性常數；T為工作溫度。

1.2 光伏電池陣列輸出特性分析

為突出本文所研究的局部陰影情況(PSC)對光伏陣列輸出的影響，在四塊光伏電池上給定非均勻的光照強度仿真，在給定的標準溫度25 ℃下進行仿真。為了驗證本文的MPPT 算法是否能在光照突變后依舊能快速跟蹤到全局最大功率點，故設置兩組不同的光照強度分別為：工況一PSC1：1 000、1 000、800 和500 W/m2；工況二PSC2：500、500、400 和250 W/m2。對應的P-V 曲線如圖2 所示。

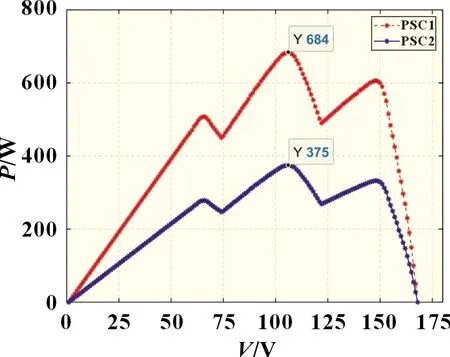
圖2 光伏電池P-V特性曲線

由圖2 可知，光伏電池陣列在非均勻光照工況下，P-V 特性曲線出現明顯的多峰值現象，常規的MPPT 算法在多峰值尋優過程中容易誤跟蹤到局部極值功率點，導致MPPT 難以發揮最佳的效果，降低了光伏電池陣列整體的能量輸出，因此需要研究全局性多峰值快速尋優的MPPT 算法。

2 基于FHS 算法的MPPT 算法

2.1 標準和聲搜索算法(HS)

和聲搜索算法[5]是一種啟發式全局搜索算法，在和聲彈奏中，樂師們憑借記憶，通過重復調試和聲音調，彈奏出最優美的和聲，該算法由和聲記憶庫和相關和聲調整參數組成[6]，算法基本流程如下：

(1)由和聲記憶庫(HM)產生初始解HMS個，優美和聲評估函數為f(x)，見式(2)：

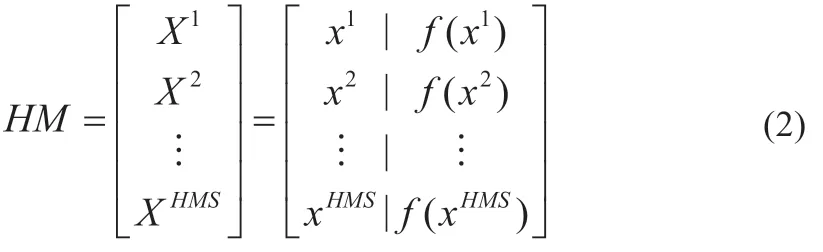
(2)算法每輪迭代在和聲音調保留概率(PHMCR)外產生隨機新的和聲音調xnew，見式(3)：

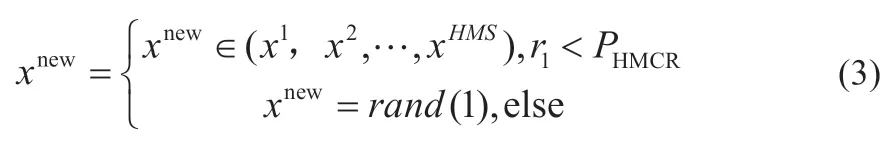
(3)以音調調節概率(PPAR)按一定的音調調節步長(BW)進行擾動去調整現有和聲音調，見式(4)：

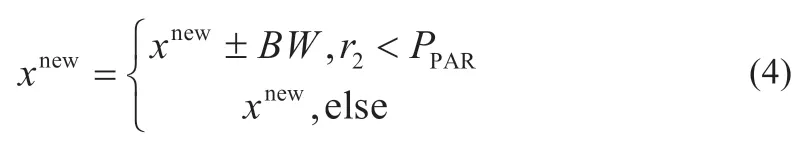
式中：r1、r2∈[0,1]。

(4)通過和聲(功率大小)評估，對比和聲記憶中最差功率值，若新的功率值優于最差功率值則進行替換，更新到和聲記憶庫中進行功率輸出。

2.2 引入模糊自適應因子

在本文的MPPT 算法中，光伏輸出功率對應為和聲尋優變量，占空比對應為音調步長調節變量，將模糊控制思想與和聲搜索算法結合運用于步驟S3 中，根據多峰值光伏電池陣列的P-V 功率曲線的特性來設置模糊規則，引入模糊自適應因子k，在MPPT 中對功率和聲f(x)=Vpv·Ipv進行評估對比，通過模糊自適應因子k對音調調節步長BW進行動態調整，算法前期較大的BW有利于獲得更好的全局搜索能力，快速搜索到最優和聲附近，隨著迭代次數的增加，根據設置的模糊規則自適應調整BW，最終獲得最優和聲。

本文所提出的模糊控制器總共有兩個輸入量NI和E及一個輸出量k。第一個輸入量為迭代次數NI，由于非均勻光照下所進行尋優的光伏陣列P-V 曲線通常是前期平緩穩定，中后期是呈多峰狀，考慮其曲線特性，NI的模糊論域設為[0,150]，子集為{L,LM,M,MH,H}，表示迭代次數NI的遞增；前期音調調節步長BW較大有利于大范圍搜索，能提高算法的搜索速度和全局能力；隨著迭代次數NI增加，此時BW值應自適應減小，進行小范圍精細搜索。

第二個輸入量為光伏輸出功率誤差E，由式(5)定義：

式中：Ei為第i次迭代的功率誤差；Pi為第i次迭代搜索到的最大功率值；Pi－1為第i－1 次迭代的較差功率值。二者的誤差輸入到模糊控制器中。為了實現在不同功率誤差下的快速跟蹤，E的模糊論域設為[0,0.5]，子集為{L,LM,M,MH,H}，表示功率誤差的遞增；當E較大，表示此時功率點離最大功率點較遠，輸出較大的k值調整BW，在大范圍內進行和聲搜索，保證其全局功率點搜索能力；當E較小，表示此時功率點已接近最大功率點，應使k值減小，降低BW值，縮小搜索范圍，讓其實現精準的局部搜索，保證其搜索精度。

k定義為模糊自適應因子，為模糊控制器的輸出量，用于和聲音調調節步長BW的自適應調整，達到平衡搜索速度與跟蹤精度，提高算法的全局搜索能力的目的，關系如下：

模糊控制器輸出k的模糊論域為[0,1]，子集為{VL,L,ML,LM,M,HM,MH,H,VH}，表示BW對應調節為很低、低、中低、低中、中、高中、中高、高、很高。

算法初期，當離最大功率點遠時，需要較大的BW值進行全局搜索，應使k值較大，隸屬度函數選擇較緩三角形，取值稍大，搜索范圍廣；隨著迭代的進行，算法逐漸靠近全局最大功率點，此時需要快速減少BW值，減小搜索震蕩，應使k值較小，隸屬度函數選用較陡三角形，取值精細，搜索精度高。

綜上所述，NI、E、k的隸屬度函數設置如圖3 所示。

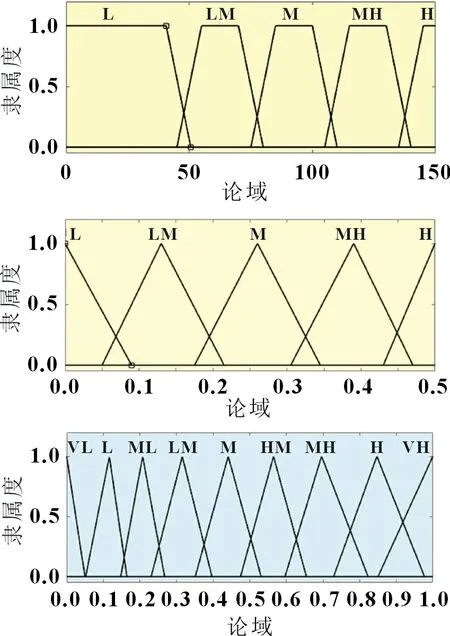
圖3 NI、E、k的隸屬度函數

根據上述經驗，模糊控制遵循的原則如表1 所示。

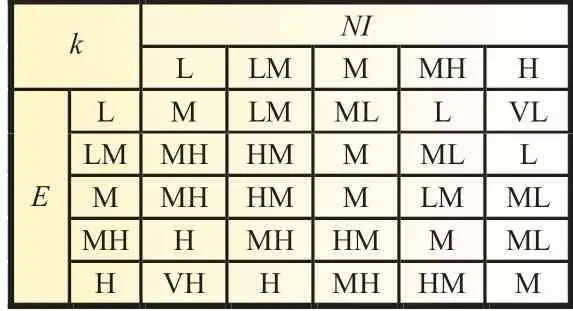
表1 模糊規則表

改進后結合模糊自適應優化參數的和聲音調更新公式為：

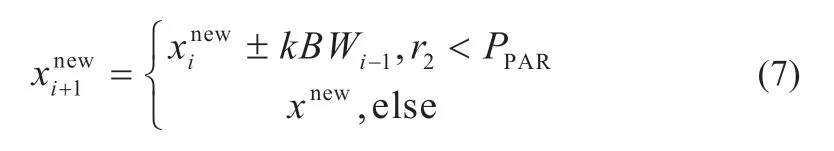
2.3 基于FHS 算法的MPPT 算法

根據上述內容，為解決非均勻光照下的多峰值MPPT 尋優問題，同時克服MPPT 尋優過程中的收斂速度與跟蹤精度無法兼顧的問題，提出了基于FHS 算法的MPPT 算法，并將其運用于光伏MPPT 中。

基于FHS 的MPPT 控制框圖如圖4 所示。首先，測量模型中光伏電池陣列的Vpv和Ipv作為輸入量，輸入到HS-MPPT算法模塊中，根據和聲功率評估函數f(x)=Vpv·Ipv的功率值對比進行迭代尋優，輸出當前占空比D，用于調節電壓值Vpv，獲得迭代后和聲功率值；同時，用HS 算法模塊中的迭代次數NI與功率誤差E作為輸入量，從模糊控制器中輸出自適應因子k來調節BW，對占空比D進行自適應調整，通過升壓電路獲得最優電壓，進行全局最大功率點跟蹤。

圖4 基于FHS的光伏MPPT結構模型

基于FHS 算法的MPPT 算法具體步驟如下：

S1.參數初始化，包括HMS、PHMCR、PPAR、BW和NI。

S2.初始化和聲記憶庫HM，得到HMS個初始和聲音調；式(2)中，初始和聲音調xi表示初始占空比D，為了保證算法的遍歷性，使占空比D在[0,1]區間內均勻分布，設置HMS=4個初始和聲音調，每個和聲音調的初始占空比為{x1,x2,x3,x4}=[0,0.3,0.6,0.9]。

S3.產生新解xnew。以PHMCR的概率在HM的占空比中進行初步功率評估，以(1－PHMCR)的概率獲得HM外的隨機占空比，然后通過式(6)的模糊因子以PPAR的概率對和聲記憶庫的占空比進行步長為BW的調節，獲得新的和聲音調占空比。

S4.更新和聲記憶庫HM。評估函數為f(xi)=P，新產生和聲功率進行評估，計算當前占空比下功率大小；若當前功率值優于最差值則進行替換，代表搜索到了更優的功率點，并將其更新至HM；否則，直接進入下一次和聲創作。

S5.檢查算法迭代次數有無達到NI，判斷是否重復步驟S3 和步驟S4。

圖5 為基于FHS 算法的MPPT 算法流程框圖。

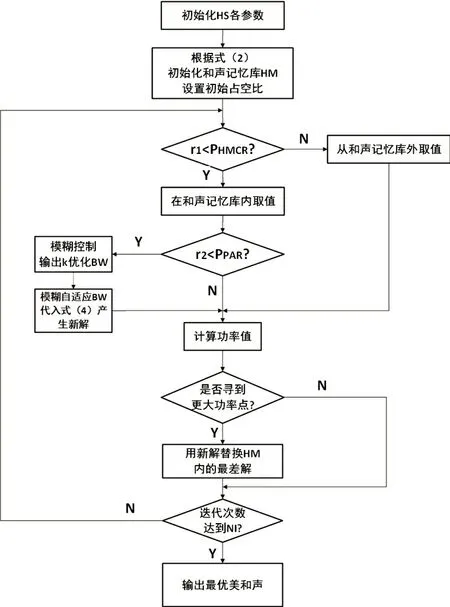
圖5 算法流程框圖

3 仿真分析

3.1 仿真模型

為驗證基于FHS 的MPPT 控制策略的高效性和穩定性，在MATLAB/Simulink 建立了光伏MPPT 仿真模型。光伏電池模塊參數為Uoc=43.6 V，Isc=8.35 A，Um=35 V，Im=7.6 A。使用擾動觀察法(P&O)、粒子群算法(PSO)、和聲搜索算法(HS)與模糊和聲搜索算法(FHS)分別在局部陰影和光照突變工況下進行靜態與動態的仿真效果對比。圖6 為基于FHS-MPPT的仿真實驗模型。

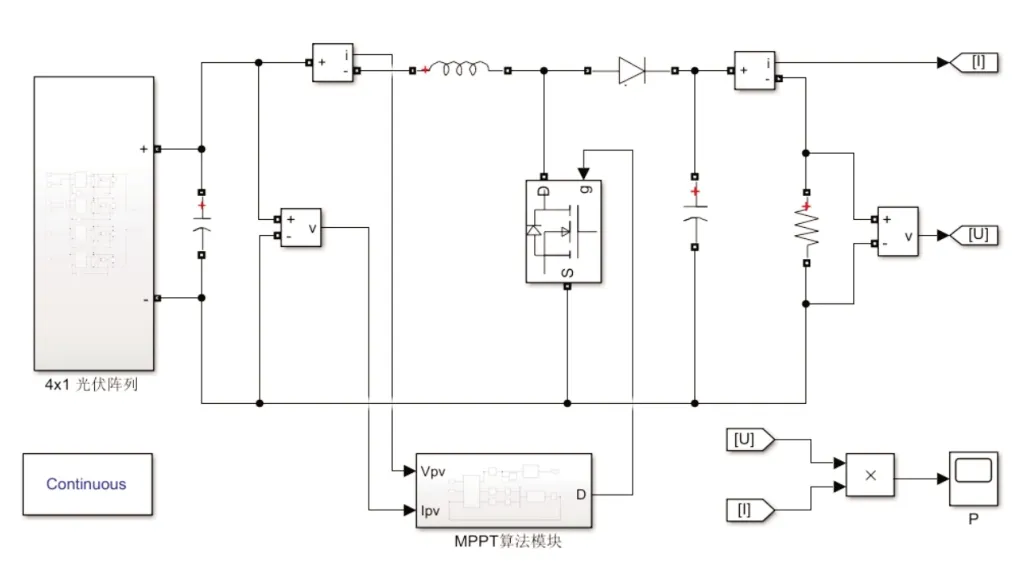
圖6 基于FHS-MPPT的仿真實驗模型

3.2 靜態仿真分析

靜態仿真模擬的是光伏電池陣列在局部陰影的非均勻光照下的最大功率點跟蹤，對多個最大功率點進行全局尋優。為驗證算法在多峰值P-V 曲線尋優的有效性，在標準溫度25 ℃工況PSC1 下進行仿真，由圖2 的工況PSC1 的P-V 特性可知，此時全局最大功率點為684 W，跟蹤精度為算法收斂后跟蹤的平均最大功率點與該工況下的全局最大功率點的比值。各MPPT 算法跟蹤效果如圖7 所示。

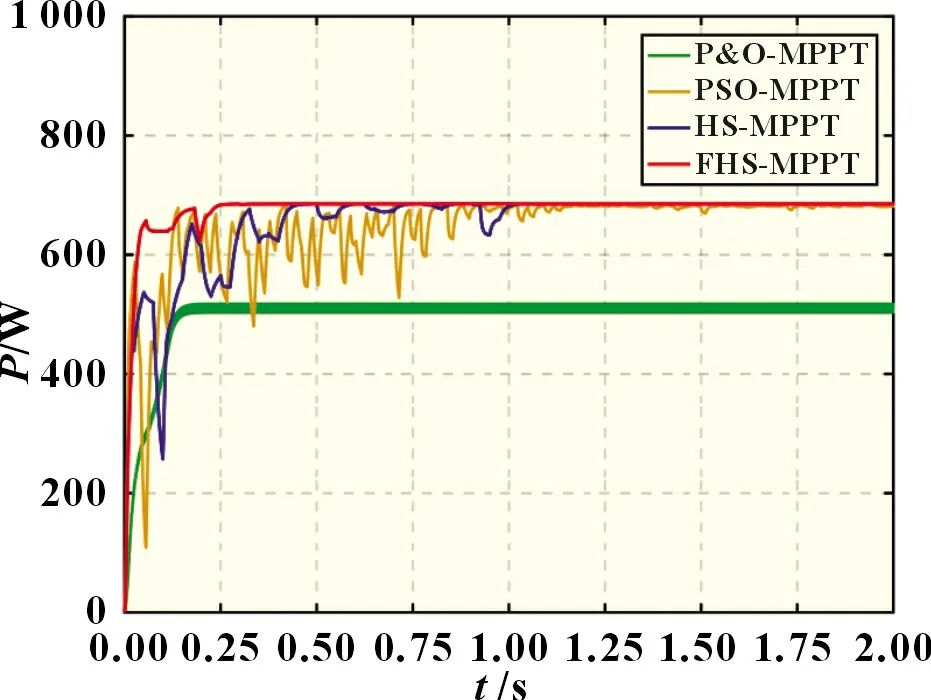
圖7 靜態仿真MPPT效果圖

由圖7 和表2 可知，P&O-MPPT 搜索到P-V 曲線的第一個波峰505 W 附近，明顯陷入局部最優，跟蹤精度約為73.88%，損失功率高達179 W，雖然收斂用時最短，為0.14 s，但跟蹤精度最低；PSO-MPPT 算法前期震蕩較大，收斂速度較慢，用時1.12 s，且收斂后仍存在8 W 左右的小幅搜索震蕩，跟蹤精度約為98.53%；本文提出的FHS-MPPT 算法能做到迅速收斂的同時兼顧高的跟蹤精度，用時僅0.25 s 就收斂到功率點681 W處，跟蹤精度高達99.56%，與全局最大功率點僅相差3 W。相較于傳統算法P&O-MPPT，本文所提算法獲得的功率值有176 W 的大幅提升，能夠兼顧收斂速度和跟蹤精度，在實現快速跟蹤的同時也能保持高的跟蹤精度；相較于智能算法PSO-MPPT和HS-MPPT，本文所提算法收斂速度更快，跟蹤到的最大功率值分別提高了7 和2 W，跟蹤精度有所提高，且搜索震蕩小，加強了光伏系統的穩定性，提高了太陽能的利用率。

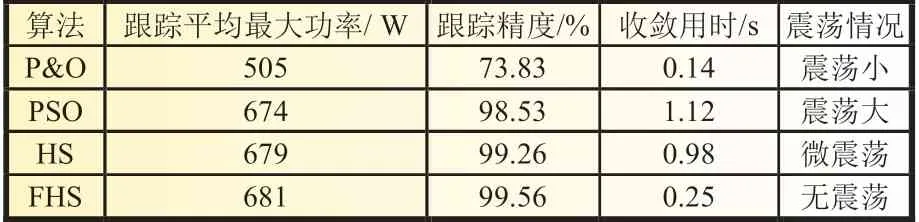
表2 靜態仿真性能對比表

3.3 動態仿真分析

實際上，由于受鳥類、落葉、移動云層等因素的動態影響，光伏電池陣列所處的環境是復雜多變的，故設置光照突變仿真組分析驗證算法應對光照突變的跟蹤能力，模擬的是在原有的局部陰影光照工況下，光照強度突然發生突變的狀況；當2 s時，光照強度從靜態工況PSC1突變到PSC2的500、500、400和250 W/m2，其P-V 特性曲線對比見圖2，突變后工況PSC2 的全局最大功率點為375 W，跟蹤效果仿真對比波形如圖8。

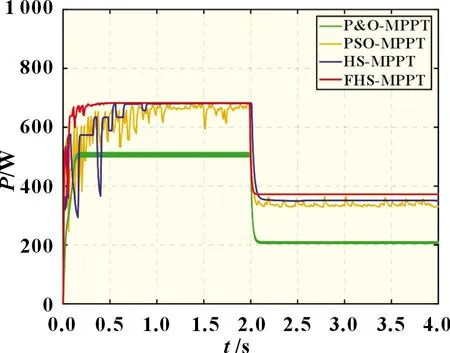
圖8 動態仿真MPPT效果圖

由圖8 和表3 可知，在光照突變情況下，P&O 算法跟蹤效果不佳；PSO 算法的震蕩幅度大，跟蹤精度僅有96.35%，光照突變后跟蹤精度降低為90.40%，且無法穩定收斂；本文所使用FHS 算法能一直保持較高精度的穩定跟蹤，光照突變前后的跟蹤精度都高達99.56%，大大提高了MPPT 的穩定性，使算法在動態光照下也能穩定快速地跟蹤到最大功率點。

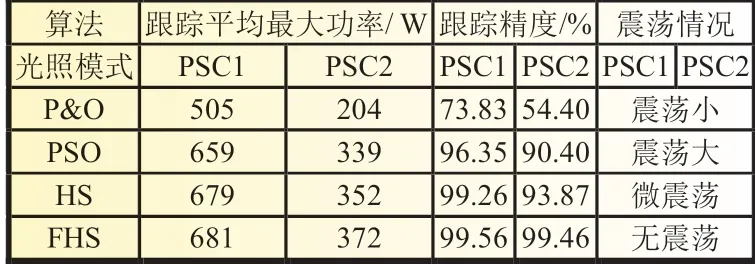
表3 動態仿真性能對比表

4 結論

本文通過把模糊控制的思想結合到和聲搜索算法MPPT中，引入模糊自適應因子k，提出了一種基于模糊和聲搜索(fuzzy harmony search，FHS)算法的光伏MPPT 控制方法，經過靜態和動態的仿真驗證表明，該算法能夠兼顧和聲搜索算法全局性強的優點，同時通過模糊自適應提高了算法的收斂速度，在非均勻光照下能夠保持較高的跟蹤精度，收斂速度快，功率震蕩小；在動態光照工況下也能快速、穩定、準確地搜索到全局最大功率點，為光伏MPPT 多峰值功率尋優提供了穩定有效的解決方案。