經管類微積分中一階微分方程的教學設計

◇上海立信會計金融學院統計與數學學院 楊 瑜 魏賀杰

本文將經典的SIR模型引入到經管類微積分的一階微分方程的教學內容中，并給出Matlab程序，對培養學生的好奇心和提高編程的能力有良好的效果。

1 引言

2020年9月11日習近平總書記在科學家座談會的講話中指出要把教育擺在更加重要位置，全面提高教育質量，注重培養學生創新意識和創新能力。筆者所在的學校是一所會計、金融特色鮮明的公辦全日制普通高等學校。每學年很多專業的學生要主修經管類的微積分課程，采用的教材是吳傳生教授編寫的《經濟數學-微積分(第三版)》。注意到教材中第十章第二節有關一階微分方程的平衡解及其穩定性的內容偏少而且不涉及編程方面的教學內容。2018年4月，教育部印發了《教育信息化2.0行動計劃》將信息技術納入初、高中學業水平考試。如何將高中數學與大學的微積分課程進行較好的銜接以及更好的培養學生的好奇心？這是一個非常值得去思考的問題。根據筆者多年的教學經驗，將自身的專業知識以及Matlab編程融入到教學中，這樣能更好的激發學生的學習興趣。本文將以SIR模型為教學切入點，介紹一階微分方程的相關概念并給出相應的Matlab程序。

2 教學案例設計

2020年9月8日在全國抗擊新冠肺炎疫情表彰大會上習近平總書記指出新冠肺炎疫情是百年來全球發生的最嚴重的傳染病大流行。為了讓學生理解傳染病的傳播規律以及如何科學的采取措施進行預防和控制，本文將經典的SIR模型融入到一階微分方程的教學中。

2.1 案例引入

傳染病動力學中經典的SIR模型[1]如下：

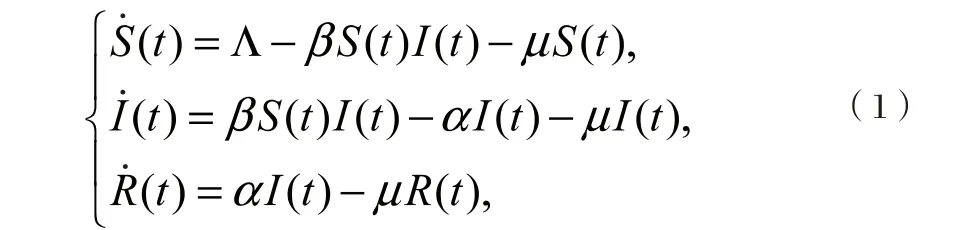
關于模型（1），我們重點考慮以下三個問題：(i) 它的平衡點有幾個？(ii) 它們的穩定性如何；(iii) 基本再生數與哪些參數有關。

2.2 案例分析

根據實際的意義，只在第一卦限對模型（1）進行討論。模型（1）的平衡點滿足

如下的代數方程組：

微分方程可用來描述物質的運動，而穩定性有明顯的物理意義。如果描述質點運動的微分方程的特解是不穩定的，那么初值的微小干擾將導致“差之毫厘，謬以千里”[7]。由文獻5知，當時，模型（1）只有無病平衡點且是全局漸近穩定的；當時，無病平衡點是不穩定的，而唯一的地方病平衡點是全局漸近穩定的。由基本再生數的表達式知，接觸率的減少或者感染者恢復率的增加將使其值減小。故傳染病暴發時，人們可以采取居家隔離、出門時佩戴口罩、注意個人衛生習慣及提高公共的衛生設施和醫療水平等措施切斷傳染病的傳播途徑，從而使傳染病更好的得到控制，緩解大眾的恐慌和焦慮情緒。

2.3 Matlab程序

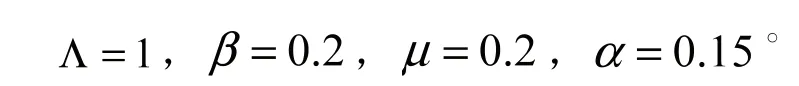
選取如下參數[8]：可得，故（1）的無病平衡點是不穩定的，唯一的地方病平衡點是全局漸近穩定的。

地方病平衡點穩定性的Matlab代碼如下：

2.4 知識延伸

現實生活中有些傳染病的發病具有明顯的季節性，如流感和登革熱；有些傳染病只針對某個年齡段的人群，如手足口病。因此，在建模過程中須考慮如周期、年齡和時滯等因素的影響。故原來的常微分方程就要變為相應的周期微分方程、年齡結構方程和時滯微分方程等來刻畫傳染病的傳播規律。

3 結束語

本文將專業知識融入到一階微分方程的教學內容中，培養了學生的創新思維和意識，提高了應用數學理論解決實際問題的能力。作為專業教師如何將專業的前沿知識更好的融入到教學中，我們的工作任重而道遠。