培養幾何直觀能力 提升學生數學素養
賈利冬 吳新穎

幾何直觀,主要指利用圖形描述和分析問題。借助幾何直觀,可以把復雜的數學問題變得簡明、形象,有助于學生探索解決問題的思路,培養數學思維,從而更深刻地理解數學知識。
1.梳理教材內容,構建宏觀框架
數學中的許多知識都是存在聯系的,由于難度不同,所以這些知識被安排在不同的年級。教師需要梳理教材內容,將存在聯系的知識點整合在一起,構建宏觀框架。
例如,在教“圖形的變換”時,教師讓學生思考,初一、初二學習的與圖形有關的數學知識都有哪些。通過回憶與翻閱資料,學生就能找到“相似形”“解直角三角形”“四邊形”“三角形”等相關的知識。隨后,教師可以引導學生從相似形的概念和繪圖方式等著手,構建出知識框架。學完這一章后,布置作業:以“圖形的變換”為中心詞畫思維導圖,并在課后展示、交流,進一步理解知識之間的聯系、區別,規律和本質。在這個過程中,學生不僅能夠全面了解圖形的知識,明白圖形之間存在的關聯,也能從不同知識點的解題技巧中逐漸培養幾何直觀能力。
2.營造幾何氛圍,將幾何直觀融入課堂教學
在教學中,教師應該學會將幾何直觀融入課堂教學的每一個環節,這樣,學生才能在長期熏陶中將其作為解決問題的首選方式,提升學習的效率。
一是在數學概念、定理、公理等的教學中滲透幾何直觀。數學概念、定理、公理都很嚴謹、抽象,理解起來有一定難度,可以讓學生借助圖形直觀感受,體會內涵。如在學習絕對值概念時,一定離不開數軸,教師可以讓學生在數軸上直觀感受兩點間的距離,理解絕對值的概念。
二是在發現結論的過程中引導學生直觀地思考。幾何直觀作為一種個體的感覺判斷能力,是需要在不斷的動手操作中去感受和體會的。課堂上,教師可以通過比一比、折一折、剪一剪、拼一拼、畫一畫等活動,讓學生在探究中獲得認知、感受和體會,驗證一些原有的猜想或者產生一些新的發現。比如,在學習“角邊角公理”時,讓學生在紙上畫一條長15cm的線段,以線段的兩個端點為頂點,在線段的同側做45°和60°兩個角,從而得到一個三角形,將這個三角形剪下來,讓同桌將兩個三角形放在一起,觀察是否重合。學生通過操作發現,這兩個三角形完全重合,也就是三角形全等,從而得到“角邊角公理”。
3.培養畫圖能力,發展幾何直觀能力
要讓學生具備用圖形解決問題的能力,教師還需要培養學生的畫圖能力。
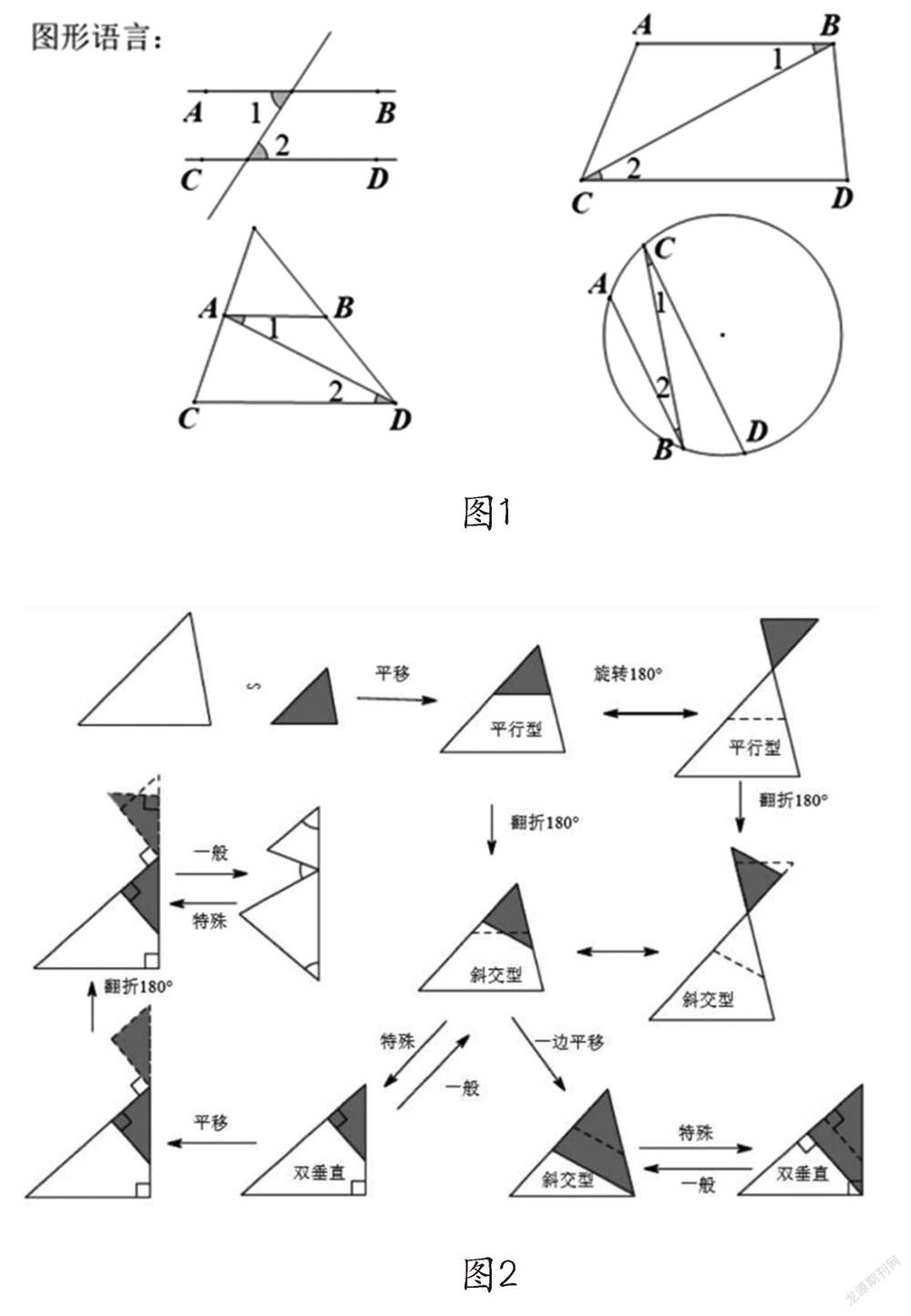
一是訓練三種數學語言的相互轉化。幾何語言的基本形式有文字語言、圖形語言和符號語言三種。由于三種語言的特點不同,在幾何教學中所發揮的作用也不同。在教學中,反復訓練這三種語言的轉化,形成技能,可以為后續的幾何學習打下堅實基礎。特別是圖形語言,它可以有各種變化(如圖1)。
二是積累基本圖形,加強幾何直觀能力培養。看到一個幾何數學問題時,如果能夠快速通過觀察、發現、分析,分離出圖形中的基本圖形,對解決數學問題可以起到事半功倍的效果。培養這樣的幾何直觀能力,需要學生平時加強對基本圖形的學習和積累。教師在課上、課下要引導學生多觀察、多總結。例如,學習相似三角形后,教師可以讓學生自己總結相似的基本圖形(如圖2),學生積累了一定的基本圖形后,就可以在復雜圖形中快速發現基本圖形,問題解決起來也就很容易了。
4.聯系實際生活,深化幾何直觀能力
培養學生的幾何直觀能力,不僅是為了提升學生的數學素養,更是為了讓學生將這一思想運用于實際生活中。因此,在幾何直觀能力的培養中,教師需要為學生創設生活情境,將生活案例引入課堂教學,提高教學效率,讓學生更好地理解數學與生活的關系。
例如,讓學生測量跳遠成績,感受數學中點到直線的距離;通過觀察教室里的物品,得出兩條直線的位置關系;觀察太陽光下的影子、路燈下的影子,尋找一個物體和它的投影之間的關系等。通過生活實際的積累,增強學生對數學知識的感性認識,而這些概念經過“直觀”后,也讓學生得到了很好的理解。
綜上所述,培養學生的幾何直觀能力,不僅有助于提升學生的數學水平,還可以培養學生的空間思維和理性思維,為學生的未來發展奠定良好的基礎。因此,教師需要梳理教學內容,營造幾何氛圍,開展實踐教學,聯系實際生活,讓學生學會用圖形“說話”、用圖形描述問題、用圖形討論問題以及用圖形解決問題。
本文系北京市教育科學“十三五”規劃課題“提升畫圖能力,發展幾何直觀——以平谷區農村地區初中生為例”(課題編號:CDDB18319)結題成果
編輯 _ 汪倩

