半環的范德瓦爾登問題

茍旭,邵勇

(西北大學數學學院,陜西 西安 710127)

1 引言及預備知識

環是否可以嵌入到域的問題,一經提出就引起了不少學者的關注.文獻[1]構造了整環的分式域,并證明任意整環都可嵌入其分式域.文獻[2]提出無零因子非交換環是否可以嵌入到Skew域中的問題,將上述問題稱為范德瓦爾登問題.文獻[3]證明了正則環可以嵌入到Skew域,一定程度上解答了范德瓦爾登問題.

不難發現,整環的非零元在乘法下構成交換半群,而域的非零元在乘法下構成阿貝爾群.既然整環可以嵌入其分式域,那么整環的非零元在乘法下構成的交換半群可嵌入其分式域的非零元在乘法下構成的群.隨著半群代數理論的不斷發展,半群的嵌入問題也引起了學者們的關注.一般而言,交換半群可以構造其對應的格羅滕迪克群(Grothendieck group)[4].進而,可以證明可消交換半群可以嵌入其格羅滕迪克群.文獻[5]給出了拓撲半群嵌入緊拓撲群的刻畫.文獻[6]給出了局部半群嵌入群的充分條件.

作為環的推廣,半環是分配律聯系著的同一非空集合上的兩個半群.半環的具體定義如下:

定義 1.1設(S,+,·)是 (2,2)-型代數.若滿足下列條件:

(1)(S,+)是交換半群;

(2)(S,·) 是半群;

(3)左右分配律成立,即 (?a,b,c∈S)a·(b+c)=a·b+a·c,(b+c)·a=b·a+c·a,則稱 (S,+,·)是半環[7],簡記 S.若 (S,·)是交換半群,則稱 S是交換半環.若 S滿足(?a,b,c∈S)a+b=a+c?b=c,則稱S是加法可消的.容易驗證,有限的加法可消半環是環.

半環的嵌入問題同樣吸引了不少學者關注.文獻[8]證明了含幺含零加法可消半環可嵌入環.然而,正整數在通常數的加法和乘法下構成半環(不含零元),并且可以嵌入整數環中.這表明某些不含零元的半環也可以嵌入環中.本文將給出半環的格羅滕迪克環的構造方法,并證明加法可消半環可嵌入其格羅滕迪克環.進一步揭示了半環上的同余和其格羅滕迪克環的理想之間的關系.

定義 1.2設S是半環.在卡氏積 S×S上定義運算如下:

(a,b)?(c,d)=(ac+bd,ad+bc).

稱?為 S×S上的扭積[9].

設(S,+)是交換半群,在S×S上定義關系～如下:

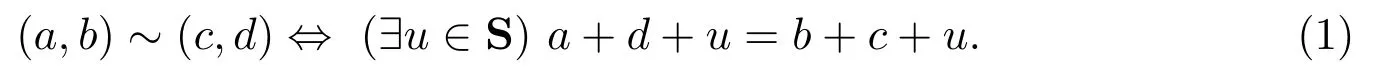
容易驗證,～是 S×S上的等價關系.

對任意的(a,b),(c,d),(e,f)∈S×S,若 (a,b)～(c,d),則存在u∈S使得

a+d+u=b+c+u.

上式兩邊加上e+f有a+d+u+e+f=b+c+u+e+f.由 (S,+)是交換的可得(a+e)+(d+f)+u=(b+f)+(c+e)+u,即(a+e,b+f)～(c+e,d+f).于是,(a,b)+(e,f)～(c,d)+(e,f).從而,～是直積 S×S上的同余.則(S×S/～,+)是交換半群.記(a,b)所在的～類為

2 半群觀點下的整環的分式域

整環的分式域理論是代數理論的重要部分,是構造域的重要方法.本節將從半群角度解釋整環的分式域過程.

設 R是整環,記R?=R{0},其中0是R的零元.在R×R?上定義

(a,b)+(c,d)=(ad+bc,bd),(a,b)·(c,d)=(ac,bd),

易知(R×R?,+),(R×R?,·)均是交換幺半群.

在 R×R?上定義 ～關系 (a,b)～(c,d)??ad=bc.由文獻 [10]可知 ～是R×R?上的等價關系.

下證 ～ 是 (R×R?,+)和 (R×R?,·)上的同余.

對任意的(a,b),(c,d),(e,f)∈R×R?,若(a,b)～(c,d),則ad=bc.上式左右同乘ff有adff=bcff.進一步有adff+bdef=bcff+bdef,即

(af+be)df=(cf+de)bf.

這樣(af+be,bf)～(cf+de,df),即(a,b)+(e,f)～(c,d)+(e,f).從而,～是(R×R?,+)上的同余.

同理,ad=bc左右同乘ef有adef=bcef,故(ae,bf)～(ce,df),即

由文獻[10]可知,(R×R?/～,+,·)中+對·分配律成立.所以 (R×R?/～,+,·)是域.

3 主要結果

本節將證明任意加法可消半環可嵌入其格羅滕迪克環中.

設S是半環.在S×S上定義+,?如下:

(1)(a,b)+(c,d)=(a+c,b+d);

(2)(a,b)?(c,d)=(ac+bd,ad+bc).

由文獻[8]可知,(S×S,+,?)是半環.

在S×S上定義關系～如下:

(a,b)～ (c,d)?(?u∈S)a+d+u=b+c+u.

由(1)式可知,～是(S×S,+)上的同余.

下證 ～ 是 (S×S,?)上的同余.設(a,b),(c,d),(e,f)∈S×S,若 (a,b)～(c,d),則

存在u∈S使得

(2)式兩邊右乘e

(2)式兩邊右乘f

(3)式和(4)式相加可得

于是,(ae+bf,af+be)～ (ce+df,cf+de).既然 (a,b)?(e,f)=(ae+bf,af+be),(c,d)?(e,f)=(ce+df,cf+de),從而,(a,b)?(e,f)～ (c,d)?(e,f).這表明 ～ 是 (S×S,?)的右同余.同理可證,～是(S×S,?)上的左同余.所以 ～是(S×S,?)上的同余.因此,～是 (S×S,+,?)上的同余.記(a,b)所在的 ～類為