一類平坦半環生成的簇

高子東,任苗苗

(西北大學數學學院,陜西 西安 710127)

1 引言和預備知識

設 V是同型代數作成的類.若 V對子代數,直積和同態像封閉,則稱其為簇.由Birkhoff定理可知,一個同型代數類是簇當且僅當它是等式類,即滿足某個恒等式集合的代數的全體.若簇V可由有限個恒等式確定,則稱V是有限基底的,否則稱V為非有限基底的.簇的有限基底問題是問它是否為有限基底的,該問題是簇的核心問題之一.設K是一些同型代數作成的類,用V(K)表示由K生成的簇,即包含K的最小的簇.若K中只有一個成員A,則簡記為V(A).由Tarski定理可知,V(K)=HSP(K),其中H,S,P分別是同態像,子代數和直積類算子.

設(Ai)i∈I是一族同型代數,A是的子代數.若對于任意j∈I,用

表示自然投射,均有πj(A)=Aj,則稱A是 (Ai)i∈I的次直積.如果代數A只有平凡的次直積分解,即對于任意一族同型代數 (Ai)i∈I,A是 (Ai)i∈I的次直積蘊含著存在i∈I,使得AAi,則A被稱為次直不可約的.若A是非平凡的代數,則A是次直不可約的當且僅當它有最小的非平凡同余.由文獻[1]知,簇V的每個成員都可表示為它的一些次直不可約成員的次直積.這表明簇V完全被它的次直不可約成員所確定.因此,研究簇的次直不可約成員是簇的又一核心問題之一.

定義 1.1[2]設S是半群,A是S的任一非空子集.若AA?A,則稱A為S的子半群,記作A≤S.若AS,SA?A,則稱A為S的理想,記作AS.

設I是半群S的理想.則ρI(I×I)∪1S稱為S上(由I確定)的Ress同余[3].其對應的商半群為

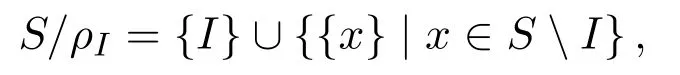
簡記為S/I.容易驗證,I是商半群S/I的零元,因此也可將S/I視為(SI)∪{0}.反之,則有如下命題:

命題1.1設S是含0的半群.若S上有同余ρ=(0/ρ×0/ρ)∪1S,則I0/ρS,進而ρ=ρI是半群S上的Ress同余.

證明設a∈0/ρ,s∈S.由aρ0,sρs,且ρ是S上的同余,可得

asρ0s=0,saρs0=0.

也即as,sa∈0/ρ.這表明I0/ρS,進而ρ=ρI是半群S上的Ress同余.

定義 1.2[2]設S是含0的半群.若對于任意a∈S,存在n∈N,使得an=0,則稱S為nil-半群.

下面將給出nil-半群的0-極小理想[2]的刻畫:

命題 1.2設S是nil-半群.若I是S的0-極小理想,則|I|=2.

證明任取a,b∈I{0}.由I的 0-極小性可知,S1aS1=S1bS1.故存在x,y,u,v∈S1,使得b=xay,a=ubv.因此

a=(ux)a(yb)= ···(ux)na(yb)n= ···.

結合S是nil-半群以及a0可知,x=y=u=v=1.這表明a=b.故|I|=2.

定義 1.3[2]設S是含0的半群.若滿足:

則稱S為0-可消半群.

在下一節中,將討論0-可消半群與平坦半環的關系.下面介紹半環的一些基本概念:

定義 1.4[2]設 (S,+,·)是(2,2)型代數.若滿足:

(1)(S,+),(S,·) 是半群;

(2)(a+b)c=ac+bc,c(a+b)=ca+cb,?a,b,c∈S,則稱 (S,+,·)為半環,簡記為S.

若半環S滿足

a+b=b+a,a+a=a,?a,b∈S,

則稱S為加法冪等元半環,簡記為ai-半環.

對于ai-半環S,定義偏序關系如下:

(?a,b∈S)a≤b?a+b=b.

容易驗證,(S,≤)是(上)半格,因此ai-半環也被稱作半格序半群.

定義 1.5[3]設S是半環,A是S的任一非空子集.若A≤(S,+)且A≤(S,·),則稱A是S的子半環,記作A≤S.若A(S,+)且A(S,·),則稱A是S的理想,記作AS.

近二十年來,ai-半環簇的研究是非常活躍的[3-15].文獻[11-12]研究了x2≈x確定的ai-半環簇.文獻[3]給出了第一個非有限基底的有限ai-半環的例子.文獻[5]給出了恒等式xn≈xm確定的ai-半環簇的自由對象的模型.文獻[6]證明了若ai-半環滿足恒等式xn≈x,則它的乘法導出是正則純正密碼群.文獻[7-8]證明了滿足恒等式x3≈x的ai-半環簇共有179個,且這些簇都是有限基底的.文獻[10]研究了所有二階ai-半環生成的簇,證明了它的子簇格是64階的布爾代數.文獻[13]研究了三階ai-半環的有限基底問題.在上述文獻的基礎上,本文將主要研究次直不可約的平坦半環,以及一類平坦半環生成的簇.給出次直不可約的nil-平坦半環的一些等價刻畫,證明當n≤3時,平坦半環S(x1x2···xn)均是有限基底的.

2 次直不可約的 nil-平坦半環

定義 2.1[1]設S是含乘法零元的半環.若其加法導出(S,+)滿足:

則稱S是平坦半環.

為了方便起見,將上述的“加法”稱為 flat加法.容易驗證,平坦半環S是一類特殊的ai-半環,其乘法零元亦是加法零元,且當|S|≥2時,(S,≤)是高度為1的半格.下面的引理將說明平坦半環與0-可消半群之間的關系:

引理 2.1設S是平坦半環,則其乘法導出 (S,·)是 0-可消半群.反之,對于任一0-可消半群(S,·),都可以定義 flat加法,使得(S,+,·)成為平坦半環.

證明設S是平坦半環.任取a,b,c∈S,若ab=ac0,則ab+ac=a(b+c)0,因此b+c0,故b=c.同理可知,由ba=ca0亦可推出b=c.因而,(S,·)是 0-可消半群.

反之,設 (S,·)是 0-可消半群,定義上述 flat加法.下面只需驗證乘法 “·”對加法“+”具有左右分配律即可.任取a,b,c∈S:

(i)若b=c,則a(b+c)=ab=ab+ac.

(ii)若bc,則a(b+c)=a0=0.斷言ab+ab=0,否則ab+ac0,進而ab=ac0,再由S的0-可消性可知,b=c,矛盾.因此,a(b+c)=0=ab+ac.

綜上所述,a(b+c)=ab+ac.同理可知,(b+c)a=0=ba+ca.因此,(S,+,·)是平坦半環.

上述引理說明,平坦半環與0-可消半群具有一一對應的關系.因此構造具體的平坦半環時,只需構造出0-可消半群,然后在此基礎上賦予 flat加法即可.容易驗證,對于任意可消半群S(或更為特殊的自由半群,群等),直接添加零元,即可得到0-可消半群S0.但這并不意味著0-可消半群都是通過這種方式得到的,例如null-半群S(也即滿足S2={0}的半群).下面將介紹一類重要的0-可消半群:

命題 2.1設W是自由半群X+的任一非空子集.令

則 (S(W),·)是 0-可消半群.

證明直接驗證可知,(S(W),·)滿足結合律以及 0-可消性.為了揭示 (S(W)與X+0的關系,取I=X+S(W),則有IX+0且X+0/I～=S(W).而X+0是 0-可消的,進而容易驗證X+0/I亦為0-可消半群,因此S(W)也是0-可消半群.

賦予 flat加法可知,(S(W),+,·)是平坦半環,簡記為S(W).當W={w}為單點集時,也可將S({w})簡記為S(w).下一節將重點討論S(w)的相關問題.在此之前,首先說明平坦半環的子半環與商半環的特點以及證明平坦半環上的同余恰為Ress同余.

命題 2.2設S為平坦半環,則有如下結論成立:

(1)S的任一子半環T均為平坦半環,其中子半環T按(2,2,0)型代數考慮,也即T需含有S中的零元;

(2)S的任一商半環S/ρ均為平坦半環;

(3)設A是S的任一非空子集,則

〈A〉={a1a2···an|ai∈S,i=1,···,n,n∈N}∪{0}.

其中〈A〉表示S中由子集A生成的子半環,也即S中包含A的最小子半環;

(4)設A是S的任一非空子集,則S1AS1是S中包含子集A的最小理想.

證明(1)設T為S的任一子半環.由引理2.1可知,只需驗證(T,·)為0-可消半群即可.由于S中的零元在T中,從而亦是T的零元,因此結論顯然成立.

(2)由引理2.1可知,只需驗證(S/ρ,·)為0-可消半群即可.任取若,則有.由引理2.2可知,因此,ab=ac0.結合S的0-可消性可知,b=c,也即=.同理可知,由亦可推出=.故(S/ρ,·)為0-可消半群,結論得證.

(3)記等式右邊的集合為B.若T是包含A的任一子半環,則有B?T.因此只需證明B是子半環即可.易知B≤(S,·).由0∈S結合 flat加法的性質可得,B≤(S,+).因此B是S的子半環,結論得證.

(4)類比(3)證明可知,結論顯然成立.

引理 2.2設S為平坦半環.若ρ為(S,+)上的同余,則有

ρ=(0/ρ×0/ρ)∪1S=ρI,

其中I=0/ρ是 (S,+)上的理想.反之,若I是S是任一含 0的非空子集,則有I(S,+).

證明令ρ為(S,+)上的同余.任取a,b∈S且ab.若aρb,則有

a=a+aρa+b=0,b=b+bρa+b=0.

因此a,b∈0/ρ,即有ρ=(0/ρ×0/ρ)∪1S.再由命題 1.1可知,I=0/ρ是 (S,+)上的理想,進而ρ=ρI.

反之,若I是S是任一含0的非空子集,則有I+S=S+I=I.由定義可知,I(S,+).

上述引理表明(S,+)上的同余恰為Ress同余,而(S,+)上的理想也恰為S的某一含0的非空子集,且二者具有一一對應的關系.進而有如下命題:

命題 2.3設S為平坦半環,ρ?S×S.則ρ是S上的同余,當且僅當存在I(S,·),使得ρ=ρI.

證明充分性.若存在I(S,·),使得ρ=ρI,則ρI是 (S,·)上的同余.而I是含 0的非空子集,由引理 2.2可知,I(S,+).因此,ρI也是 (S,+)上的同余,進而ρ=ρI是S上的同余.

必要性.若ρ是S上的同余,則ρ是其加法導出(S,+)上的同余.故由引理2.2可知,ρ=(0/ρ×0/ρ)∪1S=ρ0/ρ.結合ρ亦是其乘法導出 (S,·)上的同余,由命題 1.1可知,0/ρ(S,·).這表明ρ=ρI,其中I0/ρ(S,·).

由上述命題可知,平坦半環上的同余均為Ress同余,且與乘法導出的理想具有一一對應的保序關系.進而有如下推論:

推論 2.1設S是非平凡的平坦半環.則S是次直不可約的,當且僅當(S,·)有唯一的0-極小理想.

定義 2.2設S是半環.若 (S,·)是 nil-半群,則稱S為nil-半環.

定義 2.3[2]設S是平坦半環.若存在ω∈S{0},使得Sω=ωS={0},則稱ω是S的零化子.

命題 2.4設S是非平凡的nil-平坦半環.則S是次直不可約的,當且僅當S有唯一的零化子ω.

證明必要性.由于S是次直不可約的,由推論2.1可知,(S,·)有唯一的0-極小理想I.而 (S,·)是 nil-半群,結合命題 1.2可知 |I|=2,不妨記為I={0,ω}.由理想的定義可知,任取s∈S,sω∈I.若sω=ω,則

ω=sω=s2ω=s3ω= ···,

而 (S,·)是 nil-半群,故ω=0,矛盾.因此,sω=0.同理可知ωs=0,從而ω是S的零化子.下證唯一性,設ω′是S的任一零化子.則{0,ω′}是 (S,·)的 0-極小理想.由 0-極小理想的唯一性可知,{0,ω′}={0,ω}.因此,ω′=ω.

充分性.若S有唯一的零化子ω,則I?{0,ω}是 (S,·)的 0-極小理想.欲證S是次直不可約的,由推論 2.1可知,只需說明 (S,·)有唯一的 0-極小理想即可.設J為(S,·)的一個0-極小理想.由命題1.2可知,|J|=2.不妨設J={0,a}.由必要性證明可知,a是S的一個零化子.結合S有唯一的零化子可知,a=ω.因此,I=J.

若取W為自由半群X+的有限非空子集,則有S(W)是一個有限的nil-平坦半環,且W中的極大字恰為S(W)的零化子.因此,有如下推論:

推論 2.2設W為自由半群X+的有限非空子集.則下列命題等價:

(1)S(W)是次直不可約的;

(2)W中有唯一的極大字;

(3)存在w∈W,使得S(W)=S(w).

3 一類平坦半環生成的簇

從上一節可知,平坦半環是特殊的ai-半環,且關于子代數和商代數封閉.但平坦半環的直積未必是平坦半環,因此所有的平坦半環作成的類并不是一個簇,進而考慮由所有的平坦半環生成的簇,記作F.顯然F是ai-半環簇AI的子簇.結合文獻[4]可得下列兩個引理:

引理 3.1F是由ai-半環簇AI填加下列恒等式所確定的簇:

a(x+y)b+c(x+y)d≈a(x+y)b+cxd.

其中,a,b,c,d中的任意一個均可為空.

引理3.2F中的次直不可約成員必為平坦半環.

接下來將主要討論V(S(x1x2···xn))的有限基問題.首先,記Vn(n∈N)為F添加如下恒等式確定的簇:

其中,v∈{x1,x2,···,xk}+且vx1x2···xk;在 (5)式中,a,b中至少有一個為空;在(6)-(8)式中,a,b中任意一個均可為空.

顯然S(x1x2···xn)滿足上述恒等式,因此 V(S(x1x2···xn))?Vn,n∈N.下面將證明n=1,2,3時,V(S(x1x2···xn))=Vn.在此之前,先說明 Vn中次直不可約成員的一些基本性質:

引理 3.3設S是Vn中任一非平凡次直不可約成員.則有如下結論成立:

(1)S是平坦半環,它有唯一的零化子ω,進而{0,ω}是S的唯一0-極小理想;

(2)若存在k∈N,使得Sk={0}且Sk+1{0},則Sk={0,ω};

(3) 若存在b1,b2,···,bn,c1,c2,···,cn∈S, 使得b1b2···bn=c1c2···cn=ω,則有bi=ci,1≤i≤n;

(4) 若存在a1,a2,···,am∈S使得a1a2···am0,則

〈a1,a2,···,am〉=S(x1x2···xm),

其中〈a1,a2,···,am〉表示由{a1,a2,···,am}生成的子半環.

證明(1)由于S是Vn中的次直不可約成員,進而亦是F中的次直不可約成員.故由引理3.2可知,S是平坦半環.根據恒等式(2)可知,(S,·)是nil-半群,于是S是次直不可約nil-平坦半環.結合命題2.4可知,S有唯一的零化子ω.進而,{0,ω}是S的唯一0-極小理想.

(2)若存在k∈N,使得Sk{0}且Sk+1={0}.任取s=s1s2···sk∈Sk且s0.由于I是S的 0-極小理想,因而I?S1sS1.故存在u,v∈S1,使得ω=usv=us1s2···skv.結合Sk+1={0}可知,u=v=1,也即s=ω.這表明Sk={0,ω}.

(3)由恒等式(3)可知,結論顯然成立.

(4)根據命題2.2(3)可知,只需證明:

〈a1,a2,···,am〉={aiai+1···aj|1≤i≤j≤m}∪{0}.

記等式右邊的集合為A.顯然A?〈a1,a2,···,am〉,所以只需說明〈a1,a2,···,am〉?A,且A中元素互不相同即可.任取v∈{a1,a2,···,am}+且va1a2···am.斷言v=0,否則根據ω∈S1vS1可知,存在a,b∈S1使得ω=avb.進而a1a2···am+avb=0,這與恒等式 (6)矛盾,于是〈a1,a2,···,am〉=A.若A中有兩個元素相同,不妨設aiai+1···aj=akak+1···a?,其中 1≤i≤j,k≤?.下面分兩種情形討論:

(i)若j≤k,則利用恒等式(1)和恒等式(4)可知,任取a,b∈S,總有a2=aba=0.因此得到a1a2···am=0,矛盾.

(ii) 若j>k,記ai···ak=x,ak+1···aj=y,aj+1···a?=z,則有xy=yz0,于是xy+yz0,這與恒等式(2)矛盾.

綜上所述,〈a1,a2,···,am〉=S(x1x2···xm).

由恒等式(1)得,Vn,V(S(x1x2···xn))均為局部有限簇.再結合

V(S(x1x2···xn))?Vn

可知,只需證 Vn中任一 (有限)非平凡次直不可約成員,均落在 V(S(x1x2···xn))即可.

定理3.1V(S(x1))=V1.

證明任取V1中的非平凡次直不可約成員S.由引理3.3(1)可知,S是次直不可約的平坦半環,且有唯一的0-極小理想{0,ω}.結合恒等式(1)可知,S2={0},從而(S,·)為 null-半群.因此S的任一含0非空子集均為S的理想.結合0-極小理想的唯一性可知,S={0,ω}S(x1)∈V(S(x1)).

定理3.2V(S(x1x2))=V2.

證明任取V2中的非平凡次直不可約成員S.由引理3.3(1)可知,S是次直不可約的平坦半環,且有唯一的0-極小理想{0,ω}.結合恒等式(1)可知,S3={0}.因此,分下列兩種情形討論:

(i)S2={0}.由定理 3.1可知,SS(x1)∈V(S(x1x2)).

(ii)S2{0}.由引理 3.3(2)可知,S2={0,ω}.于是存在x1,x2∈S,使得x1x2=ω0.由引理 3.3(4)可知,〈x1,x2〉=S(x1x2).斷言S=S(x1x2),否則存在e∈SS(x1x2).結合ω∈S1eS1可知,存在a,b∈S1,使得ω=aeb.結合S3={0}且eω可知,a=1,b∈S或b=1,a∈S.再由引理3.3(3)可知,e=x1,b=x2或a=x1,e=x2,這與e∈SS(x1x2)矛盾.因此S=S(x1x2)∈V(S(x1x2)).

為了更好的刻畫Vn,接下來引入“0-ω直并”的概念.進而說明V(S(x1x2···xn))中具有一類非常“典型”的次直不可約成員.

設 (Si)i∈I是一族次直不可約的 nil-平坦半環,且滿足Si∩Sj={0,ω},i,j∈I且ij,其中,ω是Si(i∈I)的唯一零化子.令.任取a,b∈S,定義