雙滾輪-導軌式漸開線測量儀的空間幾何誤差補償方法

凌四營，孔玉梅，趙昌明，凌 明，王立鼎1，

（1.大連理工大學 精密特種加工教育部重點實驗室，遼寧 大連116024；2.大連理工大學 微納米技術及系統遼寧省重點實驗室，遼寧 大連116024）

1 引 言

齒輪是量大面廣的關鍵基礎零部件，隨著科學技術的不斷發展，人們對齒輪精度的要求也越來越高。齒輪樣板是一類用于齒輪量值傳遞基準與精度溯源的標準器件，包括齒輪漸開線樣板、齒輪螺旋線樣板和齒距樣板等，其制造水平是一個國家齒輪技術實力的重要標志之一。其中，齒輪漸開線樣板是校準各種漸開線測量儀器的標準計量器具，主要用于傳遞齒輪漸開線參數量值、修正儀器示值和確定儀器示值誤差［1］。

我國有獨立的齒輪漸開線樣板國家標準GB/T 6467-2010［2］，并定義了兩個等級的齒輪漸開線樣板，其中規定基圓半徑rb≤100 mm的1級齒輪漸開線樣板的齒廓形狀公差不大于1μm。與同等基圓參數的1級精度標準圓柱齒輪相比，1級精度齒輪漸開線樣板的展開長度擴大了約80%，而齒廓形狀公差縮小了約40%。因此，1級精度齒輪漸開線樣板的測量難度更高。目前商品漸開線測量儀器的測量不確定度都達不到1級漸開線的測量要求。因此，開展1級齒輪漸開線樣板測量技術的研究具有重要意義。

齒廓偏差是齒輪精度評估的重要指標之一［2-3］，在諸多測量漸開線齒廓偏差的測量儀器中，以齒輪測量中心（Gear Measuring Center，GMC）和三坐標測量機（Coordinate Measuring Machine，CMM）應用最為廣泛［4］。對儀器的誤差進行補償是提升齒輪測量儀器的測量精度的常用技術手段。齒輪測量儀器的誤差來源可分為系統誤差和隨機誤差，其中系統誤差主要包括空間幾何誤差、測頭系統誤差和測量方法誤差等［5-7］。GMC和CMM的集成化程度高、功能強大、測量精度較高，但測量尺寸鏈長，精度提升空間有限，不滿足1級齒輪漸開線樣板的測量要求；國內外對兩種儀器的精度提升研究已持續了幾十年，主要從幾何誤差、數據處理軟件優化、傳感器精度、伺服路徑規劃和角度分度等方面提升精度［8-14］。

對比上述齒輪測量儀器，基于機械展成原理的雙滾輪-導軌式漸開線測量儀結構更簡單，尺寸鏈短，精度容易得到保證。滾輪-導軌式展成機構也是國內外普遍認可的具有最高展成精度的機構，該機構一般用于漸開線的精密測量領域［15］。對于該儀器，空間幾何誤差是其主要誤差來源，包括驅動軸的位置誤差、基圓盤及導軌的制造誤差和各零件之間的安裝誤差等。一方面，關鍵零部件存在制造誤差，且到某一公差后減小空間有限；另一方面操作人員會帶來安裝誤差（如偏心、偏擺誤差）。因此，探索出一種能夠精確表征空間幾何誤差與齒廓偏差映射關系的測量方法，即利用零件的制造誤差與安裝誤差互相抵消的補償方法，對于漸開線測量精度的提升顯得尤為重要。

針對雙滾輪-導軌式漸開線測量儀，文獻［16］分析了由基圓盤半徑偏差引起的測量誤差；文獻［17］對基圓盤滾動精度展開了研究，并分析對比了不同的驅動方式對測量結果的影響；文獻［18］分析了測量點偏差引起的測量誤差；文獻［19］分析了齒輪安裝偏心對漸開線齒廓傾斜偏差的影響。以上文獻都是針對儀器中的某一項誤差源展開分析，對于其他誤差源不具有普適性。文獻［15］對儀器測量過程中的大多數誤差源展開分析，補償掉部分誤差后儀器的測量不確定度可達0.31μm，但被測齒輪的展開長度較短，按照齒廓形狀偏差的測量不確定度應不大于齒廓形狀偏差最大允許公差的1/3的要求［20］，該儀器仍然不滿足1級精度齒輪漸開線樣板的測量要求。

為了提升雙滾輪-導軌式漸開線測量儀的精度，本文提出了一種空間幾何誤差補償新方法，并基于該方法分析了基圓盤、齒輪漸開線樣板與芯軸的綜合安裝誤差和基圓盤的圓度誤差對測量結果的影響，探索出裝配誤差和關鍵零部件的制造誤差相互抵消的補償方法，最后設計測量實驗驗證了空間幾何誤差補償方法的有效性。

2 漸開線測量儀工作原理與齒廓偏差補償模型

2.1 雙滾輪-導軌式漸開線測量儀工作原理

雙滾輪-導軌式漸開線測量儀的工作原理如圖1所示，圖中的滾輪由兩個基圓盤組成，基圓盤與齒輪漸開線樣板的基圓半徑相同且同軸連接，當基圓盤在導軌上做純滾動運動時，理論上漸開線與導軌平面的交點（即測量點）保持不動且該點在漸開線上的法線與基圓相切。實際的漸開線并不是一條理想的漸開線，故在實際測量過程中，測量點在水平方向上會產生偏移，該偏移量即表征被測漸開線的齒廓偏差。

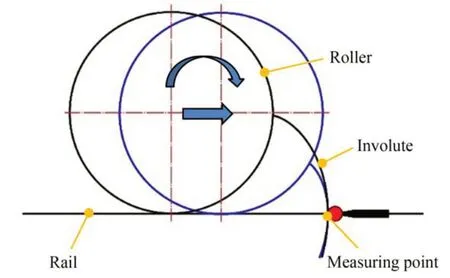
圖1 雙滾輪-導軌式漸開線測量儀的工作原理Fig.1 Working principle of double roller-rail involute measuring instrument

雙滾輪-導軌式漸開線測量儀的測量過程如下：將純滾動組件（如圖2所示，由兩個基圓盤、齒輪漸開線樣板和芯軸等組成）放置到導軌上，并緊貼于基圓盤定位擋板以校正滾動方向；調整測頭測量方向與導軌平行并使測量點位于導軌平面內；驅動裝置帶動純滾動組件沿著水平方向滾動的同時，數據采集系統開始實時采集被測漸開線的齒形信息，最后根據采集的數據計算出被測漸開線的齒廓偏差。

圖2 純滾動組件Fig.2 Pure rolling component

該測量方法的精度很大程度上依賴于展成機構的展成精度，其中基圓盤是展成機構中的最關鍵零件，它的制造誤差和裝配誤差是影響測量精度的主要誤差源。此外，測點的位置誤差、導軌的平面度誤差、兩條導軌之間的平行度誤差、齒輪漸開線樣板與芯軸的裝配誤差等也會影響測量結果。

2.2 齒廓偏差補償模型的建立

齒廓偏差補償模型旨在建立原始誤差、機構和運動參數與齒廓偏差之間的數學關系，是空間幾何誤差分析的理論基礎和關鍵，通過模型建立的數學關系，修正儀器的示值誤差，提高漸開線齒廓偏差的測量精度。

為此，先建立兩個空間坐標系：儀器坐標系OwXwYwZw和工件坐標系ObXbYbZb。OwXwYwZw坐標系中的坐標原點Ow為理想狀態下測量點初始所在位置，Xw軸指向導軌的延伸方向，Yw軸指向平行于芯軸軸線方向，Zw軸指向豎直方向。ObXbYbZb坐標系中的坐標原點Ob為被測樣板的中心，Xb軸指向被測樣板中漸開線起始點與樣板中心的連線方向，Yb軸指向芯軸軸線方向，Zb軸指向同時垂直于Xb軸和Yb軸的方向，如圖3所示。

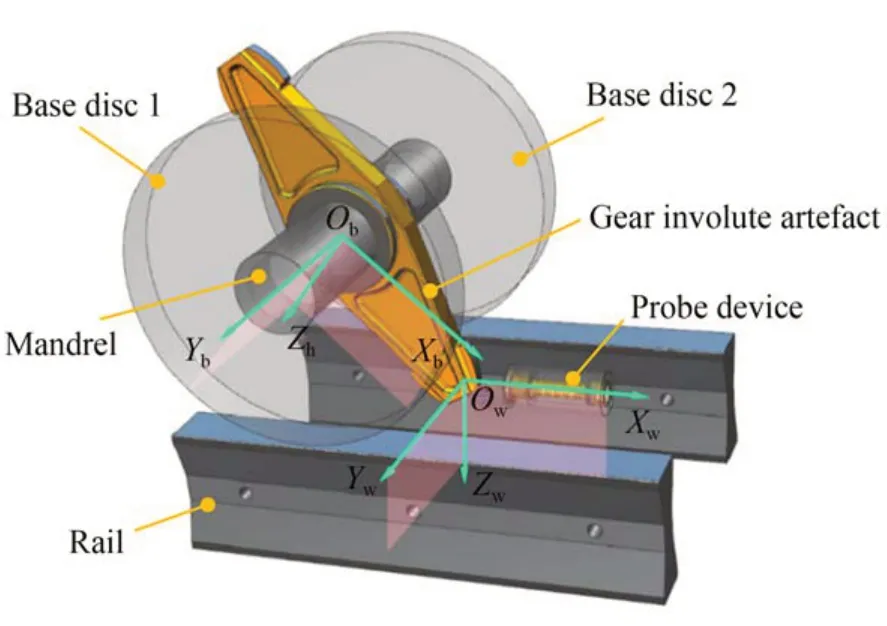
圖3 儀器坐標系與工件坐標系示意圖Fig.3 Diagram of the machine coordinate system and the workpiece coordinate system

儀器坐標系的位置是固定的，而工件坐標系的位置隨著基圓盤的滾動不斷發生變化，工件坐標系相對于儀器坐標系有6個自由度，故存在6個空間幾何誤差，如圖4所示，分別為3個線性誤差ex、ey、ez和3個旋轉誤差r x（ObXbYbZb坐標系繞Xw軸的旋轉角）、r y（ObXbYbZb坐標系繞Yw軸的旋轉角）、rz（ObXbYbZb坐標系繞Zw軸的旋轉角）。其測量原理是計算出實際測量過程中測球與漸開線接觸點與理論接觸點在儀器坐標系OwXwYwZw中的Xw軸坐標之差Δ。

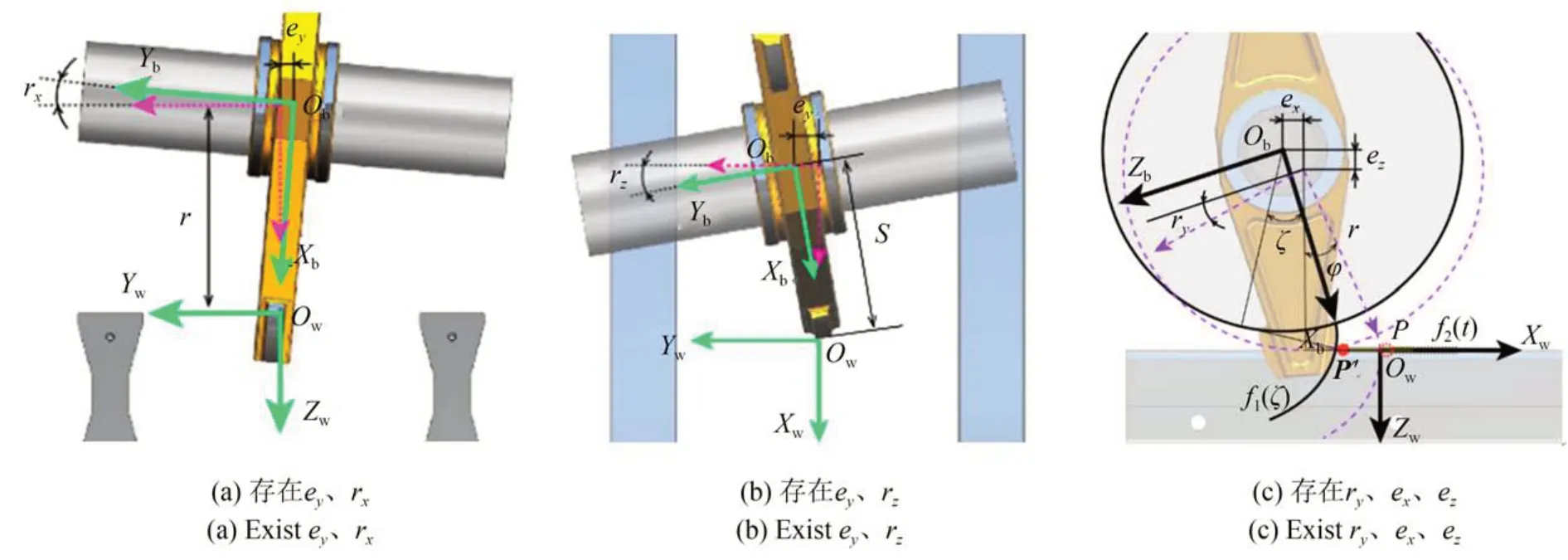
圖4 空間幾何誤差引起測量誤差的原理Fig.4 Principle of measurement error caused by spatial geometric errors

2個線性誤差ex、ez和3個旋轉誤差r x、ry、r z都會導致測量點產生偏移。ey單獨出現時對測量不產生影響，當ey與r x或r z同時出現時便會對測量結果產生影響。若被測樣板存在線性誤差ey和旋轉誤差r x，如圖4（a）所示，測球與漸開線齒廓的接觸點將向上偏離于理論所在漸開線齒廓面的位置，此時可等效為齒輪漸開線存在線性誤差ezr，這兩者之間的轉換關系為：

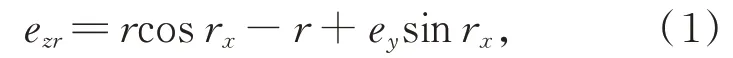
其中，r為齒輪漸開線樣板的基圓半徑。

若被測樣板存在線性誤差ey和旋轉誤差rz，如圖4（b）所示，測量點將產生Xw軸方向的偏移，偏移量exr為：

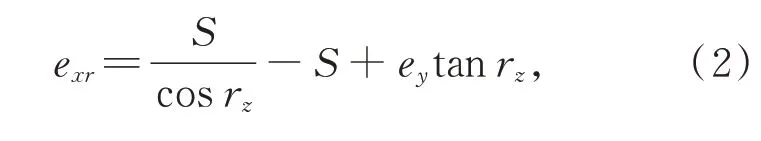
其中，S為基圓盤滾動距離，其值等于基圓半徑r與滾動角度φ的乘積，即S=rφ。

若被測樣板存在旋轉誤差ry和線性誤差ex、ez，如圖4（c）所示，通過幾何方法計算測量點的偏移量過程復雜，且一般求得的是近似解，精度稍顯不足。因此這里采用坐標系變換的方法：先求得實際測量點P'在工件坐標系ObXbYbZb中的坐標（xb，yb，zb），再通過坐標系變換求得該點在儀器坐標系OwXwYwZw中的坐標（xw，yw，zw），最后與理論測量點P在儀器坐標系中的坐標進行對比，從而得到測量誤差。由式（1）、（2）計算得到的ezr和exr都可以算入此種情況中的ez和ex。

圖4（c）中，r為理論基圓半徑，f1（ζ）為漸開線齒廓，f2（t）為測頭裝置中測桿所在直線，P'為實際測量點，P為理論測量點，ζ為實際測量點處的漸開線展開角，φ為理論測量點處的漸開線展開角。在XbObZb平面中，漸開線f1（ζ）的參數方程為：

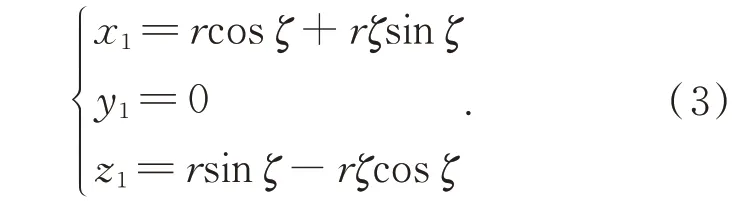
直線f2（t）在XbObZb平面中的參數方程為：

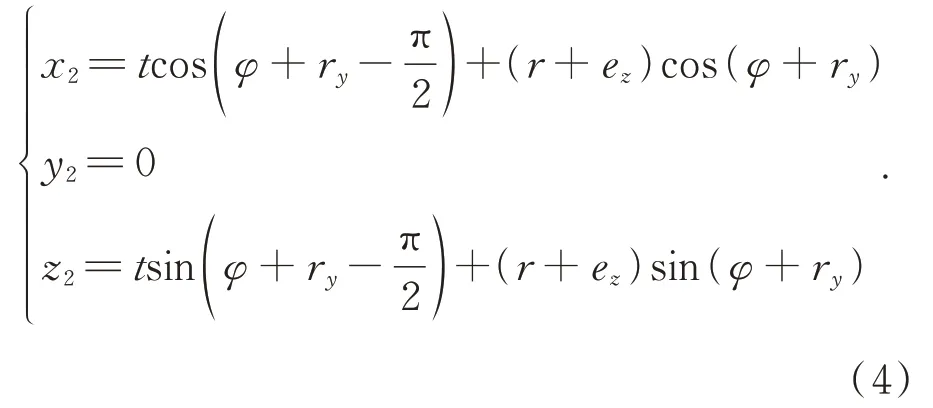
漸開線f1（ζ）與直線f2（t）在XbObZb平面內的交點聯合式（3）（4）可求得：

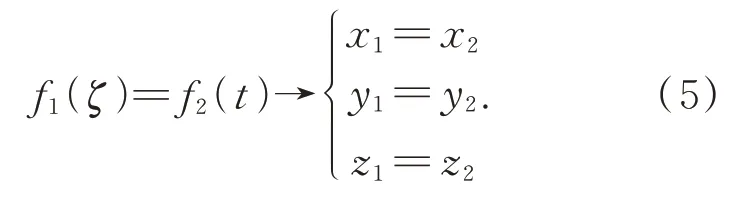
式（5）的解析解計算過程繁雜，但是數值解利用MATLAB軟件編程求解相對簡單得多，計算得到參數t、ζ，選其中一個代入相應的參數方程中，即可求得點P'在工件坐標系ObXbYbZb中的坐標（xb，yb，zb）。然后根據兩個坐標系的位姿關系，將ObXbYbZb坐標系繞Yw軸旋轉η=（φ+ryπ/2）角度，再沿Xw軸平移（ex+rφ）個單位，最后沿Zw軸平移（r+ez）個單位，求出實際測量點P'在儀器坐標系OwXwYwZw中的坐標（xw，yw，zw）：

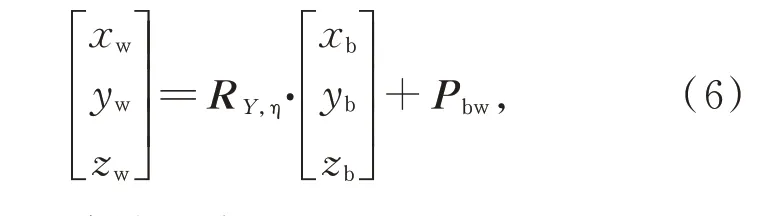
其中：R Y，η為旋轉矩陣，Pbw為平移向量，可由下式計算：

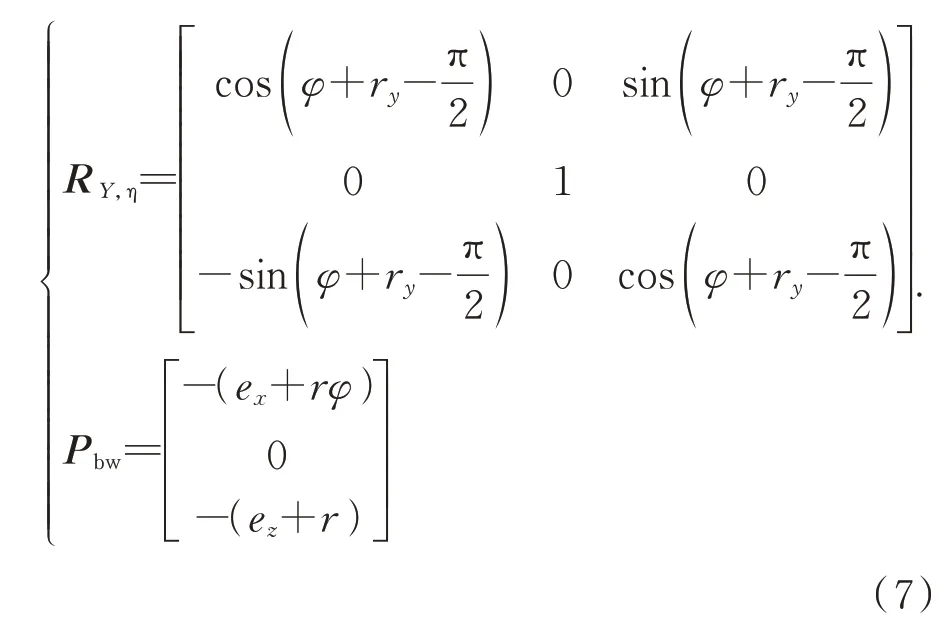
由于理論測量點P位于儀器坐標系的原點，故式（6）中實際測量點P'的橫坐標xw即為測量誤差Δ。

在展開長度ρs范圍內取多個測量點，所有點帶入式（8）獲得一條測量誤差曲線，從測量誤差曲線中能分離出齒廓總偏差Fα、齒廓傾斜偏差fHα和齒廓形狀偏差ffα。如圖5所示為測量誤差曲線的齒廓偏差示意圖。

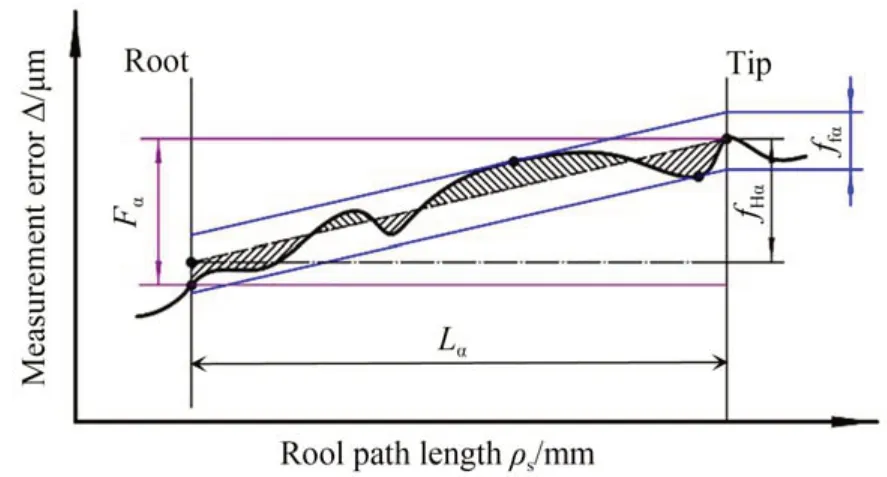
圖5 測量誤差曲線的齒廓偏差示意圖Fig.5 Diagram of the profile deviation of the measuring error curve

3 主要的空間幾何誤差源分析

上節分析的齒廓偏差補償模型能將6個空間幾何誤差對測量結果的影響計算出來。只要知道6個空間幾何誤差量，帶入模型便能計算出其帶來的齒廓偏差。本節針對雙滾輪-導軌式漸開線測量儀的主要兩項空間幾何誤差源展開具體分析。

3.1 基圓盤的圓度誤差

采用展成法測量漸開線的精確度在一定程度上依賴于基圓盤的各項精度指標?；鶊A盤的圓度誤差以橢圓形狀居多，本文針對此種情況帶來的測量誤差進行分析。基圓盤的圓度誤差會導致實際展開長度與理論展開長度不相等，從而產生線性誤差ex1；此外，兩個基圓盤的滾動距離也可能不等，進而導致芯軸產生旋轉誤差r z1；由于圓度誤差，基圓盤圓心到外圓的距離（即基圓盤的極徑）不等于理論基圓半徑r，從而導致被測樣板中心與理論位置存在線性誤差ez1及旋轉誤差r x1。圖6為基圓盤的圓度誤差帶來的空間幾何誤差示意圖。

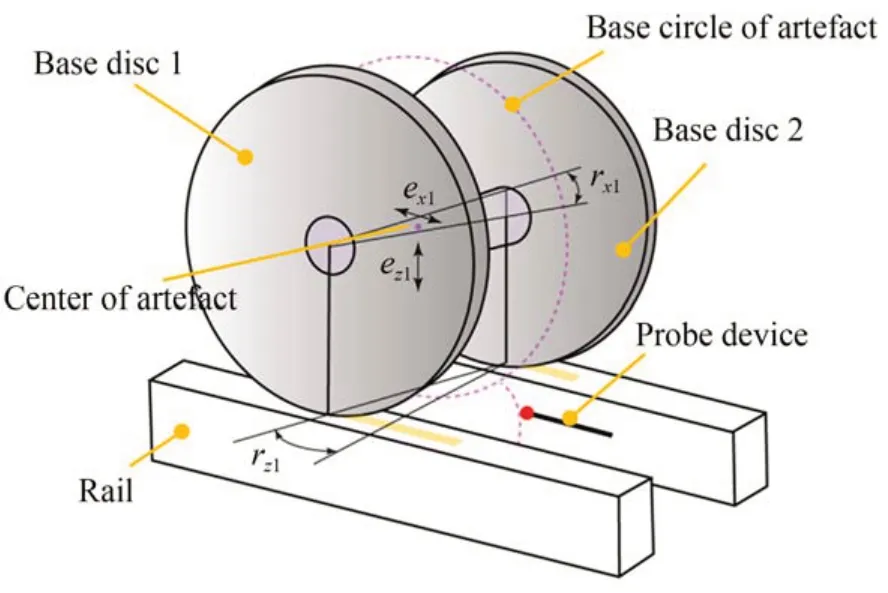
圖6 基圓盤的圓度誤差帶來的空間幾何誤差Fig.6 Spatial geometric errors caused by the roundness error of the base discs

設基圓盤1的長短軸半徑分別為a1、b1，基圓盤2的長短軸半徑分別為a2、b2，則圓度誤差κ=a-b。當基圓盤轉過φ角，被測樣板中心偏離于其理論所在位置的距離為：

其中：ρ1、ρ2分別為φ角時基圓盤1、基圓盤2的極徑。ρ1、ρ2可由下式計算：

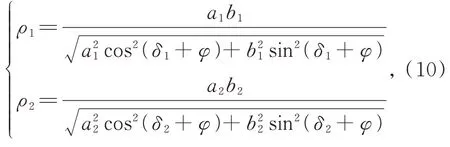
其中：δ1、δ2分別為基圓盤1、基圓盤2的初始極角，即基圓盤與導軌接觸點處的極徑和橢圓長軸之間的夾角。

齒輪漸開線樣板相對于儀器坐標系的旋轉誤差r x1為：

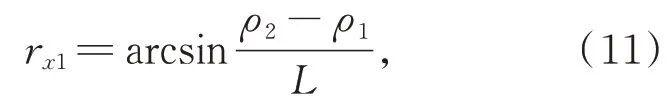
其中，L為芯軸的長度。

線性誤差ex1可由下式計算：

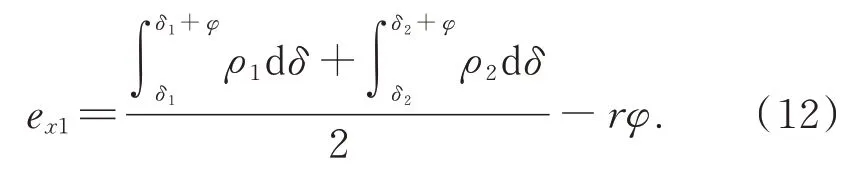
齒輪漸開線樣板相對于儀器坐標系的旋轉誤差rz1為：

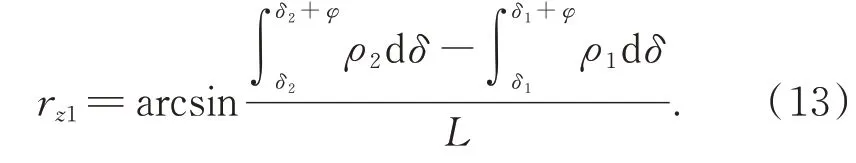
基圓半徑r為100 mm的齒輪漸開線樣板，展開角θ在0°～40°，展開長度ρs在0～70 mm。將基圓盤的圓度誤差引起的空間幾何誤差ex1、ez1、rx1、r z1帶入2.2節所述齒廓偏差補償模型，根據式（8）計算出測量誤差Δ1并分析得出以下結論：（1）當基圓盤的圓度誤差κ一定時，其引起的齒廓偏差隨著兩個基圓盤的初始極角δ1、δ2的變化而變化，且主要帶來的是齒廓傾斜偏差fHα；（2）當滾動區域對稱分布在兩個橢圓長軸（初始極角δ1=δ2=-θ/2=-20°）或 短 軸（δ1=δ2=（π-θ）/2=70°）時，帶來的齒廓總偏差Fα最大且相等，其中齒廓傾斜偏差fHα互為相反數。

圖7為基圓盤的圓度誤差引起的齒廓偏差與初始極角的關系曲線，δ1與δ2的取值范圍為［-90°，90°］，展開長度ρs在0～70 mm，為方便與實驗結果對比分析，兩個基圓盤的圓度誤差分別取值為0.4 mm和0.6 mm。

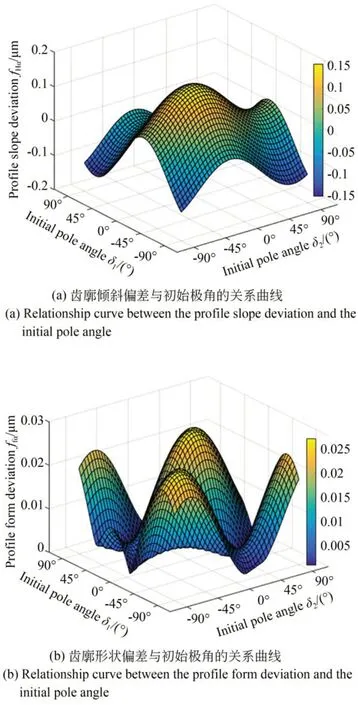
圖7 齒廓偏差與初始極角關系Fig.7 Relationship between the profile deviation and initial pole angle

3.2 純滾動組件的綜合安裝誤差

基圓盤的制造誤差除了外圓柱面的圓度誤差，還包括內孔的制造偏心等，此外，操作人員的技術水平也會帶來基圓盤和樣板的安裝偏心、偏擺問題。純滾動組件的綜合安裝誤差包括基圓盤和樣板相對于芯軸的綜合安裝偏心誤差和綜合安裝偏擺誤差?；鶊A盤若存在安裝偏擺，則滾動圓周為橢圓形狀，故基圓盤的安裝偏擺誤差對齒廓偏差的影響可等效于基圓盤的圓度誤差帶來的影響；齒輪漸開線樣板的安裝偏擺誤差等效于芯軸在兩個基圓盤內孔中安裝偏心方向相反的情況。因此這里對基圓盤和齒輪漸開線樣板的安裝偏擺誤差不做詳細分析，僅討論綜合安裝偏心的情況。

圖8為純滾動組件的綜合安裝偏心示意圖。圖中O1、O2、O3分別為基圓盤1、基圓盤2和樣板的圓心；e1、e2分別為芯軸在基圓盤1、基圓盤2的偏心量，e3為樣板在芯軸上的偏心量；λ1、λ2分別為芯軸相對于兩個基圓盤的偏心相位角（芯軸和基圓盤內孔圓心的連線與水平軸之間的夾角），λ3為樣板相對于芯軸的偏心相位角。λ1、λ2不相等會導致被測樣板產生偏擺，即存在旋轉誤差rx2和r z2。

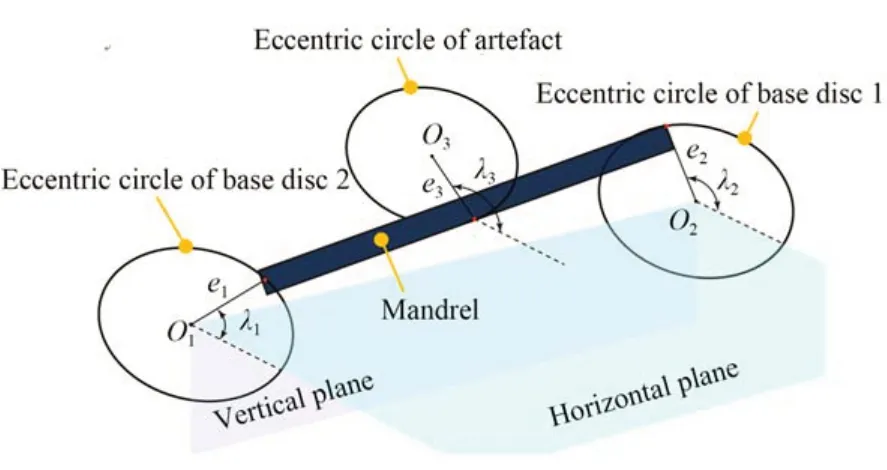
圖8 純滾動組件的綜合安裝偏心示意圖Fig.8 Comprehensive installation eccentricity diagram of a pure rolling component

綜合安裝偏心導致樣板相對于儀器坐標系產生4個空間幾何誤差：ex2、ez2、r x2和r z2，當基圓盤轉過角度φ時，水平方向產生的線性誤差ex2為：

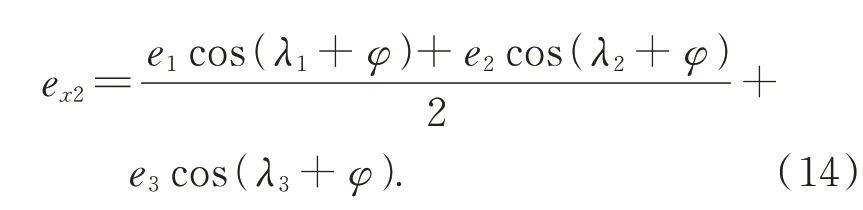
旋轉誤差rx2可由下式計算：

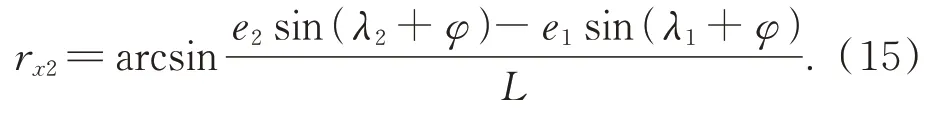
將上式帶入式（1）進而求得ez2：

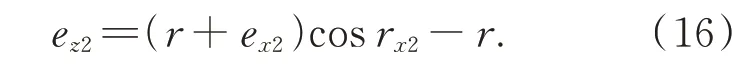
旋轉誤差rz2可通過下式求得：

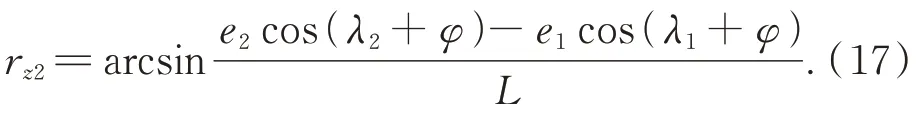
將ex2、ez2和r z2代入式（8）即可求得測量誤差Δ2。利用MATLAB對式（3）～（8）、（14）～（17）進行編程，畫出當三個偏心量e相等時，在展開長度ρs為0～70 mm范圍內齒廓偏差與三個偏心相位角的關系曲線，如圖9所示。為方便與實驗結果進行對比，偏心量的值取為3.46μm，分析得出以下三點結論（適用于三個偏心量相等的所有情況）：

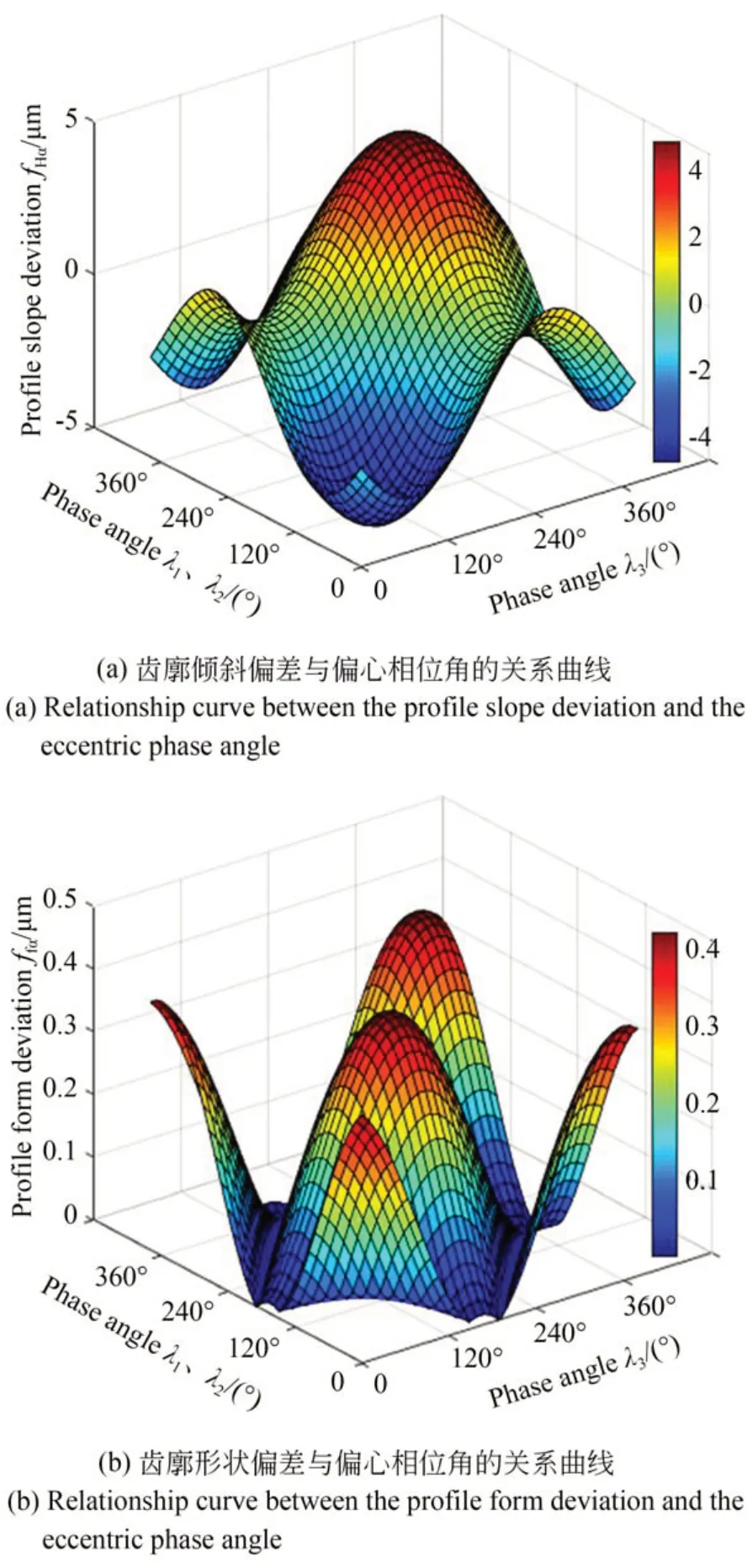
圖9 齒廓偏差與偏心相位角關系Fig.9 Relationship between the profile deviation and the eccemtric phase angle

（1）當偏心相位角λ1=λ2且與偏心相位角λ3相差180°時，綜合安裝偏心對測量結果沒有影響；

（2）當偏心相位角λ1=λ2=λ3=70°或250°時，綜合安裝偏心帶來的齒廓傾斜偏差fHα最大；

3）當偏心相位角λ1=λ2=λ3=160°或340°時，綜合安裝偏心帶來的齒廓形狀偏差ffα最大，不帶來齒廓傾斜偏差。

圖10為極限齒廓偏差f［max］與偏心量e的關系。由圖可知，極限齒廓偏差與偏心量成正比關系，其 中 極 限 齒 廓 傾 斜 偏 差fHα［max］為 偏 心 量 的136%；極 限 齒 廓 形 狀 偏 差ffα［max］為 偏 心 量 的12%。

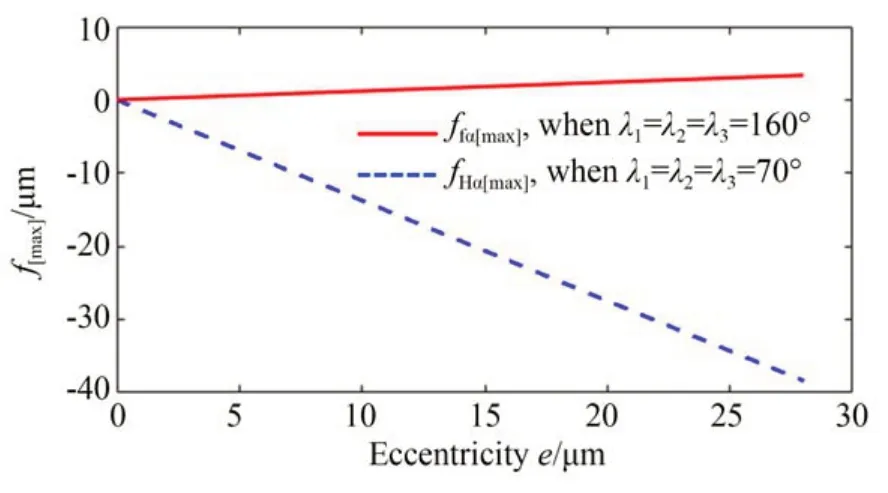
圖10 極限齒廓偏差f［max］與偏心量e的關系曲線Fig.10 Relationship curve between the extreme profile deviation f［max］and the eccentricity e

4 實驗驗證

為了驗證齒廓偏差補償模型的有效性，針對上節分析的兩項空間幾何誤差源設計相應實驗。實驗在室溫為20±0.5℃的大連理工大學高精度測量間進行，所有數據均重復5次測量，取平均值作為最終測量結果。

4.1 實驗準備

實驗前需要測量兩個基圓盤的圓度誤差大小和滾動組件裝配過程中的實際綜合安裝偏心大小?；鶊A盤的圓度誤差測量如圖11所示，選用分辨力為0.1μm的便攜式電感測微儀，電感測頭打在兩個基圓盤外圓和樣板兩側端面上（樣板的徑跳取兩側端面徑跳值的平均值），轉動芯軸至下一個測量點，直至芯軸轉動一周。由于此測量方法以頂尖為基準，因此需要將芯軸頂尖孔相對于各安裝軸段的偏心考慮進去，根據徑向跳動測量值擬合計算出基圓盤的圓度誤差，如圖12所示，基圓盤1的圓度誤差κ1=0.4μm，基圓盤2圓度誤差κ2=0.6μm。

圖11 兩個基圓盤的圓度誤差測量Fig.11 Roundness error measurement of the two base discs

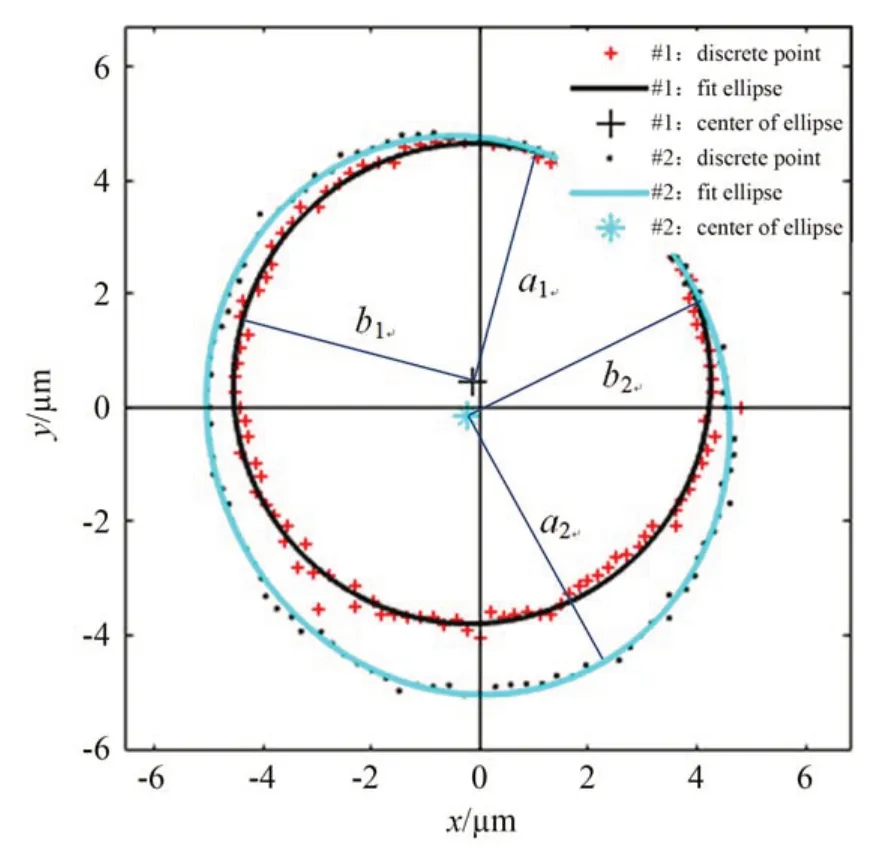
圖12 兩個基圓盤的圓度誤差Fig.12 Roundness error of the two base discs

純滾動組件的綜合偏心通過加裝G5級球制作的、具有微量過盈量的偏心密珠軸套實現［21］，圖13為特制偏心密珠軸套示意圖，移除密珠軸套均布六球室中Y方向的對稱兩球室里的球，在鎖緊螺母和平墊圈的作用下，被測工件偏心方向基本與Y方向一致，可通過更換不同直徑的密珠滿足不同偏心量的需求。

圖13 偏心密珠軸套Fig.13 Eccentric multi-ball bearing

用偏心密珠軸套依次裝配出如圖14中三種位姿的純滾動組件。裝配時控制不同位姿下的漸開線展開長度對應的基圓盤區域相同，芯軸與基圓盤的對應相位也相同，確保測量過程中只有綜合安裝偏心這一個變量影響測量結果。

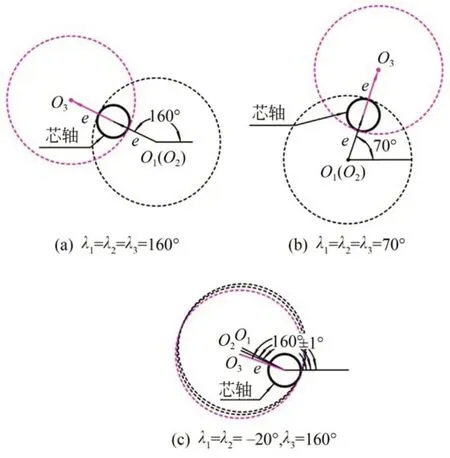
圖14 三種綜合偏心裝配位姿Fig.14 Three comprehensive installation eccentric positions

綜合偏心的測量方法和基圓盤的圓度誤差測量方法相似，補償掉芯軸頂尖孔相對于各安裝軸段的偏心后，計算出滾動組件的真實綜合安裝偏心值。偏心相位角λ1=λ2=λ3=70°情況下滾動組件的綜合安裝偏心值如圖15所示，從圖中可以看出偏心量為3.46μm，偏心相位的誤差為±2°。

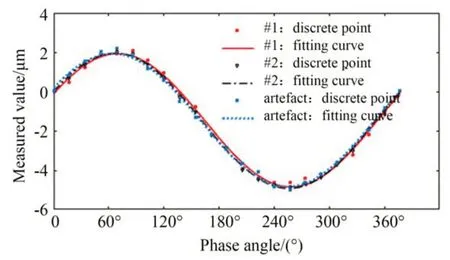
圖15 λ1=λ2=λ3=70°時純滾動組件的綜合安裝偏心Fig.15 Comprehensive installation eccentricity of the pure rolling element whenλ1=λ2=λ3=70°

4.2 實驗過程與結果

實驗所用齒輪漸開線樣板的基圓半徑r為100 mm，展開長度ρs在0～70 mm，評測計值區間Lα為5～70 mm。

為了驗證基圓盤的圓度誤差對測量結果的影響規律，將齒輪漸開線樣板的展開長度ρs對應的基圓盤圓弧段（即滾動區域）選取為三個不同區段，分別為對稱分布在橢圓長軸（初始極角δ1=δ2=-20°）、對稱分布在橢圓短軸（δ1=δ2=70°）和分布在長短軸之間（δ1=δ2=25°）。根據3.1小節的分析，δ1=δ2=-20°和δ1=δ2=70°帶來的齒廓傾斜偏差互為相反數，δ1=δ2=25°帶來的齒廓傾斜偏差為零，具有明顯的對比特征。

按上述初始極角值依次裝配好后將純滾動組件放置到實驗室自行研制的齒輪漸開線樣板激光干涉測量裝置上，測量齒輪漸開線樣板的齒廓偏差，如圖16所示。該測量裝置整合了雙滾輪-導軌式展成機構和任意表面形位誤差的激光測量測頭裝置，導軌的直線度誤差為20 nm/120 mm，激光干涉儀的測量精度約為15 nm，測量裝置補償部分誤差后對于漸開線齒廓偏差的測量不確定度可達0.4μm，精度符合實驗需求。

圖16 基圓盤的圓度誤差引起的齒廓偏差測量實景Fig.16 Real scene of tooth profile deviation measurement caused by roundness error of base disc

基圓盤的圓度誤差引起的測量誤差的實測曲線Δ1'如圖17所示，圖18為根據齒廓偏差補償模型畫出的滾動區域不同時的理論偏差曲線Δ1。

從圖17可以看出，在計值范圍Lα內，初始極角δ1=δ2=25°時的實測曲線相對于δ1=δ2=-20°時的實測曲線，齒廓傾斜偏差fHα減小了0.11 μm，齒廓形狀偏差ffα增大了0.04μm；δ1=δ2=70°時的實測曲線相對于δ1=δ2=-20°時的實測曲線，齒廓傾斜偏差fHα減小了0.31μm，齒廓形狀偏差ffα基本不變；與圖18中三條理論曲線的齒廓偏差變化規律基本一致。

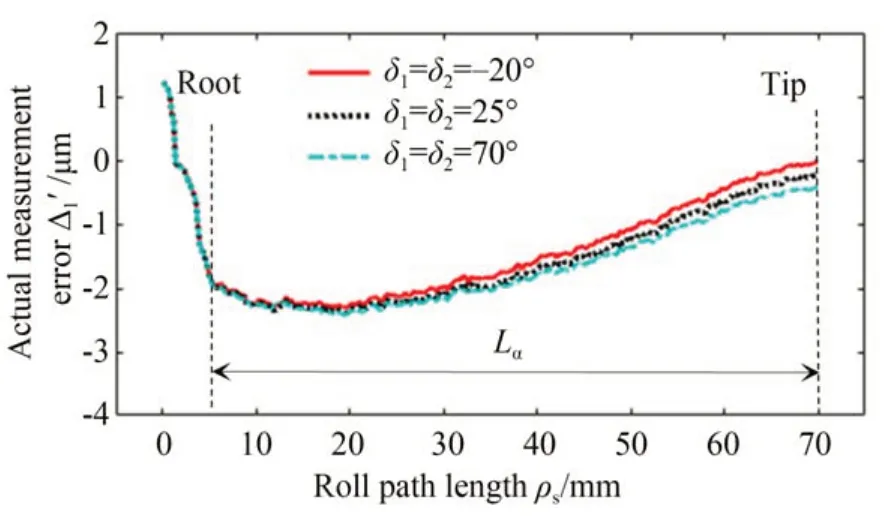
圖17 滾動區域不同時的實際測量曲線Fig.17 Actual measurement curve for different rolling areas

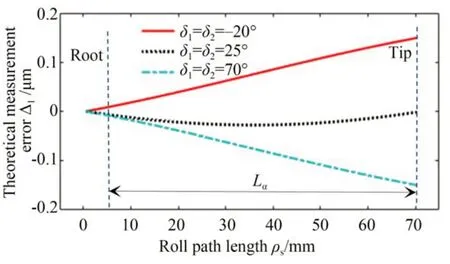
圖18 滾動區域不同時的理論偏差曲線Fig.18 Theoretical deviation curve for different rolling areas

表1為滾動區域不同時的測量結果，表中齒廓偏差理論值可通過圖7查找。從表1可以看出，將δ1=δ2=25°和δ1=δ2=70°的測量曲線減去δ1=δ2=-20°的測量曲線后（即#i-#1），在計值范圍Lα內實際齒廓偏差與理論齒廓偏差的差值不大于0.04μm。

表1 滾動區域不同時的測量結果Tab.1 Measurement results of different rolling area

為了驗證齒廓偏差補償模型的正確性，還針對基于齒廓偏差補償模型分析的綜合安裝誤差設計實驗驗證。依次測量偏心量為3.46μm的三種綜合偏心裝配位姿下被測樣板的齒廓偏差，所測得的實際誤差曲線Δ2'如圖19所示，理論偏差曲線Δ2如圖20所示。

從圖19可以看出，偏心相位角λ1=λ2=λ3=160°的實測曲線相對于λ1=λ2=-20°、λ3=160°的實測曲線，齒廓形狀偏差ffα增大了0.43μm，約為偏心量的12%，齒廓傾斜偏差fHα不變；λ1=λ2=λ3=70°的實測曲線相對于λ1=λ2=-20°、λ3=160°的實測曲線，齒廓傾斜偏差fHα減小了4.62μm，約為偏心量的134%，齒廓形狀偏差ffα基本不變；與圖20中三條曲線的齒廓偏差變化規律基本吻合。

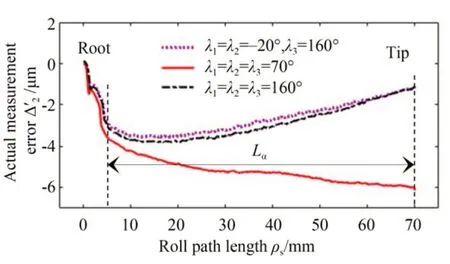
圖19 不同綜合安裝偏心下的實際測量曲線Fig.19 Actual measurement curve of different comprehensive installation eccentricity

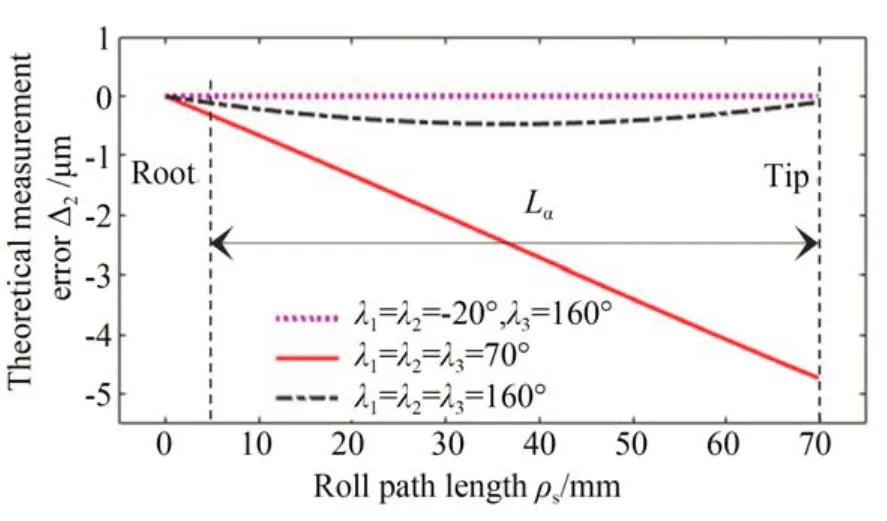
圖20 不同綜合安裝偏心下的理論偏差曲線Fig.20 Theoretical deviation curve of different comprehensive installation eccentricity

表2為不同裝配位姿下的測量結果，表中齒廓偏差理論值可通過圖9查找。從表2中可知，（#2-#1）的實際齒廓傾斜偏差與理論值的差值為-0.16μm，相對誤差約為4%；（#3-#1）的實際齒廓形狀偏差與理論值的差值為0.01μm，相對誤差約為2%。

表2 不同綜合安裝偏心下的測量結果T ab.2 Measurement results in different comprehensive installation eccentricity

考慮到測量裝置的系統誤差、測量重復性誤差和偏心相位誤差，測量結果與理論結果存在偏差在所難免。

實驗結果表明齒廓偏差補償模型能夠有效表征空間幾何誤差與漸開線齒廓偏差之間的計算關系，可通過安裝誤差之間的相互抵消或直接補償提高雙滾輪-導軌式漸開線測量儀的測量精度。

除此之外，在實驗過程中我們發現將兩個基圓盤和被測樣板調整成無偏心十分困難。相比之下，相位則容易得到控制，因此可以采用圖14（c）方式補償修正滾動組件綜合安裝偏心帶來測量誤差。

5 結 論

本文針對雙滾輪-導軌式漸開線測量儀器中存在的空間幾何誤差提出了一種補償新方法，該方法避免了超越方程求解一般公式的復雜性，只需確定幾何誤差量便能通過齒廓偏差補償模型直接計算出其帶來的齒廓傾斜偏差和齒廓形狀偏差；然后基于該補償模型對幾項常見的空間幾何誤差源（如漸開線樣板、基圓盤與芯軸的綜合安裝誤差，基圓盤的圓度誤差等）進行具體分析，得出初始誤差與齒廓偏差之間的映射關系，并對其進行實驗驗證，得到如下結論：

（1）將漸開線的展開長度區域選在基圓盤的不同使用圓弧段，實驗證明當滾動區域對稱分布在橢圓的長軸或短軸時，帶來的齒廓傾斜偏差最大，且方向相反，實測值與理論值的絕對誤差不大于0.04μm。

（2）齒輪漸開線樣板、基圓盤與芯軸的安裝偏心對齒廓偏差影響很大，其值的大小與偏心相位角相關。當偏心相位角λ1=λ2=λ3=70°時，帶來的齒廓傾斜偏差最大，與理論值的相對誤差約為4%；當偏心相位角λ1=λ2=λ3=160°時，帶來的齒廓形狀偏差最大，與理論值的相對誤差約為2%。

實驗結果證明了空間幾何誤差補償方法的有效性，該補償方法為實現基準級齒輪漸開線樣板的制造提供了測量手段。