一道不等式問題的解法探究
2022-03-31 08:55:06朱瓊
高中數理化 2022年5期
朱 瓊
(甘肅省酒泉衛星發射中心東風中學)
高中數學不等式知識是高等數學數學分析和實變函數等學科的基礎,是高中數學主干知識之一,也是高考重點考查的內容.因此,在平時的學習中,學生有必要對經典的不等式試題進行多解探究,以期提升數學學科核心素養.本文對一道不等式問題進行多解探究.

畫出g(x)的圖像,如圖1所示.
令g(x)=10,得x=-2或2.結合圖像可得不等式f(x)+|x-1|≤10的解集為{x|-2≤x≤2}.
以下著重對這道試題的第(2)問進行多解探究.
(2)方法1

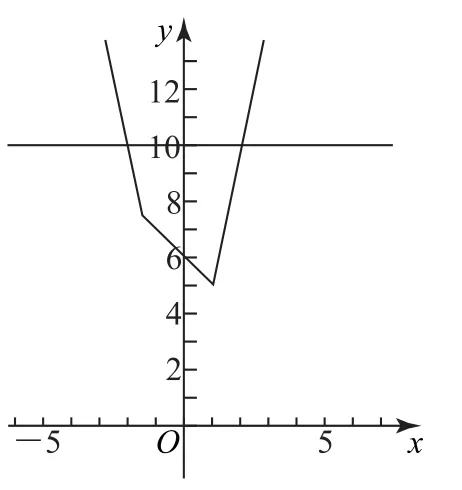
圖1


本解法運用了三角換元法,由待求式子聯想到三角函數的平方關系式,再分離出r.最后結合三角函數的最值和已知條件求出r的最小值,從而求出a2+b2的最小值.


本解法用b表示a后,代入a2+b2=t,整理后將其看成以b為主元的二次方程,根據方程有實根,則判別式大于或等于0,得出t的最小值,從而得出a2+b2的最小值.


由已知條件聯想到直線方程,由a2+b2聯想到直線上的點與坐標原點的距離的平方,再由點到直線的距離公式可以求出d的最小值,從而求出a2+b2的最小值.


本題先用b表示a,再代入a2+b2,最后利用二次函數的最值求出函數f(b)的最小值.
本文利用高中數學中學習過的柯西不等式、三角函數、向量、一元二次不等式以及距離公式等對例題進行多解探究,體現了數學知識的綜合性,創新了試題的解法.多解探究可以引發學生學習興趣,培養數學運算和邏輯推理的數學素養.下面給出3道練習題供讀者參考.


猜你喜歡
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
中等數學(2021年11期)2021-02-12 05:11:46
新世紀智能(高一語文)(2020年10期)2021-01-04 00:44:12
新世紀智能(高一語文)(2020年10期)2021-01-04 00:44:10
新世紀智能(高一語文)(2020年12期)2020-06-01 08:14:28
新世紀智能(高一語文)(2020年12期)2020-06-01 08:14:26
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52

