金紅石型二氧化鈦薄膜熱導率的數值模擬

白素媛， 白容榕， 吳 可

(遼寧師范大學 物理與電子技術學院，遼寧 大連 116029)

作為禁帶寬度達到3.2 eV的無機半導體多功能材料，二氧化鈦有著無毒、成本低、抗腐蝕、高光催化活性等特點，且熱、物理、化學性質穩定，被廣泛應用于染料敏化太陽能電池、介敏材料、光學催化劑、氣體傳感器、電致變色器件等研究方面.作為自然界中二氧化鈦存在的形式之一，金紅石擁有良好的光散射和光反射性能，折射率高，無毒，無論是強酸還是強堿環境中都具有化學惰性，因此是最穩定的熱力學材料.盡管金紅石與銳鈦礦相相比具有較低的電子遷移率，但這些特性使其在光電應用方面也具有吸引力，如太陽能電池[1].

作為染料敏化太陽能電池的重要組成器件之一，二氧化鈦的散熱效果對太陽能電池的光電轉化效率有著顯著影響，因此二氧化鈦作為熱電材料受到了人們的廣泛關注.Maekawa等人通過金屬有機化學氣相沉淀法合成了不同形貌的二氧化鈦薄膜，并研究其微觀結構對薄膜熱導率產生的影響[2].Kim等人使用3ω法測定了直流磁控濺射法制備的4種二氧化鈦薄膜在80 K到室溫溫度范圍內的導熱系數[3].Donovan等人通過分析模型進一步了解了二氧化鈦熱傳輸的趨勢，并確定了本征點缺陷對金紅石型二氧化鈦熱傳輸的影響[4].熱導率的測量具有重要意義，因為它包含有關材料微觀結構的信息，有助于分析各種器件的性能.隨著理論與計算模擬的發展，分子動力學(MD)方法已經逐漸成為模擬預測一些難以通過實驗方法測量的材料的重要手段，特別是在納米尺度上，MD方法為預測導熱性、揭示影響薄膜導熱機制和因素等方面提供了一種很有前景的選擇.Fujiwara等人基于平衡分子動力學和非平衡分子動力學計算研究了納米流體的熱導率,并闡述了熱導率變化的機制[5].本研究小組利用分子動力學方法，基于COMPASS力場，測量了低維納米材料室溫下的導熱率[6].Momenzadeh等人采用平衡分子動力學方法，確定了金紅石型二氧化鈦的晶格導熱系數[7].盡管如此，與眾多實驗方法研究相比，利用MD方法對二氧化鈦熱導率進行數值模擬的研究工作較少，因此本文借助MD方法，通過二氧化鈦薄膜的厚度和氧空位濃度這些因素的改變，計算分析其對薄膜熱導率的變化關系.

1 理論基礎

1.1 非平衡分子動力學方法(NEMD)

分子動力學計算模擬薄膜熱導率主要有EMD和NEMD[8]兩種方法.EMD即模擬體系在平衡狀態下的熱導率，其基于Green-Kubo方程.NEMD即對系統施加擾動，建立非平衡熱傳輸過程，模擬非平衡導熱，基于Fourier定律[9]計算求得熱導率.因為現實中系統常常設有溫度梯度，且具有不可逆熱流，而通過NEMD可以對這種不可逆非平衡過程進行模擬.基于以上考慮，本文選擇通過NEMD進行二氧化鈦薄膜熱導率的計算模擬.

1.2 系綜

分子動力學模擬計算給出模擬體系的微觀信息，通過統計物理學將微觀狀態下的相關參數轉化為宏觀性質，因此引入系綜這一概念.常用的系綜除了有微正則系綜(NVE)、正則系綜(NVT)、等壓等焓系綜(NPH)，還有等溫等壓系綜(NPT).其中，在NVE系綜里，粒子沿著相空間中的恒定能量軌道演化，體系中的粒子數N和體積V恒定，與外界不產生任何能量交換，不需要重新控制體系的能量，因此本文在對金紅石型二氧化鈦薄膜的研究中選用微正則系綜.

1.3 COMPASS勢函數

分子動力學模擬中，建立正確的勢函數模型是必要前提，其用來描述粒子間的相互作用，直接關系到模擬的準確性和正確性，因此選擇合適的勢函數至關重要.其中Buckingham勢函數、Morse勢函數、Lennard-Jones勢函數等兩體勢應用較為廣泛，常見的多體勢有Stillinger-Wab勢函數、Tersoff勢函數、MEAM勢等，此外還有力場.常見的力場有DERIDING力場、UNIVERSAL力場、COMPASS力場.本文采用了COMPASS力場[10]對金紅石型二氧化鈦薄膜進行模擬計算，作為凝聚態優化分子勢，其勢函數形式可表達為

E=Eb+Eθ+Eφ+Eχ+Ecross+Eij+Eelec=

(1)

其中，k、H、V、A、B為力常數，b為鍵長，θ為鍵角，φ為二面角，ε為能量參數，rij為原子與原子間距，q為電荷量.由鍵合項和非鍵合項構成了力場能量.其中鍵伸縮能、鍵角彎曲能、鍵鈕轉能、鍵角面外彎曲能及相互耦合能為鍵合項.范德華力、庫倫力以及原子對之間的相互作用力為非鍵合項.

2 模擬過程與結果

在系統中建立金紅石型二氧化鈦基本單元，其結構如圖1所示，根據周期性邊界條件，選取的截斷半徑不宜過小，其原因是為了防止系統中粒子間相互作用，且模擬系統中粒子過多會對計算機運行速度產生一定的影響.基于以上考慮，本文在建立超晶胞時分別在X、Y方向上選取4個基本單元，在厚度Z方向上選取24個基本單元，如圖2所示為金紅石二型氧化鈦超晶胞計算模型.

圖1 金紅石型二氧化鈦基本單元結構模型

圖2 金紅石型二氧化鈦4×4×24計算模型

2.1 膜厚對二氧化鈦薄膜熱導率的影響

在進行非平衡分子動力學模擬時，需要判斷模擬體系是否達到穩態，本文采用觀察系統中Z方向上的溫度分布曲線是否光滑來進行判斷.以計算模型4×4×48(即厚度7.10 nm)為例進行初步模擬，體系溫度為300 K，時間步選取為1.0 fs，如圖3所示分別為模擬步數50萬步和250萬步時的溫度分布曲線.經兩圖比較可知，隨著計算步數增多，溫度分布曲線逐漸光滑，可以判斷系統在250萬步計算后達到了平衡狀態.

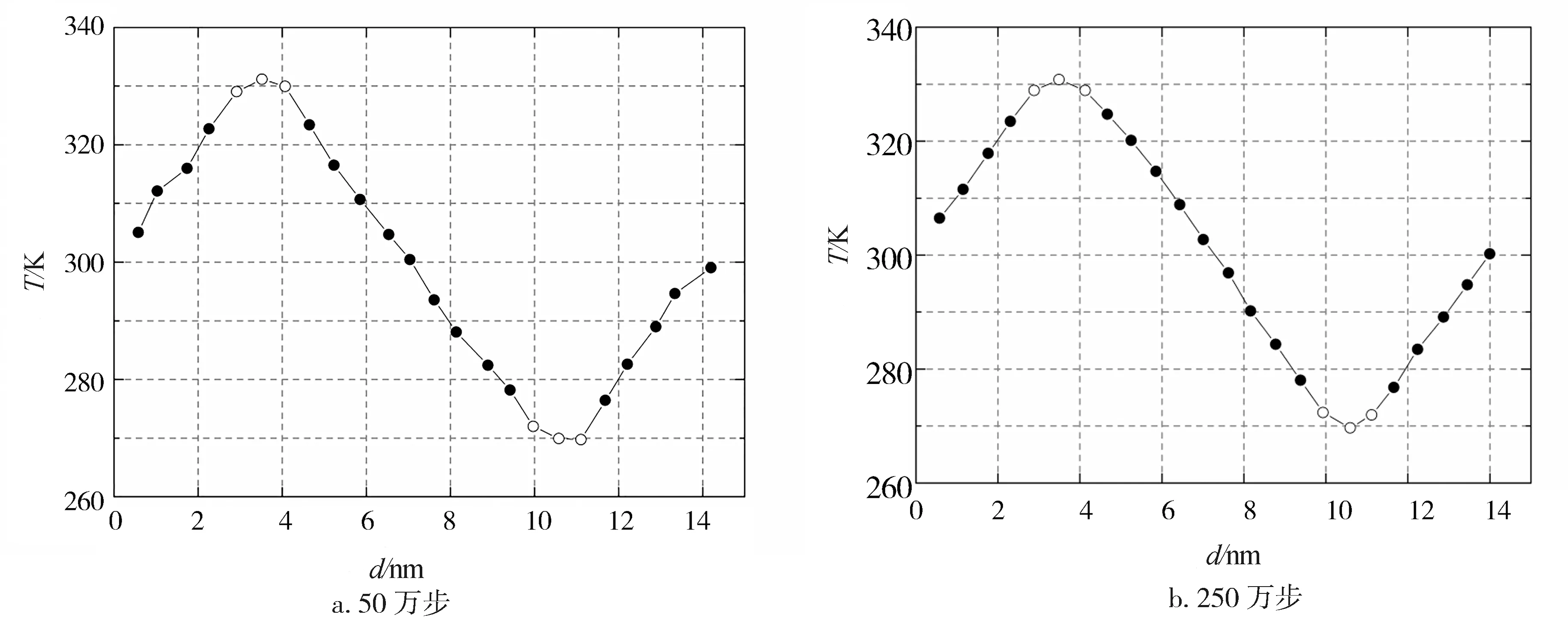
圖3 不同計算步數下各層溫度分布曲線

表1為室溫300 K下不同膜厚的二氧化鈦薄膜的熱導率，由表1能夠觀察到薄膜厚度范圍在5.92～8.29 nm內變化的二氧化鈦薄膜，其熱導率在1.899～2.522 Wm-1K-1之間.圖4為二氧化鈦薄膜不同厚度下的熱導率變化曲線圖，由此圖可看出，其熱導率隨著薄膜厚度的增大而增大，兩者接近于線性變化，圖像呈示出顯著的尺寸效應.

表1 不同厚度的二氧化鈦薄膜熱導率的計算結果

圖4 熱導率與薄膜厚度的變化曲線

根據德拜理論可得出晶格熱導率為

(2)

其中,c為單位體積比熱容，v為聲子平均速度，leff為有效聲子平均自由程.由式(2)可以看出，當膜厚d遠超過聲子平均自由程l時，聲子與邊界進行碰撞的概率很小，聲子的平均自由程在碰撞過程中可保持恒定不變，熱導率也因此保持一定值；當d與l相等或d小于l時，聲子與邊界進行碰撞的概率變大，此時需要考慮到散射作用對熱量傳輸的影響，因此聲子的平均自由程在碰撞過程中變小，熱導率也隨之變小；當膜厚d遠小于聲子平均自由程l時，熱導率隨膜厚變小而變小這一特點越來越明顯.影響聲子平均自由程的因素主要是聲子的散射，如聲子與聲子之間的散射，邊界對聲子的散射等.這些散射機制對材料的傳熱性能有顯著影響，因此，當膜厚d由5.92 nm增長到8.29 nm并遠小于聲子平均自由程l時，聲子邊界散射作用減小，熱導率隨之增加，且熱導率與薄膜厚度接近于線性變化，表現出鮮明的尺寸效應.

將本文模擬結果與該文獻[7]進行對照，雖然所用計算模擬方法和膜厚范圍不同，導致測得的熱導率結果有所差別，但得到的變化趨勢一致，由此可以看出本文模擬結果具有合理性.

2.2 濃度對空位缺陷型二氧化鈦薄膜熱導率的影響

現實中晶體總是存在一定數量的缺陷或瑕疵，而這種缺陷對材料的性質必然會造成一定的影響.通常人們認為二氧化鈦中的缺陷對材料的性能具有負面影響，但研究表明，適當的缺陷在一些條件下可以使材料的性能得到改善，甚至會產生某些新功能.Yoon等人觀察到含氧缺陷的銳鈦礦型二氧化鈦薄膜具有居里溫度高達800 K的高溫磁鐵性[11].Sung等人研究了二氧化鈦中氧空位梯度對雙極型電阻式存儲器切換方向的影響[12].Wang等人研究了含氧缺陷的二氧化鈦可作為鋰硫電池的新型功能主體[13].氧空位的存在使二氧化鈦的電導性、鐵磁性和光響應等性質發生明顯變化，二氧化鈦的熱導率也可能受到氧空位的影響，其相關研究和文獻卻并不多，所以本文就氧空位濃度與金紅石型二氧化鈦薄膜熱導率之間的變化關系進行相關模擬計算.

采用非平衡分子動力學模擬方法，將空位濃度定義為產生空位的原子數與模擬體系總原子數的比值.仍采用計算模型4×4×48(即厚度7.10 nm)來進行模擬，此時模擬體系中的總原子數為4 608個.在5組基本模型中分別隨機抽取3、4、5、6、7個氧原子，空位濃度分別為0.065%、0.087%、0.109%、0.130%、0.152%，圖5為空位缺陷結構示意圖.經過模擬計算，在系統溫度300 K下，氧空位濃度為0.109%的二氧化鈦薄膜各層的溫度分布曲線如圖6所示.

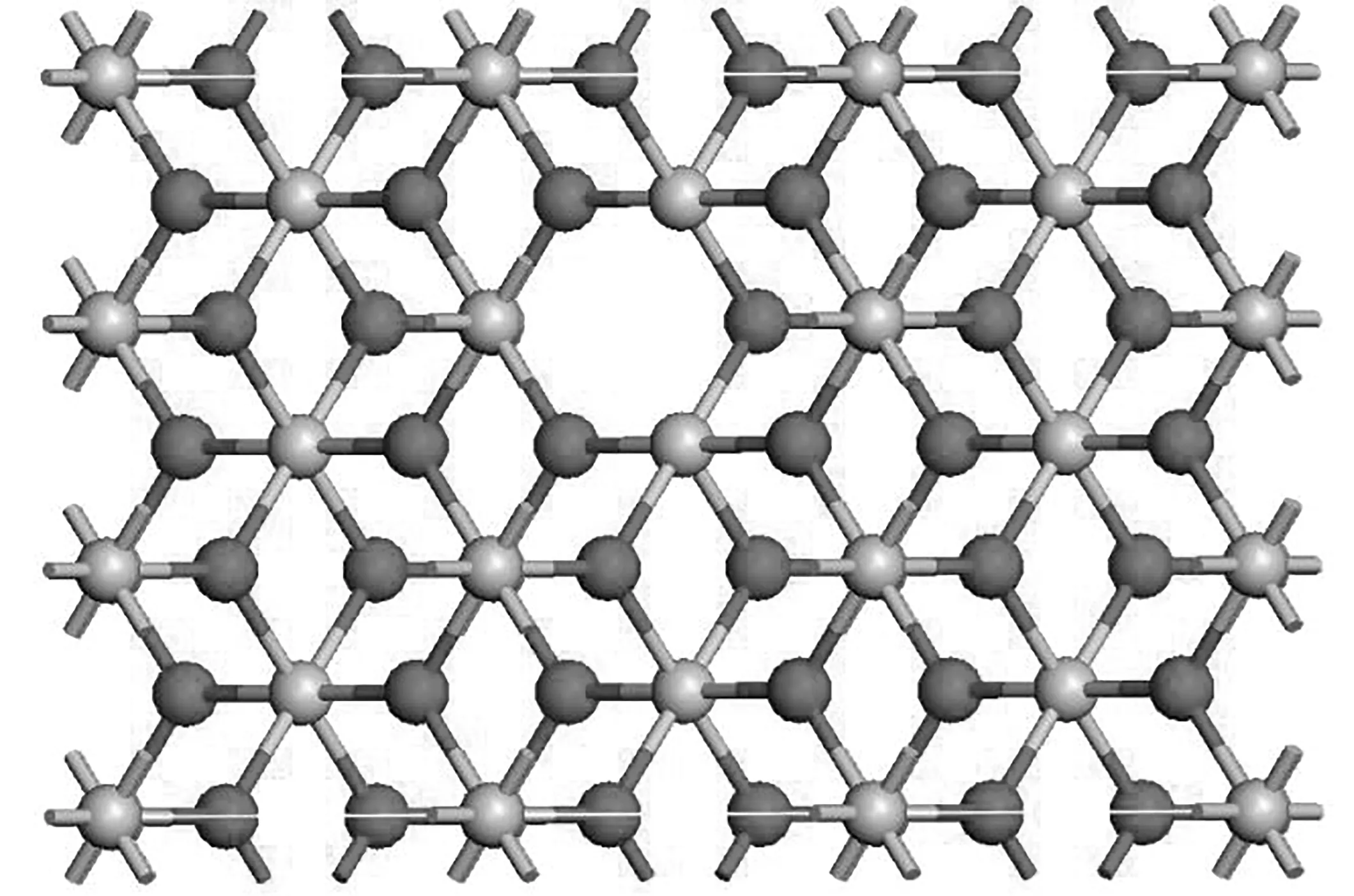
圖5 空位缺陷結構示意圖

圖6 空位濃度為0.109%的二氧化鈦薄膜溫度分布曲線

表2為二氧化鈦薄膜在系統溫度300 K下不同氧空位濃度時的導熱系數，由表2可知氧空位濃度在0.065%～0.152%范圍內變化的二氧化鈦薄膜，其熱導率在2.148～1.705 Wm-1K-1之間.圖7為含氧空位缺陷的二氧化鈦薄膜與氧空位濃度之間的變化曲線.可以看出，氧空位的存在使二氧化鈦薄膜熱導率下降，且熱導率會隨著氧空位濃度的增加而減小.晶體內熱傳遞主要靠聲子的散射來完成，由于晶體內有空位的存在，體系中出現聲子與缺陷的散射，使得熱導率隨著聲子平均自由程的減小而減小.文獻[14]采用Tersoff勢函數模擬了不同空位濃度下硅薄膜熱導率的變化，得到空位缺陷使熱導率降低與聲子的散射有關，與本文研究結果相類似.

表2 不同空位濃度的二氧化鈦薄膜熱導率的計算結果

圖7 熱導率與空位濃度的變化曲線

3 結 論

本文在COMPASS力場下，基于NEMD方法，選用NVE系綜對系統溫度300 K下的金紅石型二氧化鈦薄膜熱導率進行計算模擬.模擬結果表明：二氧化鈦薄膜熱導率隨著薄膜厚度的增大而增大；當二氧化鈦薄膜厚度不變時，熱導率會隨著氧空位濃度的增大而減小.應用德拜理論進行理論分析，同時對模擬計算結果與其他文獻實驗結果進行分析與比較，證實了本文模擬結果的可靠性和合理性，具有重要參考作用.