基于POI數據的天津市體育設施空間格局分析

侯英姿， 高一冉， 王方雄， 畢紅星

(1.遼寧師范大學 地理科學學院，遼寧 大連 116029； 2.遼寧省自然地理與空間信息科學重點實驗室，遼寧 大連 116029；3.東北財經大學 體育經濟研究中心，遼寧 大連 116025)

隨著健康中國發展理念的提出，國家更重視體育事業的發展.在落實規劃設定的任務中，體育設施布局的合理性顯得尤為重要.然而傳統的調查手段不具有時效性，隨著網絡的發展，城市設施興趣點數據越來越引起人們的關注.在當前數字城市規劃中，體育設施興趣點在地理空間中與道路，人類活動有密切的聯系.采用合理的方法分析體育設施的空間分布，對城市體育設施的管理，布局，決策有一定的意義.不同POI類別的相關性和自身影響力不同，池嬌，康雨豪，趙衛峰，朱建成等人在利用POI數據對城市進行研究時都提出了對不同屬性類別的POI數據賦予不同權重值的研究方法[1-4].在點的特征表達方面，核密度分析方法滿足了地理學第一定律的要求，即距離衰減效應，因此經常被許多國內的學者用于點數據的空間聚集形態的研究[5-12].但這種傳統空間點模式分析方法沒有考慮到實體空間是非均質的，各向異性的，Okaba研發工具(SANET)將平面核密度升級為基于空間網狀結構的網絡核密度[13-15]，禹文豪等人基于Okaba的Dijkstra路徑算法提出一種一維形態算子的算法來優化計算時間,并在考慮道路網絡的通達方向、通行能力、以及發生元權重的條件下進行擴展研究[16-17].楊靜、曾璇、王爽等人在對POI數據進行空間熱點的分析中都采用了網絡核密度分析方法[18-20].網絡核密度分析通常表現在道路網絡上，空間區域不夠直觀，黃怡敏等人采用普通克里金空間插值的方法將結果與空間范圍進行關聯來劃分不同的功能區類別.K函數方法能在多個尺度上表現要素的空間相關性(聚集或離散)，但平面K函數可能會高估道路口旁的要素聚集或離散程度，對此，Okaba等人將平面空間K函數法升級為基于空間網狀結構的網絡K函數法[21].楊玨婕等人采用網絡K函數的分析方法對西雙版納人工林空間格分布的影響因素進行探究[22].鄔倫等人采用單變量和雙變量網絡K函數分析方法對餐飲設施點的空間分布影響因素進行研究[23].

目前采用網絡核密度的分析方法并沒有考慮到單個POI設施點影響力的不同，因此本文以天津市中心城區為例，對體育設施點采用網絡核密度分析.網絡核密度的結果只表現在道路，所以對其進行克里格差值，并與帶有權重的平面核密度柵格圖層疊加，最終分析體育設施點在權重和道路網絡約束下的空間分布聚集特征.并采用雙變量網絡K函數方法對體育設施熱點區域的不同影響因素進行研究.

1 數據來源和研究方法

1.1 研究區與數據來源

天津是我國的四大直轄市之一，地處于華北平原北部，市區包括中心城區，環城區，濱海新區和遠郊區.其中心城區是天津的發祥地，因此本文選取天津市的中心城區作為研究區域，包括紅橋區、河北區、南開區、和平區、河西區和河東區6個區域.根據數據的典型性原則，本文選取了保齡球館，壁球場，高爾夫，戶外健身場所，滑雪場，健身中心，籃球場館，溜冰場，馬術俱樂部，乒乓球館，賽馬場，水上活動中心，臺球廳，跆拳道場館，網球場，游樂場，游泳館，運動場所，綜合體育館，足球場等16個類別的體育設施點數據共1 280個，還包括居民小區162個，公交站點209個和餐飲設施517個點數據，均來自于高德地圖(2018年).POI數據包括名稱，地址，經緯度，設施類型等信息.

本文還應用了天津市2018年路網矢量數據，由于要在精細尺度下研究城市路網，所以獲取了大部分道路數據，包括地鐵，都市高速路，高速公路，國道，省道，九級路，鐵路，縣道，鄉鎮道路，人行道路，其他道路 .并利用天津中心區和街道數據識別研究區域.

1.2 研究方法

1.2.1 權重賦分方法

不同類型的POI數據對城市的功能屬性影響不同，同理不同類別的體育設施點對城市的影響力不同，因此需要對體育設施點數據進行權重系數測定.本研究通過網上查詢，大致確定各種體育設施點的平均占地面積.根據不同屬性的體育設施點的服務范圍以及占地面積不同，進行綜合賦分評價，最終確定權重分值區間[1,100].對于服務范圍廣，占地面積較大的體育設施點，賦予較高的權重值.例如：天津奧體中心，服務于全市范圍，是綜合性市級體育中心，占地7.8萬m2，賦值權重為100.

1.2.2 網絡空間核密度分析

通常地理學中對于點模式分析的表達方法都會應用核密度分析，是根據該點與相鄰點間空間關系所決定的聚集強度關于空間密度的一種場表達.它遵循了地理學第一定律距離衰減效應，距離中心點越近的區域受到的輻射值越大[13].傳統的歐式距離忽略了實際的空間特性[19].在道路網絡的約束下，網絡核密度分析方法能更加準確的表達體育設施的空間分布特征.其計算公式為

(1)

式中：f(s)是地理空間位置s處的核密度計算函數；r是路徑距離衰減閾值，即帶寬；n是與位置s的路徑距離小于或等于r的設施點的個數；dis是i點到設施s點的最短路徑距離；k是空間權重函數.式中存在兩個重要的參數k和r.其中，k的選擇對空間點的格局分布沒有太大影響，r的選擇是需要注意的問題.即在網絡的通行能力的約束條件下，計算網絡核密度.

1.2.3 網絡雙變量K函數法

網絡K函數法與平面K函數法分析思路相似，只是量算距離方式不同，網絡K函數法的距離采用的是兩點之間最短路徑距離.雙變量K函數法主要用來研究在道路網絡約束下一類點對象的分布對另外一類點對象分布的影響.在網狀空間結構中，有A=(a1,a2,…,an)，B=(b1,b2,…,bn)是道路網絡上的2個事件集，LT表示網絡數據集，|LT|為網絡總長度.理論期望值,其雙變量K函數K(t)[21]：

(2)

式中：E為對任意點bi∈B的理論期望值；ρa為A事件集的密度，即ρa=na/|LT|.觀測值,其雙變量K函數值Ka(t)為

(3)

如果觀測值大于理論期望值，則說明事件點呈聚集分布模式；如果觀測值小于理論期望值，則說明事件點為離散分布模式[19].

2 天津市體育設施區位布局研究

2.1 體育設施的集聚中心分析

本研究選取2018年天津市中心區體育設施點數據進行網絡核密度分析.一般網絡核密度衰減閾值選取為較大值如1 000、2 000 m，研究趨勢較為宏觀，本文想從精細尺度下進行研究，因此本文選擇的帶寬為200 m，衰減閾值小，聚集的信息較為豐富.利用SANET中“kernel density estimation”工具實現.傳統核密度法會使各位置獲得較高的密度值，這會高估空間設施點的聚集程度，與之相比，網絡核密度法引入路徑距離計算方法，使得核密度被約束到道路網絡附近，空間各位置密度值顯著降低，能夠客觀反映實際的空間分布特征.

由于對擬合的精度要求較高，本文采用克里格空間差值方法.其中普通克里格方法應用比較廣泛，該方法的變異函數中球面模型應用于地學統計分析，因此空間差值的方法選用普通克里格球形模型.空間插值的搜索半徑與網絡核密度衰減距離閾值相同，并與帶有權重的平面核密度柵格圖層疊加.為了直觀表達信息，對疊加柵格核密度值進行200 m格網分區統計，列出密度值最高的前20個街道如(表1)

表1 天津市賦權網絡核密度值前20名街道匯總

結果表明，天津市中心區體育設施的空間分布從整體上看具有“西南密東北疏”的分布特征，并且呈現多中心點聚集.其中網絡核密度聚集較高的密度區有體育中心街道、柳林街道、學府街道、天塔街道.體育設施分布密度次之的包括桃園街道與大營門街道交界、小白樓街道、邵公莊街道與西沽街道交界處、向陽樓街道、南市街道等.體育中心街道位于南開區，是2008年奧林匹克舉辦地，有許多運動場館，例如：天津體育館、天津奧林匹克中心、奧體中心體育場、奧林匹克訓練場、籃球場、羽毛球館等多種類別.柳林街道位于河西區，天津科技大學所在地，有天津科技大學體育館，體育中心，足球場，網球場等，天津市河西體育場，另外體育設施圍繞的商業中心就是泉匯購物廣場，包括許多健身運動場館俱樂部.學府街道位于南開區，是南開大學、天津大學、四十三中學所在地.天塔街道位于河西區，是天津體育學院的所在地，有許多體育運動場館.桃園街道與大營門街道交界位于河西區，是天津外國語大學所在地，包括許多體育運動場館.小白樓街道位于和平區，有新華路體育場和和平體育館兩個綜合體育館，還有網球場、游泳館、羽毛球館.邵公莊街道與西沽街道交界處位于紅橋區，是歐亞達商業廣場的所在地，有許多游樂場、跆拳道場.向陽樓街道位于河東區，有許多籃球訓練場館.其中，體育中心街道、柳林街道、學府街道呈現多中心點核密度分布.由此可見，體育設施核密度較高的地區一般分布于學校和商業中心地區.大學對于體育設施分布的影響較大，商業中心分布各種健身瑜伽館、臺球、網球、游泳館等體育休閑娛樂項目.

3 體育設施熱點空間格局影響因素分析

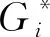
如圖1所示，在0～1 800 m范圍內，體育中心街道體育設施和居民小區的雙變量K函數觀測值曲線在理論期望值曲線之下，說明在此尺度范圍內，二者之間存在相互排斥的離散分布關系.在1 800～4 000 m范圍內，觀測值曲線在理論期望值曲線之上，位于蒙特卡羅模擬置信區間之內，說明兩者之間存在一定聚集關系.在0～800 m范圍內，柳林街道體育設施和居民小區的雙變量K函數觀測值曲線在理論期望值曲線之上，說明在此尺度范圍內，二者之間存在相互聚集分布關系.在800～2 100 m范圍內，觀測值曲線在理論期望值曲線之下，位于蒙特卡羅模擬置信區間之內，說明兩者之間存在離散關系.在2 100～3 500 m范圍內，二者之間存在相互聚集分布關系.在0～750 m范圍內，體育中心街道體育設施和公交站點的雙變量K函數觀測值曲線在理論期望值曲線之下，說明二者之間存在排斥的離散分布關系.在750～4 000 m范圍內，觀測值曲線在理論期望值曲線之上，位于蒙特卡羅模擬置信區間上限之外，說明兩者之間存在顯著性的空間聚集關系.在0～350 m范圍內，柳林街道體育設施點和公交站點的雙變量K函數觀測值曲線在理論期望值曲線之上，位于蒙特卡羅模擬置信區間之內，說明兩者之間存在一定聚集關系.在350～420 m范圍內，觀測值曲線在理論期望值曲線之下，兩者之間存在相互離散關系，在420～500 m范圍內，觀測值曲線在理論期望值曲線之上，位于蒙特卡羅模擬置信區間之內.在500～3 500 m范圍內，觀測值曲線位于蒙特卡羅模擬置信區間上限之外，說明兩者之間存在顯著性的空間聚集關系.在0～4 000 m范圍內，體育中心街道體育設施和餐飲設施觀測值曲線在理論期望值曲線之上，位于蒙特卡羅模擬置信區間上限之外，說明體育設施和餐飲店之間存在顯著性的空間聚集關系.在0～3 500 m范圍內，柳林街道體育設施和餐飲設施觀測值曲線在理論期望值曲線之上，位于蒙特卡羅模擬置信區間上限之外，說明體育設施和餐飲店之間存在顯著性的空間聚集關系.由上述分析可知，體育設施熱點區域的分布和居民小區不具有顯著性聚集的空間關系.體育設施熱點區域的分布與公交站點在較大尺度下有聚集性，空間分布相似，受其影響較大.體育設施熱點區域的分布與餐飲設施具有顯著的空間聚集性，相互之間影響較大.體育設施熱點分布區對交通和餐飲具有空間依附性.

圖1 天津市體育中心街道與柳林街道設施點網絡雙變量K函數分析

4 結 論

本研究對天津市中心城區體育設施POI數據，采用網絡核密度和帶有權重的平面核密度相結合的分析方法，分析體育設施點在權重和道路網絡約束下空間分布的聚集區域.采用雙變量網絡K函數方法研究影響體育設施熱點區域分布的主要因素.分析表明，天津市中心區體育設施的空間分布具有“西南密東北疏”的分布特征，并且熱點區域呈現多中心點聚集.其中網絡核密度聚集較高的密度區有體育中心街道，柳林街道，學府街道，天塔街道.網絡核密度和帶有權重的平面核密度相結合的方法，能夠準確的表達設施點的自身影響力在道路網下的空間分布，這是傳統核密度方法所不能達到的.通過對體育中心街道和柳林街道熱點區域的網絡K函數分析方法探知，體育設施對交通和餐飲具有空間依附性.本研究對體育設施的空間分布的合理性，協調性具有一定的參考.在道路網絡的參考中，并沒有考慮道路的方向性，通行力等因素，對網絡的約束能力的表達還不完整，將在今后的研究中進行更加深入的探討.