基于滑動窗口LSTM網絡的船舶航跡預測

王余寬 謝新連 馬昊 潘偉 許小衛

摘要：為準確預測復雜水域船舶航跡，提高航行安全水平，提出一種基于滑動窗口長短期記憶（long short-term memory， LSTM）網絡的船舶航跡預測方法。根據相鄰航跡點的船位特征變化趨勢，剔除異常數據，并利用插值方式填補缺失點船位數據，建立船舶航行狀態數據庫。根據船舶航向變化態勢建立航行狀態判別準則，識別船舶航行場景。考慮船位信息特征維度高的特點，應用LSTM網絡理論構建基于滑動窗口LSTM網絡的船舶航跡預測模型。應用大連港水域和黃渤海水域的AIS數據，分別在不同航行場景下進行驗證。結果表明：直航型、轉向型和‘S’型場景下，滑動窗口LSTM網絡預測結果的平均絕對百分比誤差、均方誤差和均方根誤差均比基礎LSTM網絡、反向傳播神經網絡和灰色模型的小，這表明滑動窗口LSTM網絡對非線性航跡預測的泛化能力強于其他3種模型。

關鍵詞：

船舶航跡預測; 長短期記憶（ LSTM）網絡; 滑動窗口

中圖分類號： U675.7

文獻標志碼： A

Ship trajectory prediction based on sliding window LSTM network

WANG Yukuan1，2， XIE Xinlian1， MA Hao1， PAN Wei1， XU Xiaowei1

（1. Integrated Transport Institute， Dalian Maritime University， Dalian 116026， Liaoning， China;

2. School of Navigation， Wuhan University of Technology， Wuhan 430070， China）

Abstract：

In order to accurately predict ship trajectory in complex waters and improve the level of navigation safety， a method of ship trajectory prediction is proposed based on the sliding window long short-term memory （LSTM） network. According to the change trend of ship position characteristics of the neighboring trajectory points， the abnormal data are eliminated， the missing ship position data are filled by interpolation， and then a ship navigation state database is established. The navigation state discriminating criteria are established to identify the ship navigation scenarios based on the ship heading change situation. Considering the high dimensionality of ship position information， a ship trajectory prediction model based on the sliding window LSTM network is built by LSTM network theory. The AIS data of Dalian Port， Huanghai Sea and the Bohai Sea waters are used to carry out the verification in different navigation scenarios. The results show that the mean absolute percentage error， mean square error and root mean square error of the sliding window LSTM network prediction results are smaller than those of the basic LSTM network， the back propagation neural network and the grey model in straight， steering and S-type scenarios， indicating that the generalization ability of the sliding window LSTM network for nonlinear trajectory prediction is stronger than the other three models.

Key words：

ship trajectory prediction; long short-term memory （LSTM） network; sliding window

0 引 言

隨著現代水上航行環境復雜程度的提高，船舶航行風險增加，特別是在船舶密集水域、施工水域，干擾船舶安全航行的因素更多。準確預測船舶航跡可以幫助操船人員提前識別航行風險，提高船舶航行安全水平。因此，研究如何有效利用船舶航行歷史數據，提高航跡預測精度，對于保障船舶航行安全具有重要意義。

船舶航跡預測方法主要包括兩類：基于航跡相似度測量的方法和基于神經網絡理論的方法。從航跡相似度測量的角度開展的航跡預測研究主要有：ZHANG等[1]建立了一個港口間歷史軌跡數據庫，利用隨機森林模型測量船舶航跡與數據庫航跡的相似性來預測船舶航行行為;MURRAY等[2] 和GAO等[3]應用無監督學習方法對船舶歷史航跡進行聚類，然后對船舶未來航跡或操縱行為模式進行預測;HAO等[4] 、ZHANG等[5]和PALLOTTA等[6]測量了航跡間相似度，然后獲取了船舶在各水域出現概率的分布特征;DE VRIES等[7]對船舶航跡數據進行了聚類、分類以及離群檢測等;ZHANG等[8]利用具有噪聲的基于密度的空間聚類方法 （density-based spatial clustering of applications with noise，DBSCAN）確定了船舶轉彎節點并加以連通，從而推導出船舶航行模式;ZHOU等[9] 和周世波等[10]研究了港口水域內船舶航速等特征的變化態勢，揭示了一些船舶行為模式的整體性特征。基于神經網絡理論開展的航跡預測研究主要有：LIU等[11] 和任宇翔等[12]基于長短期記憶（long short-term memory，LSTM）網絡模型對非線性船舶航行行為進行預測，并強調模型輸入向量維度選取的重要性;胡玉可等[13]用基于對稱分段路徑距離的方法對船舶自動識別系統（automatic identification system，AIS）數據進行預處理，應用循環神經網絡預測航跡;SUO等[14]提出一種引入門循環單元模型的深度學習框架來預測航跡，并強調消除冗余數據影響的重要性;ZHOU等[15]、徐婷婷等[16]和游蘭等[17]采用船舶航行狀態區間差值思想，應用神經網絡模型建立船舶航跡預測模型;KIM等[18]考慮船舶交通服務中的情境規則，基于深度學習技術對船舶航行行為進行預測。一些學者采用支持向量機等技術開展了航跡預測研究，比如：NIE等[19]結合支持向量回歸和經驗模態分解方法，建立航跡短期預測模型;劉嬌等[20]用差分進化算法改進支持向量機構建航跡預測模型;謝新連等[21]考慮船舶轉向或變速行為，建立了極限學習機航行行為預測模型;ZHANG等[22]利用拉格朗日模型研究了海洋氣象環境數據對虛擬漂移器軌跡預測的影響;PERERA[23]基于矢量乘積的算法預測未來短時間內船舶的位置和航向。

上述文獻為預測船舶航跡提供了較多思路，但是對以下兩個方面考慮較少：一是原始AIS數據存在大量的噪聲和冗余，對AIS數據的預處理是航跡預測的關鍵;二是航跡預測有效步長較短，在保證航跡預測精度的同時提高預測步長，對提高船舶跟蹤精度和監管效率有重要作用。

本文構建一種基于AIS數據和LSTM網絡的航跡預測方法。在AIS數據處理部分，根據相鄰航跡點的船位特征變化剔除船舶異常數據，并利用插值方式補齊缺失的船位信息，然后基于對航向變化態勢的分析對船舶航行場景進行識別。在航跡預測部分，應用LSTM網絡理論提出基于滑動窗口LSTM網絡的預測模型，然后給出航跡預測質量評價標準。最后，對直航型、轉向型和‘S’型等3種典型的航行場景進行航跡預測實例分析。

1 AIS數據處理

1.1 數據清洗

航跡預測需要足夠多的AIS數據，數據質量對模型預測精度也會有很大影響。然而，受信號干擾、AIS設備使用錯誤等因素影響，接收到的AIS數據中存在著大量的噪聲數據，如船舶位置（經緯度）異常、速度異常和航向異常等。在使用AIS數據之前，需要辨識數據中的異常值，然后剔除異常數據并對缺失數據進行補全。

通常情況下，船舶狀態在短時間內不會發生較大變化，因此可根據相鄰航跡點的船位特征識別異常值。選取經度、緯度、航速和航向為船位特征，設定該航段發生時間內相鄰船位特征差值的最大值為空間變化閾值。

用llon，j、llat，j、υj和χj分別表示第j個航跡點的經度、緯度、航速和航向，用δlon、δlat、δυ和δχ分別表示經度、緯度、航速和航向的空間變化閾值，用

[WTHX]Φ[WTBX]j表示第j個航跡點的船位特征向量，

[WTHX]Φ[WTBX]j=（llon，j，llat，j，υj，χj）。計算第j個航跡點與第j+1個航跡點的船位特征差值，當這兩點的任一船位特征差值的絕對值大于相應船位特征的空間變化閾值時，判定第j個航跡點為異常點，并剔除該點數據。

如果被剔除的航跡點不是邊界點，則采用插值方式[24]對該點動態信息進行補全。如果被剔除的航跡點是邊界點，則不再補全（因為對其進行插值缺少足夠的條件）。根據被剔除航跡點前后船位點的經度、緯度、航速和航向等船位特征補全航跡點信息，公式如下：

Φj=Φj-k+（Φj+m-Φj-k）（tj-tj-k）tj+m-tj-k

式中：tj表示缺失點對應的時刻;Φj、Φj+m和Φj-k分別表示缺失點、缺失點前第m點和缺失點后第k點的船位特征信息。

將處理過的AIS數據依據船舶海上移動業務識別碼（maritime mobile service identity， MMSI）建立水域內各船舶航跡信息數據庫。船舶航跡信息示例見表1。

許偏移值;μ為變向加速度發生突變的閾值。當χ′j≤ε時ψ=1，即將船舶航向單位時間內改變非常小的情況視作船舶未進行轉向（處于直航型航行場景）。而當χ′j>ε時，若始終有χ″j≤μ，則視船舶保持一定的變向速率（處于轉向型航行場景）。對于‘S’型航行場景的判別，則需滿足χ′j>ε，且存在n∈{1，2，…，J}使得χ″n>μ。

ε的確定方法為：統計所有直航型航跡上各航跡點處變向速率的絕對值，取其最大值并向上取整即得ε值。根據實驗統計，若船舶為速度較快的引航艇或海巡船等類型船舶，則設置ε=3;若船舶為客船或貨船，相鄰AIS數據傳回時間間隔內船舶航跡不會發生較大偏移，則設置ε=2。μ的確定方法為：統計所有轉向型航跡上各航跡點處變向加速度的絕對值，取其最大值并向上取整即得μ值。根據仿真實驗設置μ=2。

2 基于滑動窗口LSTM網絡的船舶航跡預測模型

2.1 滑動窗口LSTM網絡

LSTM網絡可以存儲遠程時間依賴性信息，并且可以在輸入數據與輸出數據之間進行適當映射，在時間序列數據預測方面功能強大[25]。LSTM網絡結構不同于傳統的感知器體系結構，它包含1個內部狀態存儲單元和3個控制信息流的門（輸入門、遺忘門和輸出門）[25]。

本文應用LSTM網絡理論提出一種基于滑動窗口LSTM網絡的預測模型。考慮到船位差更能體現船位變化趨勢，用船位差作為預測模型的輸入變量進行航跡預測。為便于計算，以船舶初始航跡點為基準坐標，采用墨卡托投影坐標轉換將船位坐標從大地坐標系轉換到平面直角坐標系，

第j個航跡點在平面直角坐標系中的坐標表示為（xj，yj），某航段航跡點在平面直角坐標系中的坐標集合表示為P={（xj，yj）j=1，2，…，J}。船位差序列包含航跡點之間的時間差序列以及船舶沿X方向和Y方向的坐標值差序列，分別用ΔT和ΔP表示：式中：t1和tj+1為分別第1和j+1個航跡點對應的時刻;ΔTj為第j個航跡點與第1個航跡點之間間隔的時間;ΔPj為第j個航跡段的船位差序列;ΔXj和ΔYj分別為第j個航跡段的船位差在X軸和Y軸上的投影。

假設可獲得的船位數據的數量為Q，設定滑動窗口長度為N，滑動窗口長度即為每次訓練輸入船位數據

的長度。LSTM網絡每次訓練輸出一個預測船位數據，并采用“去舊補新”模式迭代更新滑動窗口中的船位數據，即用訓練輸出值作為最新數據替換滑動窗口中的最舊數據。滑動窗口LSTM網絡迭代進行Q-N次訓練，不斷優化參數獲得航跡預測模型。滑動窗口LSTM網絡訓練結構見圖2。

在進行模型訓練時，將船位差序列分組，每

組包含從S1到SN+1共N+1個船位差數據;以前N個船位差數據（S1～SN）作為輸入，經LSTM網絡訓練輸出第N+1個船位差數據S′N+1，并與第N+1個船位差數據真實值SN+1進行對比;通過輸出數據的誤差分析迭代調整LSTM網絡參數，最終獲得LSTM預測模型。在進行LSTM網絡訓練時，遺忘門f（ti）將ΔTi和ΔPi-1作為輸入，計算得到sigmoid激活信息;輸入門a（ti）取ΔTi和ΔPi-1來計算c（ti）的值;輸出門o（ti）通過sigmoid和tanh函數來調節LSTM單元的輸出。

2.2 滑動窗口LSTM網絡預測模型

在進行航跡

預測時，利用第Q-N至Q個船位數據預測未來第Q+1個船位數據，再由第Q-N+1至Q+1個船位數據預測第Q+2個船位數據，直至預測到未來第Q+M個船位數據;而在滑動預測過程中，如果真實的船舶數據繼續被接收且在時間上覆蓋了已預測數據，則使用最新的真實數據替換預測值作為模型輸入數據。滑動窗口LSTM網絡預測模型見圖3。

由船位差序列方程預測未來M個時刻的船舶位置時，用ΔTh，j和ΔPh，j分別表示歷史第j個航跡段兩端航跡點的時間差和船位差，將所求歷史時間差序列ΔTh、船位差序列ΔPh和未來M個時刻對應的時間差序列ΔTp作為輸入數據，數據方程如下：

2.3 模型評價標準

為評價滑動窗口LSTM網絡模型的航跡預測性能，定義“船位相對誤差”（relative error of ship position，ERSP）為船位誤差與各船位到基準點距離平均值的比值，用百分比形式表示，其值越小表示預測航跡點偏離實際航跡的程度越小。船位相對誤差用于評價模型對單個航跡點預測的準確性。另外，采用基于船位信息的平均絕對百分比誤差（mean absolute percentage error，EMAP）、均方誤差（mean square error，EMS）和均方根誤差（root mean square error，ERMS）等多個指標評估模型對趨勢預測的穩定性。EMAP將航跡預測結果偏離程度表示為百分比形式;EMS表示航跡點坐標預測的平均誤差;ERMS表示模型預測結果的標準偏差。4個評價指標值越小表明模型預測準確性越高，計算式分別如下

式中：xr，j和yr，j分別為未來第j時刻船舶航跡點沿X方向和Y方向的實際坐標值;xr，1和yr，1分別為未來第1時刻航跡點沿X方向和Y方向的實際坐標值。

3 實例分析

利用AIS設備在遼寧省大連市周邊多個海域接收船舶航行數據，編碼識別1 000艘次以上船舶的AIS信息。對AIS數據進行清洗，然后利用第1.2節的方法識別并選出處于直航型、轉向型和‘S’型航行場景下的船舶各1艘進行航跡預測。選出的3種典型航行場景下的船舶信息見表2。

對3種典型航行場景下的船舶進行航跡預測時，所構建的訓練集和測試集數據比例約為4∶1。關于訓練和測試過程中的樣本分配，以直航型航行場景為例加以說明。訓練部分：樣本總量Q1為80，以77個時刻的航跡數據（SQ-79，SQ-78，…，SQ-3）為滑動窗口LSTM網絡的輸入數據，以對應延后3個時段的航跡數據（SQ-76，SQ-75，…，SQ）為滑動窗口LSTM網絡的輸出數據，訓練后保存模型參數。測試部分：樣本總量Q2為23，以連續20個時刻的船舶航行動態序列數據（SQ-22，SQ-21，…，SQ-3）為測試

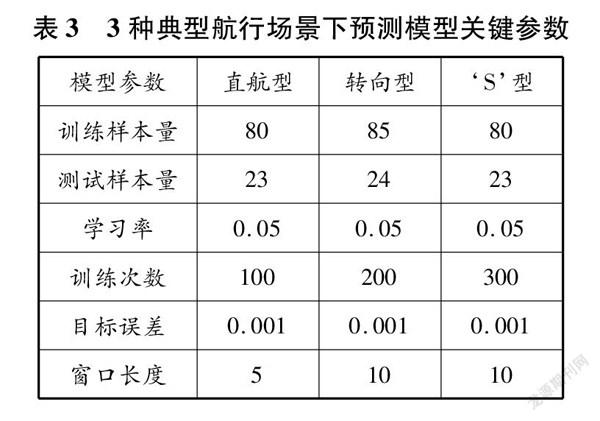
滑動窗口LSTM網絡的輸入數據，來預測船舶航跡數據（SQ-19，SQ-18，…，SQ）。另外，窗口長度值代表訓練序列的輸入長度，其值會影響訓練迭代時間和預測精度。為避免迭代過程中模型學習時間過長，設置窗口長度閾值上界為15，根據樣本量大小設置閾值下界為4。分別對3種典型航行場景，在窗口長度閾值范圍[4，15]內搜索最優窗口長度值。根據重復實驗結果，當直航型、轉向型和‘S’型航行場景下的窗口長度分別為5、10和10時模型達到訓練目標誤差時的訓練時長最短。3種典型航行場景下預測模型關鍵參數見表3。

表3

模型的損失值會隨訓練過程變化，因此模型訓練的次數會影響具有固定架構的LSTM網絡模型的性能。由圖4可知：隨著訓練次數的增加，模型的均方根誤差先增大后減小;在訓練達到30次后，均方根誤差基本趨于穩定，訓練效果較好。在轉向型和‘S’型兩種航行場景下，在表3所示的訓練次數范圍內模型的均方根誤差亦能達到穩定。

用同樣的訓練集和測試集對基礎LSTM網絡、一階灰色模型GM（1，1）和反向傳播神經網絡（back propagation neural network， BPNN）進行實驗，并將各種模型的預測效果進行對比。基礎LSTM網絡的參數設置同滑動窗口LSTM網絡。一階灰色模型的發展系數取值為0.5。基于文獻[16]對BPNN進行參數選優，輸入層和輸出層神經元個數均取2，隱含層神經元個數取10。3種典型航行場景下不同模型對測試航跡點的預測結果見圖5，其中用“SL-LSTM”代表滑動窗口LSTM網絡，用“LSTM”代表基礎LSTM網絡。由圖5可知：在直航型航行場景下，各種模型預測的航跡偏離程度均較低;在轉向型和‘S’型航行場景下，隨著預測航跡點數量的增加，滑動窗口LSTM網絡預測結果仍較為接近實際航跡，基礎LSTM網絡預測結果逐漸偏離實際航跡，而GM（1，1）和BPNN預測結果出現較大偏差。

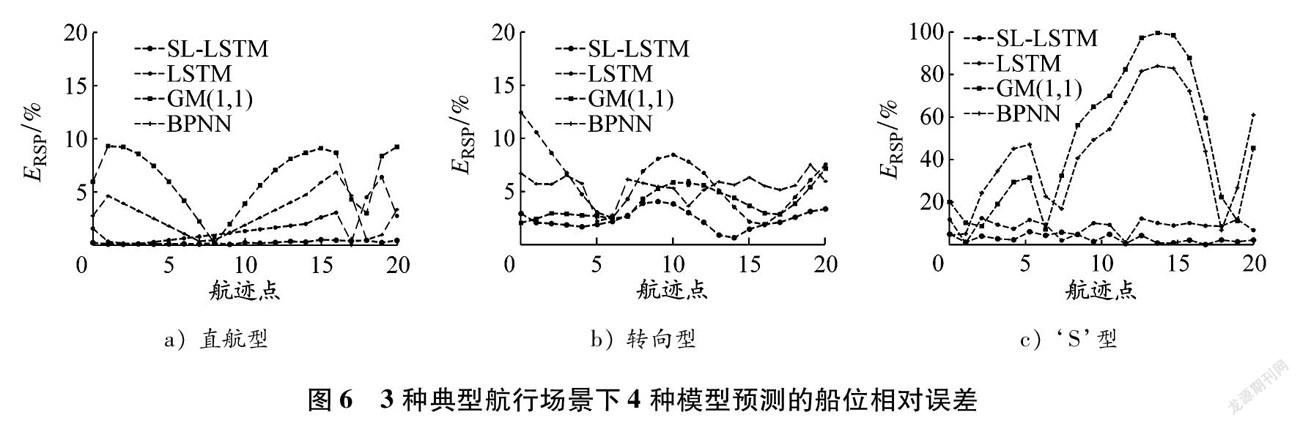
分析對單個航跡點預測的準確性，圖6給出了3種典型航行場景下4種模型預測的各個航跡點的船位相對誤差（ERSP）。由6可以看出：在直航型航行場景下，4種模型預測的ERSP均在10%以內，滑動窗口LSTM網絡預測的ERSP始終保持在1%以下，基礎LSTM網絡和BPNN預測的ERSP隨著航跡點數量

的增加而逐漸增大，GM（1，1）預測的ERSP波動最大;在轉向型航行場景下，滑動窗口LSTM網絡預測的ERSP在5%以內，GM（1，1）和BPNN預測的ERSP則在3%～10%范圍內，基礎LSTM網絡預測的絕大多數航跡點的ERSP均在10%以內，僅兩個航跡點的ERSP超過10%;在‘S’型航行場景下，基礎LSTM網絡預測的ERSP在10%左右，BPNN和GM（1，1）預測的ERSP已經出現極大波動，對部分航跡點預測的ERSP超過50%，滑動窗口LSTM網絡對大部分航跡點預

測的ERSP在0～5%范圍內，僅對3個航跡點預測的ERSP超過5%（且低于10%）。

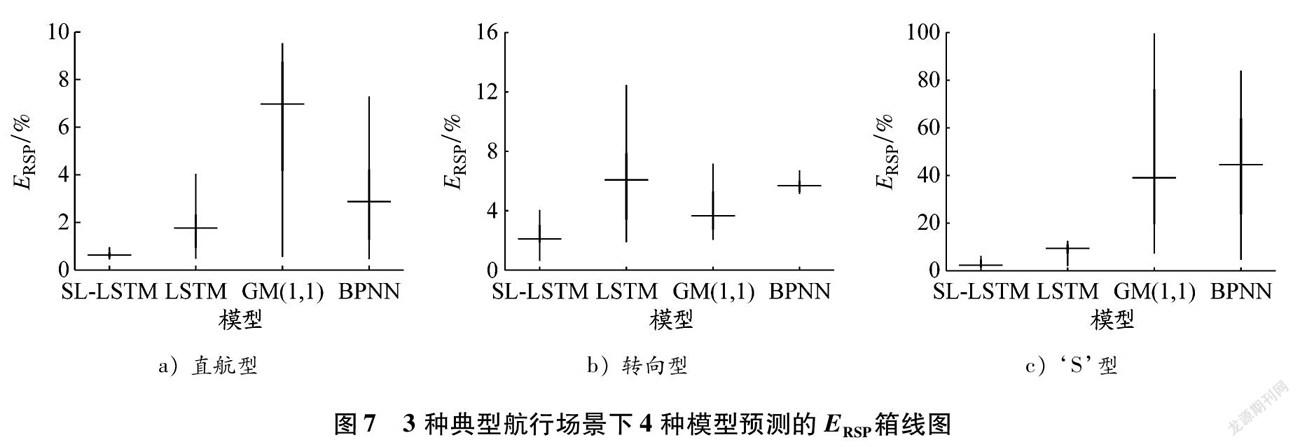
圖7展示了3種典型航行場景下4種模型預測的ERSP總體分布。在直航型和‘S’型航行場景下，滑動窗口LSTM網絡和基礎LSTM網絡的預測表現明顯優于BPNN和GM（1，1）的;在轉向型航行場景下，基礎LSTM網絡的預測表現同BPNN的，但劣于GM（1，1）的。由圖6和7可知，在3種典型航行場景下，滑動窗口LSTM網絡均可提供較為準確的單點預測，預測效果均優于其他3種模型的，BPNN和GM（1，1）在直航型和轉向型航行場景下的表現尚可，基礎LSTM網絡在直航型和‘S’型航行場景下的預測表現良好。

為進一步量化模型的預測性能，計算出4種模型對相同測試集進行實驗的平均絕對百分比誤差（EMAP）、均方誤差（EMS）和均方根誤差（ERMS），見表4。由表4可知：直航型、轉向型和‘S’型航行場景下滑動窗口LSTM網絡預測的EMAP分別為0.176%、2.386%和2.927%，均遠比其他模型的小，表明該模型預測準確性較高;滑動窗口LSTM網絡預測的EMS和ERMS較小，表明該模型比其他3種模型穩定;在直航型和轉向型航行場景下，基礎LSTM網絡與BPNN預測結果的EMAP、EMS和ERMS均較為接近;在‘S’型航行場景下，GM（1，1）和BPNN在各項評價指標上表現都很差。

綜上可知，不同航行場景下滑動窗口LSTM網絡的各類預測誤差值均比其他3種模型的小，這表明本文提出的滑動窗口LSTM網絡不僅可以更好地預測船位整體變化趨勢，而且在較長時間內對單個航跡點的預測結果偏離實際的程度較低，提高了航跡預測的準確性。而基礎LSTM網絡，盡管在整體變化趨勢的預測上表現尚可，但隨著航跡點數量的增加該模型對單個航跡點的預測誤差逐漸增大。

4 結束語

為提升目標水域船舶通航情況的監管效率，降低船舶航行風險，提出基于滑動窗口LSTM網絡的航跡預測方法。結論如下：（1）針對船舶AIS數據存在異常的問題，基于對船位特征的空間變化閾值分析對離群點進行識別，剔除并補全相應航跡點數據，進而建立船舶航行狀態數據庫。基于船舶航向變化趨勢建立的航行場景識別方法，可以作為表達船舶航跡特征的有效方法。（2）利用LSTM網絡對時間序列數據預測性能良好的優勢，建立基于滑動窗口LSTM網絡的航跡預測模型。

滑動窗口LSTM

網絡對直航型、轉向型和‘S’型航跡預測的平均絕對百分比誤差分別為0.176%、2.386%和2.927%，均遠小于基礎LSTM網絡、BPNN和GM（1，1）的預測誤差。另外，滑動窗口LSTM網絡預測的均方誤差和均方根誤差均較小，表明滑動窗口LSTM網絡比其他3種模型穩定。在直航型、轉向型和‘S’型3種典型航行場景下，滑動窗口LSTM網絡不僅可以準確預測航跡變化趨勢，而且對單個航跡點預測的偏離程度也很低，其表現明顯優于基礎LSTM網絡、BPNN和GM（1，1）。

由于滑動窗口LSTM網絡的航跡預測對數據量有一定的要求，未來研究中對于數據量較少的情況需要采用插值等方法增大數據量。本文提出的方法僅能對已經安裝了AIS設備的船舶進行航跡預測，未來可考慮融合雷達等多源信息，以實現對水域內所有船舶的監管。

參考文獻：

[1]ZHANG C K， BIN J C， WANG W， et al. AIS data driven general vessel destination prediction： a random forest based approach[J]. Transportation Research Part C， 2020， 118： 102729. DOI： 10.1016/j.trc.2020.102729.

[2]MURRAY B， PERERA L P. A dual linear autoencoder approach for vessel trajectory prediction using historical AIS data[J]. Ocean Engineering， 2020， 209： 107478. DOI： 10.1016/j.oceaneng.2020.107478.

[3]GAO M， SHI G Y. Ship-handling behavior pattern recognition using AIS sub-trajectory clustering analysis based on the T-SNE and spectral clustering algorithms[J]. Ocean Engineering， 2020， 205： 106919. DOI： 10.1016/j.oceaneng.2020.106919.

[4]HAO R， TEIXEIRA A P， SOARES C G. Ship trajectory uncertainty prediction based on a Gaussian process model[J]. Ocean Engineering， 2019， 182： 499-511. DOI： 10.1016/j.oceaneng.2019.04.024.

[5]ZHANG L Y， MENG Q. Probabilistic ship domain with applications to ship collision risk assessment[J]. Ocean Engineering， 2019， 186： 106130. DOI： 10.1016/j.oceaneng.2019.106130.

[6]PALLOTTA G， VESPE M， BRYAN K. Vessel pattern knowledge discovery from AIS data： a framework for anomaly detection and route prediction[J]. Entropy， 2013， 15： 2218-2245. DOI： 10.3390/e15062218.

[7]DE VRIES G K D， VAN SOMEREN M. Machine learning for vessel trajectories using compression， alignments and domain knowledge[J]. Expert Systems with Applications， 2012， 39： 13426-13439. DOI： 10.1016/j.eswa.2012.05.060.

[8]ZHANG S K， SHI G Y， LIU Z J， et al. Data-driven based automatic maritime routing from massive AIS trajectories in the face of disparity[J]. Ocean Engineering， 2018， 155： 240-250. DOI： 10.1016/j.oceaneng.2018.02.060.

[9]ZHOU Y， DAAMEN W， VELLINGA T， et al. Ship classification based on ship behavior clustering from AIS data[J]. Ocean Engineering， 2019， 175： 176-187. DOI： 10.1016/j.oceaneng.2019.02.005.

[10]周世波， 唐基宏， 熊振南. 基于優化模糊C均值算法的錨泊船聚集特性[J]. 交通運輸工程學報， 2019， 19（6）： 137-148. DOI： 10.19818/j.cnki.1671-1637.2019.06.013.

[11]LIU Y C， DUAN W Y， HUANG L M， et al. The input vector space optimization for LSTM deep learning model in real-time prediction of ship motions[J]. Ocean Engineering， 2020， 213： 107681. DOI： 10.1016/j.oceaneng.2020.107681.

[12]任宇翔， 趙建森， 劉衛， 等. 基于AIS數據和LSTM網絡的船舶航行動態預測[J]. 上海海事大學學報， 2019， 40（3）： 32-37. DOI： 10.13340/j.jsmu.2019.03.006.

[13]胡玉可， 夏維， 胡笑旋， 等. 基于循環神經網絡的船舶航跡預測[J]. 系統工程與電子技術， 2020， 42（4）： 871-877. DOI： 10.3969/j.issn.1001-506X.2020.04.18.

[14]SUO Y F， CHEN W K， CLARAMUNT C， et al. A ship trajectory prediction framework based on a recurrent neural network[J]. Sensors， 2020， 20： 5133. DOI： 10.3390/s20185133.

[15]ZHOU H， CHEN Y J， ZHANG S M. Ship trajectory prediction based on BP neural network[J]. Journal on Artificial Intelligence， 2019， 1（1）： 29-36. DOI： 10.32604/jai.2019.05939.

[16]徐婷婷， 柳曉鳴， 楊鑫. 基于BP神經網絡的船舶航跡實時預測[J]. 大連海事大學學報， 2012， 38（1）： 9-11. DOI： 10.16411/j.cnki.issn1006-7736.2012.01.028.

[17]游蘭， 韓雪薇， 何正偉， 等. 基于改進Seq2Seq的短時AIS軌跡序列預測模型[J]. 計算機科學， 2020， 47（9）： 169-174. DOI： 10.11896/jsjkx.190800060.

[18]KIM K I， LEE K M. Context-aware information provisioning for vessel traffic service using rule-based and deep learning techniques[J]. International Journal of Fuzzy Logic and Intelligent Systems， 2018， 18（1）： 13-19. DOI： 10.5391/IJFIS.2018.18.1.13.

[19]NIE Z H， SHEN F， XU D J，et al. An EMD-SVR model for short-term prediction of ship motion using mirror symmetry and SVR algorithms to eliminate EMD boundary effect[J]. Ocean Engineering， 2020， 217： 107927. DOI： 10.1016/j.oceaneng.2020.107927.

[20]劉嬌， 史國友， 楊學錢， 等. 基于DE-SVM的船舶航跡預測模型[J]. 上海海事大學學報， 2020， 41（1）： 34-39， 115. DOI： 10.13340/j.jsmu.2020.01.006.

[21]謝新連， 陳紫薇， 魏照坤， 等. 基于極限學習機的船舶航行行為預測[J]. 重慶交通大學學報（自然科學版）， 2019， 38（8）： 7-12， 123. DOI： 10.3969/j.issn.1674-0696.2019.08.02.

[22]ZHANG X D， CHENG L， ZHANG F L， et al. Evaluation of multi-source forcing datasets for drift trajectory prediction using Lagrangian models in the South China Sea[J]. Applied Ocean Research， 2020， 104： 102395. DOI： 10.1016/j.apor.2020.102395.

[23]PERERA L P. Navigation vector based ship maneuvering prediction[J]. Ocean Engineering， 2017， 138： 151-160. DOI： 10.1016/j.oceaneng.2017.04.017.

[24]王小凱， 朱小文. 計量檢定中3種判別和剔除異常值的統計方法[J]. 中國測試， 2018， 44（增刊1）： 47-50.

[25]CAI J X， HU J L， TANG X， et al. Deep historical long short-term memory network for action recognition[J]. Neurocomputing， 2020， 407： 428-438. DOI： 10.1016/j.neucom.2020.03.111.

（編輯 賈裙平）

收稿日期： 2020-12-05

修回日期： 2021-10-14

基金項目：

國家重點研發計劃（2017YFC0805309）;中央高校基本科研業務費專項資金（3132019303）

作者簡介：

王余寬（1995—），男，河南周口人，博士研究生，研究方向為交通信息工程及控制，（E-mail）wangyk_321@163.com;

謝新連（1956—），男，遼寧大連人，教授，博導，博士，研究方向為交通運輸規劃與管理、船舶工程與經濟，

（E-mail）xxlian@dlmu.edu.cn