探討圓弧導線電勢的計算
王悅 劉宇 吳志豪 李南 王嵐 何碧蕓 方碧綠 梁靖琪 古俊 胡新春
(銅陵學院 安徽銅陵 244000)
靜電場中,能夠反映其本質的物理量是電場強度和電勢,因而,電場強度的計算和電勢的計算成了研究靜電場特性和教師教學中的重點和難點[1-3]。靜電場中,帶電體的電勢計算可以分成兩大類,即電勢疊加法和電勢定義法。有限帶電體電勢的計算方法很多[4-6]。
1 電勢計算舉例
以一段圓弧均勻帶電體為例,用不同方法進行求解。如圖1所示,一個半徑為R的均勻帶電圓弧,圓心角為α,x軸平分α角,電荷線密度為λ,求弧心處的電勢V。

圖1 一段圓弧均勻帶電導線模型
2 用電勢疊加原理
2.1 疊加法
電勢疊加原理是利用點電荷的電勢求解任意帶電體在空間產生的總電勢。取無窮遠為勢能零點時,點電荷q在r處產生的電勢為:
具體計算時,可以用式(1)求出電荷元產生的電勢,再用疊加法求解總電勢。
疊加法是由點電荷電勢作為微元,通過積分,算出圓弧整體的電勢。
對有限大的帶電體取無窮遠為勢能零點時,點電荷q在距離點電荷為R處的電勢可以寫成下式:
如圖2所示,電荷元dq在O點產生的電勢為:

圖2 取電荷元分析
則積分整個圓弧可以得到弧心處電勢為:
2.2 挖補法
挖補法是由點電荷電勢作為微元,通過積分,算出一個整圓電勢,再求出圓弧的電勢。
如圖3所示,電荷元dq在O點產生的電勢為:
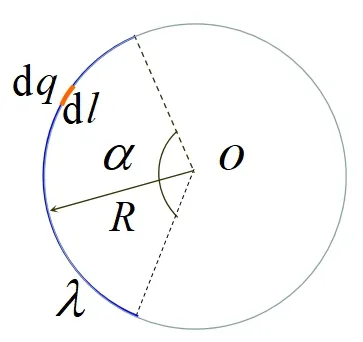
圖3 挖補法求解圖
那么,一個完整個圓環帶電體O點產生的電勢:
由角度為α時占整個圓的比例為α/2π,所以,圓弧在O點產生的電勢為:
此結論與式(4)結果一致。
上述兩種方法實質上都是采用電勢的疊加原理,只是一種是先整體再局部,一種是從局部直接出發積分計算,其難易程度相當。
3 用場強積分方法
3.1 電勢與電場強度的關系
由于靜電場中某點的電勢大小等于單位正電荷置于該點時的電勢能,也等于單位正電荷,從該點經任意路徑移到電勢零點時,電場力所做的功出發,若試驗電荷的電量為q0,根據電勢的定義,a點處的電勢Va等于電勢能Wa與電量q0的比,即:
式(8)是電勢的定義式,電勢也叫電位。
由式(9)可見,電勢可以通過電場強度積分路徑求出。
電勢是相對的,是標量,其大小與參考點的選取有關,原則上電勢為零的參考點可以任意選取,但是,為了研究方便,一般對電荷分布為有限空間時,零參考點取在無窮遠處。對于現在分析的一段圓弧,選取無窮遠為勢能零點,先算出空間從O點到無窮遠的電場,再通過電場強度大小積分算出O點電勢。
3.2 場強積分法
如圖4所示,取x軸上任意一點P作為研究位置,dq在P點產生的電場為:

圖4 場強積分法求解
由圖中的幾何關系可得:
所以有:
而總場為兩倍x方向分量電場大小,從而得到總場的微分表達式為:
進而可以積分得到電場強度大小為:
當x?R時,r=x+R,可得:
方向為x軸正方向。
4 結語
很容易看出式(4)、式(7)、式(16)的結論完全一致,可以用3 種不同計算方法求解同一個具體的物理問題。通過分析,可以發現,對于求解帶電體在空間激發電場產生的電勢,電勢疊加原理和電勢定義是通過電場強度的線積分求解,兩種方法本質上都能計算。但是,同一問題往往難易程度相差很大,所以,計算不同帶電體的電勢要有針對性地選擇合適方法。對于幾何對稱性好的,可以用電勢疊加法,與場強積分方法相比在計算過程簡化很多;對于沒有對稱性的,就只能用場強積分計算。這種一題多解的講解方式能夠使學生對類似問題了解得更清晰,能使學生更深刻地認識到電勢的計算過程,有利于提高學生用已學知識解決實際問題的能力。

