基于雙目標優化的高速鐵路列車運行調整

閆 璐，張 琦，丁舒忻，王榮笙,

（1. 中國鐵道科學研究院研究生部，北京 100081；2. 中國鐵道科學研究院集團有限公司通信信號研究所，北京 100081；3. 中國鐵道科學研究院集團有限公司國家鐵路智能運輸系統工程技術研究中心，北京 100081）

高速鐵路列車運行存在“高密度”的特征［1］，一旦受到突發事件影響，往往會引發列車晚點，并在線路和路網中傳播，情況嚴重時會給運輸組織和旅客正常出行造成極大影響。根據晚點的原因和程度，可將引發晚點的內外界擾動分為2 種類型：一種是一般干擾，如旅客乘降作業超時等；另一種是嚴重干擾，如因風、雨、雪等自然災害或設備故障產生的長時間封鎖等［2］。無論哪種干擾，均將導致列車運行在一定程度上偏離既定計劃的后果，此時就需要進行列車運行調整。列車運行調整是實現“按圖行車”的關鍵，也是高速鐵路列車安全、高效、有序、正點運行的基礎［3］。

國內外眾多學者已對列車運行調整問題開展了大量研究［4-7］。現階段的研究通常考慮多個優化目標，其中減少列車總晚點時間多為主要目標，其他優化目標包括提高旅客滿意度、減少取消列車數量等。這些需要優化的目標之間往往互相沖突，需要權衡決策者對不同優化目標的偏好程度，從而得到不同的帕累托（Pareto）最優解。目前大部分研究采用前決策（a priori）的方式［8-14］，考慮決策者已經提供了全局偏好信息，在此基礎上搜尋該偏好下的一個Pareto 最優解。LI 等［8］針對車站股道封鎖不確定恢復時間，考慮最小化晚點成本和股道調整成本，建立混合整數非線性規劃模型，采用2 階段法求解，第1階段通過貪心算法求解列車調整后的到發時間和次序，并在該決策方案下采用遺傳算法調整車站股道，完成第2 階段求解。文獻［9—13］均考慮最小化取消列車趟數和總晚點時間，通過商用求解器CPLEX 或GUROBI 求解。WANG 等［14］針對初始晚點，以最小化列車總晚點時間和嚴重晚點列車趟數為優化目標，建立混合整數規劃模型，并提出遺傳算法結合粒子群算法的求解方法。目前大部分文獻都采用對不同優化目標線性加權的形式確定決策者偏好信息，這樣雖然不需要大量計算，但決策者的全局偏好信息并不能準確獲得。

還有部分研究采用后決策（a posteriori）方式，即先搜索整個Pareto前沿，再在該前沿中選擇最偏好的解。該方法并不需要知道決策者的全局偏好信息，而且可找到整個Pareto 前沿的近似解集，但需要很大的計算代價。SHAKIBAYIFAR 等［15］針對區間封鎖，以最小化列車終點站晚點時間和最小化列車發車運行偏差建立雙目標優化模型，采用多目標鄰域搜索算法求解。BINDER 等［16］針對車站存在多個股道封鎖，考慮最小化旅客不滿意度（換乘時間）、運營成本和調整成本，建立整數規劃模型，通過CPLEX 結合ε-約束法進行求解。ALTAZIN 等［17］針對列車晚點，考慮最小化恢復時間、旅客不滿意度（等待時間和車內時間）、調整操作（如取消車次、列車折返、增加停站、跳停等）總數、總晚點時間和晚點事件個數，采用啟發式方法求解并通過仿真進行評價。然而上述研究并未計算整個Pareto前沿，缺失了部分非支配解。

針對高速鐵路列車運行中的晚點情況，綜合考慮區間運行干擾和車站停車作業干擾，通過調整列車到發時刻和列車次序，以最小化列車總晚點時間和列車到發時刻調整次數為雙優化目標，建立高速鐵路列車運行調整的混合整數非線性規劃模型，并通過定義輔助矩陣將其轉化為線性規劃模型；提出改進的ε-約束法求解模型。通過算例以及加權法和先到先服務方法對比，驗證模型和求解算法。

1 優化模型

以最小化列車總晚點時間和最小化列車到發時刻調整次數為雙優化目標，以車站作業、區間運行、追蹤間隔等時間條件為約束條件，構建高速鐵路列車運行調整的雙目標優化模型。

1.1 模型假設

結合實際情況首先做如下假設：

（1）列車運行調整的方式包括調整列車到發時刻和列車次序；

（2）突發事件最終表征為列車在區間運行時和在車站停車作業時受到的干擾；

（3）車站均滿足接發車能力限制。

1.2 模型參數和決策變量定義

定義模型參數：i，l為列車編號；N為列車總數；j為車站編號；J為車站總數；k為區間編號；K為區間總數；τsij為列車i在車站j的圖定到站時刻；τeij為列車i在車站j的圖定發車時刻；αi為列車i的始發站車站編號；βi為列車i的終到或交出站車站編號；為列車i在車站j的最小作業時間（停站時間）；為列車i在區間k的最小運行時間；Ik為區間k的最小追蹤間隔時間；M為足夠大的正整數；為列車i在區間k受到干擾時增加的區間運行時間（區間運行干擾時間）；為列車i在車站j受到干擾時增加的車站停車作業時間（車站停車作業干擾時間）；為含有區間運行干擾的列車及對應的區間集合；為含有車站停車作業干擾的列車及對應的車站集合。

定義決策變量：xsij為列車i在車站j的實際到站時刻；xeij為列車i在車站j的實際發車時刻；qilk為0-1 決策變量，表示列車i和列車l在區間k的實際次序，當列車i先于列車l進入區間k時取值為1，否則取值為0。

1.3 目標函數

受到晚點影響后調度部門需要進行列車運行調整，使列車盡快恢復正點運行。對于受到影響的列車來說，在不同車站調整到發時間，會影響車站當前作業，增加相關作業人員負擔。因此，以最小化列車總晚點時間和最小化列車到發時刻調整次數為目標函數。

1）列車總晚點時間最少

定義列車總晚點時間等于運行調整之后所有列車到站時刻與圖定到站時刻的差值加上列車發車時刻與圖定發車時刻的差值，則列車總晚點時間最少的目標函數f1(x)可表示為

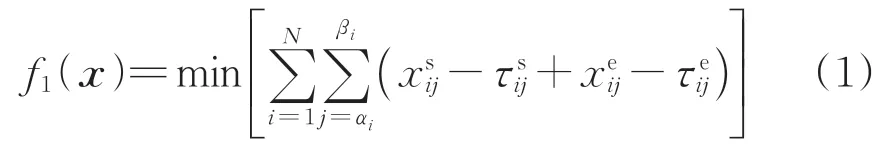
其中，

式中：x為實際到站時刻和實際發車時刻。

2）列車到發時刻調整次數最少

定義列車到發時刻調整次數等于所有列車到站和發車的總晚點次數，即晚點1次就需要調整1次，則列車到發時刻調整次數最少的目標函數f2(x)可表示為

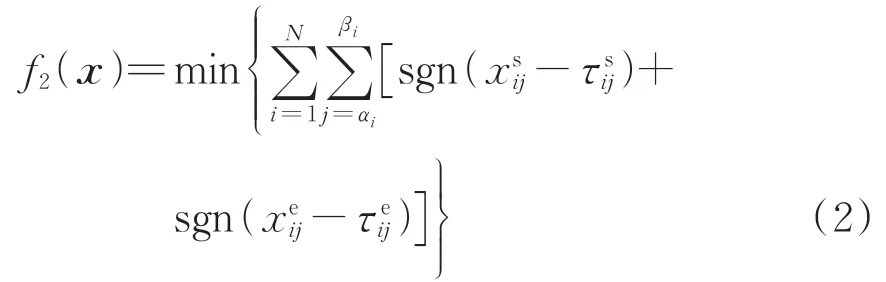
式中：sgn（·）為符號函數，返回對應參數的正負號（參數為0 則返回值為0），由于調整之后列車到站或發車時刻不允許早于圖定時刻，返回值不為負數，若調整后列車到站或發車時刻晚于圖定時刻，則返回值為1，記錄晚點1 次；若等于圖定時刻，則返回值為0，不記錄晚點次數。

1.4 約束條件

為了保證列車運行安全，合理利用接發列車能力、車站通過能力以及區間通過能力，建立的模型應滿足如下約束條件。

1）車站停站時間約束

列車i在車站j存在停車作業干擾時對運行圖的影響如圖1所示。圖中：黑色實線表示計劃運行線，對應停站時間為圖定停站時間；紅色虛線表示最小停站時間下的運行線；藍色虛線表示含有車站停車作業干擾時間下的運行線，此時列車停站時間在圖定停站時間基礎上增加干擾時間，該干擾時間為車站停站緩沖時間吸收之后的干擾時間。

圖1 車站停車作業存在干擾時對運行圖的影響

對于含有車站停車作業干擾的列車，調整之后的列車停站時間必須不小于該列車在該站的圖定停站時間與車站停車作業干擾時間之和；對于不含車站停車作業干擾的列車，調整之后的列車停站時間必須不小于該列車在該站的最小停站時間，即

式中：(i，j)∈Tdwell，dis和(i，j)?Tdwell，dis分別為含有、不含車站停車作業干擾的列車及對應的車站。

2）區間運行時間約束

列車i在區間k存在區間運行干擾時對運行圖的影響如圖2所示。圖中：黑色實線表示計劃運行線，對應區間運行時間為圖定運行時間；紅色虛線表示最小區間運行時間下的運行線；藍色虛線表示含有區間運行干擾時間下的運行線，此時列車區間運行時間在圖定運行時間基礎上增加的干擾時間，即為區間運行緩沖時間吸收之后的干擾時間。

圖2 區間運行時間存在干擾時對運行圖的影響

對于含有區間運行干擾的列車，調整之后的列車區間運行時間必須不小于該列車在該區間的圖定運行時間與區間運行干擾時間之和；對于不含區間運行干擾的列車，調整之后的列車區間運行時間必須不小于該區間的最小運行時間，即

式中：(i，k)∈Trun，dis和(i，k)?Trun，dis分別指含有、不含區間運行干擾的列車及對應的區間。

3）列車到發間隔時間約束

對于在同一區間內運行的相鄰列車，其到站和發車間隔時間必須不小于最小追蹤間隔時間，即

式中：∨和∧分別表示“或”和“且”，用于計算相鄰列車始發車站編號最大值和相鄰列車終到或交出車站編號最小值；qilk與qlik均為列車在區間次序的決策變量，二者取值不同，即qilk=1 時qlik=0，qilk=0時qlik=1。

4）列車到發時刻約束

列車在車站實際發車時刻必須不小于圖定發車時刻與停車作業干擾時間之和，實際到站時刻必須不小于圖定到站時刻與區間運行干擾時間之和，即

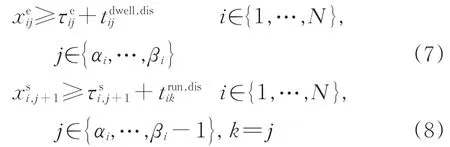
5）決策變量約束

列車實際到發時刻決策變量必須為非負變量，列車在區間的次序決策變量必須為0-1變量，即

1.5 模型處理

式（2）中存在sgn（·）符號函數，因此需要將其轉換為線性模型再進行處理。定義輔助矩陣c1=[c1，ij]N×J和c2=[c2，ij]N×J，賦值為

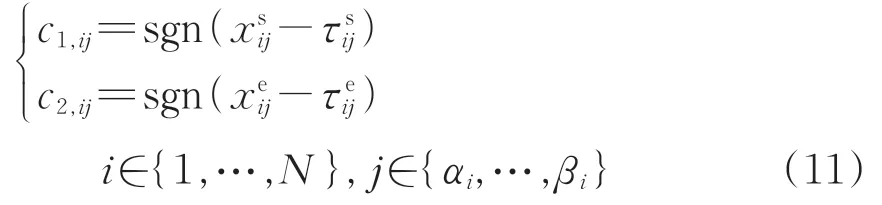
通過式（11）將式（2）中的參數替換，使后者轉換為式（12）所示的混合整數線性規劃模型。由此建立的列車運行調整雙目標優化模型P0為

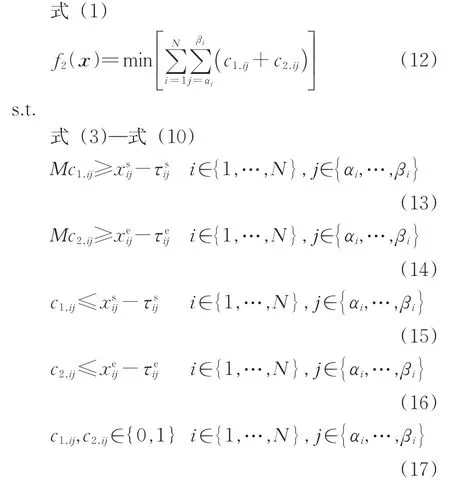
該模型屬于NP-hard問題［3］，無法在多項式時間內找到整個Pareto前沿，需要將其轉換為單目標優化模型（例如加權法或ε-約束法），通過商用求解器（如CPLEX，GUROBI 等）對一定規模下的問題在合理時間內得到Pareto前沿。

1.6 相關定義

參考文獻［18］，針對本文基于雙目標優化的高速鐵路列車運行調整問題，引入如下定義。

定義1（Pareto 支配）：目標向量u和v為2 個可行解集對應的優化目標，目標向量u支配v（記作u?v），當且僅當ub≤vb，?b∈{1，2，…，B}（B為目標個數），且u≠v。

定義2（Pareto 有效性）：對于可行解x，不存在其他可行解y，其目標函數值構成的目標向量f(x)和f(y)滿足Pareto支配關系f(y)?f(x)，則說明解x為Pareto有效性解，又稱為非支配解。

定義3（Pareto 解集，Pareto Set）：所有滿足Pareto 有效性的解的集合稱為Pareto 解集，又稱為非支配解集，記為APS。

定義4（Pareto 前沿，Pareto Front）：所有Pa?reto 最優目標向量的集合稱為Pareto 前沿，記為APF={f(x)|x∈APS}。

定義5（理想點，Ideal Point）：向量zIdeal=(zIdeal1，…，zIdealB)中每個元素都為每個目標函數fb(x)的最優解，可以通過zIdealb=minfb(x)求得理想點。

定義6（最差點，Nadir Point）：向量zNadir=(zNadir1，…，zNadirB)中的每個元素都為每個目標函數fb(x)在Pareto 前沿上的最大值。其中每個元素zNadirb定義為zNadirb=max {fb(x)|x∈APF}。

2 模型求解

求解多目標優化問題的方法包括ε-約束法和線性加權法，其原理都是通過將原問題轉換為多個不同的單目標優化問題，從而得到整個Pareto 前沿。其中，ε-約束法是通過將原有多個優化目標分為主目標和其他的次目標，并將其他的次目標作為約束進行單目標優化求解。相比于線性加權法，ε-約束法不需要設置權重，無需對目標函數進行歸一化處理，并能夠得到非凸前沿。

對模型P0，定義ε2∈[zIdeal2，zNadir2]為次目標優化上界，采用ε-約束法將目標函數f2(x)轉化為約束條件，則可將其轉化為模型P1，即

通過修改約束右邊的上限ε2，可以得到對應的Pareto前沿。

然而ε-約束法還存在以下3 個缺陷［19］：①在Pareto 前沿之外存在一些不必要的計算；②無法保證得到所有位于Pareto前沿上的解；③當優化目標超過2個時會顯著增加求解時間。因此，需要對ε-約束法進行改進。目前主流的改進方法如增廣ε-約束法（包括AUGMECON［19］和AUGMECON2［20］），雖然通過引入松弛變量、確定理想點和最差點等形式確定了約束范圍，但求解時增加了額外變量，從求解效率來看優勢不足。有必要進一步改進ε-約束法，在克服上述3個缺陷的基礎上實現高效求解。

分析式（2）可知，優化目標f2(x)均為整數情況，可利用理想點和最差點估計出Pareto前沿的最大個數。利用每次求解約束優化問題得到對應的次優化目標值f2(x?)，便能夠得到下一次優化的約束上界。相比于傳統ε-約束法固定約束增量下的求解，這種方法能夠減少不必要的重復非支配解的計算；相比于增廣ε-約束法，這種方法不僅可減少對輔助變量的使用，還能夠在無須為設置均勻分布的格點的基礎上保證求解到整個Pareto前沿。

采用改進ε-約束法求解模型P1的步驟如下。

步驟1：計算理想點，求解不含式（12）的優化模型P0，得到zIdeal1；求解不含式（1）的優化模型P0，得到zIdeal2。

步驟2：計算最差點，求解不含式（12）的優化模型P0，求解時增加額外約束f2(x)=zIdeal2，得到zNadir1；求解不含式（1）的優化模型P0，求解時增加額外約束f1(x)=zIdeal1，得到zNadir2。

步驟3：確定次優化目標取值范圍，設定約束為次優化目標最大值；根據理想點和最差點得到目標函數f2(x)的范圍為[zIdeal2，zNadir2]，求解最多（zNadir2-zIdeal2+1）個約束單目標模型P1 得到對應Pareto前沿，并令ε2=zNadir2，得到對應的模型P1。

步驟4：在設置的約束下計算調整方案，求解模型P1 得到當前最優解x?，記錄解[f1(x?)，f2(x?)]。

步驟5：更新約束值，令ε2=f2(x?)-1。

步驟6：判斷約束值是否為次優化目標最小值，如果ε2≠zIdeal2，則轉步驟4；如果ε2=zIdeal2，則繼續步驟7。

步驟7：輸出Pareto 前沿，將步驟4 中不同約束下求解模型P1 得到的解合并，去除其中的支配解，最終構成了模型P0對應的Pareto前沿。

此外，若決策者僅對部分Pareto 前沿感興趣，可以在目標函數f2(x)的范圍[zIdeal2，zNadir2]內選擇優化求解部分模型P1，得到部分感興趣的非支配解。

3 算例分析

選取京滬高鐵北京南—泰安區段為例，設置3 種干擾場景，采用本文模型和改進ε-約束求解算法進行列車運行優化調整；并與同樣采用本文模型但模型求解時分別采用加權法和先到先服務（First-Come-First-Served，FCFS）的啟發式策略（簡稱為FCFS 法）得到的結果進行比較，驗證本文模型和改進ε-約束法的合理性、有效性。

3.1 算例及參數說明

北京南—泰安區段共有7 個車站，自北京南開始依次編號為1，2，…，7。6 個區間的最小運行時間見表1。車站最小停站時間為2 min，相鄰列車最小追蹤間隔為4 min，M取值為1 000。下行開行列車40趟。

表1 區間最小運行時間tmin，run ik

根據不同的干擾情況（區間運行干擾、車站停車作業干擾），設置以下3個場景。

場景1：僅由車站停車作業干擾組成。設置列車2在北京南停車作業干擾時間為20 min，列車20在廊坊停車作業干擾時間為20 min，列車30 在北京南停車作業干擾時間20 min。

場景2：僅由區間運行干擾組成。設置列車4在北京南—廊坊區間運行干擾時間為15 min，列車18在廊坊—天津南區間運行干擾時間為20 min，列車32在北京南—廊坊區間運行干擾時間為20 min。

場景3：由上述2種干擾共同組成。設置列車3在北京南停車作業干擾時間20 min，列車25在廊坊停車作業干擾時間10 min，列車33在北京南停車作業干擾時間15 min；列車6 在北京南—廊坊區間運行干擾時間為15 min，列車15在廊坊—天津南區間運行干擾時間為20 min，列車28在北京南—廊坊區間運行干擾時間為20 min。

對于上述場景中未提及的列車及其途經區間和車站，均為正常場景，即其對應的區間運行干擾時間和車站停車作業干擾時間均為0。

3.2 多目標優化性能指標

為了驗證本文提出的改進ε-約束法的性能，采用了下面經典的多目標優化性能指標。

非支配解個數（Number of non-dominated so?lutions，NNS）：該性能指標描述了算法得到的近似Pareto前沿，NNS值越大說明該算法求解能力越強。

逆代距（Inverted generational distance，IGD）［21］：該指標綜合評價了非支配解集的收斂性和多樣性，IGD值越小，說明非支配解集A的質量越好。假設Ψ?為1個均勻分布在Pareto真實前沿的集合，Ψ為1個非支配解集，則Ψ的IGD值IIGD定義為

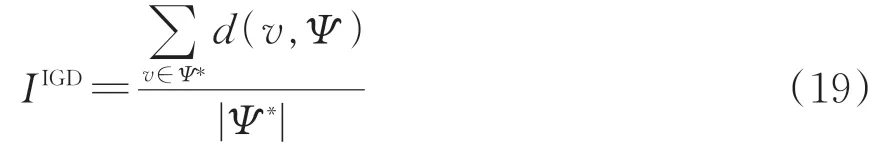
式中：v為解集Ψ?中的1 個解；d(v，Ψ)為v和Ψ中所有點的最短歐氏距離；|Ψ?|為集合Ψ?的勢。

超體積（Hypervolume，HV）［21］：該指標通過非支配解和參考點，計算出超體積。該性能指標同時評價了非支配解集的收斂性和多樣性。HV 的值越大，對應算法的性能越好。對于雙目標優化問題中的一個非支配解集A，其HV值IHV計算如下

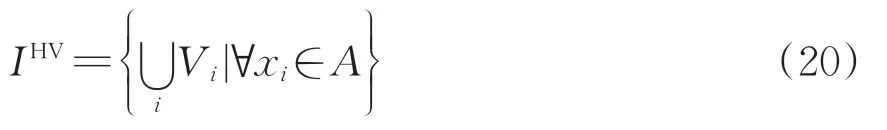
式中：xi為非支配解集A中的1個解；Vi為解xi對應的目標值f(xi)和參考點為邊界構成的矩形體積。

3.3 計算結果

針對3.1 節中給出的3 種干擾場景，在Intel Core i5-8265U CPU 1.60GHz，8GB 內存，操作系統Windows 10，64 位主機上分別采用改進ε-約束法、加權法和FCFS 法求解本文模型。其中改進ε-約束法和加權法均采用商用求解器GUROBI 9.1.0，通過YALMIP 工具包［22］在Matlab R2018b進行仿真求解。GUROBI 各參數采用默認值。加權法以w1f1(x)+(1-w1)f2(x)為優化目標，其中w1取范圍［0，1］之間的均勻間隔0.02 為權重，權重組合個數為51。

3.3.1 求解得到的Pareto前沿和解

3 種方法得到3 種場景下的Pareto 前沿和解如圖3所示。由圖3可以得到如下結論。

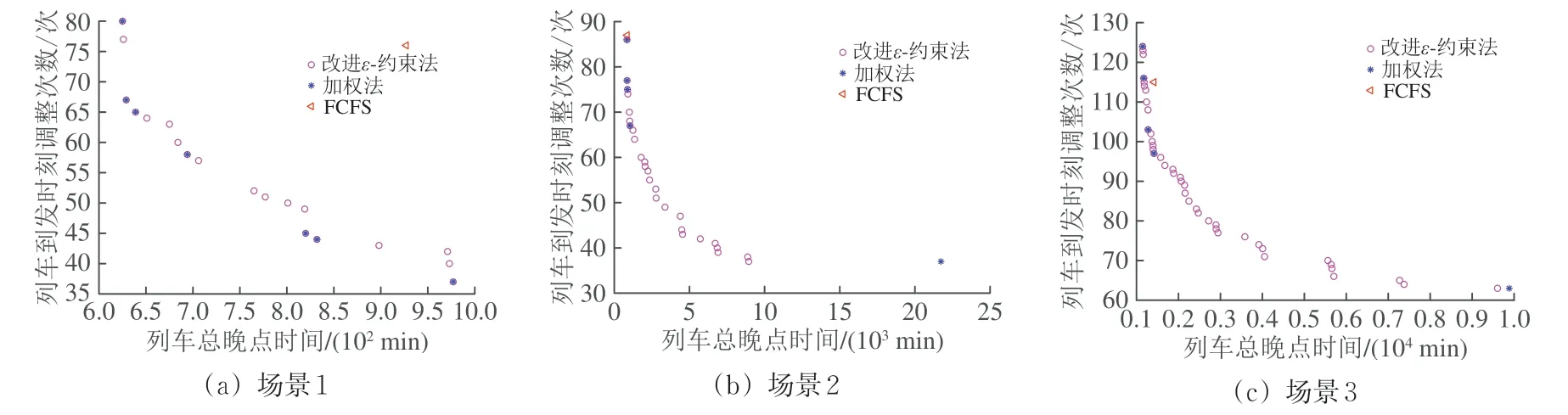
圖3 不同場景下的非支配解的分布

（1）采用改進ε-約束法求解，得到了3 種場景下的全部Pareto前沿。

（2）采用加權法求解，在場景1 中的前沿為Pareto 前沿的一部分（共7 個解），但無法得到對應的非凸前沿（共12 個解），即調整次數為77，64，63，60，57，52，51，50，49，43，42 和40的解。而在場景2 和場景3 中，僅得到了左上角的部分Pareto前沿，而右下角得到的是支配解。這些實驗結果說明處理多目標優化問題中，加權法存在一些缺點。分別為：無法得到非凸前沿；受不同優化目標函數值的范圍影響，需要對目標函數進行歸一化來避免加權后的單目標優化問題過于偏向優化某1 個目標函數，造成重復計算；加權法在邊界值時由于僅優化單個目標，沒有辦法保證另1個優化目標同時最小，會出現支配解。而本文提出的改進ε-約束法能夠克服這些缺點。

（3）采用FCFS 法求解，該策略以先到先服務的啟發式規則完成運行計劃調整，沒有專門對不同的優化目標進行處理，因此僅能得到1個解。對于場景1 中干擾類型均為車站停車作業干擾的情況，FCFS 法得到的解并不理想，與Pareto 前沿的差距較大。而對于場景2 和場景3 中含有區間運行干擾的情況，FCFS法相對效果有所提升。

3.3.2 調整后的列車運行圖

1）場景1

該場景下的列車計劃運行圖如圖4所示，不同車次的運行線通過粗細不同區分。運用改進ε-約束法（優化目標為（629，67））和FCFS 法（優化目標為（927，76））進行列車運行調整后，得到的運行圖分別如圖5和圖6所示，圖中紅色虛線表示運行調整后與原計劃運行圖不一致的列車運行線。由于加權法得到的結果大部分和改進ε-約束法相同，這里不做具體分析。由圖4—圖6可以看出：對于車站停車作業干擾的情況，改進ε-約束法會更多地通過調整受影響的列車次序完成調整，而FCFS 法依然按照干擾之后的列車次序調整到發時刻；針對第1 個優化目標，FCFS 法得到的結果是改進ε-約束法的1.47 倍，總晚點時間多298 min；在終點站時，改進ε-約束法下僅有1 趟列車存在晚點，其他受影響的列車在到達終點站之前均通過調整實現了恢復，而FCFS 法下還存在6 趟車到達終點站晚點情況。

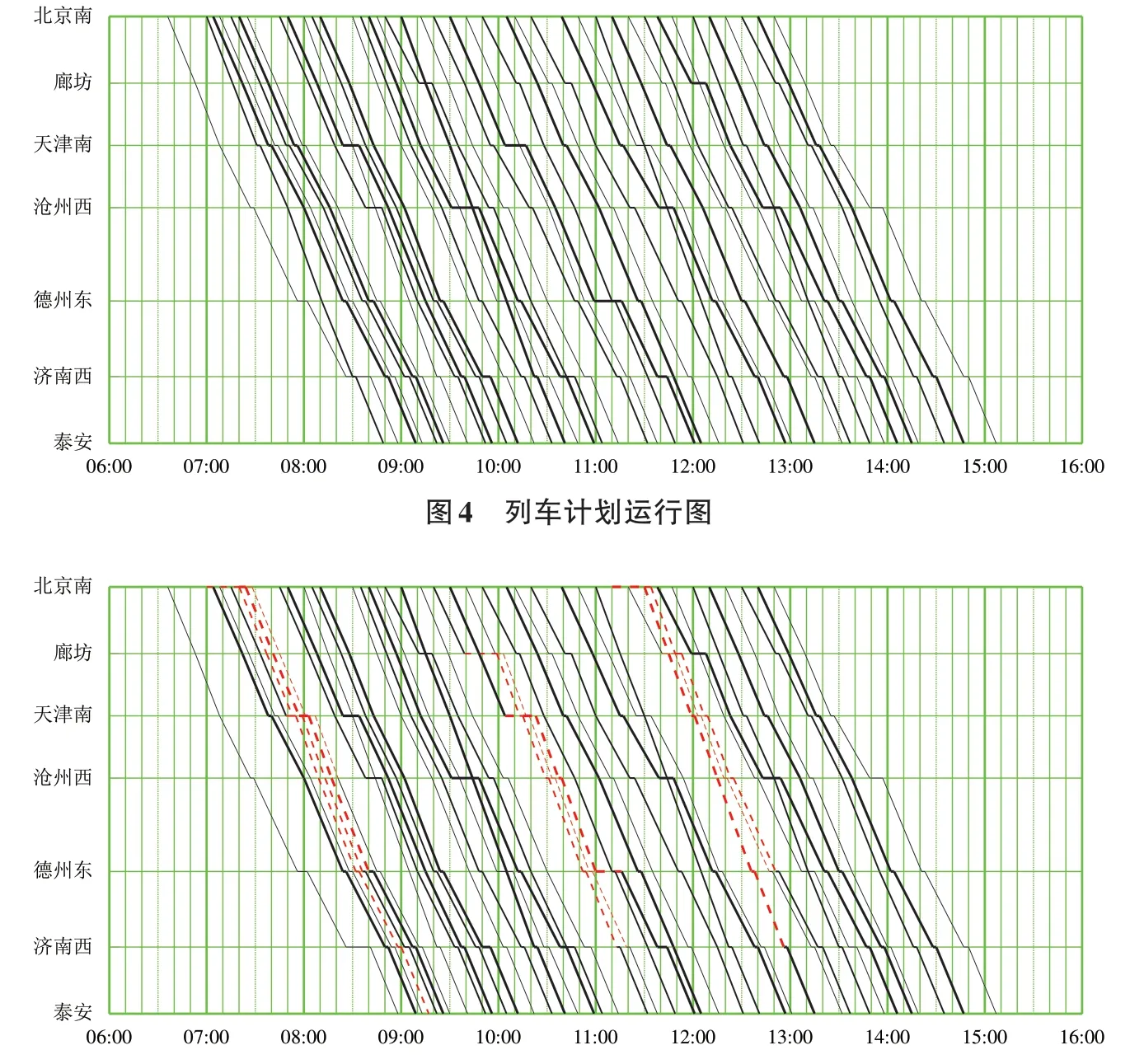
圖5 場景1下運用改進ε-約束法按優化目標（629，67）調整后的列車運行圖

圖6 場景1下運用FCFS法按優化目標（927，76）調整后的列車運行圖

2）場景2

該場景下，運用改進ε-約束法（優化目標為（843，86））和FCFS 法（優化目標為（857，87））進行列車運行調整后，得到的運行圖分別如圖7和圖8所示。由圖7和圖8可以看出：改進ε-約束法和FCFS 法對于場景2 前2 個干擾影響到的車次，均未調整發車次序，而是仍按原有次序依次調整到發時刻，僅在第3個干擾下分別對列車次序進行了調整，這是因為場景2 中的干擾均屬于區間運行干擾的緣故；對于第1 個優化目標列車總晚點時間，FCFS法得到的結果是改進ε-約束法的1.02倍，總晚點時間比后者多14 min；對于運行至終點站仍存在晚點的列車數量，改進ε-約束法下為2 列，而FCFS法為3列。

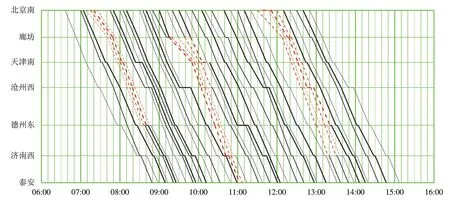
圖7 場景2下運用改進ε-約束法按優化目標（843，86）調整后的列車運行圖

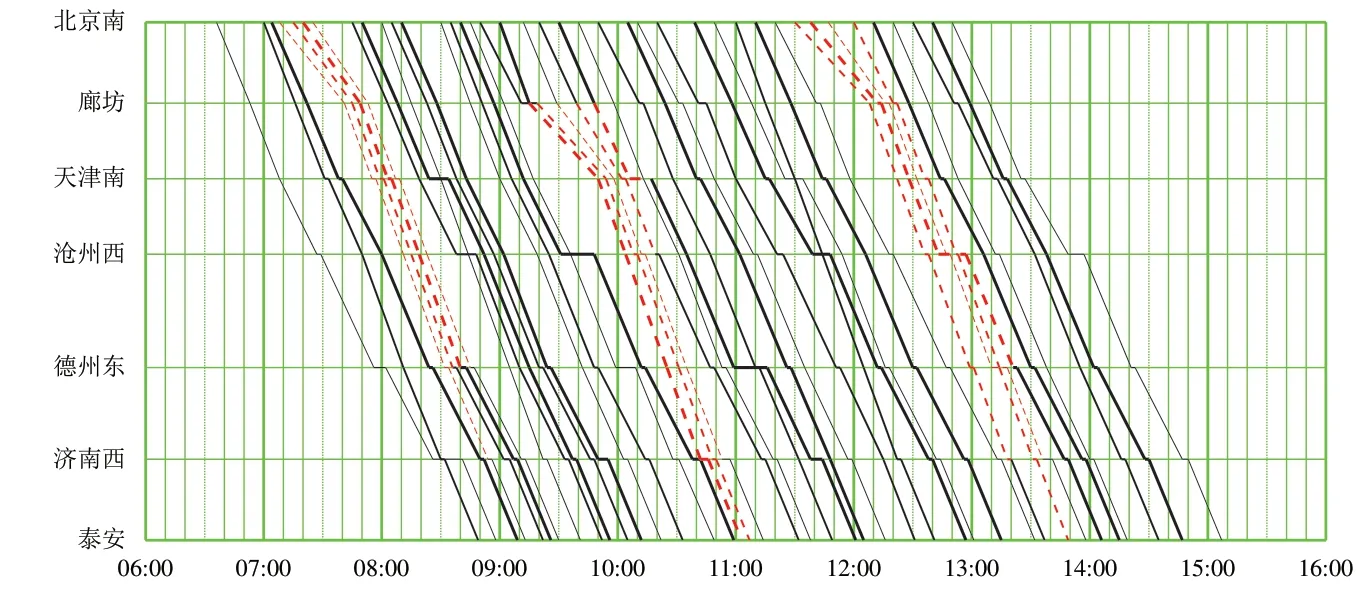
圖8 場景2下運用FCFS法按優化目標（857，87）調整后的列車運行圖

3）場景3

該場景下，運用改進ε-約束法（優化目標為（1 180，115））和FCFS 法（優化目標為（1 415，115））進行列車運行調整后，得到的運行圖分別入圖9和圖10所示。從圖9和圖10可以看出：在存在多種類型干擾的場景3 下，盡管對于區間運行干擾下FCFS 法和改進ε-約束法的調整方案相似，但由于FCFS 法沒有調整次序的能力，其無法得到全局最優解；在相同的第2 個優化目標下，對于第1 個優化目標列車總晚點時間，FCFS 法是改進ε-約束法的1.20 倍，總晚點時間比后者多235 min；對于運行至終點站仍存在晚點的列車數量，改進ε-約束法為4列，而FCFS法為7列。

圖9 場景3下運用改進ε-約束法按優化目標（1 180，115）調整后的列車運行圖

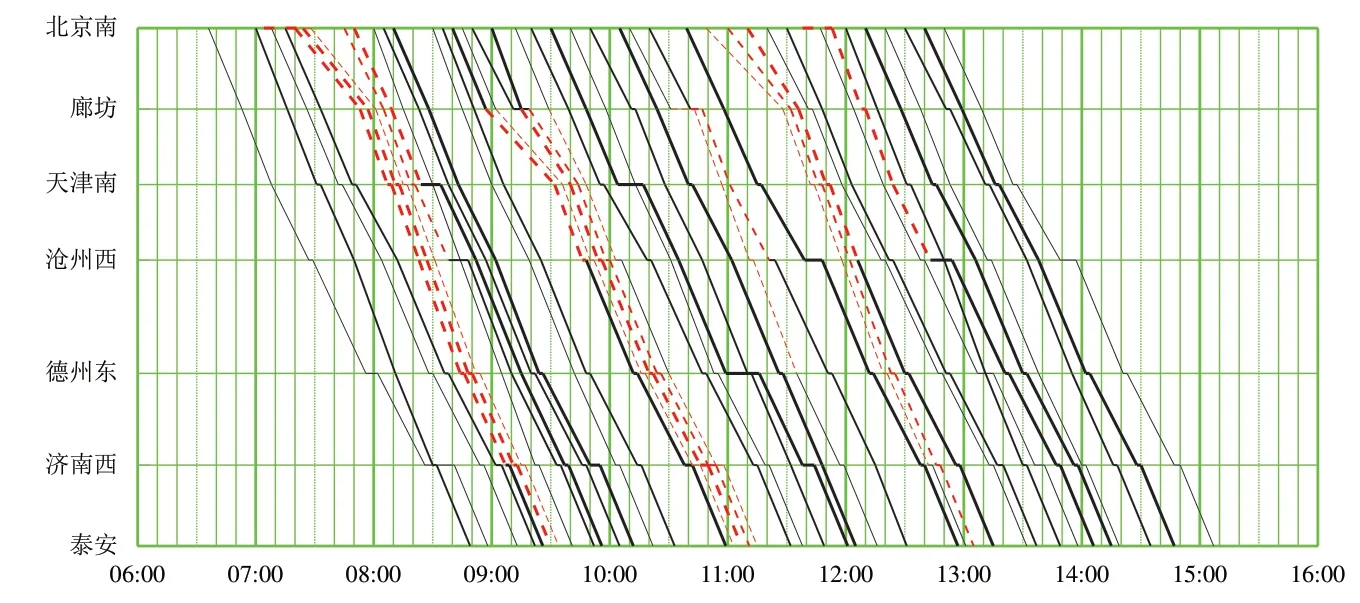
圖10 場景3下運用FCFS法按優化目標（1 415，115）調整后的列車運行圖

3.3.3 3種求解算法的性能指標比較

3 種場景下3 種求解算法的性能指標見表2。此外，表中還給出了算法的總計算時間和對應得到非支配解的平均計算時間，其中加粗數據表示該算法對應性能指標最優。從表2中可以看出：改進ε-約束法在NNS，IGD 和HV 這3 種性能指標中均優于加權法和FCFS 法，且得到了整個Pareto 前沿，但由于算出了所有的非支配解，所以其總計算時間較長，即在場景2 和場景3 中大于加權法和FCFS法；加權法并沒有算得全部Pareto前沿，還存在一些不必要的計算，在場景1中總時間最長；對于非支配解的平均計算時間，加權法同樣大于改進ε-約束法；FCFS 法作為一種啟發式策略，其計算時間會明顯優于其他基于求解器的精確算法，但其計算結果并不能保證最優。

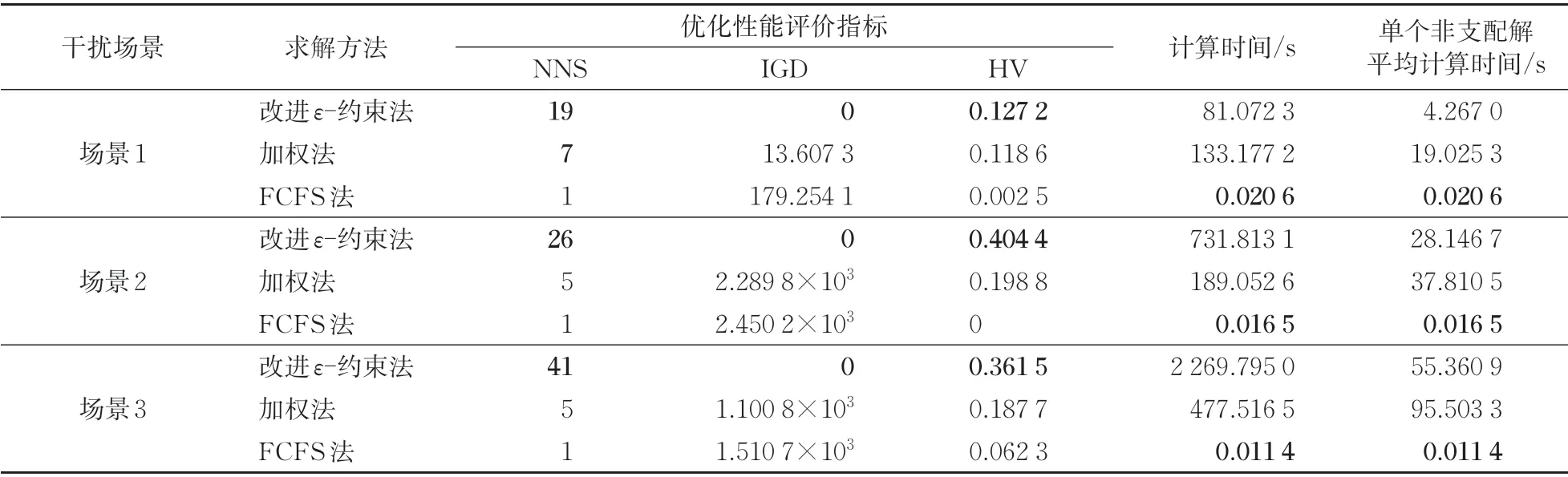
表2 不同場景下的算法性能

綜上，本文提出的改進ε-約束法，能夠有效求解提出的基于雙目標優化的高速鐵路列車運行調整模型的整個Pareto前沿。對于其計算時間在部分場景中較長的問題，實際中調度員可以有選擇的控制改進ε-約束法中的次優化目標對應的約束范圍，控制得到的非支配解的數量和偏好，降低調度員對不感興趣區域搜索所需要的時間。

4 結 論

（1）以列車運行調整的列車總晚點時間和列車到發時刻調整次數2 個優化目標，以車站作業、區間運行、追蹤間隔等時間為約束條件，構建高速鐵路列車運行調整的雙目標優化模型；對模型中的非線性項進行線性化處理；提出的改進ε-約束法對模型求解。

（2）提出的改進ε-約束法，得到了包括非凸前沿的整個Pareto前沿，可以為調度部門提供不同的列車調整決策方案，并且在非支配解個數NNS，逆代距IGD 和超體積HV 這3 個優化性能評價指標上均優于加權法和FCFS 法。與加權法相比，大部分非支配解對應列車總晚點時間和列車到發時刻調整次數相同，但改進ε-約束法的計算時間更短；對于邊界值，加權法可能會得到支配解，但改進ε-約束法對應調整后的總晚點時間更短。與FCFS法相比，改進ε-約束法能夠得到多樣化的結果，在列車到發時刻調整次數相近情況下，總晚點時間更短，終點站晚點列車個數更少。

（3）當更加復雜的干擾場景，求解問題規模增大后，計算整個Pareto前沿會消耗過多時間，可以在Pareto前沿中選擇調度員感興趣的搜索方向，搜索部分非支配解。此外，還可以通過設計一些啟發式方法和多目標進化計算算法，在有限時間獲得收斂性、多樣性好的近似前沿。