基于佳點集和萊維飛行原理的蜉蝣優化算法

吳霄，江海新，吳蕓，吳雪顏，江佳玉，童林

基于佳點集和萊維飛行原理的蜉蝣優化算法

吳霄，江海新，吳蕓，吳雪顏，江佳玉，童林

（九江學院 理學院，江西 九江 332005）

針對蜉蝣優化算法（Mayfly Algorithm，MA）在求解多峰函數時容易發生早熟收斂而陷入局部極值的缺陷，提出了一種基于佳點集和萊維飛行原理的蜉蝣優化算法（JLMA）．該算法首先采用佳點集初始化替代隨機初始化，以增強初始種群的遍歷性；然后修改了雄性蜉蝣的位置更新公式，消除了速度項對收斂速度的影響；最后，利用萊維飛行改變雄性蜉蝣位置的移動方向，防止算法陷入局部最優．在12個測試函數上的實驗結果表明，JLMA算法能跳出局部最優，提高解的精度，尋優效果更好．

蜉蝣優化算法；佳點集；萊維飛行

傳統優化算法一般要求優化問題是線性或可導的，然而，現實問題往往是非線性或不可導的．為了克服傳統優化算法的缺點，群智能優化算法應運而生，如粒子群算法（Particle Swarm Optimization，PSO）、遺傳算法（Genetic Algorithm，GA）、差分進化算法（Differential Evolution Algorithm，DE）等．

蜉蝣優化算法（Mayfly Algorithm，MA）是Konstantinos Zervoudakis[1]于2020年提出的新型群智能優化算法，它的靈感來源于蜉蝣的社會行為，特別是它們的交配過程．MA算法應用廣泛，已被用于線性天線陣列的模式合成優化[2]，集成風速預測系統[3]，與電解制氫系統相結合的光伏熱能收集器的性能預測[4]等不同領域．在求解某些優化問題時，MA算法存在收斂速度慢、易陷入局部最優等缺陷．針對這些缺陷，很多學者提出了不同的改進策略．Zhao J[5]等利用混沌數來代替MA算法中所涉及的隨機數，并對速度公式進行修正．陳偉超[6]等改變原算法在變異上的操作，將隨機選擇個體的隨機維度向全局最優個體的隨機維度靠近，并利用倒位操作，使最優個體的位置發生倒轉，提高了算法跳出局部最優的能力．王義[7]等引入自適應慣性權重衰減因子來平衡算法的探索和開發能力，并采用Lévy飛行和黃金正弦因子解決算法易陷入局部最優的缺點，增強了種群多樣性，提高了算法的收斂精度．雖然已有大量MA算法的改進研究，但因蜉蝣在移動過程中步長較短，導致算法收斂速度慢、易陷入局部最優等缺陷仍存在．為此，本文提出了基于佳點集和萊維飛行原理的蜉蝣優化算法（JLMA）．

1 蜉蝣優化算法

1.1　算法原理

1.2　雄性蜉蝣的運動

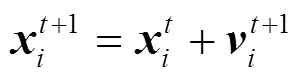
考慮到雄性蜉蝣在水面上表演交配舞且速度不能很大，因此，雄性蜉蝣的速度更新公式為

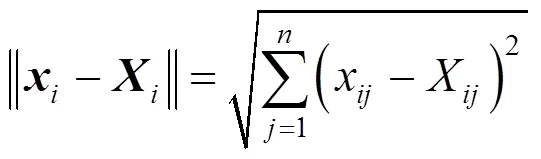
1.3　雌性蜉蝣的運動

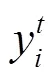
雌性蜉蝣速度的更新公式

1.4　蜉蝣的交配

雌雄交配是蜉蝣的生物特性，其交配過程是從雄性種群中選擇一個父本，從雌性種群中選擇一個母本，最好的雌性與最好的雄性繁殖，次好的雌性與次好的雄性繁殖，以此類推．具體交配公式為

隨后，交配得到的子代隨機進行變異操作，并分為雄雌種群．

2 基于佳點集和萊維飛行原理的蜉蝣優化算法

2.1　佳點集原理

圖1 初始種群在二維空間的分布

2.2　萊維飛行

萊維分布是法國數學家萊維（Lévy）于20世紀30年代提出的一種概率分布，事實上自然界中的許多隨機現象，如蒼蠅、鯊魚的飛行軌跡均符合萊維分布．萊維飛行[10-11]服從萊維分布，是一種短距離搜索與偶爾較長距離行走相間的移動方式．萊維飛行的位置更新公式為

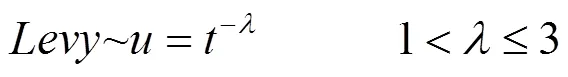
在實際應用中，萊維飛行常使用Mantegna算法模擬，相關數學表達式為

其中

2.3　JLMA算法步驟

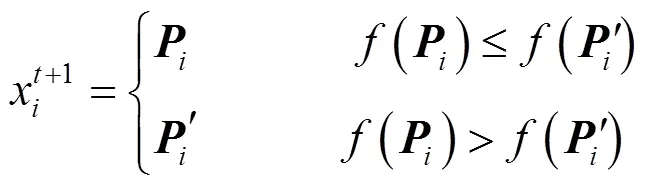
算法具體步驟：

Step 1 設置JLMA算法所需參數，利用佳點集原理初始化雌雄蜉蝣的位置，雌雄蜉蝣的初始速度設為零；

Step 2 計算蜉蝣個體的適應度值，找出當前的個體最優和全局最優；

Step 3 將萊維飛行加入雄性蜉蝣，根據式（13）～（15）更新雄性蜉蝣位置；

Step 4 根據式（4）（5）更新雌性蜉蝣的速度和位置；

Step 5 更新個體最優和全局最優；

Step 6 對雌雄蜉蝣進行排序，根據式（6）雌雄蜉蝣交配，產生子代，并對生成的子代進行變異操作；

Step 7 評估子代的適應度值，將子代分為雌雄，更新個體最優、全局最優和相關參數；

Step 8 判斷算法是否滿足最大迭代次數或精度要求，若滿足則算法停止搜索，輸出最優值；否則返回步驟Step 2繼續搜索．

2.4　算法復雜度分析

3 實驗仿真與分析

表1 基準測試函數

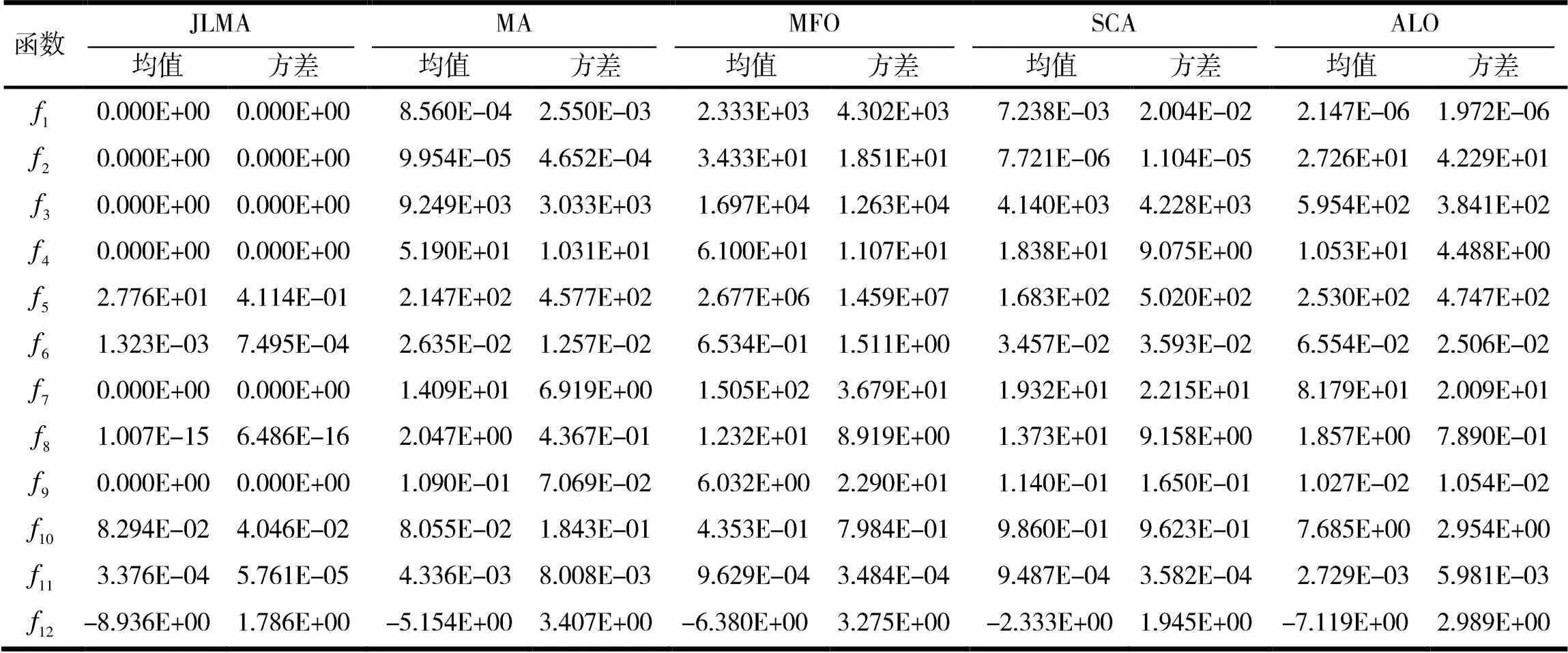
表2 不同算法在測試函數上的求解結果比較

為了更直觀地比較算法的性能，觀察不同算法之間收斂速度的差異，本文繪制了4個典型函數的收斂曲線（見圖2）．

圖2 不同函數的收斂曲線

由圖2可知，JLMA算法的收斂速度和求解精度均優于其他算法．由圖2a～b可看出，JLMA算法中的佳點集初始化，使得初始種群的質量得到提高，加快了算法早期的收斂速度；圖2c～d顯示，萊維飛行使算法有能力跳出局部最優，找到全局最優解．

4 結語

本文為改進MA算法易陷入早熟收斂的現象，基于佳點集和萊維飛行的數學性質，采用佳點集初始化種群位置，以提高初始種群的均勻性和遍歷性，同時修正雄性蜉蝣位置更新公式，引入具有跳躍性的萊維飛行，使算法具有跳出局部最優的能力．改進后的蜉蝣優化算法（JLMA）與4個對比算法在12個測試函數中的對比實驗證明了算法的優越性，并已被應用于焊接梁設計問題．

[1] Zervoudakis Konstantinos，Tsafarakis Stelios. A mayfly optimization algorithm[J]. Computers & Industrial Engineering，2020，145：106559．

[2] Xia Kewen，Wang Ting，Umar Abubakar．Pattern Synthesis of Uniform and Sparse Linear Antenna Array Using Mayfly Algorithm[J]. IEEE Access，2021，9：77954．

[3] Liu Zhenkun，Jing Ping，Wang Jianzhou，et al. Ensemble forecasting system for short-term wind speed forecasting based on optimal sub-model selection and multi-objective version of mayfly optimization algorithm[J]．Expert Systems with Applications， 2021，177：114974．

[4] Mohamed Abd Elaziz，Senthilraja S，Mohamed Zayed E，et al. A new random vector functional link integrated with mayfly optimization algorithm for performance prediction of solar photovoltaic thermal collector combined with electrolytic hydrogen production system[J]. Applied Thermal Engineering，2021，193：117055．

[5] Zhao Juan，Gao Zheng-Ming．The improved mayfly optimization algorithm with Chebyshev map[J]. Journal of Physics：Conference Series，2020，1684：012075．

[6] 陳偉超，符強．基于倒位變異的蜉蝣優化算法[J]．計算機系統應用，2021，30（8）：157-163．

[7] 王義，張達敏，張琳娜，等．基于黃金正弦與自適應融合的蜉蝣優化算法[J]．計算機應用研究，2021，38（10）：3072-3077．

[8] 王培崇，李麗榮，高文超，等．應用佳點集的混合反向學習人工魚群算法[J]．計算機應用研究，2015，32（7）：1992-1995．

[9] 陳毓隆．改進蝴蝶算法及其在多模態優化和SVM優化的應用[D]．南寧：廣西大學，2019．

[10] 王慶喜，郭曉波．基于萊維飛行的粒子群優化算法[J]．計算機應用研究，2016，33（9）：2588-2591．

[11] 李榮雨，王穎．基于萊維飛行的改進粒子群算法[J]．系統仿真學報，2017，29（8）：1685-1691，1701．

[12] Mirjalili Seyedali．Moth-flame optimization algorithm：A novel nature-inspired heuristic paradigm[J]．Knowledge-Based Systems，2015，89：228-249．

[13] Mirjalili Seyedali．SCA：A Sine Cosine Algorithm for solving optimization problems[J]．Knowledge-Based Systems，2016，96：120-133．

[14] Mirjalili Seyedali．The Ant Lion Optimizer[J]．Advances in Engineering Software，2015，83：80-98．

mayfly optimization algorithm based on good-point set and Lévy flight principle

WU Xiao，JIANG Haixin，WU Yun，WU Xueyan，JIANG Jiayu，TONG Lin

（School of Science，Jiujiang University，Jiujiang 332005，China）

To address the shortcoming that the mayfly algorithm（MA）is prone to premature convergence and falling into local stagnation when solving multimodal functions，proposed a mayfly algorithm based on good-point and Lévy flight（JLMA）．The algorithm first adopts good-point set initialization instead of random initialization to increase the traversal of the initial population．Then modifies the position update formula of male mayflies to eliminate the influence of the velocity term on the convergence speed．And finally uses Lévy flight to change the moving direction of male mayfly positions to prevent the algorithm from falling into local optimum．Our experiments on 12 test functions show that the JLMA algorithm can jump out of the local optimum，improve the accuracy of the solution，and have a better result in finding the optimum.

mayfly algorithm；good-point set；Lévy flight

1007-9831（2022）03-0036-07

TP18

A

10.3969/j.issn.1007-9831.2022.03.008

2021-12-16

江西省教育廳科技項目（GJJ201814，GJJ211823，GJJ211825）；江西省2021年大學生創新創業訓練計劃項目（s202111843031，s202111843039）；九江學院2021年大學生創新創業訓練計劃項目（x202111843141，x202111843144，x202111843150）

吳霄（2001-），男，江西贛州人，在讀本科生．E-mail：2302437854@qq.com

江海新（1980-），男，山東泰安人，講師，從事智能優化算法研究．E-mail：jianghaixn@163.com