大概念視角下的六年級總復習的整體復習
——以“用分數、百分數和比的知識解決問題”為例

浙江杭州市蕭山區紅墾學校（310000） 俞建華

一、課題的現實背景

隨著課程改革的不斷推進，“知識整體教學”已經成為教育領域的熱點詞匯。小學六年級第二學期的數學總復習課總是讓教師愁、學生怨。因為總復習課經常是簡單的知識整理課與高強度的習題訓練課，既沒有知識的整體梳理，更沒有思維的發展、方法的遷移。

因此，筆者以大概念視角下的知識整體復習為研究主題開展研究。

二、課題的研究意義

1.促進學生建構大概念。通過研究完善教學設計及教學應用，有助于師生加強對數學學科大概念的提煉與理解。

2.提高復習課課堂效能。將大概念教學與學生自主學習相結合，有利于活躍課堂氣氛，提高復習課課堂效能。

三、大概念的操作定義

大概念（Big Ideas/ Big Concepts），亦被譯為大觀念。在教育領域，有關大概念的研究可追溯到杰羅姆·布魯納（1982）對教育過程的研究。布魯納強調，無論教師教授哪類學科，一定要使學生理解該學科的基本結構，這樣有助于學生解決課堂內外所遇到的各類問題。學習這種基本結構就是學習事物之間是怎樣相互關聯起來的。掌握學科的基本概念架構，有助于記憶和保留學科知識，并促進學習的遷移。

比如，兩個量的比較，常見方法之一就是比較兩者的比率關系（倍比問題）。比率這一概念在數學學習中有重要的作用，是學生學習比例、一元函數的基礎。實際上，倍、分數（表示率）、百分數、比等概念的本質都是比率。可見，理解兩個量的比率是學生認知結構建立的重點。

學生認知結構中的數學概念體系是按“整數—分數—比例”的順序依次建構的。在小學階段，一般當比率大于1 時，習慣說比較量是標準量的幾倍（用整數或小數表示）；當比率小于1 時，習慣說比較量是標準量的幾分之幾。而百分數在表示比率時則結合了以上兩種情況，百分號上的數可以小于100，也可以大于或等于100。因此，在教學比的時候，可要求學生靈活使用整數、分數、小數等形式來表示比值。

筆者在梳理教材的過程中發現，“比率”這一大概念在小學階段是按下面的結構編排的：

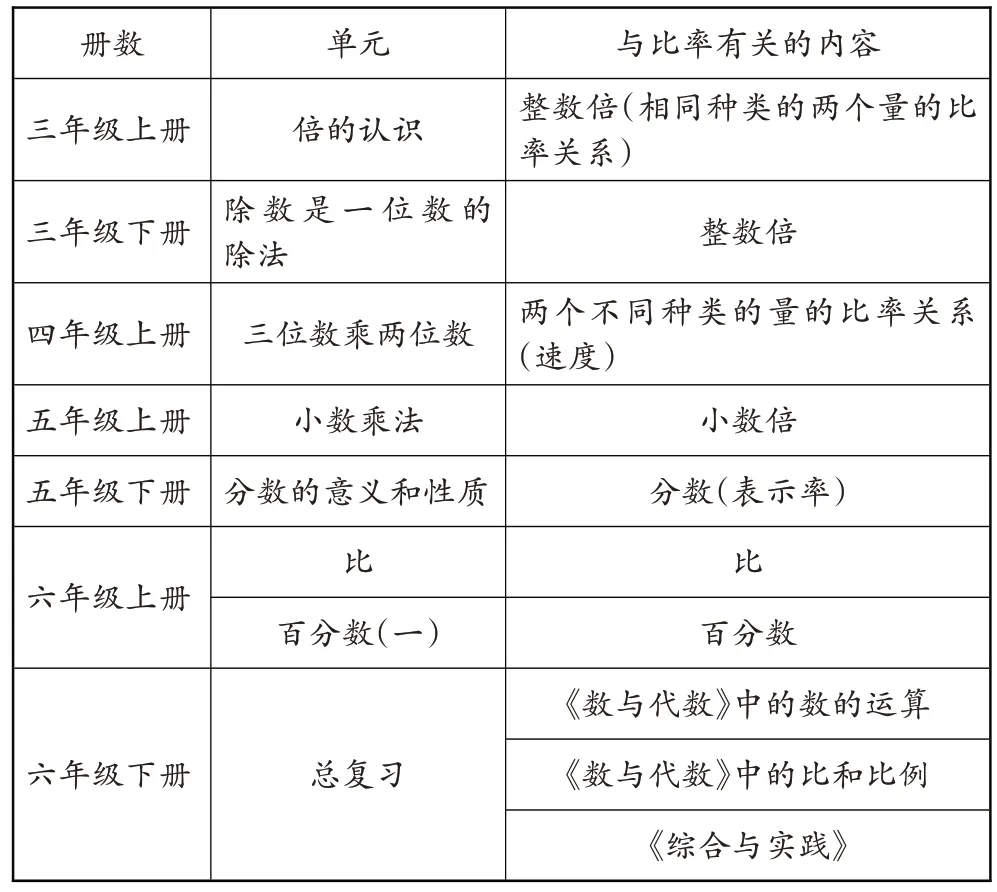
冊數三年級上冊三年級下冊四年級上冊五年級上冊五年級下冊六年級上冊單元倍的認識除數是一位數的除法三位數乘兩位數小數乘法分數的意義和性質比百分數（一）六年級下冊總復習與比率有關的內容整數倍（相同種類的兩個量的比率關系）整數倍兩個不同種類的量的比率關系（速度）小數倍分數（表示率）比百分數《數與代數》中的數的運算《數與代數》中的比和比例《綜合與實踐》

可以看出，整數倍的學習是學生第一次接觸比率，小數倍、分數（表示率）、百分數、比的內容都是對整數倍的擴展，這些知識的大概念就是比率。

四、整體復習的策略

點分數、百分數和比的知識，都是比率的拓展知識，三個知識點有相融相通之處，但教材安排總復習時又讓它們“各自為政”，這樣很難讓學生對知識有整體的理解與建構。于是筆者擯棄按教材逐一教學的常規方法，將三個知識點一并拋出，以基本問題為主干，以學生自主學習為旁枝，使新舊知識得以連接和鞏固，使學生的創造性思維得以發展。下面以“用分數、百分數和比的知識解決問題”為例談談相關教學策略。

1.明確“大同小異”，培養一種宏觀視野

教學的主體是學生，教師以“比率”這一大概念為核心，給學生創設一種良好的、和諧的提出和探討問題的氛圍，鼓勵學生對所學的知識大膽質疑，主動梳理知識，明確以“比率”為核心的知識鏈。

［案例1］明確“大同小異”

出示預學作業：

（3）一件襯衣原價125 元，現在降價20%。現在售價是多少元？

（4）一件襯衣降價20%后，售價為100 元，這件襯衣的原價是多少元？

（5）一件襯衣的售價為100 元，一條長褲的售價是這件襯衣的150%。這條長褲的售價是多少元？

（6）一件襯衣的售價為100 元，一條長褲的售價和這件襯衣的售價之比是3∶2。這條長褲的售價是多少元？

師：這是昨天的預學作業，請以四人為小組先相互說一說，這六道題目中的哪幾道題目之間有聯系？

教師的基本問題：哪幾道題目之間有聯系？

生1：第1題和第2題有聯系，都是分數問題，關鍵句相同，單位“1”都是原價。

生2：它們的相等關系都是“原價×=售價”。

生3：它們的區別是什么？

生4：區別是第1 題的單位“1”已知，用乘法；第2題的單位“1”未知，用方程或者用除法。

生5：還有類似的題目嗎？

生6：第3題和第4題都是百分數問題，有聯系。

……

生7：第1 題和第3 題有聯系，只不過把分率轉化成了百分率，其他都一樣。

生8：請問解題思路一樣嗎？

生9：解題思路與解題策略基本一樣，大同小異，可以用線段圖說明。

生10：通過畫圖可以發現，第 1 題和第 3 題，以及第2 題和第4 題只是分率和百分率的不同表述。第1題和第2題，以及第3題和第4題只是條件和問題互換。

生11：第5 題和第6 題的第一個信息和問題都一樣，區別是第二個信息用兩種不同的關系進行表述。

生12：其實說的都是“襯衣的售價是單位‘1’，長褲的售價是襯衣的1.5倍”。

生13：我發現這些題目都是研究兩個量之間的倍數關系。

生14：第5 題和第6 題也可以用線段圖來說明，它們也是大同小異。

生15：我發現分數問題和百分數問題、比的問題都是相通的，都是以前“整數倍”知識的擴展。那解決這些問題的關鍵是什么？

生17：列出相等關系。

生18：不管是找單位“1”，還是列出相等關系，都是從關鍵句入手。

［反思：通過教師的基本問題“哪幾道題目之間有聯系？”，以及學生之間的自主提問“它們的區別是什么？”“還有類似的題目嗎？”“請問解題思路一樣嗎？”“那解決這些問題的關鍵是什么？”等，學生將零散的、個別的知識系統化和條理化，這是形成概念體系的重要過程。

全面分析、縱橫比較是高階思維的體現，也是學生學習數學的一種重要方法。而總復習課是學生學會梳理知識、分析問題、構建知識網絡的契機，有利于培養學生的宏觀視野，例如有學生提出“我發現這些題目都是研究兩個量之間的倍數關系”。

為此，教師應不斷強化學生梳理、分析的意識，讓學生認識到知識之間有聯系。在學生分析完成后，教師可補充一個基本問題“剛才的分析，哪些是你想到的？哪些你沒有想到？”，以此來提高學生自主學習的能力。］

2.學會“無中生有”，發展一種整體思維

愛提問題的人，往往是積極思考、富有創造力的人。因此，教師要隨時注意挖掘教材中隱藏的“發現”因素，創設使學生主動發現問題、提出問題的情境，啟發學生自己發現問題，自主地去嘗試、探究、感悟，從而體會到知識的本質——大概念。

教師適時地制造“無中生有”的問題，能刺激學生大腦皮層的興奮中心；能使教學過程跌宕起伏、張弛有度；能使教學潛移默化，收到潤物細無聲的效果。

在種植玉米之前，我們需要做土地整理，主要是去除去年在土地上種植的農作物的根部，或者完全粉碎[1]，以避免影響玉米的正常種植或影響其產量。事實上，粉碎去年作物的根部更有利于作物栽培，因為粉碎的材料可以用作肥料來提高土壤肥力。然而，由于玉米高產的需要，土壤肥力仍然不足。因此，還需要在播種前施用基肥，才能有效地保證玉米的產量和收入。

［案例2］學會“無中生有”

師：在解決問題時，找到關鍵句、分析關鍵句、正確理解關鍵句是十分重要的。

出示題目：

信息：學校603班有男生16人、女生20人。

要求：根據信息，聯想關鍵句，并寫出算式。

師：這是我們班男生和女生的信息，你能根據這兩個信息想到哪些關鍵句，或者提出哪些問題？請在1分鐘內寫出不同的算式表示問題。

教師的基本問題：想到哪些關鍵句？

學生匯報情況1：男生人數是女生人數的幾分之幾或百分之幾？或兩者相比是幾比幾？

算式：16÷20或16÷20×100%或16∶20

學生匯報情況2：女生人數是男生人數的幾分之幾或百分之幾？或兩者相比是幾比幾？

算式：20÷16或20÷16×100%或20∶16

學生匯報情況3：男生人數比女生人數少幾分之幾或百分之幾？

算式：（20-16）÷20或（20-16）÷20×100%

學生匯報情況4：女生人數比男生人數多幾分之幾或百分之幾？

算式：（20-16）÷16或（20-16）÷16×100%

生1：我發現這里除了男生人數和女生人數，還有一個量。

學生匯報情況5：男生人數是全班人數的幾分之幾或百分之幾？或兩者相比是幾比幾？

算式：16÷（16+20）或16÷（16+20）×100%或16∶（16+20）

學生匯報情況6：女生人數是全班人數的幾分之幾或百分之幾？或兩者相比是幾比幾？

算式：20÷（16+20）或20÷（16+20）×100%或20∶（16+20）。

生2：我發現所有的表述其實都是比較量與標準量。

……

［反思：看到兩個信息后，學生“無中生有”地提出了許多問題（關鍵是這些問題都圍繞“比率”這一大概念展開），并根據已知信息解決了這些問題，這就是學生創新思維得到發展的最好體現。

從教師提出基本問題“想到哪些關鍵句？”，到學生自主想到“我發現這里除了男生人數和女生人數，還有一個量”“我發現所有的表述其實都是比較量與標準量”這一過程中，學生的全面分析、客觀評價、合情創新此起彼伏，充分發揮了“無中生有”的作用，全面打開了學生的思維通道。學生通過自主思考、小組交流、組際匯報，充分拓寬了思維廣度，提升了思維深度。

問題的發現，不僅使課堂上處處閃爍探究、創新的火光，更使學生進入深層次的學習探索階段。學生在自讀、自問、自悟、自解的過程中初步體驗到嘗試性探究學習的成功喜悅，從而完成“要我學”向“我要學”的過渡。特別是活動中教師對學生解答的理性評價，能讓讓學生經歷“數學化”與“再創造”的思維過程，有助于學生實現高階思維的升華。］

3.理解“觸類旁通”，引導一種建構啟示

部分學生在多年的學習生涯中都是被“抱大”的，已經習慣了“你講我聽”的模式，習慣了“被動學習”，他們不敢也不善于發現問題，不敢相信自己是“學習的主人”，明顯缺乏獨創性。

為此教師應通過各種形式培養學生自主學習的信心，這是學生自主學習取得成功的關鍵一步。鼓勵、啟發和引導學生通過不同的途徑，從不同的角度，用不同的方法解決問題，不僅活躍了學生的思維，開闊了學生的思路，同時也促進學生養成善于求異的習慣，從而培養學生的創新能力和自主學習的信心。

觸類旁通是學生數學學習的一種能力。學生如果掌握了這種能力，學習起來就能得心應手。然而在學習中，經常是學生已經“觸類”了，但不能“旁通”，如此就會出現“啟而不發”的現象。教師在復習課中要把知識放到全部教材體系之中，能承上啟下，這樣學生就會慢慢養成觸類旁通的本領，建構大概念的框架。

［案例3］理解“觸類旁通”

師：在不改變解題方法的基礎上，如何增加題目的難度？

教師的基本問題：如何增加題目的難度？

生1：把關鍵句表述得更加復雜一些。

生2：讓分數、百分數和比的知識混在一起。

生3：學校603班有36人，男生與女生的人數比是4∶5，其中75%的男生喜歡上數學課，喜歡上數學課的男生有多少人？

生4：“男生是全部人數的”還可以表述為“男生與女生的人數比是4∶5”“男生是女生人數的”“男生是女生人數的80%”等，這些知識都是相通的。

生5：解答時，要把信息化繁為簡，那編題時就要化簡為繁。

生6：學校603 班有36 人，男生比女生人數少20%，其中喜歡數學課的男生人數是不喜歡數學課的男生人數的3 倍，喜歡上數學課的男生有多少人？

生7：原來“其中75%的男生喜歡上數學課”這個信息還可以轉換成倍數關系來表述。

……

［反思：“觸類旁通”是一種思維習慣或一種意識，教師要讓學生在不斷地舉一反三的過程中逐步形成。另外，要讓學生明白“化繁為簡”和“化簡為繁”其實是相通的，是同一思路的兩種不同路徑。

學生在梳理分數、百分數、比的知識時，又回歸到整數倍的知識，說明學生對“兩個量之間的關系（比率）”已基本融會貫通，“比率”這一大概念在學生大腦中已根深蒂固。

當然，要學生達到“觸類旁通”，除了對所做的題目有充分的分析和總結，更主要的還是教師要通過思考角度的變化、思考方法的改變、題型設計的變化等來創造多樣化的思維環境，接通多方位的解題思路，用“教”的創新火種點燃“學”的創新火種，從而提高學生思維的變通性和廣闊度，引導學生根據自己的實際情況進行大膽的自我創新。］

五、實踐感悟

大概念視角下六年級總復習的整體復習是授人以魚，更是授人以漁。這體現了現代教育的目標和方向。正如張奠宙教授所說：“數學教學需要從整體上把握。要恢復學生火熱的思考，就要幫助學生揭示數學的內在聯系。”這其實就是要促進學生數學高階思維能力的形成與發展。

實踐中發現，在大概念視角下整體復習的教學中，教師提出基本問題是必不可少的，這也對應了在杰伊·麥克泰格和格蘭特·威金斯理解為先的教學設計模板中，大概念和基本問題都是配套出現的情況，因為他們把基本問題比喻成理解大概念的“鑰匙”，通過基本問題可以引導學生自主提問，探尋大概念。這就需要教師做好以下三點：

1.理解基本問題

基本問題與非基本問題的根本區別在于目標不同，基本問題是和大概念目標配套的，指向專家思維方式，而非基本問題則和知識與技能目標配套，指向記憶已有專家結論。用杰基·阿克里·沃爾什的話來說，就是基本問題是“為討論”，而非基本問題則是“為背誦”。

2.設計基本問題

基本問題是與大概念配套的，因此教師確定基本問題大體上是循著大概念的方向尋找的。確定了基本問題后，還要經過一個精心加工的過程，主要是從學生的角度考慮三個方面：是否能激發學生的興趣？是否能激活學生的生活體驗？是否適合學生的發展水平？

基本問題引發的是一個不斷討論的過程，可以是以教師為中心的師生討論，也可以是無中心的師生討論，這時教師才真正是小威廉姆·多爾提到的“平等者中的首席”。

3.把握基本問題

基本問題常常呈現為問題鏈，以各種形式貫穿于課堂的始終。在教學中，基本問題根據承擔的不同功能，可分為導入式問題、展開式問題和總結式問題。其中，導入式問題的功能主要是吸引學生投入學習中，因此，要帶有一定的趣味性。展開式問題則不斷推動學生具體與抽象之間的協同思維，挑戰學生原有的觀點，使之更正確、嚴密，有時會帶有一些“挑釁性”，以激發學生的深入思考。展開式問題很多是以追問的方式出現，體現支架思維，不斷推進學生的思考。總結式問題主要是在一個討論階段結束時，提供適時的回顧，既可以是總結和梳理，也可以是展望和提問。值得一提的是，這三類問題并非按時間順序排列，在大概念視角下的整體復習中，這三類問題根據需要交替出現在教學中。