基于時空卷積神經網絡的數據缺失交通流預測

張壯壯，屈立成，李 翔，張明皓，李昭璐

長安大學 信息工程學院，西安 710064

作為智能交通系統的基礎，交通流預測在路徑規劃和出行誘導等方面正在發揮著越來越重要的作用[1]。有效的交通流預測不僅可以為交通管理部門提供有力的決策支持，還可以為出行者提供及時的路況信息，從而避免交通擁堵，節約出行時間[2]。

為了對交通運行狀態進行更加準確地感知，各種類型的交通檢測裝置正在被廣泛地安裝與使用，越來越多的交通狀態數據被統一收集和儲存，極大地推動了以深度學習為代表的數據驅動型交通流預測算法的蓬勃發展[3]。如劉明宇等人[4]使用基于門控循環單元（gated recurrent unit，GRU）的遞歸神經網絡，利用交叉驗證法進行了交通流預測。戢曉峰等人[5]利用深度學習理論建立了LSTM-SVR預測模型實現交通流預測。Li等人[6]將交通流建模表示為有向圖上的擴散過程，并且引入擴散卷積循環神經網絡（DCRNN）進行交通預測。劉釗等人[7]提出了一種混合預測模型（KNN-SVR），利用K近鄰方法的搜索機制，重建與當前交通狀態近似的歷史交通流時間序列，結合支持向量回歸模型的特征實現短時交通流預測。這些預測模型使用大量歷史數據進行訓練，挖掘交通流數據之間的隱含關系并實現交通流狀態預測功能，但是在實際使用時均需要保障用于預測的數據序列的正確性和完整性，所以也就無法應對數據缺失情況下的預測場景。

由于數據缺失會對預測結果產生巨大的影響，現實中的交通檢測裝置卻常常會因為供電、通信等原因不可避免地產生數據缺失或傳輸錯誤，從而導致預測模型的精度下降甚至失效，因此保障預測數據的完整性和連續性就顯得非常重要。交通數據中的缺失值可以通過數據插補方法來進行處理[8]，如平均值法、張量法等。平均值法是將某個變量的缺失值替換為該變量的對所有觀測值的平均值[9]，該方法隱式地假設變量間彼此獨立并且服從正態分布，而不考慮屬性之間的內在關聯結構。張量法通過引入張量模式對交通數據進行建模[10]，采用一種高效的張量方法完成高精度張量補全，并推導缺失的序列數據。很多學者使用這些方法進行帶有缺失值的交通流預測。如Chen等人[11]將貝葉斯矩陣分解模型擴展到一個高階案例，用于了解時空交通數據中的基礎統計模式-貝葉斯高斯CANDECOMP/PARAFAC（BGCP）張量分解模型。何領朝等人[12]提出了一種基于自適應秩動態張量分析的算法來進行短時交通流預測。Cui等人[13]提出了一種用于時空數據預測的圖馬爾可夫網絡（GMN）來同時處理缺失值和預測交通狀態。Whitlock等人[14]開發馬爾可夫鏈蒙特卡羅（Markov chain Monte Carlo）方法用于提供缺失序列的預測，進而用于生成其他序列中的一些預測。這類方法通常需要覆蓋很長一段時間的大型數據集才能獲得良好的插補性能，但是這類大型數據集并不總是可用，大多數的交通預測模型都要求在預測之前先對歷史數據進行插補操作以提高預測的精確程度，但當前的插補方法多集中于解決少量隨機發生的數據缺失，無法應對數據長時間連續缺失的狀況。根據連續數據缺失的補全進行交通流預測仍然是一個熱點研究領域。

考慮到路網中檢測器之間的時空關系和交通流的連續特性，以及交通流狀態數據的周期性和隨機性特征，本文提出了一種利用時空卷積神經網絡（spatialtemporal convolutional neural network，ST-CNN）進行多種數據缺失情況下的路網交通流預測方法。通過構建路網時空矩陣，體現觀測點橫向分布的時間相關性和縱向分布的空間相關性，并通過掩碼矩陣來標記交通狀態數據的缺失情況，利用卷積神經網絡提取整個路網交通狀態的分布特征和依賴關系，實現在數據連續缺失情況下的交通流預測，這對于交通流時間預測的發展有很大優勢。

1 時空卷積神經網絡模型

時空卷積神經網絡模型框架如圖1所示。為了能夠使預測結果更有效，本文使用時空卷積神經網絡模型，首先輸入歷史數據，根據時空矩陣和掩碼矩陣來標記路網數據的缺失情況，然后使用時空卷積神經網絡模型進行模型訓練，提取交通流特征，最后根據其交通流特征進行交通流預測。

圖1 時空卷積神經網絡模型框架Fig.1 Framework of spatial-temporal convolutional neural network model

1.1 時空序列矩陣

時空序列矩陣主要從時間和空間兩個維度進行構建[15]。時間主要是前后順序的記錄，空間主要是檢測器位置的記錄，根據檢測器在特定時間記錄的有關車輛速度和位置的特定信息，估算每個路段的時空交通信息，并將其進一步集成到時空矩陣中，成為時空圖像。

在時間維度上，時間通常從一天的某個時間點開始到第二天的時間點開始，進而確保時間的完整性，并通過給定的時間間隔Δt收集交通流數據，例如，5 min、15 min和60 min，具體取決于檢測器設備的采樣分辨率。為了獲得更有效的交通數據并使交通預測更加有效，可以對這些數據進行匯聚來選取更合適的時間間隔，例如10 min、15 min等。

在空間維度上，所選的上下游檢測器位置被視為具有內部狀態的點序列，包括交通狀態、平均速度等。由于點序列中的許多區域都是穩定的，并且缺乏多樣性，數據密集或不足都將影響交通流量預測的準確性。因此，為了使縱軸有意義，將點分為多個部分，每個部分代表相似的交通狀態。根據檢測器在道路上的位置，對檢測器進行空間分類，將其裝入縱軸，同時，為該段選擇合適的時間，將其裝入橫軸，然后用矩陣表示狀態，最后生成圖像。圖2中顯示了路網中的檢測器、交通狀態數據、時空矩陣和最終生成的圖像之間的關系。

圖2 交通狀態時空矩陣的構建與可視化Fig.2 Construction and visualization of spatial-temporal matrix of traffic state

最后，可以根據時空維度信息構建時空矩陣。在數學上，通過以下方式表示時空矩陣x t：

式中，是第n個檢測器在t時刻的交通狀態，n是檢測器的數量，n∈?*，t是時間點，L為時間序列的長度。

1.2 缺失掩碼矩陣

掩碼是指用一串二進制數字，通過與目標字段進行位與運算，達到屏蔽指定位的目的，掩碼矩陣不僅可以模擬數據的缺失，還可以區分缺失值和真實數據的情況。在空間狀態下，可以使用掩碼矩陣來表示數據的缺失狀態。在復雜的實際環境中，可能無法對歷史數據進行數據插補并順序預測未來的交通狀態，因為當交通狀態數據量巨大且設備的計算能力受到限制時，它將無法應付長期連續的數據丟失。在這些情況下，可以使用掩碼矩陣來表示缺失值。交通狀態數據可以通過使用檢測器檢測車輛來收集。當檢測器發生故障或未檢測到車輛通過道路時，收集的交通狀態數據可能會出現缺失值。由于交通網絡是一個動態系統，在車輛的運動過程中，各個環節的狀態不斷變化，在收集的交通數據中存在缺失值時，使用一系列掩碼矩陣m t∈?1×n，其中m t表示交通狀態序列x t中缺失值的位置。掩碼矩陣的某一個元素可以表示為：

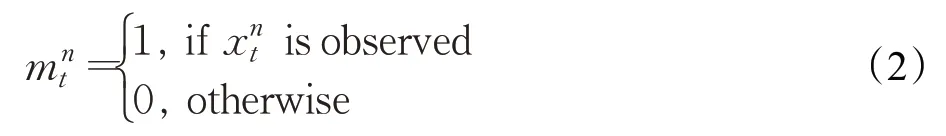
1.3 卷積神經網絡

完整的卷積神經網絡主要由模型輸入、特征提取、預測和模型輸出四部分構成。如圖3所示，首先將檢測器所捕獲的數據根據掩碼矩陣和時空矩陣的特征輸入模型，通常將模型的輸入數據表示為在t時間有一個交通時間序列矩陣，以下表示的是模型輸入矩陣X t，如下所示：

圖3 時空卷積神經網絡模型Fig.3 Spatial-temporal convolutional neural network model

流量序列數據的范圍是從t-L+1到t。時間序列以時空矩陣x t和掩碼矩陣m t的形式集成，其次是通過卷積層和池化層進行交通狀態特征的提取，在進行模型訓練前首先要初始化卷積層和輸出層的卷積核即權重和偏置。卷積層的參數是一些濾波器的集合，可以提取多個交通流量特征，也可以看作是神經元的輸出，通過權值共享可以降低參數的數量，以提取更高層次和更抽象的流量特征。其卷積操作可表示為如下：

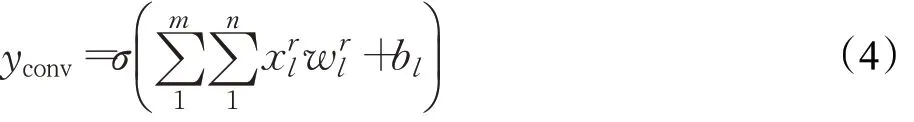
其中，σ是激活函數，進行卷積操作，是第l個時間單位在r個檢測器的交通狀態，r∈[1,m]，l∈[1,n]，為權重，b l為卷積層的偏差。

接下來是池化層，其目的是為了簡化卷積層的輸出，降低數據體的空間尺寸。其池化操作可表示為如下：

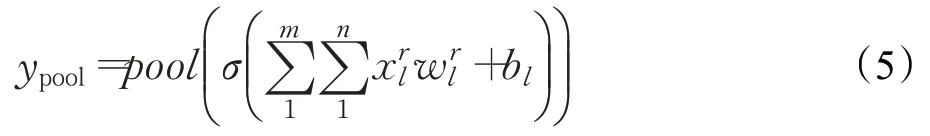
最后通過一個全連接的層將該向量轉換為模型輸出，因此，模型的輸出可以表示為：

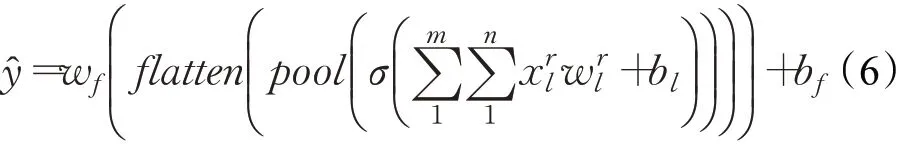
其中，w f和b f為全連接層的權重和偏差，y?是預測的交通流量。

該模型的目標是找到一個映射函數，以滿足ypool到y?之間的轉換，并輸出預測結果，其中變量的定義和范圍與上述變量相同。由于輸入數據的不同維度，例如小時通常在0到23之間，而交通速度通常限制在60 m/s左右。

2 實驗分析

實驗選取METR-LA和PEMS-BAY兩個真實的數據集來對模型的性能和效率進行評估[6]，METR-LA交通數據集包含從洛杉磯縣高速公路上的線圈檢測器產生的交通狀態數據，收集了從2012年3月1日至2012年6月30日的4個月的實驗數據。PEMS-BAY數據集由加州運輸機構（加州跨線）性能測量系統收集，收集了2017年1月1日至2017年5月31日的6個月的實驗數據。由于這兩個數據集規模較大，數據比較全面，交通流狀況復雜，具有一定的代表性，是交通流預測的理想選擇。在本實驗中將數據集分為訓練集、驗證集和測試集，各個數據集所占比例為6∶2∶2。

2.1 評估指標

所有測試模型的預測準確性均通過3個指標進行評估，包括平均絕對誤差（MAE）、平均絕對百分比誤差（MAPE）和均方根誤差（RMSE）。計算公式如式（7）～（9）所示[4]：

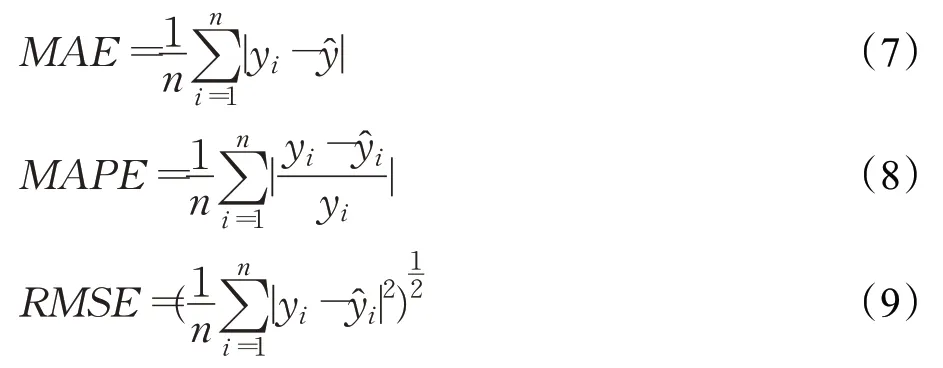
其中，yt是t時間點交通數據的真實值，是同一時間點的預測值，n表示捕獲的交通數據量個數。

2.2 模型參數

在卷積神經網絡模型中，學習率、批量大小、訓練迭代次數等參數的選擇對實驗結果有很大的影響。學習率決定了模型中權值更新的速度，批量大小為模型訓練過程中的一次處理的樣本的數量，迭代次數表示在一個訓練集上學習的次數。經過多次預訓練和優化調整，將學習率設置為0.01，批量大小設置為64。在本文實驗中，所提出的模型在METR-LA數據集上迭代90次時學習誤差趨于穩定，在PEMS-BAY數據集上迭代110次時誤差指標趨于穩定。

2.3 數據缺失模擬

PEMS-BAY和METR-LA數據集最初存在缺失值，其缺失值百分比分別為0.003%和8.11%，為了測試模型在不同缺失率情況下的性能表現，在數據集原始缺失的基礎上，根據特定的缺失比率將數據集中的部分數值隨機設置為零，并相應地生成掩碼矩陣進行圖像模擬。使用這兩個數據集進行數據隨機缺失和連續缺失的模擬。

PEMS-BAY數據集數據隨機缺失模擬如圖4所示，圖（a）表示數據隨機缺失率為10%的圖像，圖（b）表示數據隨機缺失率為20%的圖像，圖（c）表示數據隨機缺失率為30%的缺失情況的圖像。圖像中黑色的像素點表示數據缺失情況，在圖像中隨機分布的黑色像素點表示為離散分布，從圖中可以看出隨機缺失率越大，圖像中的黑色像素點越多。

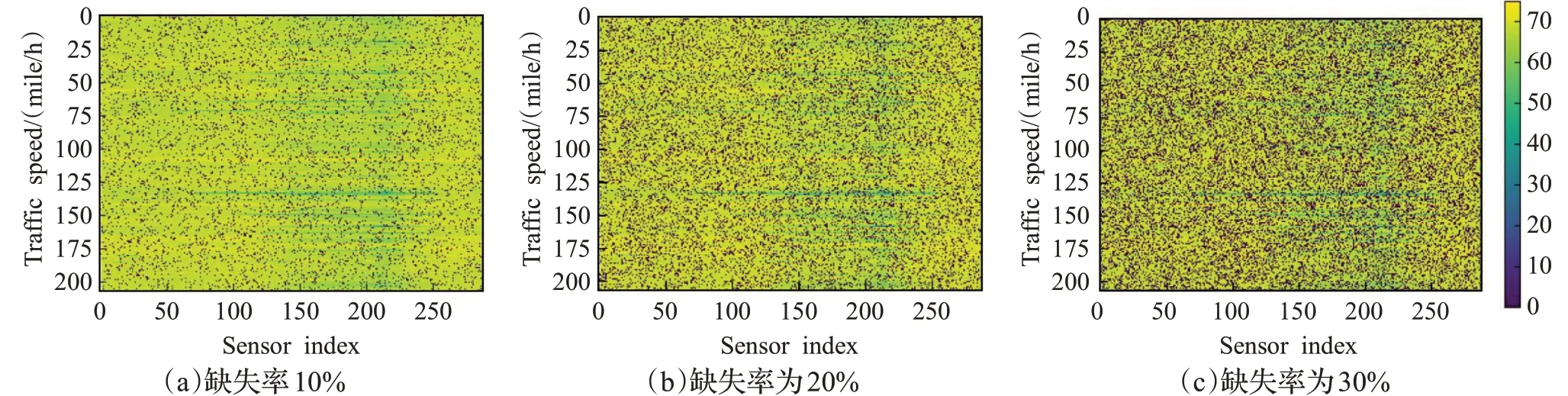
圖4 PEMS-BAY數據集隨機缺失數據模擬結果Fig.4 Simulation of random missing data in PEMS-BAY dataset

METR-LA數據集連續缺失的數據模擬如圖5所示，圖（a）為數據連續缺失率為10%時的圖像，圖（b）表示數據連續缺失率為20%時的圖像，圖（c）表示數據缺失率為30%時的圖像，從圖像中黑色像素點的分布情況可以看出，當數據時連續缺失時，圖像中的黑色像素點表示為線性分布，數據連續缺失率越大，圖像中呈現為黑色的像素點越多。

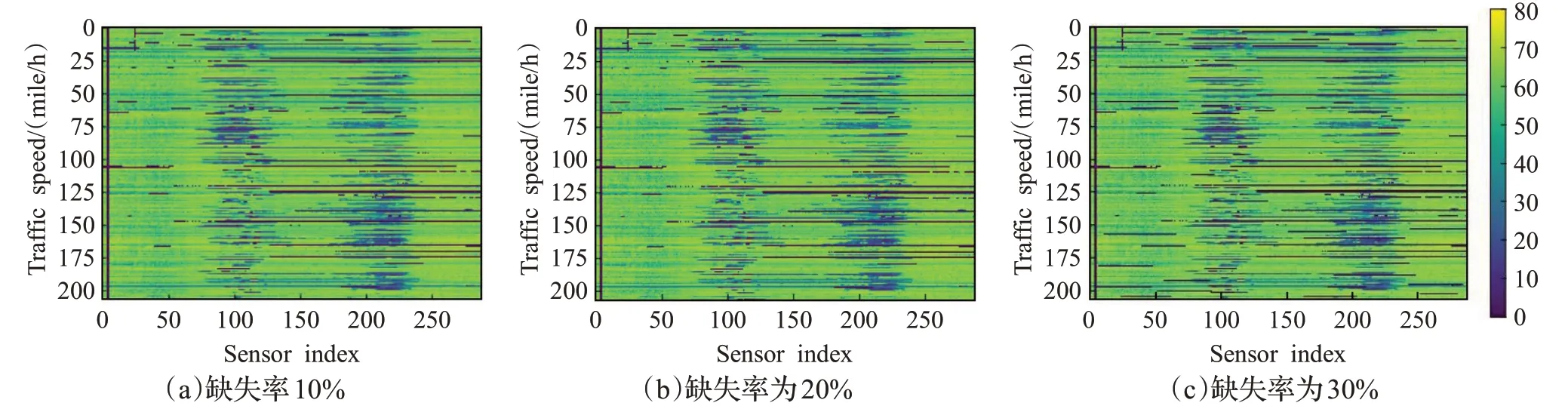
圖5 METR-LA數據集連續缺失數據模擬結果Fig.5 Simulation of continuously missing data in METR-LA dataset

2.4 不同日期的交通流預測

選取PEMS-BAY數據集中的測試數據輸入到訓練好的ST-CNN模型中，生成預測結果，將2017年2月和3月的數據集用作訓練集；2017年4月和5月的數據用作模型優化的數據集；2017年6月的數據作為測試集。2017年6月23日（工作日）的預測和評估結果如圖6（a）所示，2017年6月25日（非工作日）的預測和評估結果如圖6（b）所示。其中圖6（a）的上部表示的是周內的預測結果和真實值的曲線擬合圖，下部表示的是每個時間點的預測值和真實值的絕對誤差（AE）；圖6（b）的上部表示的是的是周末的預測結果和真實值的曲線擬合圖，下部表示的是每個時間點的預測值和真實值的絕對誤差（AE）。

從圖6中可以看出，工作日和非工作日的交通流量有些差異，但使用ST-CNN模型可以很好地識別出其發展的規律和特征，其交通流的預測結果在真實值周圍的波動幅度較小，并且其絕對誤差最大為3 mile/h，預測誤差的絕對值在合理的范圍之內。

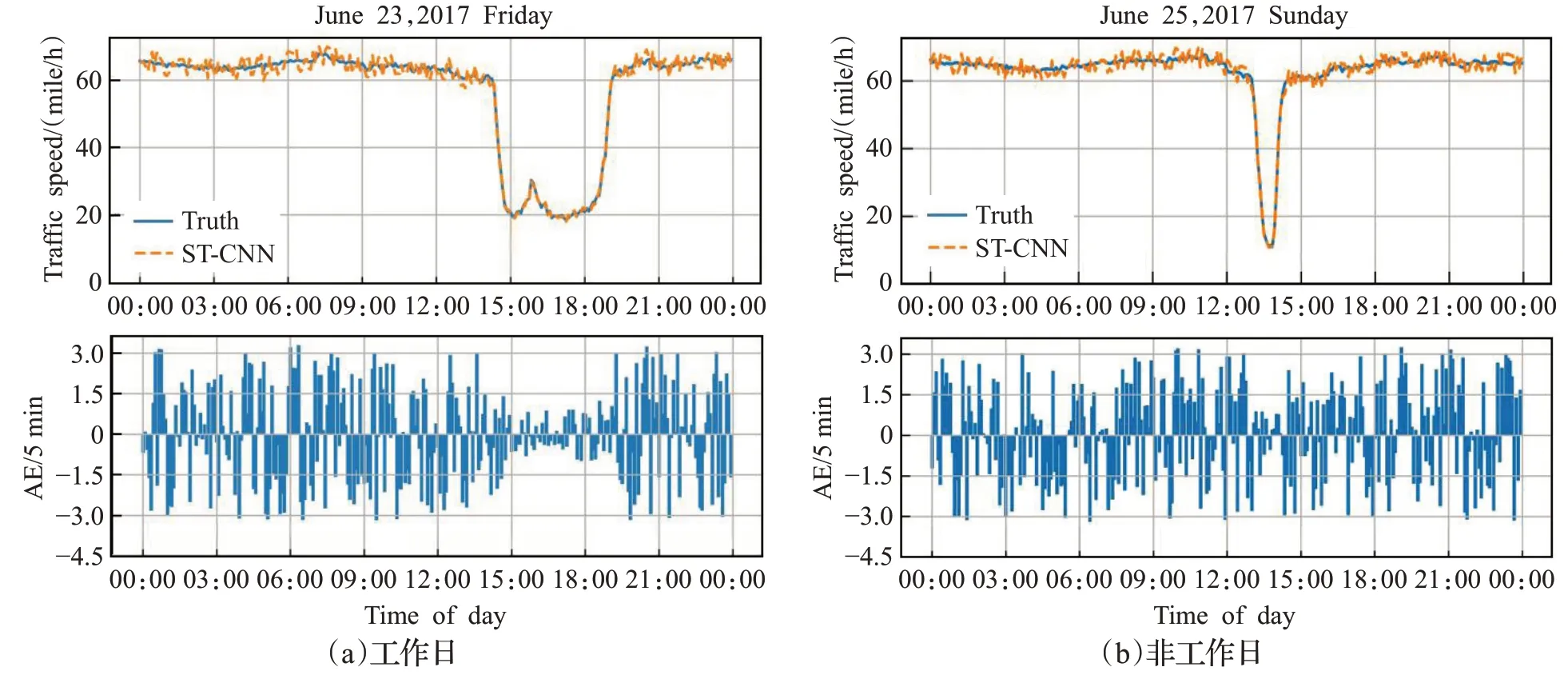
圖6 不同日期交通流預測結果Fig.6 Traffic flow speed prediction results of different dates

2.5 不同位置的交通流預測

選取PEMS-BAY數據集中的測試數據輸入到訓練好的ST-CNN模型中，生成預測結果，將2017年2月和3月的數據集用作訓練集；2017年4月和5月的數據用作模型優化的數據集；2017年6月的數據作為測試集。2017年6月23日12：00（工作日）的不同檢測器上的交通流的預測和評估如圖7（a）所示，2017年6月25日12：00（非工作日）的不同檢測器上的交通流的預測和評估如圖7（b）所示。其中圖7（a）的上部表示的是的是周內的預測結果和真實值的曲線擬合圖，下部表示的是每個時間點的預測值和真實值的絕對誤差（AE）；圖7（b）的上部表示的是的是周末的預測結果和真實值的曲線擬合圖，下部表示的是每個時間點的預測值和真實值的絕對誤差（AE）。

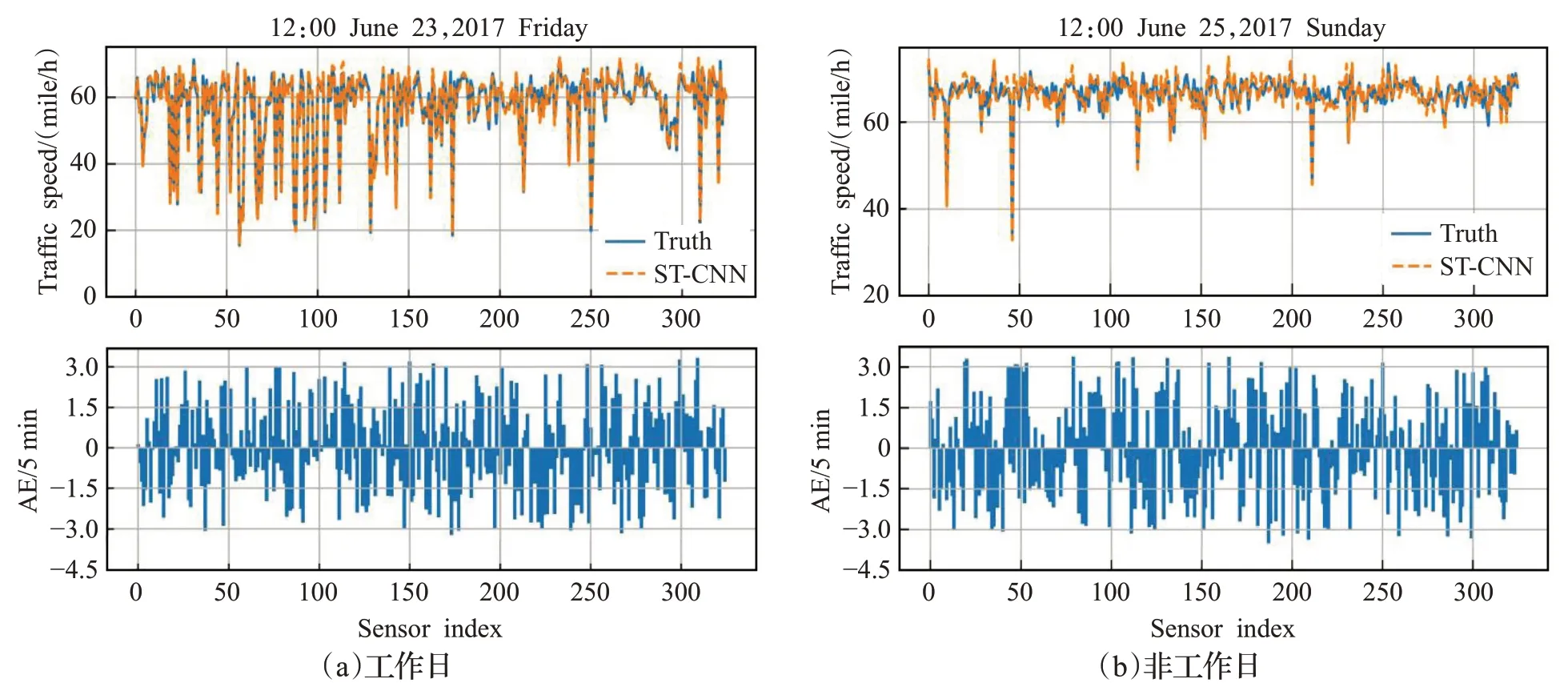
圖7 不同檢測器交通流預測結果Fig.7 Traffic flow speed prediction results of different sensors

從圖7中可以看出，工作日和非工作日的交通流量有些差異，但使用ST-CNN模型可以很好地識別出其發展的規律和特征，其交通流的預測結果在真實值周圍的波動幅度較小，并且其絕對誤差最大為3 mile/h，預測誤差的絕對值在合理的范圍之內。

2.6 不同預測模型的交叉驗證

為了更好地驗證ST-CNN模型的優越性，選取在交通流預測中應用較為廣泛的GRU、LSTM、DCRNN和GMN模型作為對比預測模型。

（1）GRU：門控單元循環網絡[4]，可以捕獲時間序列中的長期時間依賴性，主要模型參數隱藏單元數目是64，梯度下降算法是Adam（adaptive moment estimation），輸入時間步長是12。

（2）LSTM：長短期記憶網絡[5]，可以克服梯度爆炸或消失問題，主要模型參數隱藏單元數目是64，梯度下降算法是Adam，輸入時間步長是12。

（3）DCRNN：擴散卷積循環神經網絡[6]，可以捕獲路網數據的交通依賴，主要模型參數包括：隱藏單元數目是64，梯度下降算法是Adam，輸入時間步長是12。

（4）GMN：圖馬爾可夫神經網絡[7]，可以進行時空數據預測，可以用鄰接矩陣表示交通網絡的拓撲結構。

在實驗中，所有測試模型的預測結果都通過平均絕對誤差（MAE）、平均絕對百分比誤差（MAPE）和均方根誤差（RMSE）進行評估。在數據缺失率為10%、20%和30%的情況下，模型的預測結果如表1和表2所示。

表1和表2分別展示了在PEMS-BAY和METR-LA數據集上測試的不同缺失率下的預測結果。通過對比不同模型在不同缺失率下的預測結果，發現實驗結果在三類指標下的表現均優于其他對比模型，在MAE指標降低的同時，MAPE和RMSE指標也在降低，在交通流數據缺失率增大的情況下，該模型仍然有效，其性能指標對比于其他模型來說仍然最優越。這是因為GRU、LSTM、GMN這些模型主要是根據時間序列的預測，捕獲的是交通流數據的事件相關性，在獲取空間關系的相關性上表現較差。本文提出的ST-CNN模型，通過建立時空矩陣，引入掩碼矩陣來表示數據的缺失狀況下的交通流預測，在缺失率為10%、20%和30%上都取得了最好的預測結果，充分說明了ST-CNN模型的正確性、有效性和廣泛的適應性。同時，大多數交通流預測都是通過插補法解決少量的交通數據的隨機缺失，當數據連續缺失時，預測精度會降低，從表1和表2中可以看出，隨著缺失率的增高，以上模型的MAE、MAPE和RMSE這幾類誤差值也在增大，因此可以看出，缺失率越高，預測的精確率越低。

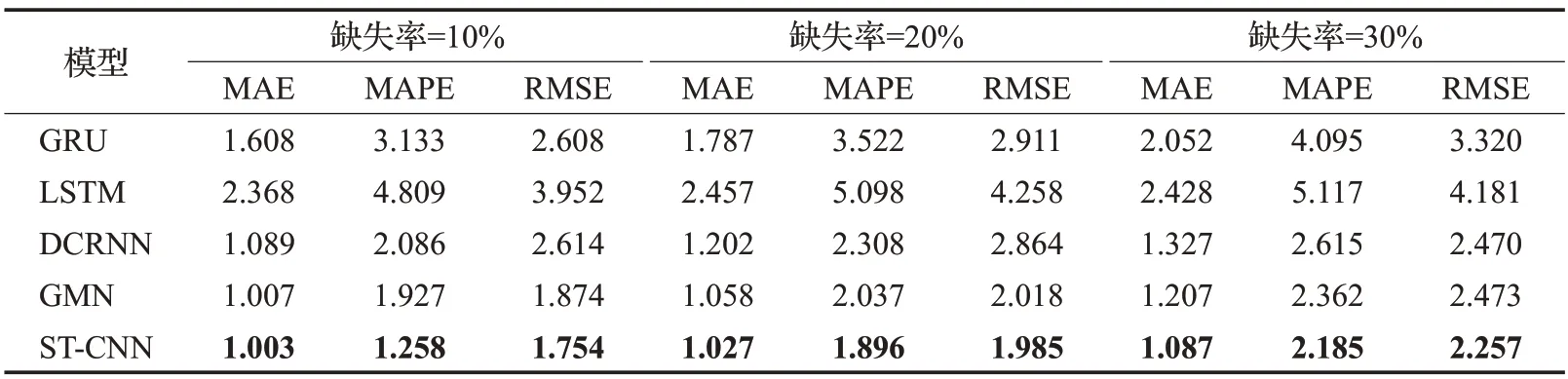
表1 PEMS-BAY數據集3種缺失情況下的預測結果Table 1 Prediction results in 3 missing cases of PEMS-BAY dataset

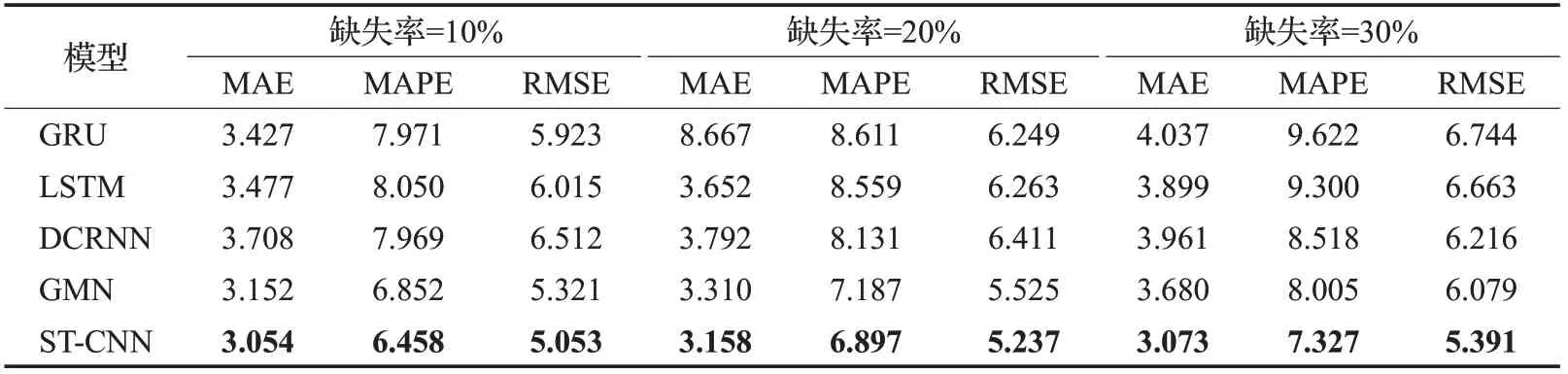
表2 METR-LA數據集3種缺失情況下的預測結果Table 2 Prediction results in 3 missing cases of METR-LA dataset

在PEMS-BAY數據集中任取一天的預測數據，將各模型的預測結果與真實數據進行對比，結果如圖8所示。從圖中可以看出，相對于LSTM、GMN模型來說，ST-CNN預測結果更加準確，其結果更接近真實值。

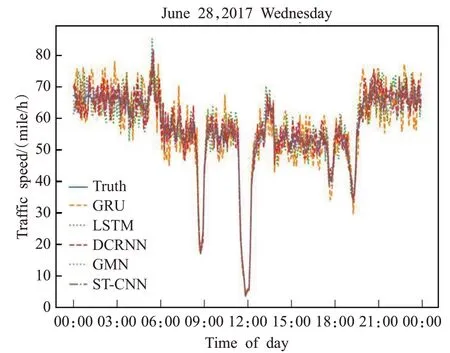
圖8 不同模型5 min交通流預測結果Fig.8 Traffic flow speed prediction results of different models in 5 min interval

3 結論

本文利用交通流數據的時空相關性和時間序列的連續性特征，構建了路網交通數據時空矩陣和掩碼矩陣，提出了一種基于時空卷積神經網絡的交通流預測方法，實現了在數據連續缺失情況下的交通流預測。與多種先進的模型預測對比表明，該模型能夠更好地挖掘交通流的時空關系，提高了在數據缺失情況下的交通流的預測精度。同時，利用時空矩陣和掩碼矩陣可以更好的模擬出了交通數據的趨勢狀態，在數據缺失的情況下能夠有效地預測交通流的發展趨勢，提升了交流的預測效率，為智能交通系統提供了理論支持，對交通管制和交通路況信息分析具有重要的理論意義和參考價值。

本文提出的時空卷積預測模型僅在公開的高速公路數據集進行了實驗驗證工作，未來研究中，將會引入城市內部交通流數據，對交通數據進行全面分析驗證，并且考慮影響交通流的外部環境因素，從而進一步優化完善模型的結構和預測性能。