不同定子繞組結構五相感應電機開路故障時性能對比分析

范舒婷 孟大偉 艾萌萌

不同定子繞組結構五相感應電機開路故障時性能對比分析

范舒婷 孟大偉 艾萌萌

（哈爾濱理工大學電氣與電子工程學院 哈爾濱 150080）

為研究不同繞組結構對五相電機的影響，在現行單繞組及星形-五邊形組合繞組的基礎上，該文提出三種新型組合繞組：五邊形-星形繞組、五角星-星形繞組與星形-五角星繞組。首先，建立繞組磁動勢模型與電壓不平衡系數（VUF）計算模型，利用有限元方法計算電機繞組磁動勢（MMF）諧波含量、電壓不平衡系數。其次，制作15kW五相感應電機，并以此為樣機對不同繞組結構五相感應電機開路故障下的穩態性能進行分析。仿真及實驗結果表明，對于單繞組結構，開路狀態下五邊形繞組最有利于電機運行；而對于組合式繞組，該文提出的五邊形-星形繞組相比于現行的星形-五邊形繞組，既有磁動勢諧波含量低的優點，又可以進一步減小電壓不平衡系數，提高可帶負載轉矩，更有利于電機在開路情況下運行。

五相電機 組合繞組 開路故障 最大轉矩倍數 電壓不平衡系數

0 引言

隨著大功率電力電子技術的不斷發展，感應電機具有的結構簡單、運行可靠、維修便捷、起動性能好和調速范圍廣等特點[1]。大容量的多相感應電機在航空、船舶、電動汽車等領域的備受關注[2-4]。電機作為驅動系統中的重要組成部分，其性能對系統的穩定性具有重要影響。五相電機具有轉矩波動小、效率高、容錯性能好等優點[5]。對比六相電機[6-7]，五相電機故障后能提供更大的負載轉矩，電機一相開路并采取最優電流控制時，所帶負載可以達到額定負載的70%[8]。近年來，對于五相電機的研究開始走熱，并集中在電機的容錯控制、減小轉矩脈動方面[9-10]。但關于五相電機繞組理論方面的研究國內少之又少，且針對五相電機的研究多集中在星形繞組，對其他繞組聯結方式五相電機的研究十分有 限[11-12]。目前，五相電機領域處于技術發展期，對五相電機的研究具有重要的理論價值和實際意義。

五相電機有三種單繞組聯結方式[13-14]，不同繞組聯結方式五相電機在發生開路故障下的容錯性能不同。S. A. Ayman等通過對比在正常運行和一相開路情況下采用開環控制和最優電流控制方法時星形繞組與五邊形繞組的特性曲線，證明星形繞組在健康運行時銅耗小，五邊形繞組在一相開路下降額系數小[15]，但該研究沒有涉及五角星繞組，對一相開路下三種單繞組聯結方式五相電機的研究并不充分。I. M. Mahmoud等證明了單繞組中五邊形繞組發生開路故障后的電壓不平衡系數（Voltage Unbalanced Factor, VUF）最小[16]，但僅考慮電壓不平衡系數不能綜合評價三種單繞組在開路情況下的容錯性能，需多個開路故障下參數綜合進行判斷。Z. Pavel等通過分析電機定轉子電流在矢量空間的運動軌跡，推導出一相開路下五角星繞組感應電機電磁轉矩脈動的波形[17]，該方法應用于星形繞組與五邊形繞組還未有相關成果。為綜合不同繞組聯結五相繞組的優點，將兩條繞組支路在空間上相差一定角度構成組合繞組視為一種研究方向。

目前，針對五相電機組合繞組的文獻還較少。S. A. Ayman等為了使電機同時具有星形繞組與五邊形繞組的優點，通過將電機繞組分為兩套繞組支路，提出了星形-五邊形組合繞組[18]。繞組內部的相帶分布與十相繞組相同，外部僅有5個出線端。通過建立電機的穩態模型[19]和動態模型[20]，證明一相開路后，這種組合式繞組同時具有星形繞組可消除三階諧波磁通分量和五邊形繞組降額系數小的優點。但根據已有文獻，關于五相電機組合繞組的研究局限于星形-組合繞組，通過將兩條繞組支路在空間上相差一定角度構成其他形式組合繞組還未有研究涉及。

為充分研究繞組聯結方式對五相感應電機的影響，本文提出五邊形-星形繞組、五角星-星形繞組和星形-五角星繞組三種新型組合繞組。以本文制作15kW電機為樣機，通過有限元方法計算繞組磁動勢（Magnetic Motive Force, MMF）諧波含量及負載狀態下一相開路時各繞組磁動勢分布；建立了對稱分量變換下電機開路后的穩態模型，包括一相開路、相鄰兩相開路及非相鄰兩相開路；并基于IEC標準，計算電壓不平衡系數。最后通過實驗測量各繞組形式電機一相開路后的電流，進而計算出電機磁動勢分布。結果表明，組合繞組電機健康運行時磁動勢諧波含量更少，相比于現行的星形-五邊形繞組，五邊形-星形繞組在三種開路情況下開路后的磁動勢分布更接近圓形，電壓不平衡系數更小，更有利于電機在開路下運行。

1 繞組聯結方式

五相電機定子繞組根據聯結方式分為兩類：單繞組和組合繞組。單繞組包括星形繞組、五邊形繞組和五角星繞組；組合繞組由在空間上相差一定角度的兩條繞組支路構成，內部相帶分布與十相繞組相同。為方便表述，將五相繞組分為10條支路：a1、b1、c1、d1、e1和a2、b2、c2、d2、e2。

1.1 單繞組聯結方式

單繞組各相繞組分別由相應兩條支路串聯構成，其相位差為72°，聯結方式如圖1所示。

定義star、pentagon、pentacle分別為星形繞組、五邊形繞組、五角星形繞組相電壓。忽略電源諧波分

量，設星形繞組相電壓為

式中，Vm為星形電壓幅值；w 為供電電源角頻率。

五邊形繞組相電壓為

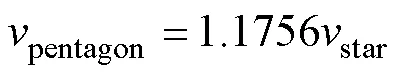
五角星繞組相電壓為

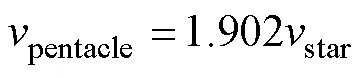
定義star、pentagon、pentacle分別為星形繞組、五邊形繞組、五角星形繞組每槽匝數。則

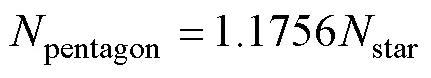
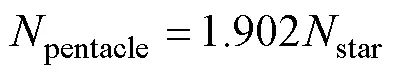
1.2 組合繞組聯結方式

改變兩條繞組支路端部連接可構成六種組合繞組模式。但五邊形-五角星和五角星-五邊形組合模式相應兩條支路的電壓矢量空間位置相同，不能構成可用的組合繞組。因此，本文只對圖2所示四種組合繞組模式進行研究。從空間排列上，a2、b2、c2、d2、e2支路分別滯后于a1、b1、c1、d1、e1支路18°。

定義a1、a2分別為a1繞組、a2繞組支路電壓。a1支路的電壓為

圖2 組合繞組聯結方式

為保證兩條支路產生的磁動勢相同，五邊形-星形繞組與星形-五邊形繞組中相應兩條支路電壓關系為

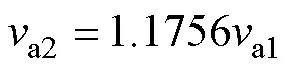
定義a1、a2分別為a1繞組、a2繞組每槽匝數。每槽匝數關系為

五角星-星形繞組與星形-五角星繞組的五角星支路電壓與星形支路電壓關系為

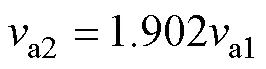
每槽匝數關系為

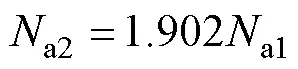
2 樣機參數及繞組磁動勢模型

2.1 五相電機樣機參數

以額定功率15kW的Y160L-4型三相異步感應電機為基準，保持電機額定功率與定、轉子內、外圓尺寸及氣隙長度不變的條件下，改變定轉子槽數配合以及定轉子槽形尺寸，并對定子繞組重新設計，制作了不同繞組結構的五相電機。表1與圖3為不同繞組結構的幾個規格五相感應電機與原三相感應電機的異同之處。

除表1與圖3所示的定轉子槽型尺寸外，五相電機樣機其余材料與尺寸均與Y160L-4型三相異步感應電機完全一致。

表1 五相電機與原三相電機異同的參數

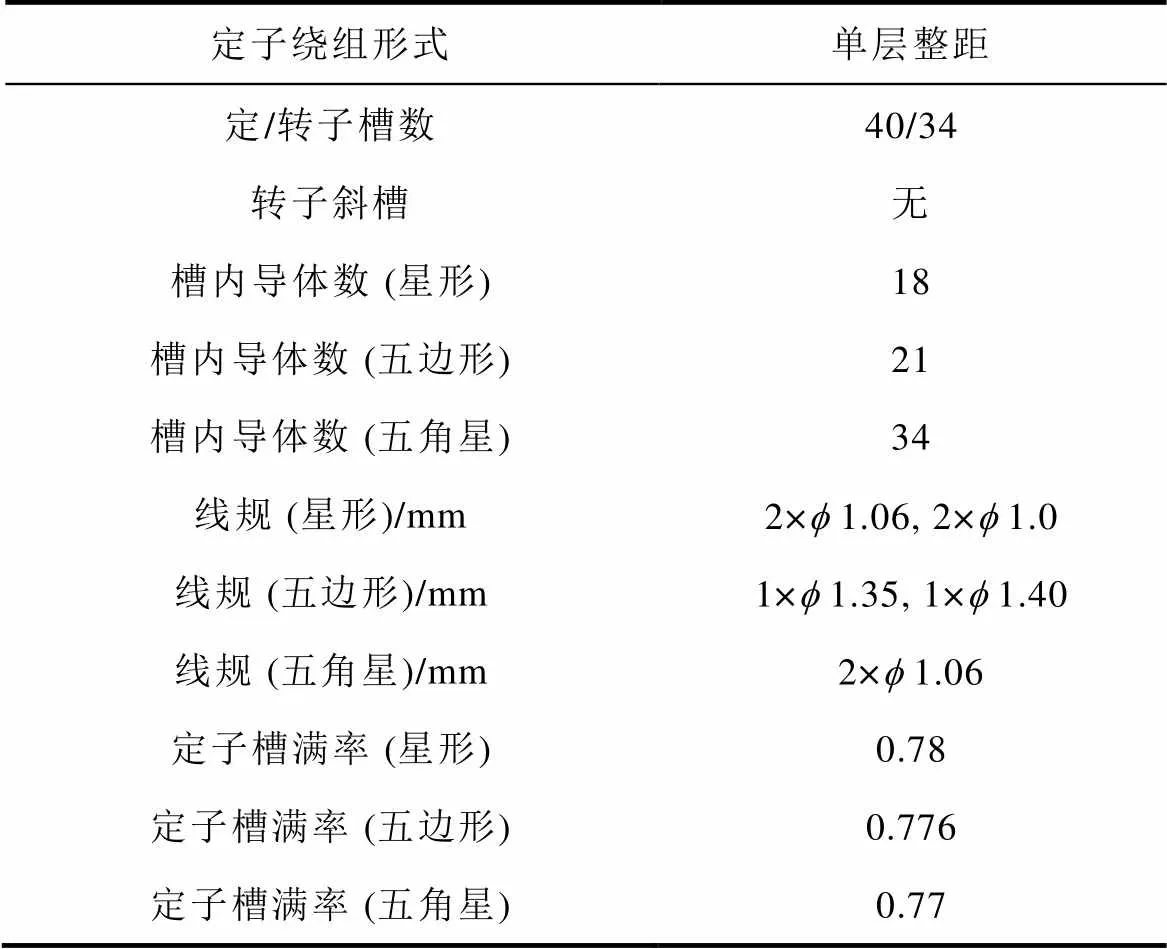
Tab.1 Differences of parameters between the five-phase motor and the three-phase motor

單位: mm

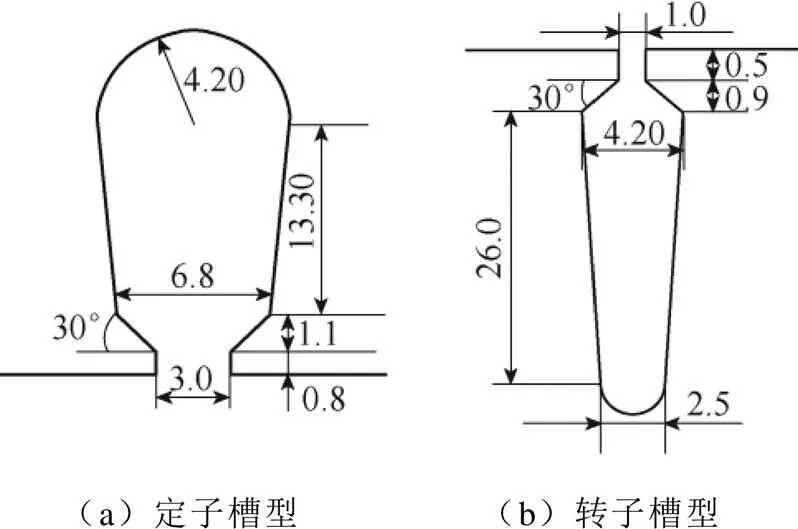
圖3 五相電機的定轉子槽形

對不同繞組聯結方式五相電機健康狀態進行仿真，電機磁通密度的有限元仿真模型如圖4所示。

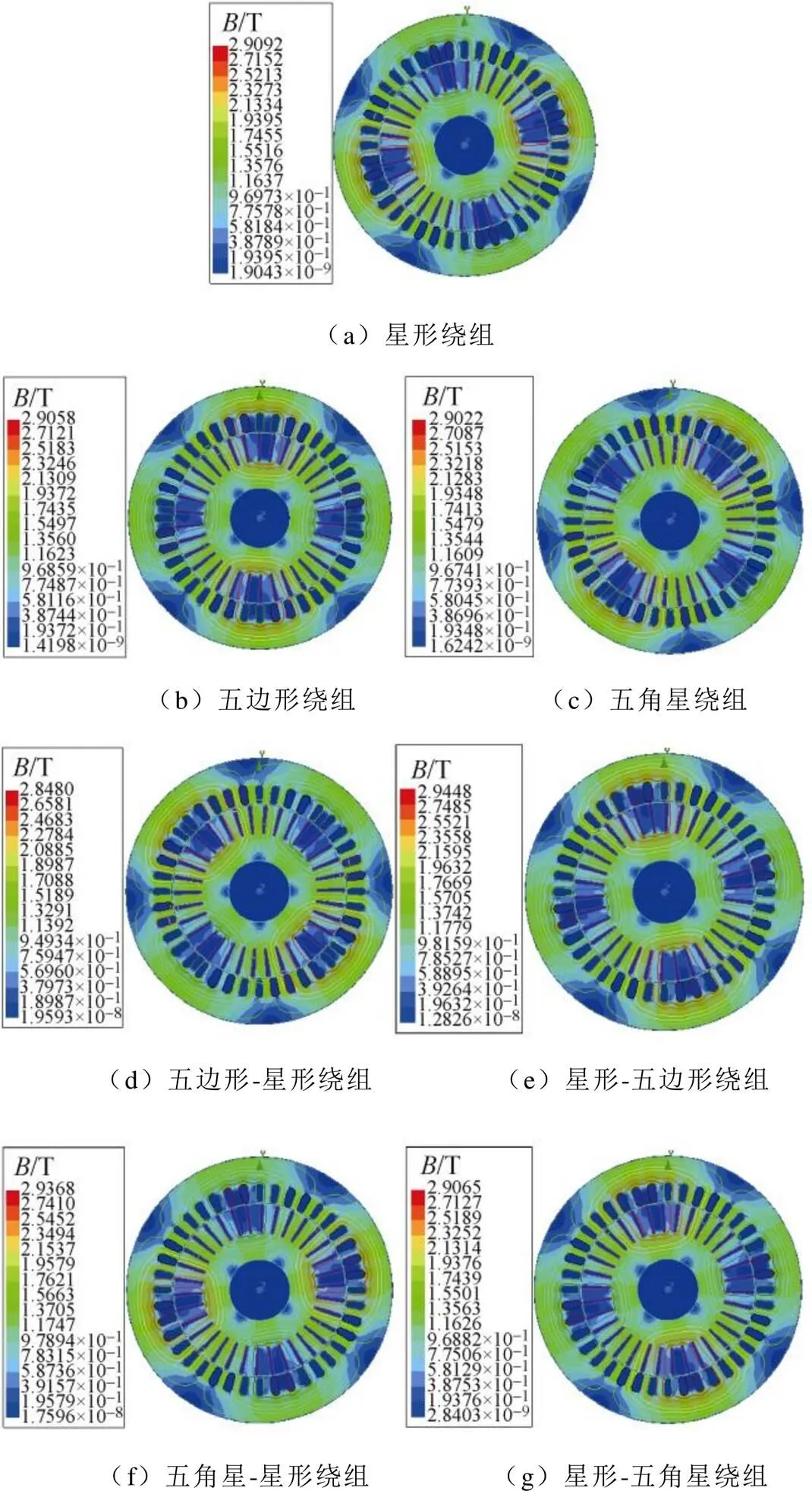
圖4 健康運行下磁通密度分布的有限元仿真

2.2 五相繞組磁動勢模型和故障時磁動勢分析

為研究繞組聯結方式對磁動勢諧波含量及磁動勢分布的影響，建立各支路繞組函數。單繞組三種聯結方式產生的空間諧波相同，每相兩條繞組支路具有相同的時間諧波，故三種繞組產生的時空諧波磁動勢波形相同。以氣隙圓周運動角度為橫軸，設a1支路在=0rad的位置，a1支路與a2支路的繞組函數1()、2()如圖5所示。

圖5 a1與a2支路繞組函數

不計電源諧波，單繞組各相繞組電流為

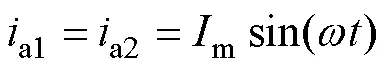
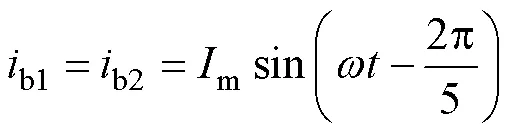
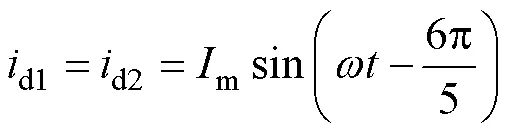
式中，m為單繞組支路電流幅值。

單繞組總磁動勢為

對于組合繞組各相支路電流為

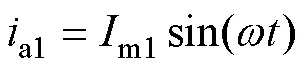
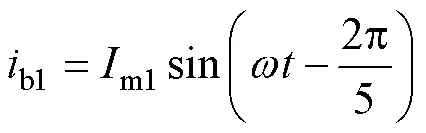
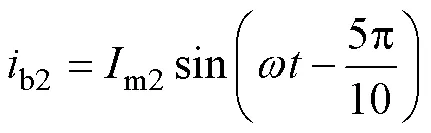
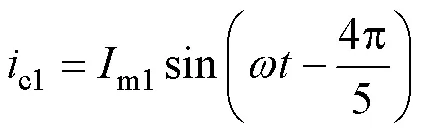
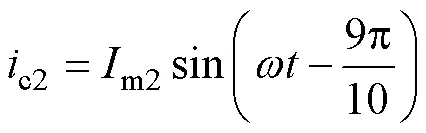
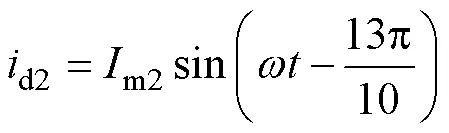
式中，m1、m2分別為a1、a2繞組電流幅值。組合繞組總磁動勢為

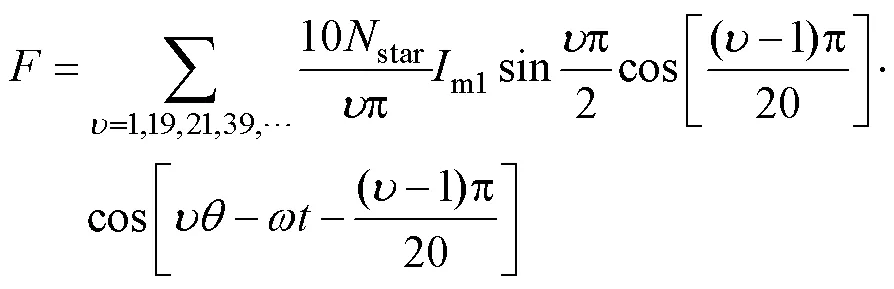
以星形繞組基波磁動勢為1單位，單繞組與組合繞組氣隙磁動勢空間諧波含量見表2。

表2 氣隙磁動勢諧波含量

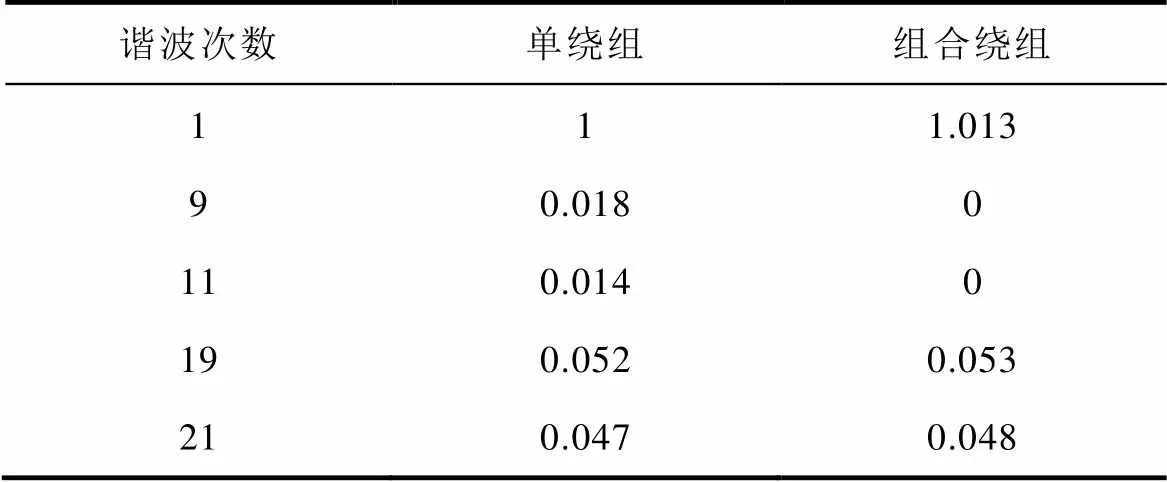
Tab.2 Air gap MMF harmonic content

由表2可知，電機健康運行時，組合繞組的氣隙磁動勢不包含9次與11次諧波，基波磁動勢為單繞組的1.013倍。

一相開路后，電機各相電流不對稱，磁動勢分布受電流影響不再呈圓形。對電機發生開路后的磁動勢分布進行仿真，設電機穩定運行后發生開路故障，負載轉矩保持為30N·m。假定一相開路時為E相故障，相鄰兩相開路時為D相與E相故障，非相鄰兩相開路時為C相與E相故障。根據有限元方法仿真電機故障后電流，并計算出三種開路故障下的磁動勢分布如圖6所示。

由磁動勢分布可見，組合繞組的磁動勢畸變程度與兩條支路的磁動勢畸變程度呈正相關。受五角星支路的影響，星形與五角星兩種組合繞組的磁動勢畸變程度高；而受五邊形支路的影響，星形與五邊形兩種組合繞組的磁動勢畸變程度低。

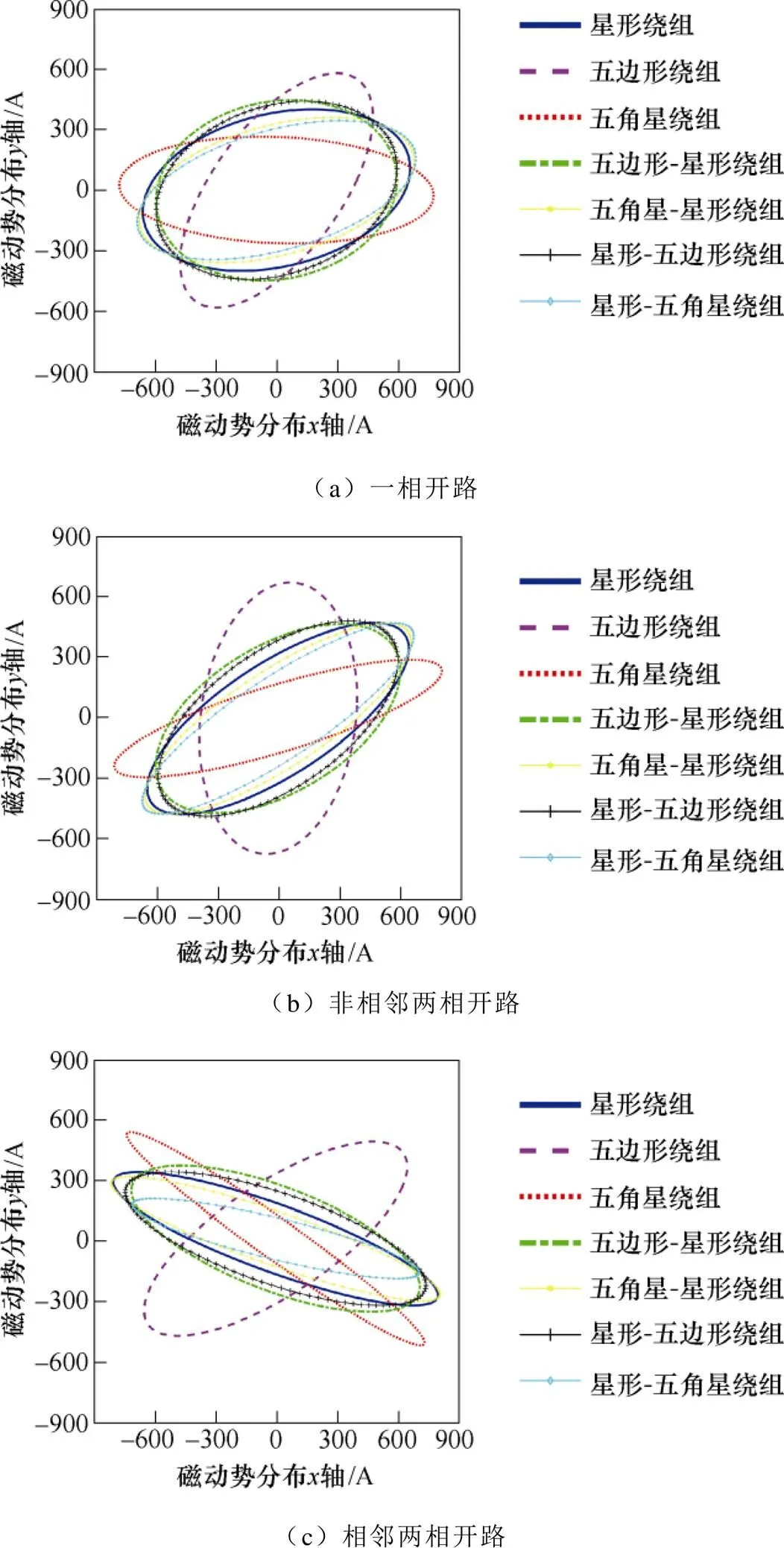
圖6 磁動勢分布

相比于其他單繞組聯結，五邊形繞組磁動勢三種開路故障狀態下的畸變程度低，有利于電機運行。文獻[15]證明，星形-五邊形繞組在一相開路下既有較好的磁通分布，也具有磁動勢諧波含量少的優點；與之相比，本文提出的五邊形-星形繞組除了上述優點外進一步減小了電機的磁動勢畸變。

3 電壓不平衡系數

電機開路故障后，各支路電壓不再對稱，以電壓不平衡系數來評價電機故障后的表現。根據IEC國際電工委員會給出的電壓不平衡系數定義[13]，有

采用對稱分量變換建立穩態運行數學模型，將對稱循環矩陣變為對角陣，各維度的方程為獨立關系，構成一端口網絡。根據繞組各序向量圖，對稱分量變換矩陣為

式中，為對稱分量變換矩陣；1為繞組間電角度，1=2p/5。每相電壓和序電壓關系為

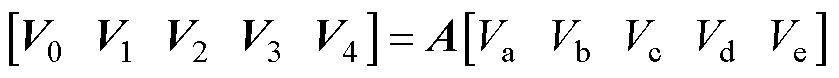
式中，0為零序電壓分量；1為正序電壓分量；4為負序電壓分量；2、3為第三序平面的電壓分量；a～e分別為A～E相相電壓。

組合繞組相應兩條支路電壓不同，利用式（29）和式（30）分別計算支路電壓不平衡系數，取平均值為組合繞組電壓不平衡系數，有

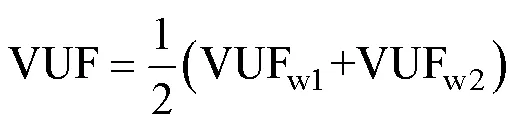
式中，VUF為總電壓不平衡系數；VUFw1為第一套繞組電壓不平衡系數；VUFw2為第二套繞組電壓不平衡系數。

電機開路故障后帶載能力降低，為計算電機開路后從空載到最大轉矩倍數的電壓不平衡系數，先通過有限元方法得出不同繞組聯結的電機最大轉矩倍數見表3。

表3 最大轉矩倍數

Tab.3 Max torque ratio

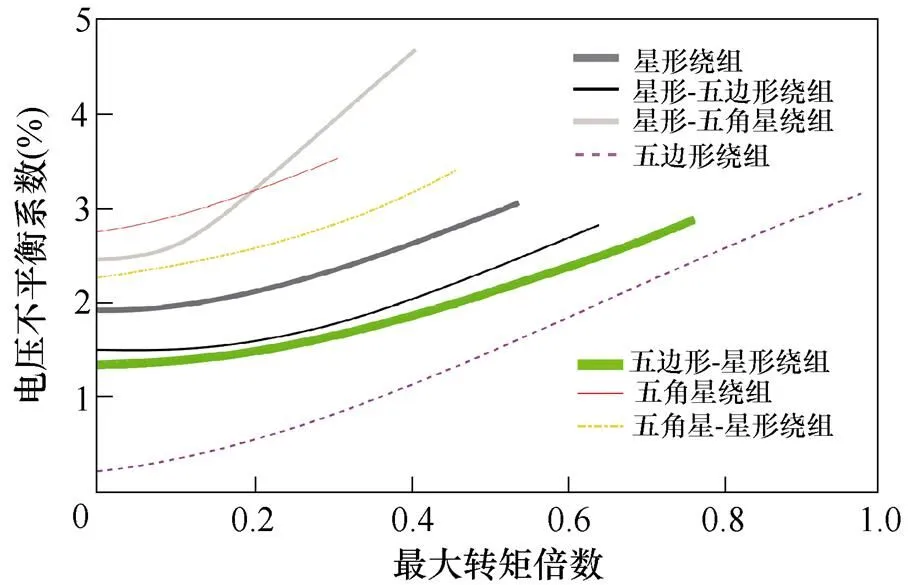
根據表3計算出三種開路故障下電機從空載到最大轉矩倍數的電壓不平衡系數曲線如圖7所示。

根據表3與圖7可知，單繞組聯結方式中五邊形繞組的最大轉矩降額最低、電壓不平衡系數最小；組合繞組聯結方式中，五邊形-星形繞組的最大轉矩降額最低、電壓不平衡系數最小。總體而言，在三種開路故障狀態下，后者稍遜于前者。然而，文獻[11]已經證明星形與五邊形組合繞組同時具備健康狀態星形繞組運行效率高和五邊形繞組開路故障時容錯能力強的特點，有綜合優勢。相比之下，本文提出的五邊形-星形繞組在三種開路故障狀態下都進一步減小了最大轉矩倍數的降額及最大電壓不平衡系數，更具優勢。

（a）一相開路

（b）非相鄰兩相開路

（c）相鄰兩相開路

4 實驗驗證

為驗證不同繞組聯結方式對五相感應電機的影響，對樣機進行一相開路實驗，電機所帶負載為30N·m。為保證電機額定輸出功率為15kW以及符合式（1）～式（3）的相電壓關系，各繞組聯結方式下變頻器供電的線電壓分別為：星形繞組、五邊形繞組、星形-五邊形繞組與星形-五角星繞組為252V；五角星繞組為409V；五邊形-星形繞組為126V；五角星-星形繞組為204.5V。電機起動正常穩定運行后，令E相開路，測量電機開路后的穩態電流。五相感應電機實驗設備如圖8所示。各繞組支路電流如圖9所示，并用引線將繞組電流各相引出標記。

圖8 五相感應電機實驗設備

圖9對由實驗設備產生的諧波電流進行處理，根據各相電流值計算出一相開路下電機磁動勢分布如圖10所示。

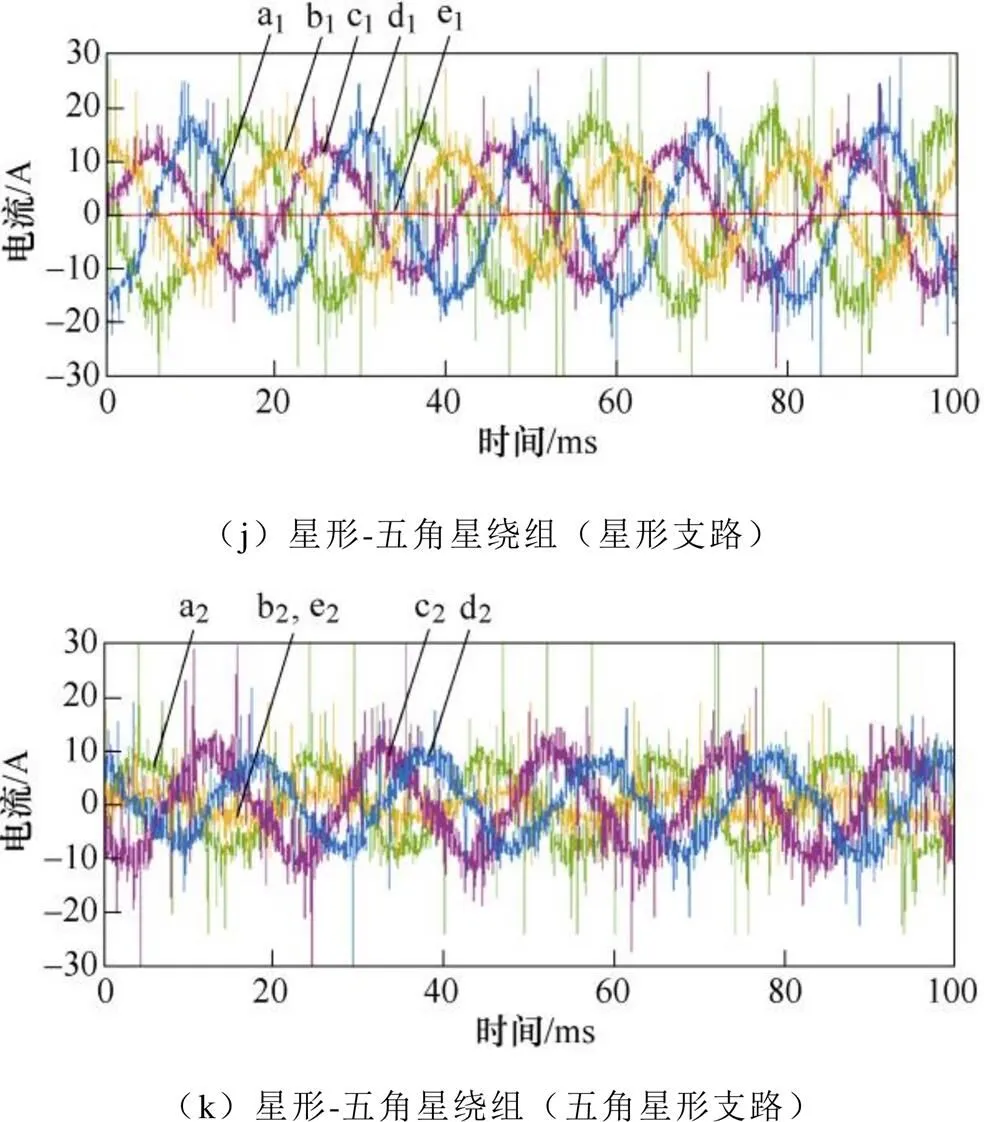
圖9 一相開路各支路電流

圖10 一相開路下磁動勢分布

圖9中各繞組支路電流表明，電機的供電端斷開，電機各相相電壓不再對稱，各相電流大小不同。一相開路后：星形繞組e1、e2繞組不是通路，電流為0，其他四相繞組不對稱，中性點不為0，各相繞組電流幅值不再相等。五邊形繞組d1、d2與e1、e2繞組相當于串聯，兩端電壓不為0，兩相電流重合。五角星與五邊形繞組相似，b1、b2與e1、e2繞組相當于串聯，兩端電壓不為0，兩相電流重合。星形-五邊形繞組星形繞組支路中，a1相繞組不是通路，電流為0，c2、d2兩相繞組串聯，電流重合，且各相鄰兩端電源之間繞組不再對稱，各相電流不再對稱，幅值不同。星形-五角星繞組與星形-五邊形繞組類似，星形支路開路電流為0，b2、e2電流重合，其余各相電流不一致。五邊形-星形繞組c2與d2兩端電壓不為0，繞組中點電位不為0，故繞組e1相電壓不為0，e1相電流不為0。五角星-星形繞組與五邊形-星形繞組類似，b2與e2兩端電壓不為0，e1相電壓不為0，故e1相電流不為0。

由圖10一相開路下磁動勢分布對比圖6a可知，兩者分布大體一致，說明仿真模型與結果是正確的。圖10仿真結果包含諧波磁動勢，這是由于各繞組聯結方式不同。根據圖9，一相開路后各相電流中電流大小與相位不對稱，電流中的高次諧波電流產生的諧波磁動勢不能抵消，疊加在基波磁動勢中，導致電機的磁動勢分布不為圓形。根據圖中的磁動勢分布，盡管五邊形繞組在電壓不平衡系數和最大轉矩倍數上有較好的表現，但五邊形-星形繞組在仿真下的磁動勢畸變程度低于五邊形繞組，更有利于電機在故障情況下運行。

5 結論

本文對五相感應電機各種可行的繞組結構在開路故障狀態下進行對比分析，得出以下結論：

1）組合繞組的性能受兩條支路的影響，星形與五邊形的兩種組合相比于星形與五角星的兩種組合，在開路故障下前者電壓不平衡系數低、最大轉矩倍數高、磁動勢基波畸變程度小。

2）在三種故障狀態下，五邊形繞組的最大轉矩降額最低、電壓不平衡系數最小，五邊形-星形組合繞組其次。但總體考慮健康狀態與開路故障狀態運行的綜合評價，星形與五邊形組合繞組更具優勢。而這兩種組合繞組對比，本文提出五邊形-星形繞組明顯優于現行的星形-五邊形繞組。

[1] 馬偉明. 關于電工學科前沿技術發展的若干思考[J]. 電工技術學報, 2021, 36(22): 4627-4636.

Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.

[2] 黃林森, 趙文祥, 吉敬華, 等. 穩態性能改善的雙三相永磁電機直接轉矩控制[J]. 電工技術學報, 2021, 37(1): 355-367.

Huang Linsen, Zhao Wenxiang, Ji Jinghua, et al. Direct torque control for dual three-phase permanent- magnet machine with improved steady-state perfor- mance[J]. Transactions of China Electrotechnical Society, 2021, 37(1): 355-367.

[3] 卜飛飛, 羅捷, 劉皓喆, 等. 雙繞組感應發電機系統無差拍電流預測控制策略[J]. 電工技術學報, 2021, 36(24): 5213-5224.

Bu Feifei, Luo Jie, Liu Haozhe, et al. Deadbeat predictive current control strategy of dual winding induction generator system[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5213-5224.

[4] 韓一, 聶子玲, 許金, 等. 雙三相非周期瞬態直線感應電機能量鏈切換控制策略[J]. 電工技術學報, 2021, 36(1): 258-267.

Han Yi, Nie Ziling, Xu Jin, et al. Energy chain switching control of a dual three-phase linear induction motor operating in non-periodic transient conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 258-267.

[5] 朱鵬, 喬鳴忠, 于飛, 等. 基于磁動勢平衡分析的多相感應電機容錯控制[J]. 電工技術學報, 2019, 34(增刊1): 62-69.

Zhu Peng, Qiao Mingzhong, Yu Fei, et al. Tolerant control for multi-phase induction motor based on magnetmotive force balance analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 62-69.

[6] 趙勇, 黃文新, 林曉剛, 等. 基于權重系數消除和有限控制集優化的雙三相永磁容錯電機快速預測直接轉矩控制[J]. 電工技術學報, 2021, 36(1): 3-14.

Zhao Yong, Huang Wenxin, Lin Xiaogang, et al. Fast predictive direct torque control of dual three-phase permanent magnet fault tolerant machine based on weighting factor elimination and finite control set optimization[J]. Transactions of China Electrotech- nical Society, 2021, 36(1): 3-14.

[7] 黃守道, 趙禮, 鄭劍, 等. 基于加權路徑內點法的六相電機SVPWM四矢量調制方法[J]. 電工技術學報, 2019, 34(2): 264-274.

Huang Shoudao, Zhao Li, Zheng Jian, et al. Four- vector modulation method for six-phase motor SVPWM based on interior point algorithm of weighted path[J]. Transactions of China Electro- technical Society, 2019, 34(2): 264-274.

[8] Ayman S A, Shehab A, Ahmed M M. Steady-state equivalent circuit of five-phase induction machines with different stator connections under open-line conditions[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 4651-4662.

[9] 劉海濤, 易新強, 王東, 等. 五相感應電機缺相容錯運行的全轉矩范圍效率優化控制策略[J]. 中國電機工程學報, 2020, 40(5): 1642-1653.

Liu Haitao, Yi Xinqiang, Wang Dong, et al. Optimal efficiency control strategy in full torque range for five-phase induction motor fault tolerant operation[J]. Proceedings of the CSEE, 2020, 40(5): 1642-1653.

[10] Prasoon C M, Rajeevan P P. A space vector based PWM scheme for realization of virtual pentagon, pentacle connections in open-end winding five phase machine drives with single DC source[C]//2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 2018: 1-6.

[11] 陳超, 陳振, 趙靜, 等. 基于五相電流源型逆變器的一種新型PMSM就近空間矢量容錯組合策略[J]. 電工技術學報, 2020, 35(增刊2): 404-412.

Chen Chao, Chen Zhen, Zhao Jing, et al. A novel PMSM near space vector fault tolerant combination strategy based on five-phase current source inverter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 404-412.

[12] 劉國海, 宋成炎, 徐亮, 等. 基于SVPWM的五相永磁同步電機兩相開路故障容錯控制策略[J]. 電工技術學報, 2019, 34(1): 23-32.

Liu Guohai, Song Chengyan, Xu Liang, et al. SVPWM-based fault-tolerant control strategy under two-phase opencircuit fault of five-phase permanent- magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 23-32.

[13] Sonali C R, Hiralal M S, Bhavika S. Harmonic content testing for different stator winding con- nections of five-phase induction motor[C]//IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 2016: 1-5.

[14] Siavash S, Leila P, Hamid A T. Extending speed range of five-phase PM machines by changing the stator windings connections[C]//IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 2011: 1540-1545.

[15] Ayman S A, Ahmed M S, Shehab A, et al. Effect of stator winding connection on performance of five- phase induction machines[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 3-19.

[16] Mahmoud I M, Ayman S A, Rashid S A, et al. Effects of unbalanced voltage on the steady-state per- formance of a five-phase induction motor with three different stator winding connections[C]//International Conference on Electrical Machines (ICEM), Berlin, Germany, 2014: 1583-1589.

[17] Pavel Z. Behavior of a five-phase pentacle connected IM operated under one-phase fault[C]//International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Con- ference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 2019: 126-131.

[18] Ayman S A, Mohamed A E, Shehab A, et al. An improved fault-tolerant five-phase induction machine using a combined star/pentagon single layer stator winding connection[J]. IEEE Transactions on Indu- strial Electronics, 2016, 63(1): 618-628.

[19] Ayman S A, Shehab A, Ahmed M M, Steady-state mathematical modeling of a five-phase induction machine with a combined star/pentagon stator winding connection[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(3): 1331-1343.

[20] Ayman S A, Shehab A, Ahmed M M, Dynamic modeling of a five-phase induction machine with a combined star/pentagon stator winding connection[J]. IEEE Transactions on Energy Conversion, 2016, 31(4): 1645-1656.

（編輯 崔文靜）

Comparison and Analysis of the Performance of Five-Phase Induction Motors with Different Stator Winding Connections under Open-Circuit Conditions

（School of Electrical and Electronic Engineering Harbin University of Science and Technology Harbin 150080 China）

Based on the existing single winding and star-pentagon combined winding, this paper proposed three new types of combined windings: pentagon-star winding, pentacal-star winding, and star-pentacal winding, to study the effects of different winding connections on five-phase motors. First, the winding magnetomotive force (MMF) model and the voltage unbalance ratio measurement model were developed. The harmonic content of the motor winding MMF and the voltage unbalance ratio were calculated using the finite element method. Secondly, a 15kW five-phase induction motor was designed. Using this as a prototype, the steady-state output of a five-phase induction motor with various winding connections was investigated under open-circuit faults. According to the simulation and experimental results, the pentagon winding is most beneficial to the motor's operation for the single winding connection under open-circuit faults. Comparing with the existing star-pentagon winding for the combined winding, the pentagon-star winding introduced in this paper not only has a low MMF harmonic content, but can reduce the voltage unbalance ratio and increase the maximum load torque, which is beneficial to the motor running under open-circuit.

Five-phase motor, combined winding, open-circuit fault, max torque ratio, voltage unbalanced factor (VUF)

10.19595/j.cnki.1000-6753.tces.201643

TM343

范舒婷 女，1995年生，博士研究生，研究方向為特種電機的設計及其物理場分析。E-mail: 804296248@qq.com

孟大偉 男，1956年生，教授，博士生導師，研究方向為特種電機CAD及優化設計的理論與應用。E-mail: mengdawei@hrbust.edu.cn（通信作者）

國家自然科學基金（52077047）和黑龍江省自然基金（LH2020E092）資助項目。

2020-12-15

2021-03-02