地磁暴對電力系統穩定性的影響

王澤忠 司 遠 劉連光

地磁暴對電力系統穩定性的影響

王澤忠1司 遠1劉連光2

（1. 高電壓與電磁兼容北京市重點實驗室（華北電力大學） 北京 102206 2. 新能源電力系統國家重點實驗室（華北電力大學） 北京 102206）

鑒于近年來地磁暴侵害中低緯度地區電網事件的增加及強地磁暴引起的魁北克大停電事故，分析地磁暴對電力系統穩定運行的影響十分必要。受各種因素的約束，電力系統往往運行在極限穩定狀態，地磁暴感應電流（GIC）會引起變壓器無功損耗（以下簡稱為GIC-Q）增加，具有全網群發性和波動性的GIC-Q是否會增大系統失穩風險以及直流系統的加入是否會對電網抗磁暴能力產生影響尚未得到研究。從電力系統穩定的角度出發，研究長時間尺度下變電站GIC-Q的概率分布規律，結合GIC標準算例，在系統原有負荷的基礎上將GIC-Q作為一種無功負荷，分析地磁暴對交流系統及交直流混聯系統概率穩定性的影響。

地磁暴 GIC-Q 交直流混聯系統 電力系統穩定性 概率分布

0 引言

隨著電網規模的擴大，電壓等級的升高及大截面多分裂導線的應用，地磁感應電流（Geomagnetically Induced Currents, GIC）侵害中低緯度地區電網事件增加[1-2]，對電網安全穩定運行構成潛在威脅。地磁暴作為一種極端空間天氣災害，是一種概率事件，以某一次具體的地磁暴事件評估其對電網的影響并不能客觀反映電網抗地磁暴能力。

文獻[3]提出將GIC作為衡量電網地磁暴災害水平的指標，將地磁暴電網風險分為“低”“中”“高”和“極高”，研究地磁暴對系統的影響程度。但是GIC的大小并不能完全反映地磁暴對系統穩定造成的影響，并且魁北克大停電事故分析結果表明GIC引起變電站無功損耗（以下簡稱為GIC-Q）驟增導致無功不平衡才是事故的誘因。研究長時間尺度下GIC-Q概率分布規律需要長期、大量的地磁臺地磁場測量數據作為統計樣本。文獻[4]借助地磁臺觀測的歷史地磁暴數據對實際電網GIC進行仿真分析。文獻[5-6]依據p指數、st指數、指數篩選磁暴事件，對多次磁暴事件進行了討論。這些研究為進行多次地磁暴對電力系統穩定影響分析提供了基礎數據及地磁暴事件選擇標準。為了將地磁暴與系統穩定性耦合起來，需對多次地磁暴事件變電站大量的GIC-Q計算數據進行采樣，在原有負荷的基礎上將GIC-Q樣本作為沖擊負荷施加在系統中，因此GIC-Q概率分布特征成為關鍵。

關于地磁暴對電力系統的影響，文獻[7]將GIC-Q作為負荷施加到系統中，通過潮流計算研究節點電壓是否會低于規定水平。這種研究只是在恒功率負荷的基礎上研究節點電壓波動，一方面不能反映GIC-Q的波動性，另一方面并沒有考慮施加GIC-Q之前實際系統中大量存在的異步電動機負荷。異步電動機負荷的無功功率與端電壓的關系會進一步惡化發生地磁暴時系統的無功情況[8]。隨著特高壓電網的大規模建設及電網運行成本的限制，電力系統往往運行在穩定極限狀態。發生地磁暴時地磁場強度的不確定性使GIC-Q具有隨機性，地磁暴的全球同步性使GIC-Q具有全網群發性[9]，地磁暴引起的GIC-Q驟增作為一種沖擊性的無功波動負荷施加在系統中是否會對系統的穩定造成影響，以及直流系統的加入能否提高電力系統抗磁暴災害的能力尚未得到研究。

針對上述問題，本文從電力系統概率穩定性的角度出發，以GIC標準網絡[10]為例，利用一個太陽活動周期內強地磁暴地磁場數據計算變電站GIC-Q，得到GIC-Q的概率分布函數。利用拉丁超立方采樣獲得GIC-Q樣本，在原有負荷的基礎上，將GIC-Q作為無功負荷施加到系統中，基于概率小擾動穩定性方法研究地磁暴對系統的影響，并對比交流系統和交直流混聯系統抗地磁暴災害能力的強弱，為電網磁暴風險評估和有針對性地設計防治措施提供依據。

1 GIC-Q計算

1.1 感應地電場計算

關于有限元法計算地磁暴感應地電場，本文不再贅述基本方程，只說明邊界條件。不考慮地球曲率的影響，使用直角坐標系，軸的正向為北，軸正向為東，軸正向垂直地面向下，利用大地電磁測深數據建立大地電導率模型[11]。地面邊界條件為

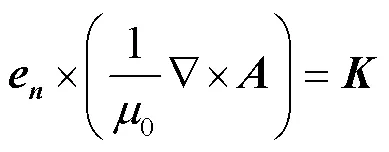
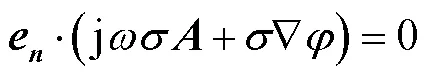
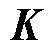
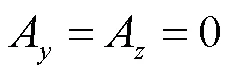
1.2 GIC計算

根據每條線路兩端變電站的經緯度坐標，對線路做分段處理，即將線路平均分為段，得到每個線段中點的地理坐標，尋找每條線段中點對應的地磁擾動（Geomagnetic Disturbance, GMD）地電場強度。在電網GIC的模型中將等效電壓源的積分公式[12]簡化為

基于場路理論，GIC的計算方法為[10]

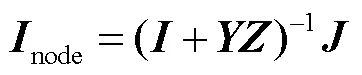
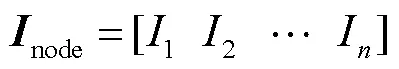
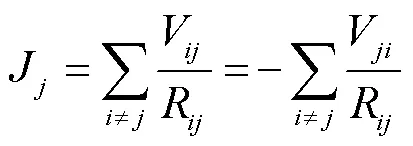
1.3 基于K值的GIC-Q算法

GIC作為一種準直流電流流經變壓器繞組時產生半波飽和效應，導致變壓器無功損耗增加。本文將由GIC引起的大量變壓器無功損耗增量稱為電網群發GIC無功擾動[13]，且其與GIC大小近似呈線性關系。不同鐵心結構的變壓器在同樣GIC水平下的無功損耗不同，對應的比例系數值不同。除此之外，運行電壓也對變壓器的GIC無功損耗產生影響，變壓器GIC-Q模型為

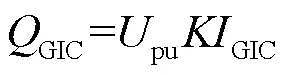
在大規模電網的GIC-Q損耗研究中會涉及不同電壓等級的變壓器，對同一鐵心類型但不同運行電壓的變壓器，其GIC-Q損耗模型需對式（6）進行修改為[14]

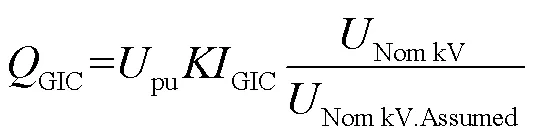
2 GIC-Q樣本獲取

2.1 地磁暴事件選取

本文將第24個太陽活動周期內st指數≤-100nT的地磁暴事件作為典型案例[15]，研究地磁暴對電力系統穩定性的影響。結合新疆地區大地電導率數據，搭建三維大地電導率模型，如圖1所示。將GIC標準網絡中變電站的經緯度坐標調整到37°N～45°N、75°E～96°E范圍內，使變電站均位于大地電導率模型范圍內。

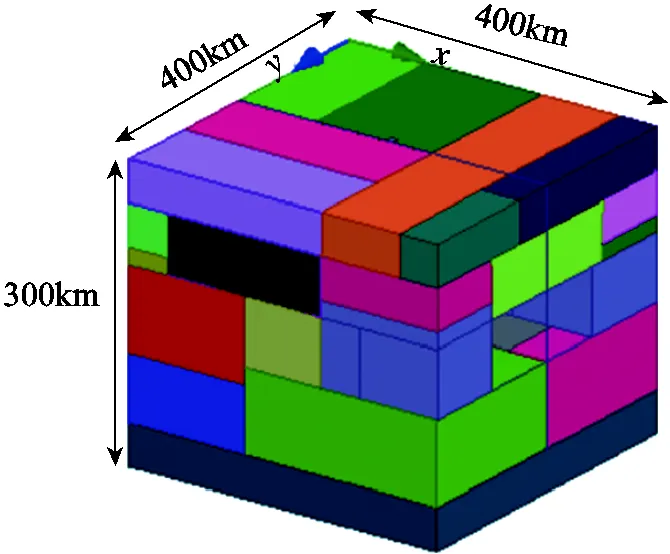
圖1 三維大地電導率模型

GIC標準網絡如圖3所示，系統中的負荷為沒有發生地磁暴時的基礎負荷。根據1.2節GIC計算方法，將GIC標準網絡中各條線路平均分為10段，根據線路首末端的經緯度坐標得到各個線段的中點坐標，再由線段的中點坐標查找對應的GMD地電場，根據式（3）將地面感應電場等效成網絡中的電源，建立基于線路感應電壓源的電網GIC等效網絡，由導納矩陣法計算得到電網的GIC。

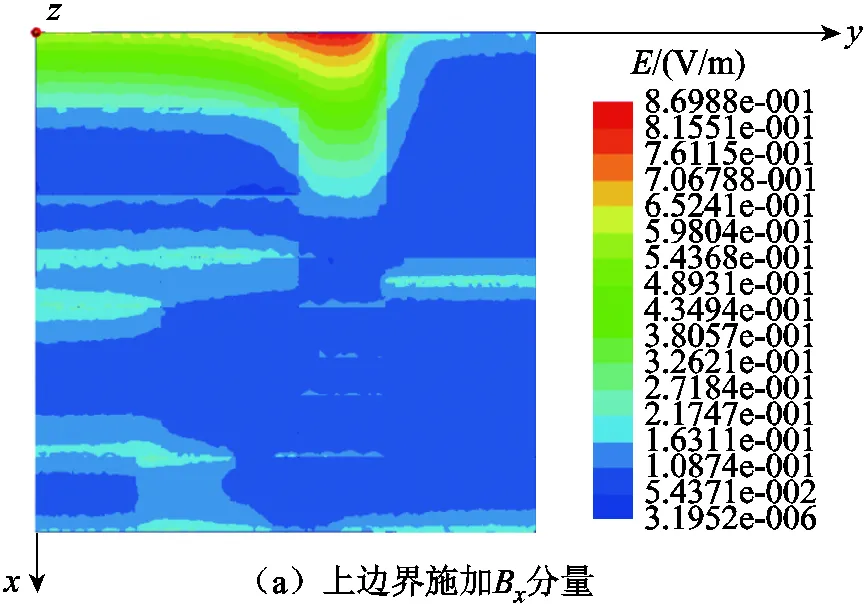
圖3 GIC標準網絡模型接線圖

2.2 GIC-Q概率分布

基于GIC標準網絡計算第24個太陽活動周期內強地磁暴事件中各變電站的GIC-Q，本文選取正態分布、伽瑪分布、瑞利分布、指數分布及韋伯分布對各個變電站GIC-Q數據分別進行擬合，得到不同分布的可決系數[15]，利用可決系數判定韋伯分布模型擬合各變電站GIC-Q效果最好。各個變電站GIC-Q擬合得到的比例參數和形狀參數見表1。

未發生地磁暴時，對符合正態分布的有功、無功基礎負荷進行拉丁超立方采樣得到1 000組基礎負荷樣本。對于一個太陽活動周期的強地磁暴事件中SUB2、SUB3、SUB4、SUB5、SUB6、SUB8的GIC-Q同樣進行拉丁超立方采樣，得到1 000組GIC-Q樣本作為無功負荷施加到節點17、16、4、5、6、12。

表1 各變電站GIC-Q概率分布參數

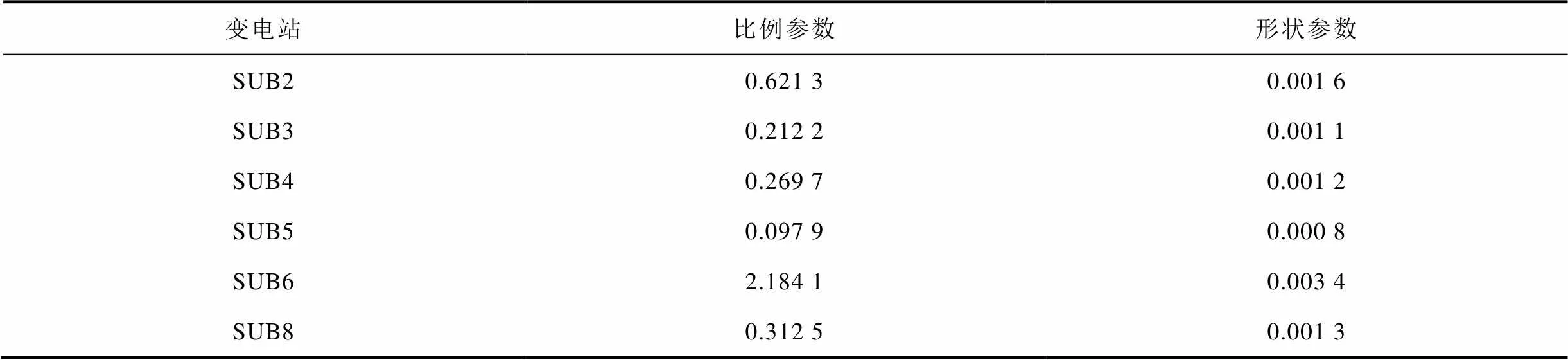
Tab.1 GIC-Q probability distribution parameters of each substation

3 地磁暴對系統穩定性影響分析

3.1 地磁暴引起系統失穩風險指標

考慮到除1989年地磁暴導致加拿大魁北大停電外，其余地磁暴事件并未使系統的網絡拓撲結構發生變化。GIC作為一種準直流電流，將導致變壓器半波飽和，半波飽和狀態的變壓器可以被看作電網的一個無功負荷。GIC引起的變壓器無功擾動具有全網群發性，導致系統的GIC-Q總量較大。為了將地磁暴同電力系統穩定性結合起來，將地磁暴引起的變電站GIC-Q作為一種無功負荷波動施加到系統中，研究地磁暴對電力系統小擾動穩定性的影響。由于GMD地磁場強度的隨機性會造成GIC-Q的不確定，采用概率分析法結合系統失穩概率和風險指標研究地磁暴對系統穩定性的影響。此外，考慮到實際系統中大部分負荷為異步電動機負荷，所以將原有基礎負荷、GIC-Q和異步電動機負荷同時施加到節點上，通過分析統計學特征研究地磁暴對系統穩定性的影響。

1）以狀態矩陣出現正實部特征根作為失穩判據，則地磁暴引起系統失穩概率為

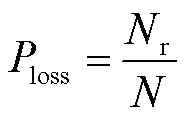
2）考慮可能會存在特征根的實部集中在臨界失穩區間內，僅以式（8）失穩指標評價失穩風險不夠客觀，引入振蕩失穩危險系數[16]，并建立地磁暴引起系統概率失穩風險評價指標為

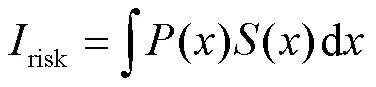
3.2 地磁暴對交流系統穩定性影響分析

GIC標準網絡系統基準容量為100MV·A，頻率為50Hz，系統參數如下：

1）同步發電機：額定功率為1 000MW，額定電壓為20kV。G1:1=1.03(pu)∠6.8°，平衡節點；G2:2=700MW，2=200Mvar，PQ節點；G3:3=700MW，3=1.03(pu)，PV節點；G4:4=700MW，4=1.01(pu)，PV節點；G5:5=700MW，5=300Mvar，PQ節點；G6:6=700MW，6=300Mvar，PQ節點；G7:7=700MW，7=300Mvar，PQ節點。

同步發電機采用四階模型，勵磁系統采用三階模型，調速器采用二階模型，感應電動機采用三階負荷模型。為減小系統狀態變量數量，并更好地展示系統的振蕩模式，系統中同步發電機均未裝設電力系統靜態穩定器。

2）負荷：節點16、15、4、6、5的有功負荷分別服從期望值為500MW、1 200MW、500MW、300MW、1 200MW，標準差為期望值0.1倍的正態分布；無功功率分別服從期望值為200Mvar、500Mvar、600Mvar、150Mvar、350Mvar，標準差為期望值0.1倍的正態分布。對19次地磁暴事件中SUB2、SUB3、SUB4、SUB5、SUB6、SUB8的GIC-Q進行采樣，得到1 000組GIC-Q樣本作為無功負荷施加到節點17、16、4、5、6、12。同時在進行小擾動穩定分析時，在節點16、15、4、6、5施加異步電動機負荷，異步電動機慣性時間常數為2.0，定子電阻為0.02(pu)，定子電抗為0.18(pu)，勵磁電抗為0.35(pu)，轉子電阻為0.02(pu)，轉子電抗為0.12(pu)，轉矩方程常數為0.85。

將全系統的微分方程組進行線性化處理，求解狀態矩陣的特征根，結合系統概率穩定性指標確定地磁暴對電力系統穩定的影響。仿真計算GIC標準算例的特征根，研究發生地磁暴時系統的概率穩定性。根據機電相關比確定三個關鍵振蕩模式，其中兩個區內局部振蕩模態，一個區域間振蕩模態。振蕩模式1發生在區域3內部，與機組G5、G6強相關，模式2發生在區域1內部，與機組G2、G3強相關，模式3發生在區域1和區域3之間，與機組G3、G4、G6強相關。特征根在復平面分布情況如圖4所示，其中橫軸為特征根實部，縱軸為特征根虛部，實線和虛線分別為阻尼比為0.05、0.01的等阻尼比線。

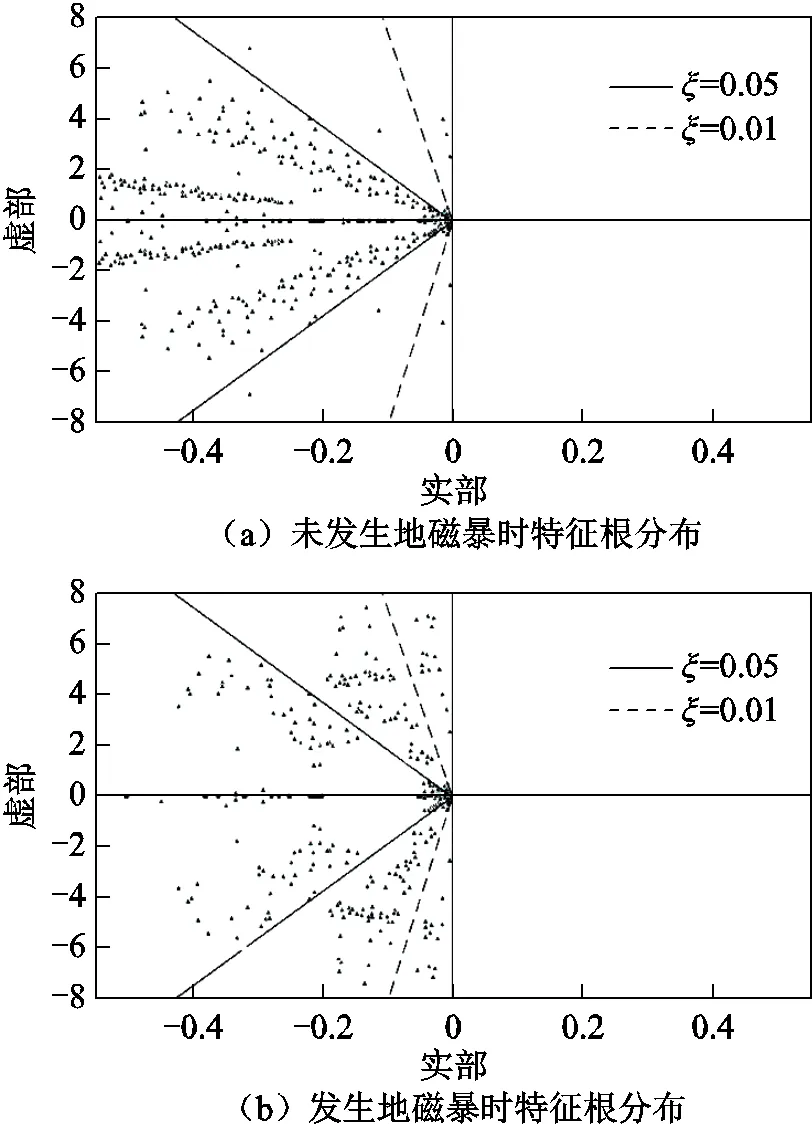
圖4 特征根分布

由圖4可知，地磁暴對系統特征根的分布產生影響。未發生地磁暴時特征根集中分布在阻尼比為0.05的區域內；發生地磁暴時，特征根開始向阻尼比較小的區域內移動。交流系統特征根統計結果見表2。

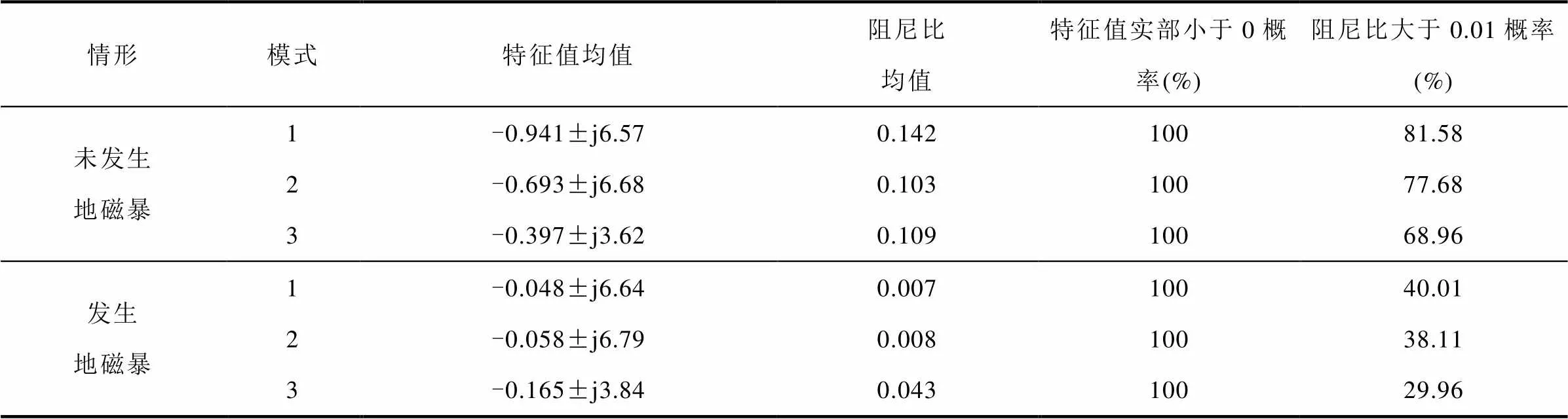
表2 交流系統特征根統計結果

由表2的數據可知，對于特征值，相比于未發生地磁暴的情況，無論是區內振蕩模式還區間振蕩模式，雖然特征根實部均小于零，但阻尼比大于0.01的概率及阻尼比均值都有所下降。當發生地磁暴時，區內振蕩模式1阻尼比下降95.07%，阻尼比大于0.01的概率下降50.96%；區內振蕩模式2阻尼比下降92.23%，阻尼比大于0.01的概率下降50.94%；區間振蕩模式3阻尼比下降60.55%，阻尼比大于0.01的概率下降56.55%。

為比較拉丁超立方采樣和簡單隨機采樣的結果，利用簡單隨機采樣得到10 000組基礎負荷樣本和10 000組GIC-Q樣本，將其施加在同樣的節點上計算特征根，其中區間振蕩模式1特征根實部的概率密度函數（Probability Density Function, PDF）和累積分布函數（Cumulative Distribution Function, CDF）如圖5所示。

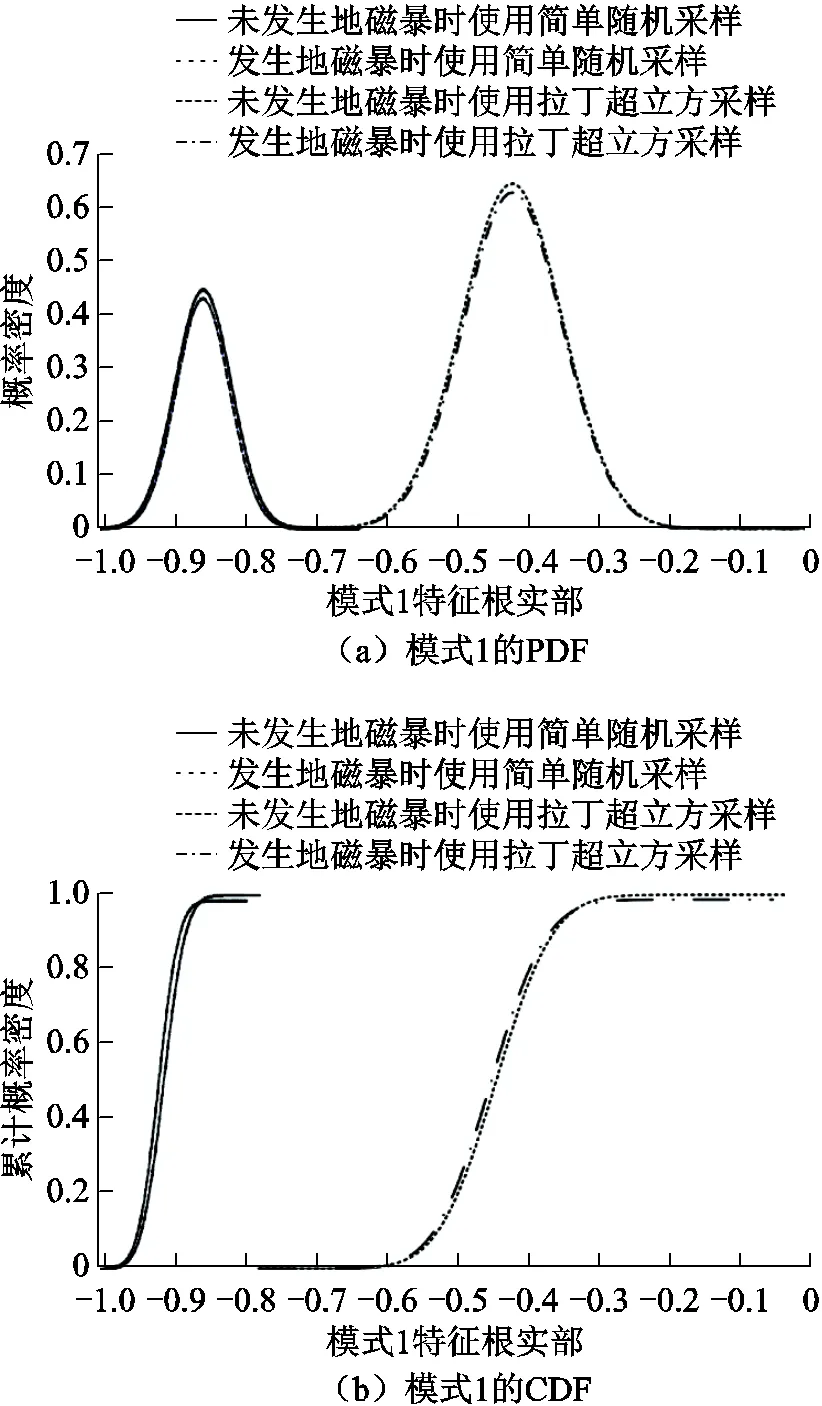
圖5 模式1特征根的PDF和CDF

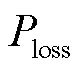
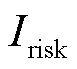
表3 交流系統失穩風險指標值

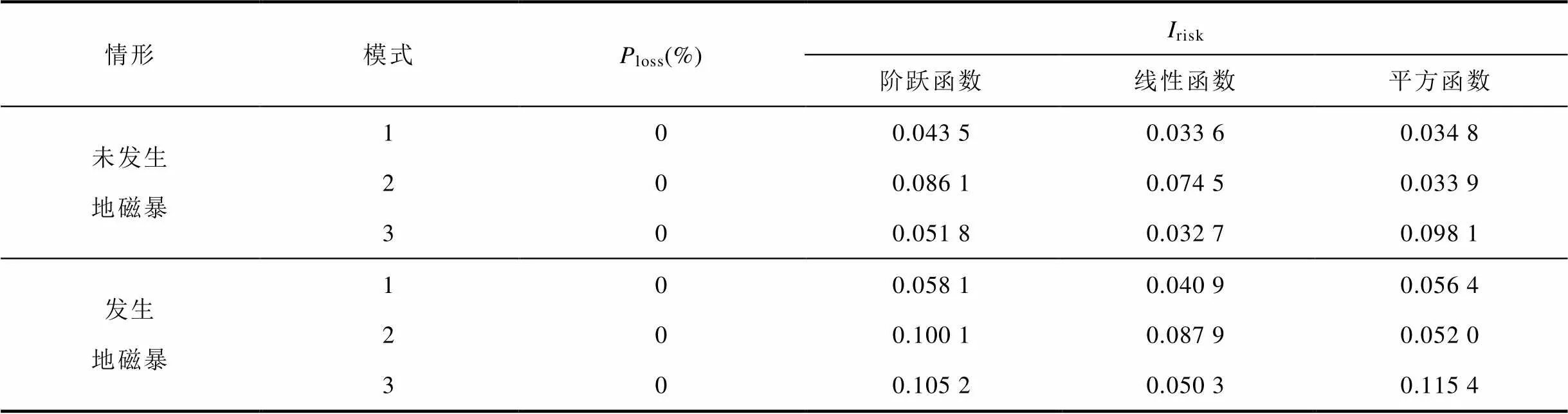
Tab.3 AC system instability risk index value

3.3 交流系統和交直流混聯系統對比

為了研究直流系統的加入對系統抗磁暴災害能力的影響，將GIC標準算例的線路15-6中的一條改為直流線路，靠近節點15為逆變站，靠近節點6為整流站，HVDC數學模型采用準穩態模型[17]。對于直流系統，逆變側和整流側換流變壓器的等效電抗分別為0.033 6、0.033 6；直流輸電線路電阻、電抗分別為0.010 3、0.025；直流參考電流為1.3；控制系統時間常數、比例系數為0.05、1；逆變側和整流側換流變壓器電壓比為1、1；觸發延遲角和熄弧超前角分別為18°、20°，整流側和逆變側均有125Mvar的無功支撐，其他元件參數及采樣規模與交流系統一致。交直流混聯系統的特征根統計結果見表4。

表4 交直流混聯系統特征根統計結果

Tab.4 Statistical results of characteristic roots of AC/DC hybrid system

對比發生磁暴時表2和表4的統計數據可知：未發生地磁暴時，直流系統的加入使區內振蕩模式1阻尼比大于0.01的概率增加9.24%，阻尼比均值增加15.49%，區內振蕩模式2阻尼比大于0.01的概率增加3.62%，阻尼比均值增加7.76%，區間振蕩模式3阻尼比大于0.01的概率減小12.87%，阻尼比均值減小6.42%。發生地磁暴時，相比于未發生地磁暴時，交直流系統無論是區內振蕩模式還是區間振蕩模式，阻尼比大于0.01的概率及阻尼比均值都有所下降。區內振蕩模式1阻尼比大于0.01的概率下降49.36%，阻尼比均值下降73.78%；區內振蕩模式2阻尼比大于0.01的概率下降43.93%，阻尼比均值下降43.24%；區間振蕩模式3阻尼比大于0.01的概率下降70.02%，阻尼比均值下降75.49%。發生地磁暴時，相比于交流系統，交直流混聯系統區內振蕩模式1阻尼比大于0.01的概率增加12.79%，阻尼比均值增加514.28%，區內振蕩模式2阻尼比大于0.01的概率增加13.85%，阻尼比均值增加87.3%。因此，直流系統的加入在一定程度上改善了系統的區內振蕩阻尼特性。而直流系統的加入使區間振蕩模式阻尼比大于0.01的概率下降39.80%，阻尼比均值下降41.86%，惡化了區間振蕩模式。無論是交流系統還是交直流混聯系統，區內振蕩模式阻尼比大于0.01的概率只有40%左右，區間振蕩模式大于0.01的概率只有20%左右，發生磁暴時將難以滿足系統穩定要求。對于交直流混聯系統，同樣采用三種不同形式的振蕩失穩危險函數計算振蕩模式1在未發生地磁暴時及發生地磁暴時三種振蕩模式下的小擾動概率穩定風險指標，結果見表5。

表5 交直流混聯系統失穩風險指標值

Tab.5 Instability risk index value of AC/DC hybrid system

對比交直流混聯系統和交流系統，當未發生地磁暴且振蕩失穩函數取階躍函數時，區內振蕩模式1、2及區間振蕩模式3的概率失穩指標值分別下降25.06%、27.76%、20.46%；當振蕩失穩函數取線性函數時，區內振蕩模式1、2及區間振蕩模式3的概率失穩指標值分別下降47.02%、44.69%、43.73%；當振蕩失穩函數取平方函數時，區內振蕩模式1、2及區間振蕩模式3的概率失穩指標值分別下降66.95%、69.91%、32.93%。對于交直流混聯系統，當發生地磁暴且振蕩失穩函數取階躍函數時，區內振蕩模式1、2及區間振蕩模式3的概率失穩指標值分別上升12.58%、18.00%、28.88%；當振蕩失穩函數取線性函數時，區內振蕩模式1、2及區間振蕩模式3的概率失穩指標值分別上升35.39%、32.52%、44.57%；當振蕩失穩函數取平方函數時，區內振蕩模式1、2及區間振蕩模式3的概率失穩指標值分別上升65.26%、33.33%、55.17%。發生地磁暴時，比較交流系統和交直流混聯系統的失穩指標值：對于區內振蕩模式1，當振蕩失穩函數分別取階躍函數、線性函數和平方函數時，失穩指標值分別下降36.83%、41.07%、41.31%；對于區內振蕩模式2，當振蕩失穩函數分別取階躍函數、線性函數和平方函數時，失穩指標值分別下降26.67%、37.88、70.57%；對于區間振蕩模式3，當振蕩失穩函數分別取階躍函數、線性函數和平方函數時，失穩指標值分別下降49.52%、47.11%、11.52%。直流系統的加入雖然沒有使loss增加，但相比于未發生地磁暴時無論交流系統還是交直流混聯系統，地磁暴均使系統區內振蕩和區間振蕩失穩風險增加。相比于交流系統，直流系統的加入使區內振蕩失穩風險指標值降低，但使區間振蕩失穩風險指標值增加。因此，對于交直流混聯系統更應關注地磁暴對區間振蕩失穩的影響。

4 結論

本文以GIC標準網絡為例，仿真計算了一個太陽活動周期多次強地磁暴擾動下的各個變電站的GIC-Q，給出GIC -Q的概率密度分布函數，利用拉丁超立方采樣獲得GIC-Q樣本，在原有負荷的基礎施加GIC-Q和異步電動機負荷，研究地磁暴對交流系統和交直流混聯系統穩定性的影響，主要結論如下：

1）各個變電站的GIC-Q概率分布模型符合韋伯分布。從系統穩定性的角度出發，將具有全網群發性和波動性的GIC-Q作為一種小擾動施加到系統中，并基于振蕩失穩函數提出地磁暴對電力系統穩定性影響概率評價指標。研究發現，發生地磁暴時系統的特征根分布向阻尼比小的區域移動，系統失穩概率增加。

2）結合目前普遍存在的交直流混聯系統，在研究地磁暴對系統穩定性的影響時考慮直流系統的影響，研究發現：直流輸電系統的加入在一定程度上改善了發生地磁暴時系統的區內振蕩阻尼特性，但同時也惡化了區間振蕩。因此，對于交直流混聯系統更應重視發生地磁暴時可能引起電力系統區間振蕩失穩的潛在威脅。

3）以GIC標準系統為例，研究地磁暴對電力系統穩定性影響的規律和判據，根據系統小干擾穩定性計算結果建立風險評估指標，將系統小干擾失穩風險進行量化，以期在考慮小干擾穩定阻尼比等約束條件下建立以系統成本、發電調整量及小干擾穩定性風險最小為目標的多目標優化函數，進行地磁暴災害防治。

[1] Blake S P, Gallagher P T, McCauley J, et al. Geomagnetically induced currents in Irish power network during geomagnetic storms[J]. Space Weather, 2016, 14(12): 1136-1154.

[2] 黃天超, 王澤忠. 地磁暴對直流輸電逆變側換相角及諧波的影響機理分析[J]. 電工技術學報, 2020, 35(16): 3377-3384.

Huang Tianchao, Wang Zezhong. Mechanism analysis of geomagnetic storm on commutation angle and harmonic of invert side of HVDC transmission[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3377-3384.

[3] Marshall R A, Smith E A, Francis M J, et al. A preliminary risk assessment of Australian region power network to space weather[J]. Space Weather, 2011, 9(10): 1-18.

[4] 劉春明. 中低緯電網地磁感應電流及其評估方法研究[D]. 北京: 華北電力大學, 2009.

[5] Barbosa C, Alves L, Caraballo R, et al. Analysis of geomagnetically induced currents at a low-latitude region over the solar cycles 23 and 24: comparison between measurements and calculations[J]. Journal of Space Weather and Space Climate, 2015, 5: A35．

[6] Blake S P, Gallagher P T, McCauley J, et al. Geomagnetically induced currents in the Irish power network during geomagnetic storms[J]. Space Weather, 2016, 14(12): 1136-1154．

[7] 楊培宏, 劉連光, 劉春明, 等. 地磁暴引起電網電壓波動抑制策略[J]. 高電壓技術, 2017, 43(5): 1707-1714.

Yang Peihong, Liu Lianguang, Liu Chunming, et al. Strategy for restraining voltage fluctuation in power network caused by geomagnetic storm[J]. High Voltage Engineering, 2017, 43(5): 1707-1714．

[8] 廖衛平, 張艷, 馮佳偉, 等. 考慮不對稱故障影響的感應電動機負荷動態特性快速解析算法[J]. 電工技術學報, 2020, 35(19): 4183-4193.

Liao Weiping, Zhang Yan, Feng Jiawei, et al. Fast analytical method for calculating the dynamic performance of induction-motor loads considering the effect of asymmetrical fault[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4183-4193.

[9] 王澤忠, 黃天超. 特高壓變壓器地磁感應電流和無功功率關系的定量分析[J]. 電工技術學報, 2020, 35(22): 4709-4716.

Wang Zezhong, Huang Tianchao. Quantitative analysis of geomagnetically induced current-Q relation of UHV transformer[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4709-4716.

[10] Horton R, Boteler D, Overbye T J, et al. A test case for the calculation of geomagnetically induced current[J]. IEEE Transaction Power Delivery, 2012, 27(4): 2368-2373.

[11] 王澤忠, 董博, 劉春明, 等. 華北地區大地電性結構三維建模及磁暴感應地電場有限元計算[J]. 電工技術學報, 2015, 30(3): 61-66.

Wang Zezhong, Dong Bo, Liu Chunming, et al. Three-dimensional earth conductivity structure modeling in north China and calculation of geoelectromagnetic fields during geomagnetic disturbances based on finite element method[J]. Transactions of China Electrote-chnical Society, 2015, 30(3): 61-66.

[12] 劉連光, 郭世曉, 魏愷, 等. 基于全節點模型的三華電網地磁感應電流計算[J]. 電網技術, 2014, 38(7): 1946-1952.

Liu Lianguang, Guo Shixiao, Wei Kai, et al. Calculation of geomagnetically induced currents in interconnected north China-central China-east China power grid based on full-node GIC model [J]. Power System Technology, 2014, 38(7): 1946-1952.

[13] 李冰, 王澤忠, 劉恪, 等. 特高壓變壓器直流偏磁對繞組電流的影響[J]. 電工技術學報, 2020, 35(7): 1422-1431.

Li Bing, Wang Zezhong, Liu Ke, et al. Research on winding current of UHV transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1422-1431.

[14] 劉連光, 朱溪, 王澤忠, 等. 基于K值法的單相四柱式特高壓主體變的GIC-Q損耗計算[J]. 高電壓技術, 2017, 43(7):2 340-2348.

Liu Lianguang, Zhu Xi, Wang Zezhong, et al. Calculation for reactive power loss of single-phase four limbs UHV transformer due to geomagnetically induced current with parameter K[J]. High Voltage Engineering, 2017, 43(7): 2340-2348.

[15] 劉春明, 王紅梅, 王璇. 多次磁暴下特高壓電網GIC統計規律研究[J]. 中國電機工程學報, 2019, 39(15): 4606-4615.

Liu Chunming, Wang Hongmei, Wang Xuan. Statistical analysis of geomagnetically induced current in UHV power grids under multiple geomagnetic storms[J]. Proceedings of the CSEE, 2019, 39(15): 4606-4615.

[16] 劉佳. 大規模風電接入的電力系統小干擾穩定及控制方法研究[D]. 北京: 華北電力大學, 2019.

[17] 鄭安然, 郭春義, 殷子寒, 等. 提高弱交流系統下混合多端直流輸電系統小干擾穩定性的控制參數優化調節方法[J]. 電工技術學報, 2020, 35(6): 1336-1345.

Zheng Anran, Guo Chunyi, Yin Zihan, et al. optimal adjustment method of control parameters for improving small-signal stability of hybrid multi-terminal HVDC system under weak AC condition[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1336-1345.

Influence of Geomagnetic Storms on the Stability of Power System

Wang Zezhong1Si Yuan1Liu Lianguang2

（1. Beijing Key Laboratory of High Voltage and EMC North China Electric Power University Beijing 102206 China 2. State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China）

In view of the increase of geomagnetic storms invading the power grid in middle and low latitudes in recent years and the blackout accident in Quebec caused by strong geomagnetic storm, it is necessary to analyze the impact of geomagnetic storms on the stable operation of power system. Constrained by various factors, the power system often operates in a state of extreme stability. The geomagnetically induced current (GIC) causes an increase in the reactive power loss (GIC-Q) of the transformer. Whether the GIC-Q with the whole network clustering and volatility will increase the risk of system instability and whether the addition of the DC system will affect the anti-geomagnetic storm ability of the power grid has not been studied. From the perspective of power system stability, the probability distribution law of substation GIC-Q in long time scale is studied. Combined with the GIC benchmark network model, GIC-Q is added to the system on the basis of the original load, and the influence of geomagnetic storm on the probability stability of AC system and AC/DC hybrid system is analyzed.

Geomagnetic storms, geomagnetically induced current-Q(GIC-Q), AC/DC hybrid system, power system stability, probability distribution

10.19595/j.cnki.1000-6753.tces.210086

TM712

王澤忠 男，1960年生，博士，教授，博士生導師，研究方向為電力系統電磁兼容和電磁場數值計算。E-mail：wzzh@ncepu.edu.cn

司 遠 男，1993年生，博士研究生，研究方向為電網安全運行與災變控制。E-mail：siy@ncepu.edu.cn（通信作者）

2021-01-17

2021-03-08

（編輯 赫蕾）