不同支撐方式對推力軸承性能影響研究

董衛(wèi)紅， 曹寒， 陳丹， 馬駿

（東方電氣集團東方汽輪機有限公司， 四川 德陽， 618000）

1 前言

流體動壓推力軸承由于其具有摩擦功耗小，承載能力大， 運轉平穩(wěn)等優(yōu)點， 從而被廣泛應用在軸向承載的各種回轉設備中。 目前， 推力軸承廣泛采用的結構有3 種： 固定瓦推力軸承和點、線支承可傾瓦推力軸承、 點支承可傾瓦推力軸承。3 種軸承在工程上的使用效果即使同一種機組不同臺份同一個軸承都不一樣。 因此有必要對不同支撐方式對推力軸承性能影響研究。

2 不同支撐方式對推力軸承性能影響的理論分析

2.1 推力軸承分析模型的基本方程

推力軸承分析模型的基本方程為二維雷諾方程， 其基本假設： （a）潤滑油不可壓縮， 且為牛頓流體， （b）潤滑油流動為穩(wěn)態(tài)的層流流動且無滑移，（c）徹體力和慣性力忽略不計， （d）因輕載不考慮瓦的彈形變形和熱變形， （e）沿油膜厚度方向上恒溫恒壓，（f）除黏度外流體的其他物性參數(shù)為常量。 在上述假設下， 普通形式的油膜穩(wěn)態(tài)壓力方程為

式中： p 為油膜壓力； μ 為潤滑油動力黏度； Ω 為轉子角速度。

（τ1： 為油膜破裂邊界； τ： 油膜周圍邊界）

Reynolds 方程是一個二階微分方程， 通常情況下沒有解析解。 為了揭示流體潤滑的基本規(guī)律，通常可將二維流體潤滑問題簡化為一維問題， 如假設軸承為無限寬， 因而不存在寬度方向上的流動， 即此時， 雷諾方程化為一維方程， 這就是所謂的無限寬理論。 把二維問題處理成一維問題雖然不可避免會引起計算誤差， 但由于一維問題的解通常是解析的， 因而對于復雜問題往往能夠方便地給出近似的定量估計， 所以上述一維理論從某種意義上說仍具有重要意義， 其計算結果在一定工況和參數(shù)范圍內也仍具有實際工程應用價值[1]。

2.2 固定瓦推力軸承一維分析

固定瓦推力軸承由平面和一段斜面聯(lián)合組成，是工程中常見的軸承形式， 參數(shù)意義見圖1。

圖1 固定瓦推力軸承參數(shù)示意圖

其油膜厚度函數(shù)為：

由于p 僅是h 的函數(shù)， 所以p 在階梯處是連續(xù)可導的。

軸承的承載能力：

如L2=0 則h0表示了一普通斜面軸承最大壓力點處的油膜厚度， 如 L2＞0， h0值比斜面軸承小，表明壓力點向流出方向偏移， 但由于h0＞h2， 所以最大壓力點將總是位于周長的傾斜部分。 組合軸承的承載能力當L1／L2=5 時最佳， 此時軸承的承載能力將比相當面積的斜面軸承高出25%左右， 但此時由于最小膜厚所在區(qū)域較長， 導致斜平面軸承的摩擦損失較大。

在斜面軸承中，值隨運動條件而變化。

最大壓力處的膜厚：

軸承承載能力：

最大壓力處的膜厚h0=1.37h2。 軸承承載能力系數(shù)和摩擦阻力系數(shù)與傾斜參數(shù)a的關系見圖2。

圖2 軸承承載能力系數(shù)和摩擦阻力系數(shù)與傾斜參數(shù)a的關系

由于運行工況變化時a隨載荷增大而減小，會使最小膜厚減小， 可能造成潤滑失效， 但事實并非如此， 推力軸承工程中常用的比壓＜3.5 MPa，在此范圍內a不會偏離最佳值太遠， 而且摩擦阻力隨著a值的增大在減小， 使油膜溫度低， 潤滑油粘度對溫度極其敏感， 因此在工程中常用的比壓范圍內當并不會造成軸承承載能力明顯差別。

2.3 可傾瓦推力軸承一維分析

可傾瓦推力軸承的瓦塊支撐在支點上并可自由傾斜， 軸承性能計算可以按照斜面軸承同樣的方法進行， 唯一不同的是可傾瓦軸承各瓦的油膜合力在穩(wěn)態(tài)時必須通過支點， 而支點的位置在斜面軸承計算時所得到的壓力中心x*重合， 每一x*都對應于一個最小膜厚h2， 由于斜面軸承的壓力分布不對稱于L/2， 油膜合力總是偏離幾何中心的， 為了使可傾瓦軸承具有一定的承載能力， 起止點位置x*必須在大于L/2 處， 1957 年， Wilcock和Booges 推薦的x*/L=0.58。 當支點位置給定時，可由式（13）求解傾斜參數(shù)a， 進而根據(jù)式（12）求出承載能力W。 對于可傾瓦軸承， 承載能力系數(shù)、摩擦阻力系數(shù)可分別寫為：

可傾瓦軸承， 承載能力系數(shù)、 摩擦阻力系數(shù)與偏支系數(shù)的關系見圖3， 曲線表明X*/L 越大越好，這與文獻[1]中結論有區(qū)別，需后續(xù)進一步研究。

圖3 可傾瓦軸承承載能力系數(shù)、 摩擦阻力系數(shù)與偏支系數(shù)的關系

在實際運行中， 由于流體經(jīng)過軸承時會產(chǎn)生溫升而使黏度發(fā)生變化形成油膜， 同時瓦塊的熱變形和彈性變形也有助于形成潤滑膜， 這些因素使得可傾瓦會走出在支點位置位于幾何中心時也能形成一定承載能力。

2.4 一維分析結論

從一維分析可得到， 軸承性能因素受結構參數(shù)影響， 固定瓦軸承性能對坡高敏感， 可傾瓦軸承性能對支點位置敏感， 但在設計范圍內可傾瓦和固定瓦軸承的承載力系數(shù)及摩擦阻力系數(shù)范圍一致， 因此作者認為在參數(shù)設計合理的情況下，在常規(guī)的設計比壓范圍（＜3.5 MPa）內， 2 種軸承支撐方式不同是不會造成軸承性能的不一致。

2.5 不同支撐方式下軸承性能的二維分析

2.5.1 軸承矩平衡方程

固定瓦軸承二維分析僅雷諾方程， 可傾瓦軸承的二維分析還需力矩平衡方程。

理論上， 瓦塊在液膜驅動力矩作用下可以繞支點沿任意方向傾斜。 瓦塊受力平衡時， 液膜壓力的合力穿過瓦塊支點， 驅動力矩為零， 稱此時液膜合力與瓦面的交點（rb，θb）為靜力平衡點。 如不計軸向距離， 靜力平衡點位置與支點位置（rz，θz）重合， 如圖4 所示。

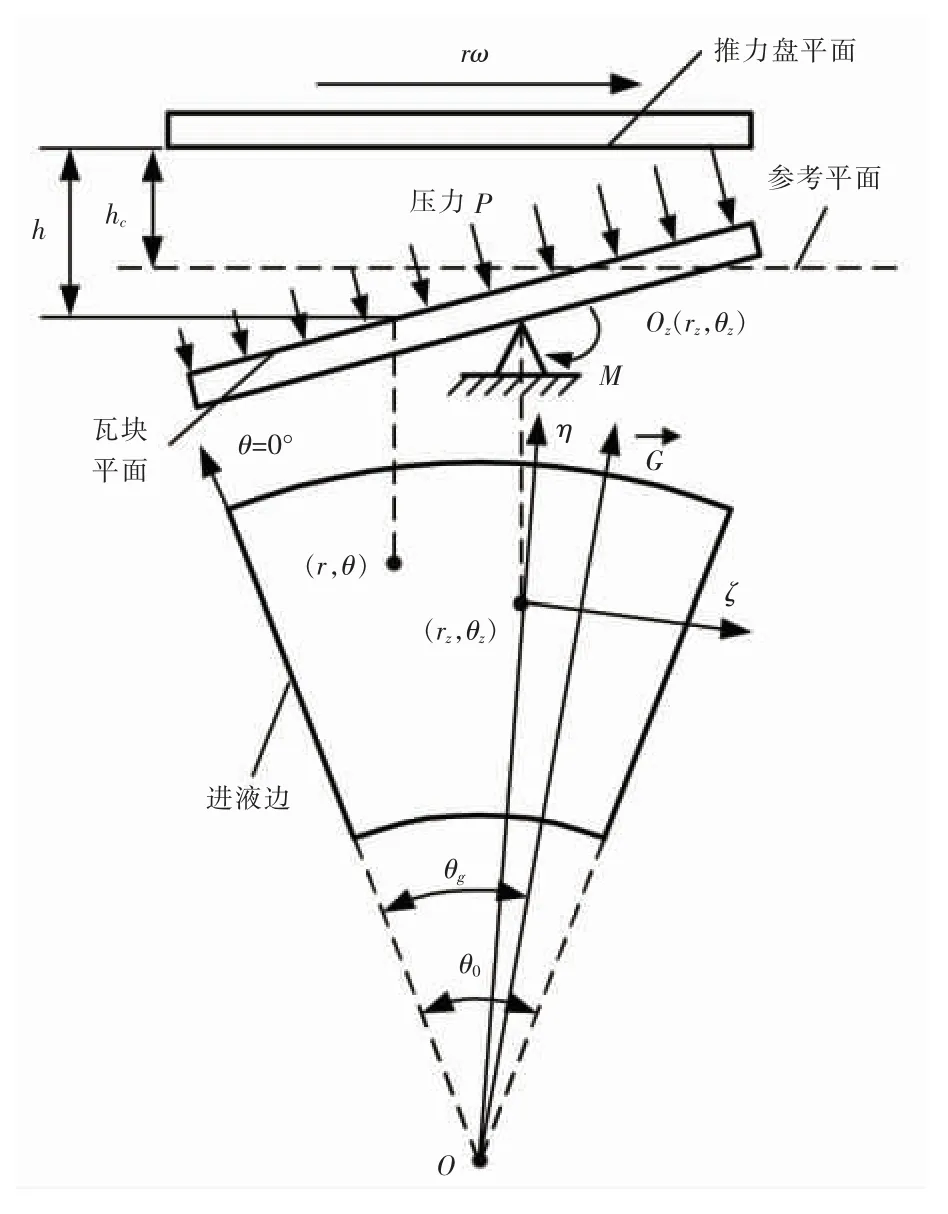
圖4 可傾瓦平衡狀態(tài)位置及受力示意圖

取一參考平面與推力盤平面平行， 相距hc，該參考平面與瓦塊平面的交線 （或交線的平行線）為線過瓦塊圓心O（或平移過圓心），線與進液邊夾角為θg（稱為交線位置角）， 定義線從進液邊開始繞O 點順時針旋轉得到的θg為正， 逆時針為負， 則取值范圍是 （-π～π）。 如圖 5 所示，γg為瓦繞線的轉動角（稱為瓦傾斜角， 無量綱用Gg表示）。 瓦的平衡狀態(tài)可用力矩平衡方程來描述， 無量綱形式為：

2.5.2 可傾瓦推力軸承動壓液膜收斂條件

如圖5 所示， 不計潤滑液在瓦內外測的泄漏，潤滑液沿虛線AB 流動。 在推力盤與瓦塊間形成收斂間隙是可傾瓦推力軸承具有動壓承載能力的一個基本條件， 該條件對瓦塊擺角取值提出了約束。令形成收斂液膜間隙的情況有： （1）當 θ2≤θg≤θ3時， 形成全收斂間隙； （2） 當 θ1＜θg＜θ2時， 形成局部收斂間隙， 其中在瓦面形成發(fā)散間隙； （3）當θ3＜θg＜θ4時 ， 形成 局部收 斂間隙， 其中 在 瓦面形成發(fā)散間隙。 潤滑模型求解時， 需要首先判斷θg取值屬于哪個區(qū)間， 從而確定最小膜厚位置。

圖5 交線位置角θg 的取值范圍

2.5.3 軸承基本參數(shù)

軸承基本參數(shù)選取按照文獻[2]， 見表1。

表1 軸承基本參數(shù)表

2.5.4 不同支撐方式軸承靜態(tài)性能參數(shù)比較及分析

不同比壓下不同支撐方式軸承靜態(tài)參數(shù)比較如圖6 所示。

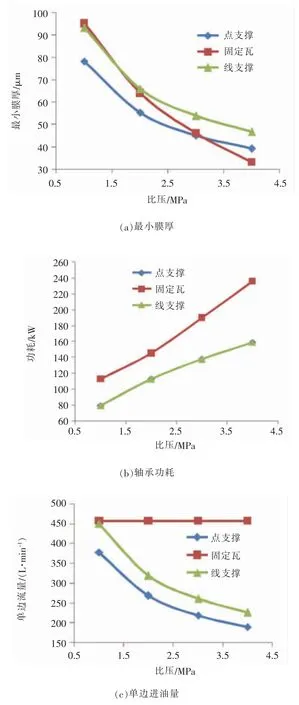
圖6 不同比壓下不同支撐方式軸承靜態(tài)參數(shù)比較圖

同尺寸推力軸承， 不同支撐方式下軸承性能相近。 性能參數(shù)不同是因為瓦塊設計參數(shù)不同造成的。 線支撐及點支撐可傾瓦推力軸承在特定的設計參數(shù)下潤滑性能一致。 從理論的角度， 點支撐和線支撐推力軸承形成全膜潤滑所需流量隨著比壓的增加降低明顯， 這是因為膜厚隨著比壓增大減小。 固定瓦推力軸承流量功耗對坡高敏感。

3 不同支撐方式對推力軸承性能影響的工程分析

3.1 固定瓦推力軸承

結構一般為整塊平面上削出個瓦塊， 瓦塊之間有凹槽， 沿著液體流動方向形成收斂的間隙。瓦面加工平面度要求2 道， 但由于銅材料的加工難度大， 加之大型汽輪機組推力軸承直徑大， 瓦面加工平面度不易保證， 在場內總裝及現(xiàn)場總裝時通過接觸檢查修刮瓦面保證推力盤和瓦面的平面度， 由于大型汽輪機組的推力軸承尺寸大， 存在轉子軸承不對中造成的瓦塊不均勻承載現(xiàn)象。此外， 長期運行會導致平面部分磨損， 偏離最佳設計值。

潤滑方式一般為浸泡潤滑， 油從圓周方向某一角度的內緣進， 外緣出， 單推力盤油出口有時設置在推力盤和軸承構成的腔室上方， 有時為了及時排出一些熱油， 減小攪拌損失， 在腔室圓周方向其他角度也會設置排油孔， 這樣可能存在處在上方的瓦塊缺油的現(xiàn)象。 雙推力盤有時會在推力盤和軸承構成的腔室排油， 有時會沿著推力盤外緣整圈排油， 在工程上的應用效果即使同一種機組不同臺份同一個軸承都不一樣。

3.2 線支撐可傾瓦推力軸承

線支撐可傾瓦推力軸承瓦塊為單個瓦塊， 瓦背有一條支撐肋， 寬度一般小于20 mm,瓦塊支撐在墊環(huán)上， 瓦塊需要懸掛限位。 可能影響軸承性能的因素有以下幾個方面：

（1）瓦塊及墊環(huán)累計厚度不均， 墊環(huán)和瓦塊均有厚度及平面度要求， 裝配后會有累計誤差。

（2）擺動線是一條肋， 實際擺動時會沿著肋的棱邊擺動， 偏離理想的擺動節(jié)線位置， 由于肋的設置是比較窄的， 所以這一點對軸承性能的影響不大。

（3）限位不合理。 銷子限周向和徑向位， 環(huán)槽限軸向位， 設計間隙及加工誤差不匹配可能造成瓦塊擺動不良。

3.3 點支撐可傾瓦推力軸承

點支撐可傾瓦推力軸承有平衡式和非平衡式2種。 除了累計厚度偏差、 限位不當問題， Tieu[3]發(fā)現(xiàn)一種可逆的靜力失穩(wěn)現(xiàn)象， 目前還未發(fā)現(xiàn)文獻從理論上很好地揭示其機理。Tieu 在一推力盤直徑0.6 m， 最大推力負荷10 000 N， 最大轉速10 000 r/min 的試驗臺上， 對一點支撐可傾瓦推力軸承做了大量的載荷和轉速試驗， 得到了靜力穩(wěn)定性隨載荷、轉速變化的曲線，發(fā)現(xiàn)可逆的靜力失穩(wěn)現(xiàn)象。

4 總結

（1）在常規(guī)的設計比壓范圍（＜3.5 MPa）內， 2種軸承支撐方式不同是不會造成軸承性能不一致。

（2）工程經(jīng)驗表明， 瓦塊的不均載是造成瓦溫超過報警值的主要因素。 為了實現(xiàn)瓦塊均載， 軸承設計有自位球面推力軸承及帶均載塊的可傾瓦軸承， 但工程實踐表明這2 種結構都不是能實現(xiàn)絕對均載。 因此后續(xù)有必要分析影響瓦塊均載的因素， 指導產(chǎn)品的設計制造安裝。

（3）在比壓＞3.5 MPa 的情況下， 推力盤變形及瓦塊變形已成為不可忽略的因素。 推力盤相當于一個懸臂梁受力， 外圓變形最大， 點支撐的可傾瓦軸承允許繞支點做各個方向的擺動， 可以補償一部分變形， 因此當推力盤變形不可忽略時點支撐有一定的優(yōu)勢。 但因為瓦背支撐剛度低， 瓦塊變形因素也不可忽略， 因此可以考慮在軸承表面進行修型， 在冷態(tài)補償瓦塊變形。 雖然推力軸承設計目前技術成熟， 但極端工況下使用的高質量高性能軸承依然有待研究。

（4）軸承在工程上的應用屬于系統(tǒng)問題， 檢修安裝調整及機組運行控制等多方面因素均會影響軸承性能。