天然氣水合物試采井筒-土壤三維非線性耦合模型研究

暢元江，黃帥，王康，孫寶江，李昊，孫煥釗，陳國明

(1.中國石油大學(華東)海洋油氣裝備與安全技術研究中心，山東青島，266580；2.中國石油大學(華東)石油工程學院，山東青島，266580)

天然氣水合物井筒穩定性是井筒抵抗結構性破壞、維持井筒功能的重要屬性，是海洋水合物勘探開發過程中井下安全的保證。由于水合物具有埋藏淺、未成巖、強度低以及欠壓實等特點[1-2]，試采時，水合物分解的最直接效應是近井界面地層力學特性弱化，造成井筒失穩甚至套管損壞，因此，有必要考慮水合物分解引起的儲層物性參數在近井界面的時變特征，研究天然氣水合物三維井筒-土壤非線性耦合模型，并針對水合物儲層井筒的穩定性進行模擬分析。近年來，國內外學者對深水水合物開發過程中的井筒、井壁穩定性進行了大量研究。FREIJ-AYOUB等[3]根據摩爾-庫侖失效準則，利用單向達西流動模型分析水合物地層孔隙壓力變化，考慮孔隙壓力變化對應力場的影響，建立了水合物地層鉆井井壁穩定性模型；RUTQVIST 等[4-5]考慮天然氣水合物降壓開采過程中的滲流場、應力場和溫度場的耦合作用，對地層以及井筒的穩定性進行了分析，提出垂直井射孔段是最易出砂和應力集中的位置；KIM等[6]利用FLAC3D 軟件進行了油藏規模的熱-液-力耦合模擬，考慮井筒組件的尺寸和沉積物與井筒相互作用，分析了Ulleung 盆地天然氣水合物在降壓開采過程中高壓儲層的力學響應和井筒穩定性；NING等[7-9]研究了鉆井液侵入水合物地層條件下鉆井液參數(即溫度、密度、鹽度)和初始儲層條件(即滲透率和飽和度)對井筒穩定性的影響。程遠方等[10-11]將水合物分解效應融合到滲流場與巖土變形場的耦合作用中，建立了天然氣水合物藏氣、水兩相非等溫流固耦合數學模型，并開發了有限元程序；張若昕[12]從裸眼段井筒及套管段井筒2個方面對天然氣水合物開采過程中的井壁穩定性進行了研究；畢圓圓[13]建立了二維水合物地層-水泥環-套管力學模型，分析了孔隙壓力和溫度耦合作用對井筒應力的影響。上述研究為開展水合物試采井筒穩定性分析提供了理論依據，然而，這些研究多以二維為主平面模型為主，不能反映由于水合物分解導致的地層沉降對井筒的影響，且沒有考慮多場耦合下管土相互作用的時變特征。為此，本文作者基于海洋水合物井筒面臨的復雜環境載荷，考慮水合物分解效應，以井筒-儲層為研究對象建立水合物試采井的三維井筒-土壤非線性耦合模型，研究井筒-儲層之間隨時間變化的相互作用，揭示深海水合物儲層滲流場、應力場和井筒內外壓力場的耦合作用對井筒的力學響應規律，以便為我國海域天然氣水合物資源安全高效試采提供參考。

1 水合物分解多場耦合模型

1.1 Mohr-Coulomb 土壤本構模型

Mohr-Coulomb 模型可以較好地描述土體在彈性或塑性變形上的破壞機理[14]。土體在彈性階段的變形屈服方程如下：

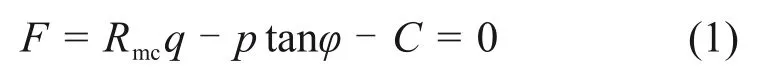
式中：F為土體剪切力，MPa；p為平均主應力；MPa；q為偏應力，MPa；Rmc為度量π 平面上屈服面形狀的參數；φ為土體摩擦角，即q-p面上Mohr-Coulomb屈服面的傾斜角；C為土體黏聚力，MPa。

當土體位于塑性變形階段時，在應力空間子午線上，流動勢G為雙曲線函數，可表示為

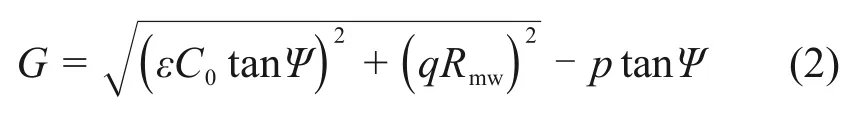
式中：Ψ為土體剪脹角；C0為土體塑性變形為0時的初始黏聚力，MPa；ε為子午線平面上的偏心率；Rmw為流動勢G在π平面上的形狀參數。

1.2 地層多孔介質滲流-變形模型

儲層巖石的受力主要為巖石骨架承受的有效應力和儲層孔隙流體的孔隙壓力。根據有效應力原理，土體內某一微元的靜力學平衡微分方程為

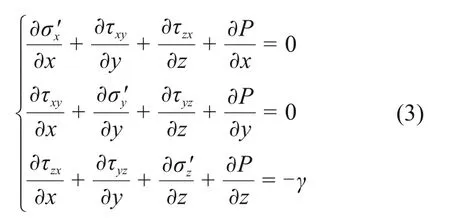
式中：τzx，τxy和τyz分別為xz，xy和yz平面的切應力；P為孔隙壓力；分別為x，y和z軸方向的單位孔隙壓力；σ′x，σ′y和σ′z分別為x，y和z軸方向的有效應力；γ為土的容重。

只考慮彈性變形情況時，土體形狀變化和有效應力改變需遵守胡克定律要求，其表達式如下：

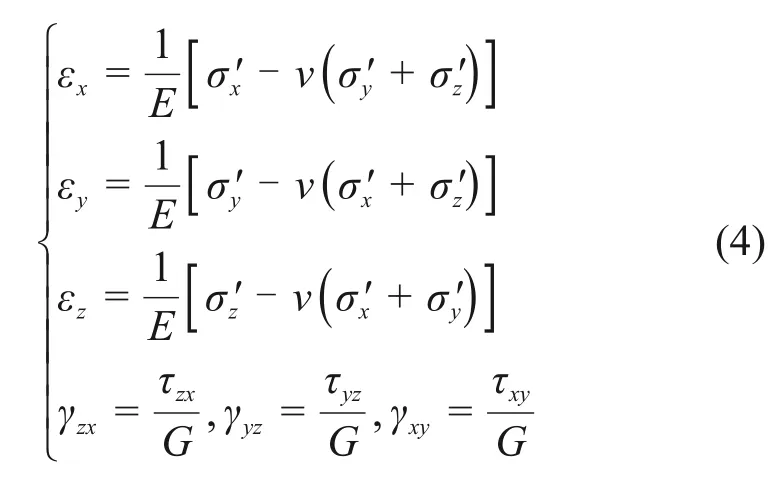
式中：E為土體骨架的彈性模量；v為泊松比；G為剪切模量，G=E/[2(1+v)]；εx，εy和εz分別為x，y和z方向的應變分量。

根據小變形理論，應變與位移的表達式為

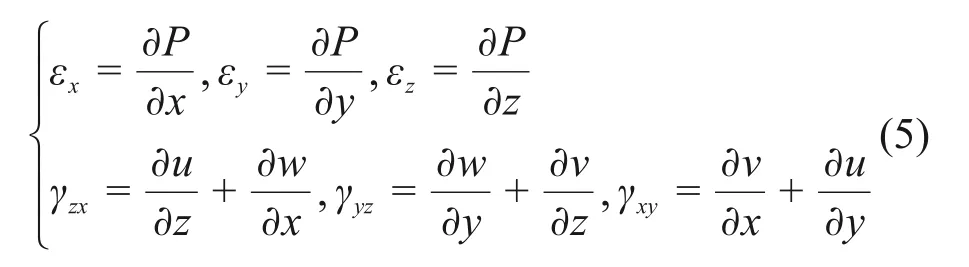
式中：u，v和w分別為x，y和z方向上的位移分量。

在水合物開采過程中，孔隙中水和氣體的壓力遠大于毛細管壓力，在此忽略毛細管作用，認為空隙中水和氣體壓力相等，考慮水合物分解對地層滲透系數的影響，采用比奧固結理論求解滲流-變形耦合模型：

單元體內水量的變化率等于土體積的變化率，由達西定律可得補充方程：

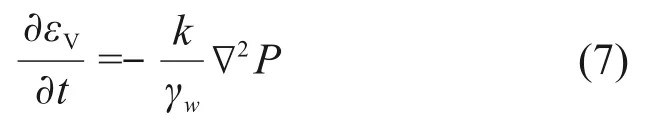
式中：γw為水的容重；k為滲透系數；εV=εx+εy+εz，為體積應變量。

1.3 水合物儲層物性參數動態變化模型

由于水合物分解效應，儲層物性參數將隨著水合物的開采發生變化，根據水合物儲層的滲透率、孔隙度與水合物的飽和度和土的體積應變建立函數關系[15-16]，得到滲透系數與孔隙度的動態計算模型：

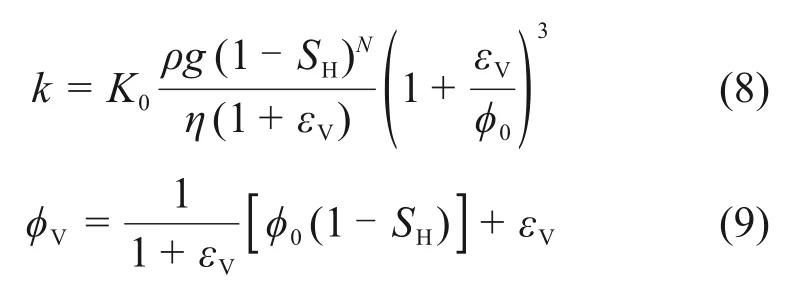
式中：SH為水合物儲層的飽和度；K0為絕對滲透率，即儲層SH=0 時的滲透率，10-3μm2；ρ為流體密度，kg/m3；g為重力加速度；η為動力黏滯性系數；φ0為初始孔隙度；N為地層滲透率遞減指數，由水合物賦存形式決定，通常取2～15。

在水合物開采過程中，水合物儲層的強度和膠結特性等會伴隨水合物的分解逐步降低和減弱，表現為水合物儲層彈性模量減小以及黏聚力呈線性軟化[17]，在鉆采過程中，水合物儲層彈性模量、黏聚力與水合物飽和度相關的計算模型可以表示為

式中：E0為水合物未分解時的彈性模量，GPa；SH0為水合物儲層的初始飽和度；Δφ=φ0(SH0-SH)，為水合物分解引起的地層孔隙度變化量；ξ為實驗擬合參數，通常取9.5；ψ取為1.2。

對于我國南海海域廣泛存在的膠結或骨架支撐型水合物，在實際模擬過程中需要不斷地更新調整相應的力學參數和滲流參數。式(1)和式(2)描述的Mohr-Coulomb 本構模型可作為水合物地層的土壤模型；式(7)可為Mohr-Coulomb土壤模型計算提供勁度矩陣，用來控制三維滲流過程中地層的變形；式(8)～(11)可為水合物開采模擬中儲層物性參數的變化提供計算依據。

2 三維井筒-土壤非線性耦合模型建模方法

2.1 水合物試采井井身結構

由于海洋水合物儲層埋藏淺、未固結，井身結構采用如圖1所示的三開方式，儲層段采用套管不固井完井[18-19]，通過降低儲層壓力，進行水合物降壓開采。

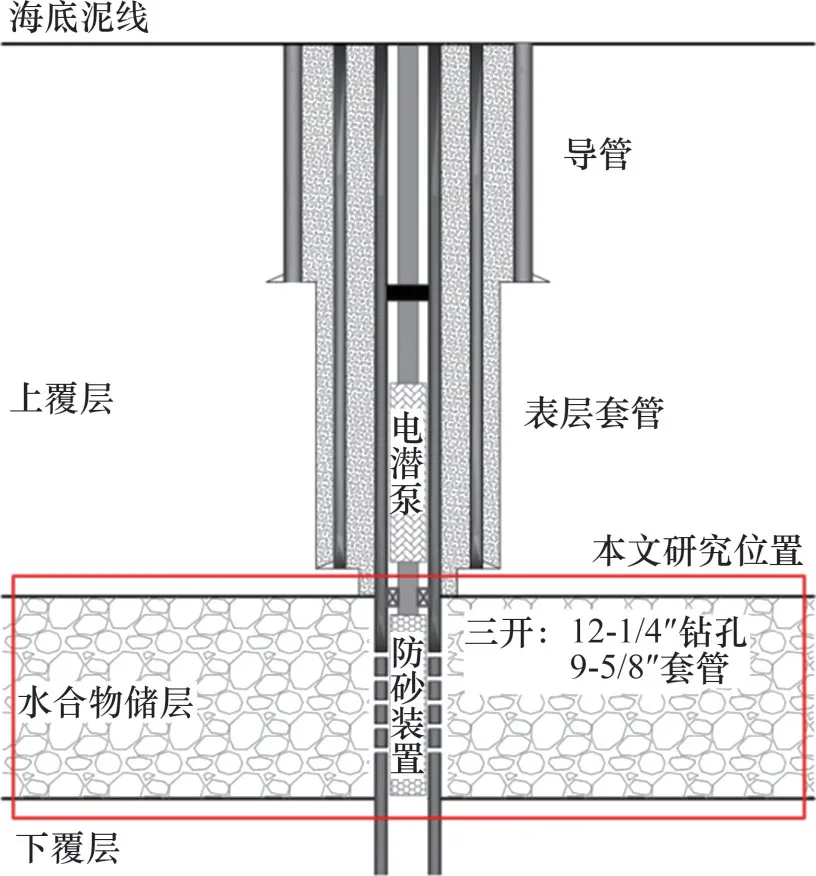
圖1 天然氣水合物試采井井身結構Fig.1 Well structure of gas hydrate production test well

本文選取受水合物分解影響最顯著的儲層段井筒作為研究對象，其力學模型如圖2所示。通過有限元軟件建立三維實體模型，研究水合物在試采過程中井筒與地層隨時間的變化。為此，編寫了水合物分解多場耦合模擬程序，進而對試采過程中水合物分解進行模擬。

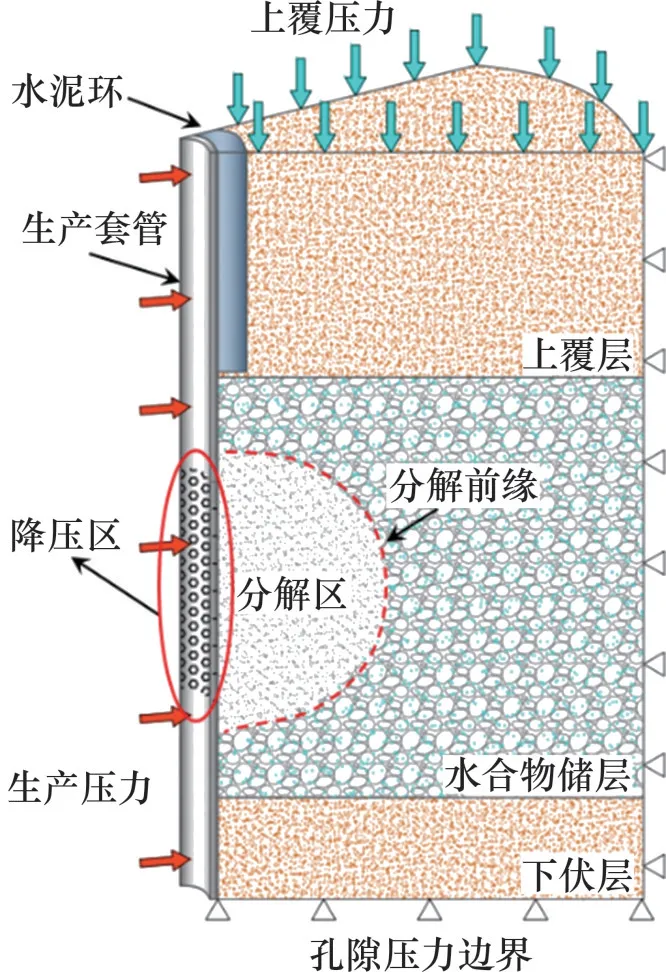
圖2 儲層段井筒力學模型Fig.2 Wellbore mechanics model of reservoir section

2.2 水合物分解多場耦合模型的建立

在水合物試采時，儲層孔隙流體流失，孔隙壓力水平降低，使水合物相變分解，導致巖石骨架的應力狀態發生變化，相應的儲層滲透率、孔隙度等物性參數隨之改變，這些由孔隙流體流失造成的儲層變化又會對孔隙流體的滲流過程產生影響，這是一個復雜的非線性耦合過程。本文利用建立的滲流-變形耦合模型與水合物儲層物性參數動態變化模型，對ABAQUS 進行二次開發，基于Fortran 語言對模型積分點的場變量進行重新定義，開發編寫了水合物模擬求解器。考慮水合物分解引起的儲層應力場、滲流場和井筒內外壓力場的特征參數在近井界面區域的時變特征，對水合物開采過程中多場耦合作用下的井筒受力進行模擬，計算流程如圖3所示。

圖3 多場耦合分析計算流程Fig.3 Flow chart of multi-field coupling analysis

進行多場耦合分析時，首先定義儲層物性參數隨場變量的變化；然后，對壓力場與滲流場進行計算，通過調用場變量子程序USDFLD 對水合物分解區域的儲層物性參數進行實時更新，以此實現管土相互作用邊界的動態變化；根據更新的邊界對下一個增量步進行求解，直至達到設定的模擬分析時長為止。

2.3 三維井筒-土壤非線性耦合模型實現

按以下步驟建立三維井筒-土壤非線性耦合模型(見圖4)：

圖4 三維井筒-土壤非線性耦合模型建模流程Fig.4 Modeling flow chart of 3D nonlinear coupling wellbore-soil model

1)確定研究位置的水合物地層物性參數和井筒結構參數，建立有限元幾何模型。

2)建立滲流-變形耦合模型和水合物儲層物性參數動態變化模型。

3)根據建立的水合物分解多場耦合數學模型編寫場變量子程序，模擬水合物的分解。

4)對模型賦予初始預定義場(地應力場和孔隙壓力場)以及管土相互作用邊界。

由于材料剛度存在差異，井筒與水合物地層之間的界面處產生摩擦力，這些摩擦力導致井筒產生軸向應力。在定義管土相互作用時，采用接觸面法，套管表面為主控表面，土體表面為從屬表面；考慮管土接觸界面之間存在黏聚力，管土間法向接觸定義為修正的硬接觸，切向接觸定義為具有各向同性的庫侖摩擦，采用罰函數法求解。

3 算例分析

3.1 三維非線性耦合模型基本參數

本研究采用的數值模擬參數來源于我國神狐海域某水合物試采井，水深為1 230 m，上覆土層厚度為200 m，基本參數如表1所示[20-21]。

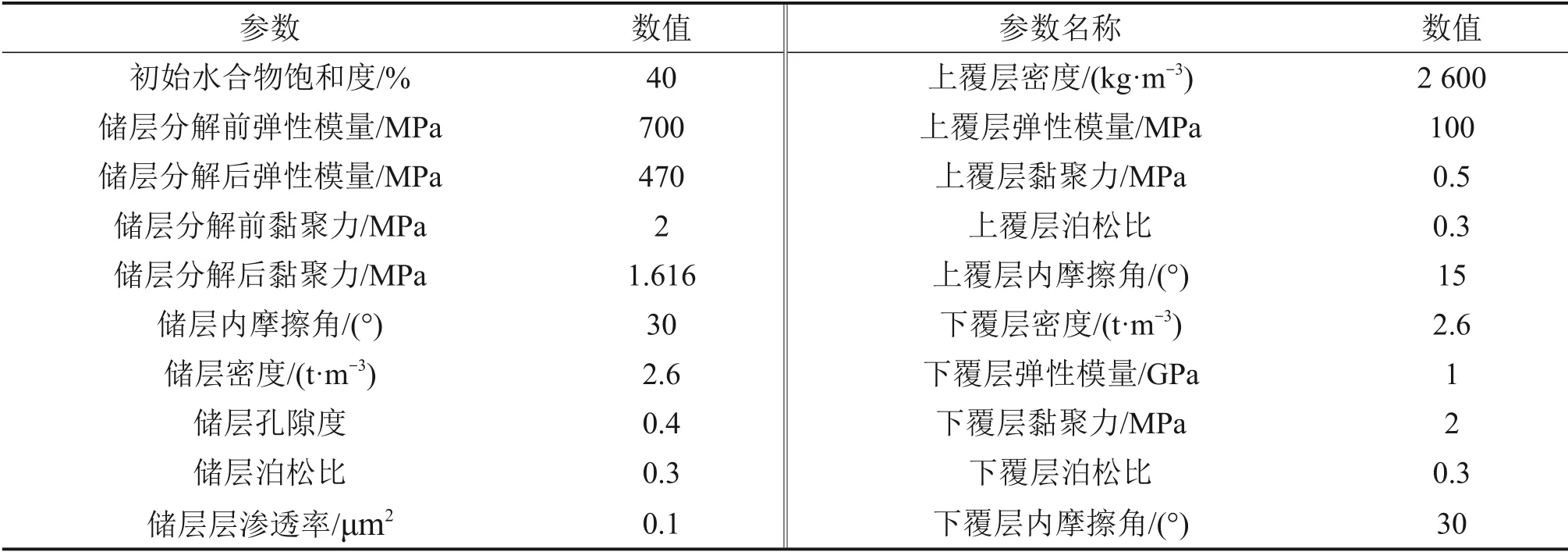
表1 天然氣水合物藏地層物性參數Table 1 Formation physical parameters of gas hydrate reservoir

在建立管土耦合模型時，為了避免模型端部邊界效應的影響，模型參數選取如下[22]：地層設置為長×寬×高為5 m×10 m×17 m 的長方體，其中上覆層厚度為5 m，水合物儲層厚度為10 m，下伏層厚度為2 m，水泥環的長度為5 m，套管貫穿整個地層的長度取17 m。井筒基本參數如表2所示。

表2 井筒基本參數Table 2 Basic parameters of wellbore

3.2 基于三維非線性耦合模型的井筒穩定性分析

利用圖4所示流程圖進行建模分析。由于套管和水合物地層的結構及載荷呈對稱性，且在井筒與地層膠結良好的情況下，建模型時可沿加載方向取模型的1/2 進行分析，如圖5所示。在模型的上表面施加海水及上覆巖層等效壓力15 MPa，儲層土體受重力的作用，對土體上、下以及四周表面賦予初始滲透壓力，在套管內壁施加生產壓力；在模型底部對土體和套管施加U3方向的位移約束，在土體外表面施加U1和U2方向的位移約束，以模擬周圍地層對模型的約束作用。給模型對稱面施加對稱約束。對土體賦予地應力、初始孔隙壓力、孔隙比等預定義場后，進行地應力平衡計算，結果見圖6。由圖6可知儲層的位移數量級為10-7m，遠小于地應力平衡要求的位移數量級10-5m，表明符合地應力平衡條件，可以進行下一步計算。

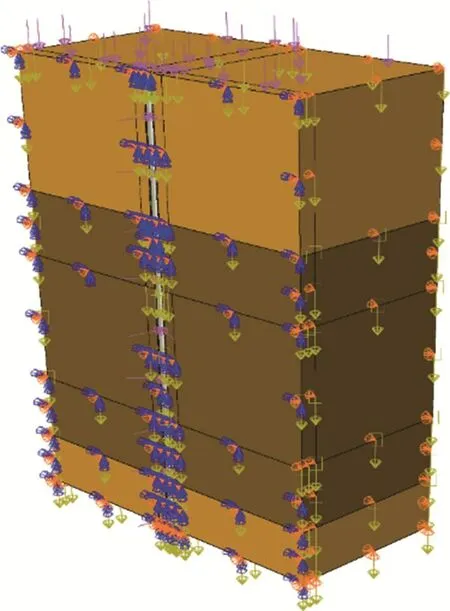
圖5 載荷和邊界條件Fig.5 Loading and boundary conditions

圖6 地應力平衡結果Fig.6 Result of geo stress balance

天然氣水合物的開采與常規油氣的最主要區別在于開采過程存在水合物的分解效應。圖7和圖8所示分別為以10 MPa 的生產壓差試采60 d 后孔隙壓力和水合物飽和度分布情況。從圖7和圖8可以看出：隨著開采生產過程進行，儲層中的孔隙壓力從生產區域向周圍地層逐漸增加，越靠近井眼位置，孔隙壓力越小，孔隙壓力變化梯度越大；井筒周圍儲層的水合物飽和度隨著開采逐漸降低，且水合物完全分解區域與未分解區域的過度區域較窄。

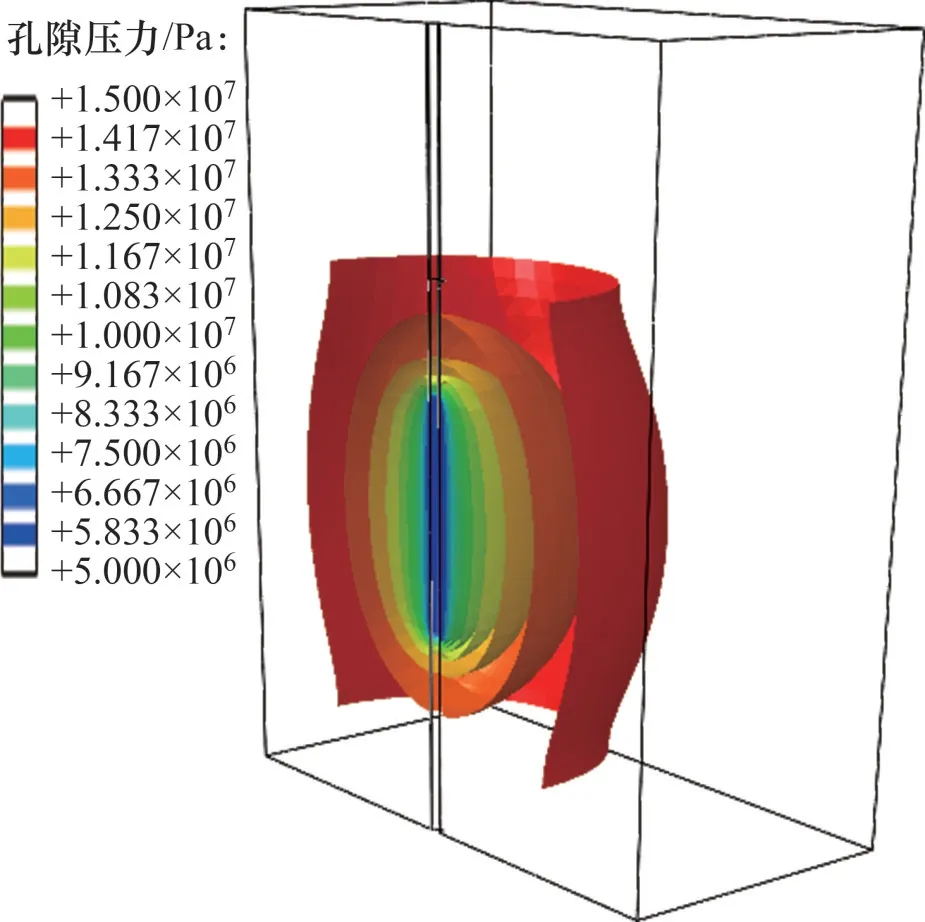
圖7 孔隙壓力分布云圖Fig.7 Nephogram of pore pressure distribution

圖8 水合物飽和度分布云圖Fig.8 Nephogram of hydrate saturation distribution

在試采井系統中，井筒是否穩定關系到試采作業能否安全、順利進行，影響井筒穩定性的關鍵因素為試采井井筒中套管的受力。儲層段井筒應力情況如圖9所示，圖中正值表示套管受到的是拉應力，負值表示套管受到的是壓應力。從圖9可以看出：由于水合物的分解，水合物儲層下沉和下伏地層向上隆起，使得儲層段井筒產生較大的軸向壓應力，且套管的最大軸向壓應力位于儲層段套管中部即降壓開采的位置；套管最大環向應力同樣位于儲層段套管中部降壓開采位置，套管受到的徑向應力可忽略不計。套管Mises應力的變化主要受軸向應力影響，其變化趨勢與軸向應力變化趨勢基本一致，表明軸向應力可以作為井筒穩定性的判據。

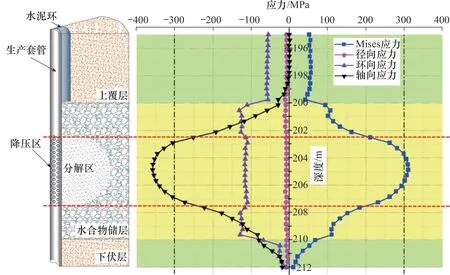
圖9 儲層段井筒套管應力分布Fig.9 Stress distribution of wellbore casing in reservoir section

3.3 井筒穩定性影響因素分析

3.3.1 初始水合物飽和度對井筒穩定性的影響

以生產壓差為13 MPa，試采時間為30 d為例，分別模擬水合物初始飽和度為20%，40%和60%時井筒的穩定性，套管軸向應力情況如圖10所示。

由圖10可知：在水合物初始飽和度為20%，40% 和60% 時，套管的最大軸向應力分別為-472.76，-417.00 和-381.10 MPa(負號表示軸向應力方向向下)，表明在相同的試采時間和溫壓條件下，儲層初始水合物飽和度越小，儲層段套管受到的軸向應力就越大，井筒的穩定性越差。這主要是因為水合物初始飽和度越高，儲層滲透率相對越低，從而降低了孔隙壓力的降壓速率，減慢了水合物分解的進程。

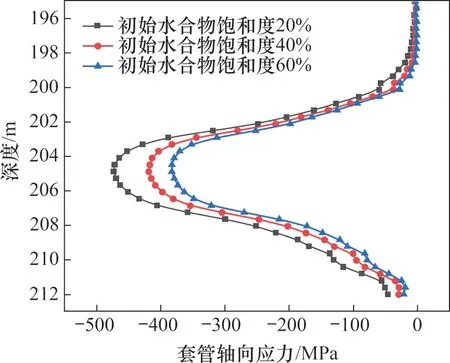
圖10 不同初始水合物飽和度對套管軸向應力分布的影響Fig.10 Influence of different initial hydrate saturations on the axial stress distribution of casing

3.3.2 生產壓差對井筒穩定性的影響

設定儲層初始水合物飽和度為40%，試采生產時間為10 d，分析生產壓差為5，8，10，12 和和13 MPa 共5 種試采條件下井筒的穩定性，套管軸向應力如圖11所示。

由圖11可知：套管的軸向應力隨著生產壓差的增加而增加，其中，當生產壓差由5 MPa增加到8 MPa 時，套管的最大軸向應力由154.1 MPa 增加到246.9 MPa，增大了60.22%，可見生產壓差越大，儲層水合物的分解速率越快，范圍越廣，相應的儲層段套管因地層有效應力變化受到的壓力也更加大。這與常規疏松砂巖油氣藏開采所得到的結果類似。

圖11 不同生產壓差對套管軸向應力分布的影響Fig.11 Influence of different production pressures on axial stress distribution of casing

3.3.3 試采時間對井筒穩定性的影響

設定儲層初始水合物飽和度為40%，生產壓差壓為10 MPa，在試采時間分別為1，5，10，30和60 d 時，套管軸向應力如圖12所示。參照API標準，考慮到水合物儲層生產段套管存在射孔情況，選取N-80 套管屈服強度552 MPa 的60%即331.2 MPa 作為參照[23]，分析不同生產壓差下套管軸向應力與生產時間的關系，如圖13所示。

由圖12和圖13可知：隨著生產壓差提高和試采時間延長，井筒的軸向應力逐漸增加，且軸向應力在試采初期增加較明顯，隨著試采進行逐漸趨于平穩；當生產壓差為13 MPa與12 MPa時，最大軸向應力在試采初期就超過了套管的屈服強度(331.2 MPa)，若生產壓差為10 MPa，則安全試采僅能維持15 d；若生產壓差不超過8 MPa，則安全試采可達60 d以上。

圖12 不同試采時間對套管軸向應力分布的影響Fig.12 Influence of different production time on axial stress distribution of casing

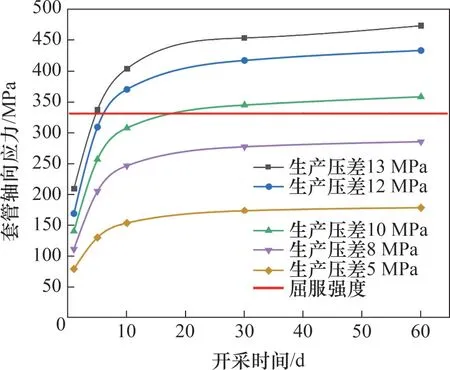
圖13 不同生產壓差下套管軸向應力與生產時間的關系Fig.13 Relationship between casing axial stress and production time in different production pressures

4 結論

1)基于海洋水合物井筒面臨的復雜環境載荷，考慮滲流場、應力場和井筒內外壓力場的多場耦合作用，研究了水合物分解引起的儲層特征參數在近井界面區域的時變特征，開發編寫了水合物場變量子程序，提出了天然氣水合物井筒-土壤三維非線性耦合模型建模方法。

2)在水合物試采過程中，由于水合物的分解，水合物儲層下沉和下伏地層向上隆起，使得儲層段井筒產生較大的軸向壓應力，井筒穩定性受井筒軸向應力所控制，套管的最大軸向應力位于儲層段套管中部即降壓開采的位置。

3)隨著生產壓差提高和試采時間延長，井筒的軸向應力逐漸增加，且軸向應力在試采初期增加較明顯，隨著試采進行逐漸趨于平穩；若生產壓差超過10 MPa，則安全試采僅能維持15 d；若生產壓差不超過8 MPa，則安全試采可達60 d以上。