基于2CRU/2PRRR并聯式灌裝機構的設計與工作空間分析

劉建國，馬春生，文杰，李瑞琴，屈淑維

基于2CRU/2PRRR并聯式灌裝機構的設計與工作空間分析

劉建國，馬春生，文杰，李瑞琴，屈淑維

（中北大學 機械工程學院，太原 030051）

針對目前流水線上的灌裝機構，對含有不同傾角瓶子的通用性不強等問題，提出一種新型2CRU/2PRRR并聯機構來解決這一問題。首先用SolidWorks軟件創建2CRU/2PRRR并聯機構的立體模型。利用螺旋理論分析得出該機構的自由度，并用修正的Kutzbach-Grübler公式對分析得出的自由度進行驗證。然后利用運動學模型和D-H法分析求解機構動平臺的位置反解。最后應用Matlab軟件編寫相應的極限邊界搜索程序，運算求解出工作空間，并給出該灌裝機構在流水線的應用實例。2CRU/2PRRR并聯機構擁有1個轉動自由度，3個方向的移動自由度。工作空間為規則立方體，內部連續無空洞且無奇異位型。2CRU/2PRRR并聯式灌裝機構結構簡單、運行穩定、性能良好，完全可以滿足流水線上對含有傾角的瓶子進行灌裝時的運動和工作范圍需求，提高了灌裝機構的通用性。

2CRU/2PRRR；并聯機構；螺旋理論；位置反解；工作空間

并聯機構相較于串聯機構而言，通常具有一些獨特的性能，例如剛度大、精度高、速度高、誤差小、對稱結構具有良好的各向同性等優點。并聯機構在包裝機械行業中應用十分廣泛，如灌裝機械、封袋機械、噴碼機、分揀機械、碼垛機械等。并聯機器人的應用有利于提高生產效率，降低工人的勞動強度。目前，在包裝機械行業中一般3～4個自由度就能夠完成工作要求，而大部分少由度的并聯機構擁有結構簡單，價格低廉，容易控制，便于大規模應用等優點，因而成為了包裝機械行業應用研究的新熱點。

在現代先進制造的大背景下，在包裝機械行業中對于并聯機器人的研究成果有很多，如尹曉秦等[1]提出了一種用于解決流水線上不同斜面貼標問題的含有閉環的并聯機構。崔馬茹等[2]提出了一種用于對灌裝瓶子進行壓蓋工序的3-URPR并聯機構。王新宇等[3]提出了一種用于解決不同斜面上旋蓋問題的2-PSR/UPU并聯機構。米文博等[4]提出了一種用于藥品的裝箱和碼垛環節的2-UPR/RSPR并聯機構。馬振東等[5]提出了一種用于代替人進行分揀作業的新型2-RPS/UPRS并聯機構。近些年來在學術界中對于少自由度的并聯機構也進行了大量研究，提出許多新構型，為工程應用奠定良好基礎。如郭東杰等[6]對3-CRU并聯機構，進行了動力學建模和分析。寇月陽等[7]對3PRRR并聯機構進行了設計與優化；尹小琴等[8]對三平移并聯機構3-RRC的工作空間進行了分析。李秦川等[9]重點對并聯機構的構型綜合、運動性能分析和尺度綜合三方面的研究進行了總結分析。付萌[10]對少自由度并聯機構尺度參數的多目標優化進行了研究。

當前，在液體物料生產中，有許多物料如飲料方面的汽水、果汁、牛奶、啤酒等，調味品方面的醬油、醋、果醬等，生活用品方面的洗潔精、洗面奶等都需要進行灌裝工序。目前流水線上所用的灌裝機構種類繁多，例如：旋轉型灌裝機、直線型灌裝機等，但大多數灌裝機只能對直口瓶子進行灌裝，而對含有傾角瓶子就不適用了，因此文中擬提出一種2CRU/2PRRR四自由度并聯機構用于灌裝行業，以提高灌裝機構的通用性。

1 2CRU/2PRRR并聯機構的自由度分析

1.1 機構設計與建立坐標系

2CRU/2PRRR并聯機構見圖1，該機構由1個定平臺、1個動平臺、2條CRU支鏈和2條PRRR支鏈組成。其中，CRU支鏈由1個C副（圓柱副）、1個R副（轉動副）和1個U副（虎克鉸）組成，PRRR支鏈包由1個P副（移動副）和3個R副（轉動副）組成。

圖1 2CRU/2PRRR并聯機構

在2CRU/2PRRR并聯機構上建立坐標系，見圖2。定平臺是邊長為的正方形，1、2、3、4分別為4個頂點；動平臺是邊長為的正方形，1、2、3、44點分別為動平臺各個邊長的中點。以定平臺的幾何中心0為定坐標系原點，0軸平行于12，0軸平行于23，0軸垂直于平面1234向上，建立坐標系0-000；以動平臺的幾何中心1為動坐標系原點，1軸與42平行，1軸與13平行，1軸與面1234垂直向上，建立坐標系1-111。

圖2 2CRU/2PRRR并聯機構坐標系

基于節能環保的理念，為降低成本、降低環境污染以及能源消耗、提高機構的操作性能，在保證機構的運行性能完全能夠滿足工作要求的情況下，盡可能地減輕機構重量，降低運行時的功耗。該機構采用輕型材料來替代金屬材料以降低桿件的重量，實現減輕機構重量和提升運行性能的目的；同時滿足工作時所需的強度和剛度要求下，應用形狀優化的方法，對該機構進行輕量化設計。通過輕量化設計后，該機構因為整體重量降低了，運行起來更加靈活穩定，同時也實現了工作效率的提高以及資源的最優化配置，這對推動建設環保低碳經濟型社會的發展具有重要意義。

1.2 自由度分析

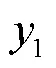
CRU支鏈的運動螺旋系為：

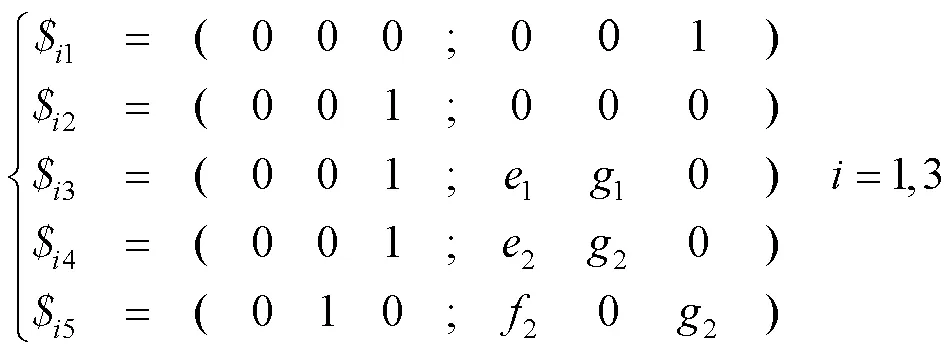
對式（1）求反螺旋系，可得：

其次，對PRRR支鏈進行自由度分析，設PRRR支鏈的動坐標系為2-222，2軸垂直于23水平向右，2軸平行于23，2軸由右手螺旋定則可得，見圖2。

PRRR支鏈的運動螺旋系為：

對式（3）求反螺旋系，可得：

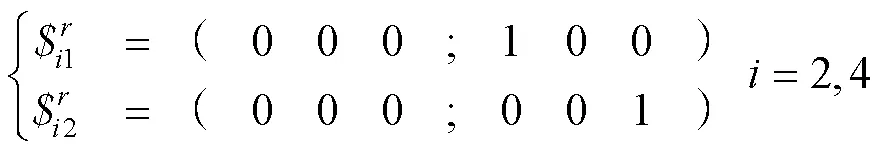
整合式（2）和式（4），再次求其反螺旋，則得到2CRU/2PRRR并聯機構的運動螺旋系為：

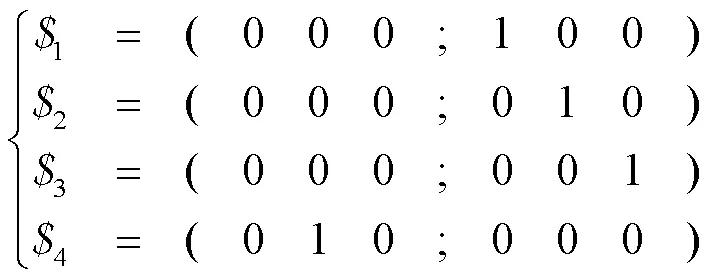
經過對式（5）進行分析得知，2CRU/2PRRR并聯機構的動平臺含有4個自由度，分別是沿0軸、0軸、0軸方向的3個移動自由度，以及1個繞0軸方向的轉動自由度。

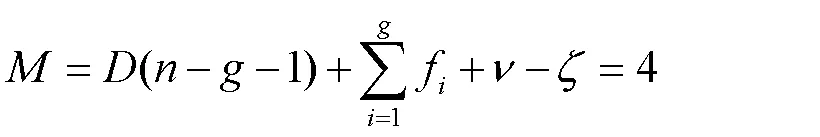
經過K-G公式的計算，可證實該機構具有4個自由度。沿0軸、0軸的2個移動自由度的目的是為了調整下料口與瓶口的水平距離，沿0軸的移動自由度是為了調整下料口與瓶口的垂直距離，繞0軸的轉動自由度是為了調整下料口的傾斜角度，更好地適應斜口瓶的灌裝。

2 2CRU/2PRRR并聯機構的位置反解

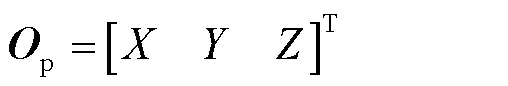
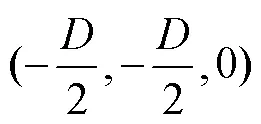
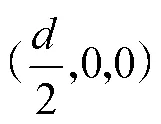
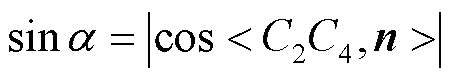
通過式（7）—（9）可知，CUR支鏈的位置反解為：

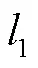
圖3 PRRR支鏈的D-H變換坐標系

然后建立D-H參數，見表1。表1中，參數、、1、2為已知量，參數2、3、4、2為未知量。

表1 PRRR支鏈的D-H參數

Tab.1 D-H parameters of PRRR branch chain

利用參數表中的數據，將歐拉角位姿矩陣與D-H坐標變換矩陣進行分析，由此可以反解出2、3、4、2，計算過程見式（11）—（14）。

D-H坐標變換矩陣：

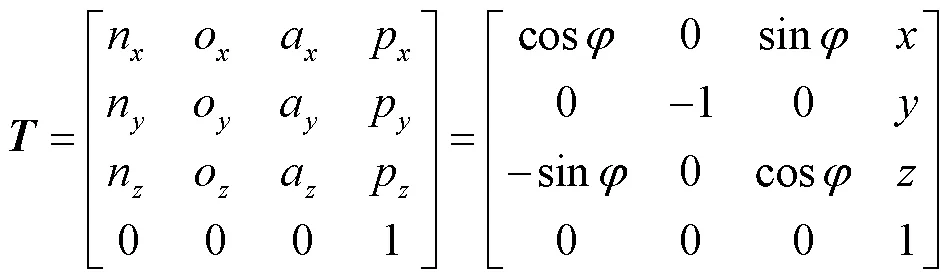
經過化簡計算，可得到PRRR支鏈的位置反解2、2：

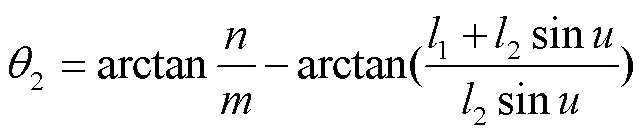
式中：

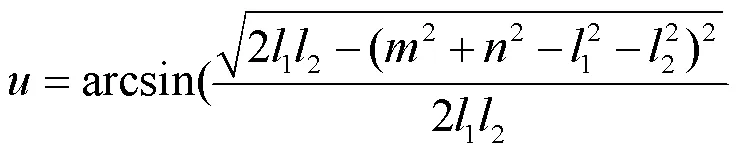
3 2CRU/2PRRR并聯機構的工作空間分析

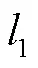
通過觀察圖4可知，2CRU/2PRRR并聯機構在空間中有較大的工作范圍，工作空間形狀為立方體，能夠更好地適應流水線工作，且在整個工作空間內部連續、緊湊、無空洞，表明該并聯機構運行連續、平穩，具有良好的運行性能[17-18]。

4 2CRU/2PRRR并聯機構的應用

2CRU/2PRRR并聯機構可用于流水線上的灌裝工作，應用示意圖見圖5。其中，圖5a為該機構在對直口瓶子進行灌裝的過程，圖5b為該機構對含有傾角的瓶子進行灌裝的過程。首先，將位于該機構4條支鏈底部的支撐點分別與預設在傳輸帶兩邊的安裝孔一一對應，并使之固定連接。然后當傳輸帶將待裝瓶傳送至灌裝機構的工作范圍內時，根據瓶口的位置調整下料口的姿態，使下料口對準瓶口。當下料口對準瓶口后，置于下料口末端的灌裝閥將自動打開，位于動平臺上的儲液箱里的待裝液料就會通過下料管流入瓶子內，從而實現灌裝工序。當灌裝工序完成后，灌裝閥將自動關閉，下料口升起離開瓶口，開始下一個瓶子的灌裝工序。其中，下料口位于動平臺中心處下端，下料口呈“錐形”口，目的是方便使其對準瓶口。最后，利用SolidWorks創建2CRU/2PRRR并聯式灌裝機構的虛擬樣機，根據灌裝時對于工作路徑的需求，對樣機加以相應的程序控制進行運動仿真，在仿真過程中，該機構在流水線上不僅能夠對直口瓶子進行灌裝工序，也可以對含有不同傾角的瓶子進行灌裝工序。由此結果可以顯示該機構運行平穩、精確、迅速，能夠精準地完成灌裝任務。不但提高了灌裝機械的通用性，而且也大大提高了工作效率。

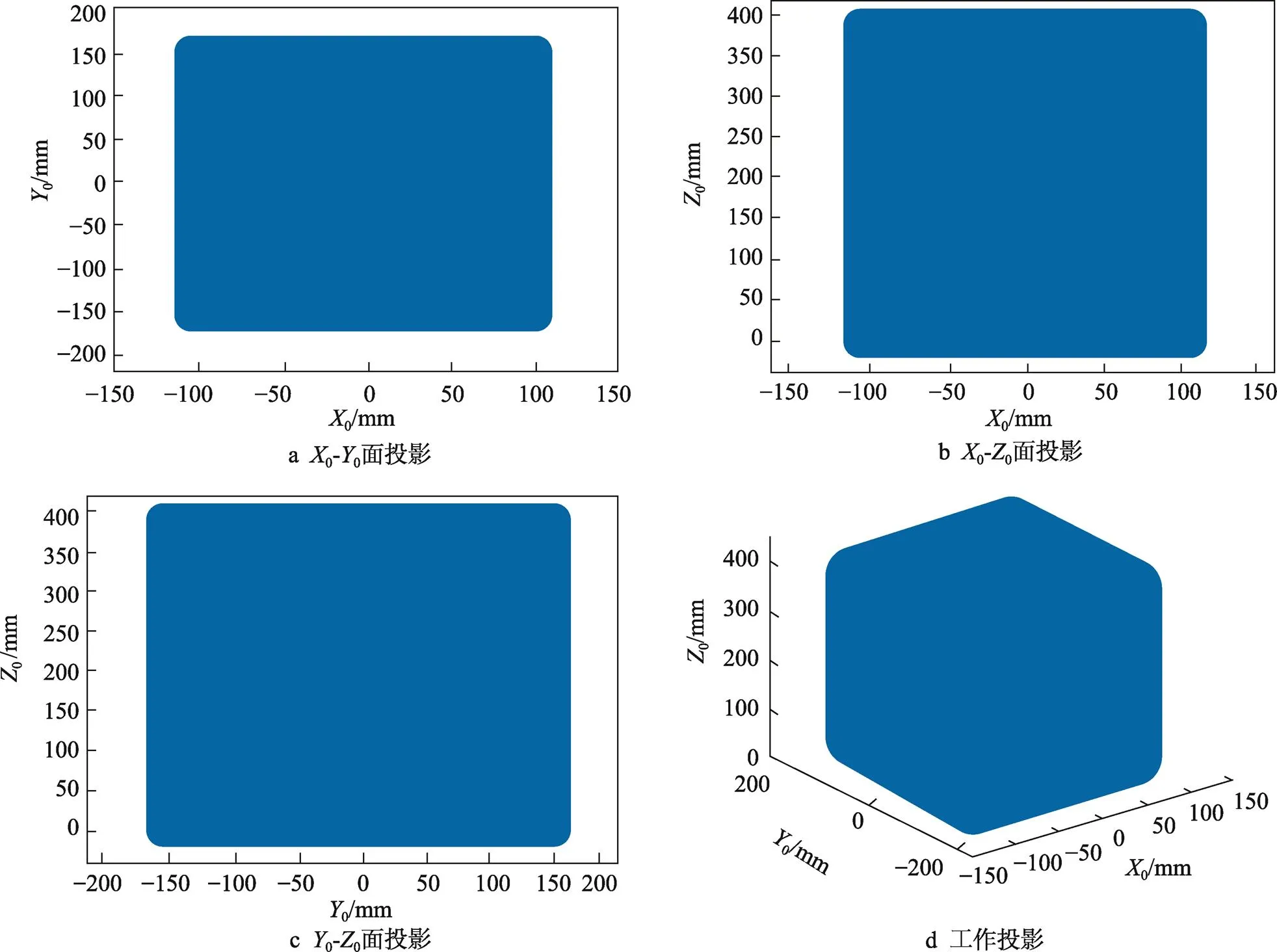
圖4 2CRU/2PRRR并聯機構的可達工作空間

圖5 2CRU/2PRRR并聯機構應用實例

5 結語

文中提出用于流水線上的2CRU/2PRRR并聯式灌裝機構，首先基于螺旋理論對其自由度進行分析，得出該并聯機構擁有4個自由度，即沿0、0、0軸方向的移動自由度和繞0軸的轉動自由度，完全可以滿足流水線上對含有傾角的瓶子進行灌裝時的運動需求，并利用修正Kutzbach -Grübler公式對得到的自由度加以驗證，結論無誤；然后利用動力學模型分析法和D-H法，聯合兩者對2CRU/2PRRR并聯機構進行了位置反解，通過Matlab求解并繪制出了該并聯機構的工作空間，工作空間的形狀為立方體，連續、無空洞，表明該機構運行連續且靈巧，工作性能良好，完全能夠滿足運行時的工作范圍要求。最后給出了該并聯機構的工程應用實例。2CRU/2PRRR并聯式灌裝機構大大提高了灌裝機構的通用性，同時也提升了灌裝工作效率，該并聯機構可以有效地應用在實際生產過程中。

[1] 尹曉秦, 馬春生, 米文博, 等. 含有閉環的并聯貼標機構運動學分析[J]. 包裝工程, 2021, 42(3): 185-189.

YIN Xiao-qin, MA Chun-sheng, MI Wen-bo, et al. Kinematic Analysis of Labeling Mechanism Based on Closed-Loop Parallel Mechanism[J]. Packaging Engineering, 2021, 42(3): 185-189.

[2] 崔馬茹, 武建德, 李瑞琴, 等. 3-URPR并聯機構的逆運動學與可達工作空間分析[J]. 包裝工程, 2020, 41(21): 196-201.

CUI Ma-ru, WU Jian-de, LI Rui-qin, et al. Inverse Kinematics and Reachable Workspace of 3-URPR Parallel Mechanism[J]. Packaging Engineering, 2020, 41(21): 196-201.

[3] 王新宇, 李虹, 李亞麗, 等. 基于2-PSR/UPU并聯機構的旋蓋裝置設計及性能分析[J]. 包裝工程, 2020, 41(3): 188-193.

WANG Xin-yu, LI Hong, LI Ya-li, et al. Design and Performance Analysis of a Novel Capping Device Based on 2-PSR/UPU Parallel Mechanism[J]. Packaging Engineering, 2020, 41(3): 188-193.

[4] 米文博, 馬春生, 李瑞琴, 等. 應用于藥品包裝生產線的2-UPR/RSPR并聯機構的工作空間分析[J]. 包裝工程, 2021, 42(3): 171-176.

MI Wen-bo, MA Chun-sheng, LI Rui-qin, et al. Workspace of 2-UPR/RSPR Parallel Mechanism Applied to Medicine Packaging Production Line[J]. Packaging Engineering, 2021, 42(3): 171-176.

[5] 馬振東, 馬春生, 米文博, 等. 基于2-RPS/UPRS并聯機構的自動分揀機運動分析[J]. 包裝工程, 2021, 42(1): 157-162.

MA Zhen-dong, MA Chun-sheng, MI Wen-bo, et al. Kinematics Analysis of Automatic Sorter Based on 2-RPS/UPRS Parallel Mechanism[J]. Packaging Engineering, 2021, 42(1): 157-162.

[6] 郭東杰, 李楊民, 李彬. 一種新型3-CRU并聯機構的動力學建模[J]. 機械工程與技術, 2016, 5(4): 344-351.

GUO Dong-jie, LI Yang-min, LI Bin, et al. Kinetic Modeling of a Novel 3-CRU Translational Parallel Mechanism[J]. Mechanical Engineering and Technology, 2016, 5(4): 344-351.

[7] 寇月陽, 陳柏, 吳洪濤, 等. 3PRRR并聯機構的設計與優化[J]. 機械設計與制造, 2015(3): 152-154.

KOU Yue-yang, CHEN Bai, WU Hong-tao, et al. The Design and Optimization of 3PRRR[J]. Machinery Design & Manufacture, 2015(3): 152-154.

[8] 尹小琴, 馬履中. 三平移并聯機構3-RRC的工作空間分析[J]. 中國機械工程, 2003, 14(18): 1531-1533.

YIN Xiao-qin, MA Lv-zhong. Workspace Analysis of a 3-DOF Translational Parallel Mechanism 3-RRC[J]. China Mechanical Engineering, 2003, 14(18): 1531-1533.

[9] 李秦川, 柴馨雪, 陳巧紅. 兩轉一移三自由度并聯機構研究進展[J]. 科學通報, 2017, 62(14): 1507-1519.

LI Qin-chuan, CHAI Xin-xue, CHEN Qiao-hong. Review on 2R1T 3-DOF Parallel Mechanisms[J]. Chinese Science Bulletin, 2017, 62(14): 1507-1519.

[10] 付萌. 少自由度并聯機構尺度參數的多目標優化研究[D]. 成都: 電子科技大學, 2013: 59-69.

FU Meng. Multi-Objective Optimization Dimensional Design of Lower-Mobility Parallel Manipulators[D]. Chengdu: University of Electronic Science and Technology of China, 2013: 59-69.

[11] 張國慶, 杜建軍. 基于螺旋理論的空間機構自由度分析方法[J]. 機械設計與制造, 2009(1): 10-12.

ZHANG Guo-qing, DU Jian-jun. Analysis of Spatial Mechanisms Based on the Screw Theory[J]. Machinery Design & Manufacture, 2009(1): 10-12.

[12] 黃真, 趙永生, 趙鐵石. 高等空間機構學[M]. 2版. 北京: 高等教育出版社, 2014: 111-152.

HUANG Zhen, ZHAO Yong-sheng, ZHAO Tie-shi. Advanced Spatial Mechanism[M]. Beijing: Higher Education Press, 2014: 111-152.

[13] 于靖軍, 劉辛軍, 丁希侖, 等. 機器人機構學的數學基礎[M]. 北京: 機械工業出版社, 2008: 101-188.

YU Jing-jun, LIU Xin-jun, DING Xi-lun, et al. Mathematical Foundations of Mechanism Robotics[M]. Beijing: China Machine Press, 2008: 101-188.

[14] 石志新, 葉梅燕, 羅玉峰, 等. 3T1R并聯機構結構設計與位置分析[J]. 農業機械學報, 2016, 47(8): 364-369.

SHI Zhi-xin, YE Mei-yan, LUO Yu-feng, et al. Structure Design and Displacement Analysis of 3T1R Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8): 364-369.

[15] 范建會, 趙新華, 李彬. 一種新型三自由度并聯機構逆運動學及其工作空間分析[J]. 天津理工大學學報, 2013, 29(5): 16-20.

FAN Jian-hui, ZHAO Xin-hua, LI Bin. Inverse Displacement Kinematics and Workspace Analysis of a Novel 3-DOF Parallel Manipulator[J]. Journal of Tianjin University of Technology, 2013, 29(5): 16-20.

[16] TIAN Chun-xu, FANG Yue-fa, GE Q J. Design and Analysis of a Partially Decoupled Generalized Parallel Mechanism for 3T1R Motion[J]. Mechanism and Machine Theory, 2019, 140: 211-232.

[17] YANG Shuo-fei, SUN Tao, HUANG Tian. Type Synthesis of Parallel Mechanisms Having 3T1R Motion with Variable Rotational Axis[J]. Mechanism and Machine Theory, 2016, 109: 220-230.

[18] DESAI R, MUTHUSWAMY S. A Forward, Inverse Kinematics and Workspace Analysis of 3RPS and 3RPS-R Parallel Manipulators[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2021, 45(1): 115-131.

Design and Workspace Analysis of Parallel Canning Mechanism Based on 2CRU/2PRRR

LIU Jian-guo, MA Chun-sheng, WEN Jie, LI Rui-qin, QU Shu-wei

(School of Mechanical Engineering, North University of China, Taiyuan 030051, China)

The work aims to propose a new 2CRU/2PRRR parallel mechanism to solve the problem that the filling mechanism in current on the assembly line is not suitable for bottles with inclination angle. Firstly, a three-dimensional model of the 2CRU/2PRRR parallel mechanism was created with SolidWorks software. The degree of freedom of the mechanism was analyzed by the screw theory and verified by the modified Kutzbach-Grübler formula. Then the kinematics model and D-H method were used to analyze and solve the inverse position solution of the mechanism moving platform. Finally, the corresponding limit boundary search program was programmed with Matlab software, and the workspace of the mechanism was solved by calculation, and the application example of the filling mechanism in the assembly line was given. The results indicated that 2CRU/2P RRR parallel mechanism had one rotational degree of freedom, three moving degrees of freedom. The shape of the workspace was a regular cube, and the interior was continuous without cavityand singular position. The parallel mechanism has simple structure, operation steadily, high performance, and it can completely meet the requirements of movement and working range when filling bottles with inclination angles on the assembly line, thus improving the versatility of the filling mechanism.

2CRU/2PRRR; parallel mechanism; spiral theory; position inverse; workspace

TB486；TH112

A

1001-3563(2022)07-0184-06

10.19554/j.cnki.1001-3563.2022.07.023

2021-05-19

山西省自然科學基金（201801D121183）；山西省回國留學人員科研資助項目（2021-114）

劉建國（1998—），男，中北大學碩士生，主攻機構理論與機器人技術。

馬春生（1974—），男，博士，中北大學副教授，主要研究方向為機構理論與機器人技術。

責任編輯：曾鈺嬋