基于數據驅動信息技術與課程融合
——以J省初中數學中考為例

江西師范大學新聞與傳播學院 萬文琦 孟曉倩 鄭佳雪 何彤宇

在“互聯網＋”的社會大環境下，各行各業人員都置身于一場大數據驅動的變革中。在教育領域中，大數據對于信息技術與課程的整合有不可忽視的作用。本研究以初中數學為例，運用社會網絡分析法，借助Ucinet、Bibexcel軟件，整理中考數學題目知識點，在網絡科學的角度，從知識點數量、關鍵詞、網絡節點相互影響、知識點考頻發展趨勢方面，對2011年以來對J省中考數學試卷情況進行較為全面的研究與分析。基于分析結果，借助信息技術手段，對促進信息技術與課程融合的實踐提出預想與建議。

大數據指的是基于互聯網等現代飛速發展的科技手段，通過對大量數據進行快速計算和分析，形成有利于決策與發展的參考信息。大數據的“大”就大在對大量數據的收集和分析，不是量的龐大，而是在眾多數據中迅速獲取信息[1]。隨著大數據分析技術的發展，大數據驅動的研究范式已成為教育科學研究的新取向[2]。筆者設想，利用大數據技術對教學內容中客觀存在的各類數據進行采集和分析之后，可以揭示數據中隱含的教學問題，由此助力精準教研。

在《教育信息化十年發展規劃（2010-2020）》中強調要推進信息技術與教學融合。我國在實踐過程中，取得較多成就也面對著較多問題。其中在學科教學內容與信息技術進行整合的過程中，微課、電子題庫是常見的產物，而在其內容編排上，一味地按照課本上的目錄順序進行編排，或借助思維導圖呈現各知識點之間的關聯，幫助學生理解，但是在引導學生自主建構知識的能力，實現精準教學方面仍然存在很大空間。

本文基于大數據驅動研究視角，以J省近9年的中考題作為數據樣本，運用社會網分析和知識可視化等研究方法，以改善課堂教學效率，實現精準教學為目標展開研究。

1 研究設計

社會網絡分析方法（Social Network Analysis，簡稱SNA）近30年來已發展為社會科學研究的一種新范式[2]。像我們平常所說的網絡，社會網絡是由多個節點及節點間的連線組成的集合[3]。節點可以是各種事物，節點間可以通過各種關系聯系起來[3]。其中，社會網特別強調“連接”的重要性。比起節點本身的特征與屬性，社會網認為節點之間的關系、“節點”之間的相互影響對于網絡這個整體更為重要。反之，網絡對節點的影響也需要特別重視，單獨的節點無法看出其影響，只有把節點放入網絡中考查，才能客觀地解釋它。

從社會網絡的視角看，本案例中的數據樣本中考題涉及的各知識點，就是網絡中的各個節點，而它們處于一個網絡中則體現了每個知識點之間的聯系[4]。在知識點的社會網絡中，由于各知識點處于的位置以及共現頻次的不同，每個知識點在網絡中具有不同的地位，重要性也不同。在不同的情況下，有些知識點反映的是某個領域中的長期考核熱點；有些知識點則是處于近期興起的新考法；還有些知識點之間的聯系非常緊密，而有些知識點容易看起來顯得比較孤立，但在網絡中能發現它與其他知識的關聯。

2 數據采集與加工

2.1 數據采集

數據的采集分為四個過程：第一階段：收集2012年至2020年J省中考數學試卷。第二階段：整理每份試卷，并盡可能全地提取每份試卷上所有題目所涉及的知識點。第三階段：根據涉及知識點，利用Bibexcel形成共詞矩陣。第四階段：將共詞矩陣導入Ucient進行社會網絡可視化分析。

本文運用社會網絡分析法，對2011年以來的9份中考數學試卷進行分析，包括所涉及的知識點1076個關鍵詞，在展示初中數學中考考點基本情況的基礎上，揭示知識點各自關聯的特點。

2.2 矩陣構建

在知識點確定后，首先對所有知識點進行編號，依次編號為Z1、Z2、Z3、……Z110；然后分析各知識點的關聯情況，將樣本數據矩陣化，形成一個賦值矩陣。其基本思路是采用n階賦值矩陣S記錄知識點之間的社會網絡（n為網絡節點數）信息方式，S［i，j］是矩陣中的一個元素，表示知識點i與知識點j出現在一道題目中的次數，“0”表示i與j無關聯，數值越大表示聯系越密切。本研究對9年中考試卷所涉及的知識點進行編碼，形成如表1所示的知識聯系矩陣編碼（部分），然后將關系矩陣導入UCINET軟件中進行分析[5]。

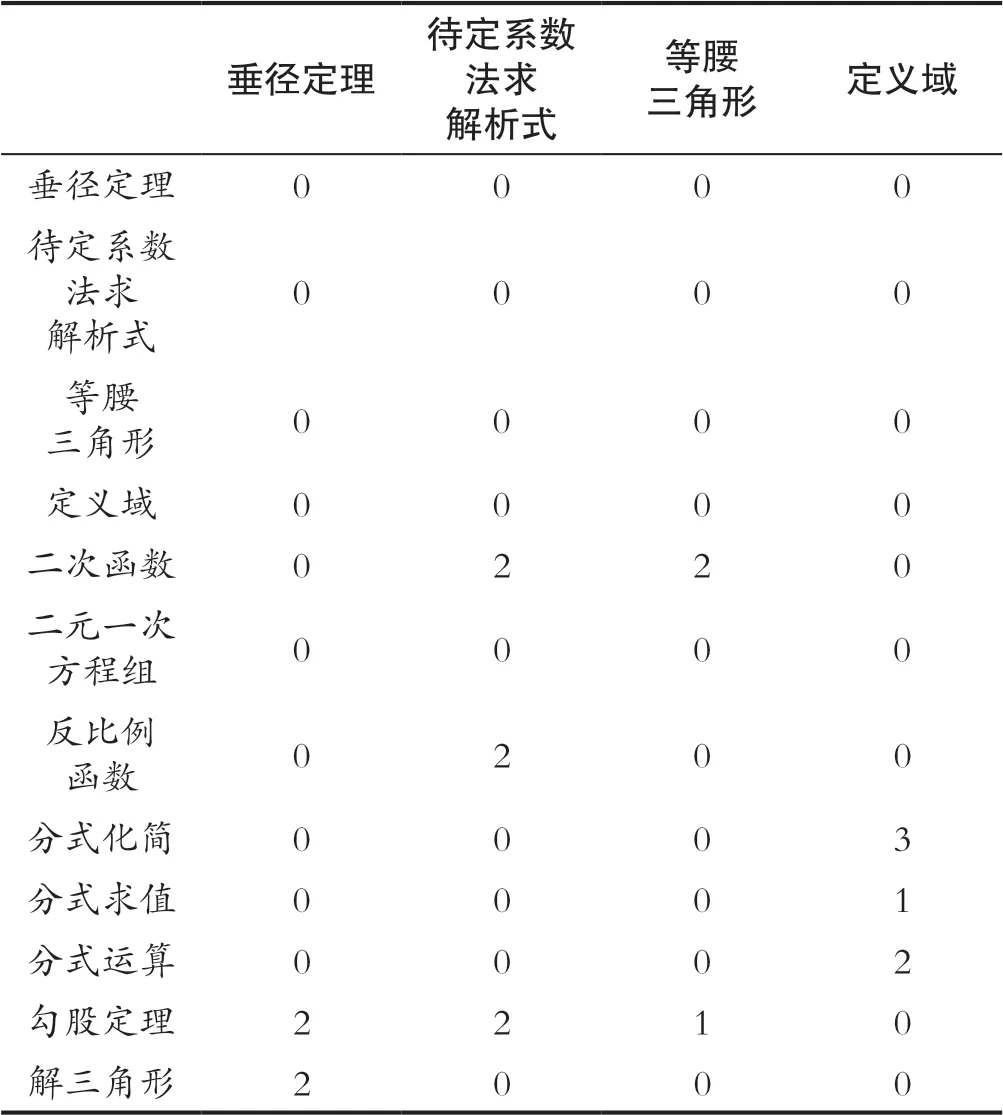
表1 知識點關聯之賦值矩陣（部分）Tab.1 Assignment matrix of knowledge points association (part)

3 社會網絡構建與分析

社會網絡分析法作為社會科學廣泛運用的一種研究方法，已經日趨成熟。本文從網絡中心性、凝聚子群、小團體等角度展開分析與論述。

3.1 社會網的構建

本文運用Ucinet社會網絡分析軟件，對2011—2020年中考數學試卷進行了分析，如表2所示直觀地反映了近幾年中考數學的知識點分布及關聯的整體特征。并以此為基礎，繪制出近9年J省數學中考試卷高頻知識點網絡結構圖（如圖1所示）。

表2 社會網絡的基本屬性Tab.2 Basic attributes of social networks

(1)該網絡是稀疏網絡。網絡密度是衡量社會網絡中各個知識節點之間聯系的緊密程度的重要參數。根據相關理論，網絡密度越大，其中知識點的出現頻率、產生影響的可能性就越大。通過計算可知該網絡由33個知識點形成了150個連接，網絡密度為0.142，即網絡中只有14.2%的連接，顯示此網絡密度較為稀疏。

(2)網絡的凝聚力較高。計算可知網絡的聚類系數為0.678，將高頻知識點關鍵詞的二值化矩陣導入，運用Ucinet進行節點中心度的計算各小組之間的聯系較為緊密。平均距離為1.912，說明網絡中的每一個知識點通過1.912個知識點即可到達另一個知識點，說明這是一個信息流通順暢的網絡。該網絡兩點之間的平均距離為1.794，說明網絡中的每一個知識點通過1.794個知識點即可到達另一個知識點，也從側面反映了該網絡連接緊密。

如圖1所示，該網絡為非完全連通網絡，其中左上角出現由五個知識點組成的子網絡，聯系非常密切，該子網絡代表分子求值、分式運算、分式化簡、定義域和二元一次方程組的融合，這代表了該實驗組在中考試卷研究中一個研究方向。

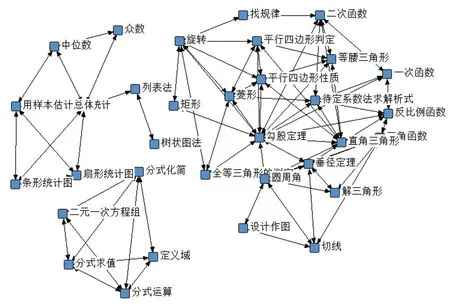
圖1 知識點網絡結構圖Fig.1 Knowledge point network structure diagram

右上角是最大的聯通子網絡，從圖中可看出，勾股定理、平行線、反比例函數、三角函數處于網絡中心位置。一方面，這些知識點出現的頻次較高，說明這些知識點共現次數較多，共線可能性越大，日后放在一起考查的可能性就越高；另一方面，從連線的粗細程度來看，每兩個知識點之間的連線越粗，說明二者的關系越密切，反之越疏遠。例如可以從圖中看到，“設計作圖”雖然處于網絡邊緣，但很有可能將成為未來命題的發展趨勢。

3.2 結果分析與討論

3.2.1 中心度分析

社會網絡分析中，中心性分析是重點。要知曉知識點居于怎樣的中心地位，常常通過中心度分析中的中介中心度、特征向量中心度與度中心度的三個維度來分析。它們既可以反映某個研究領域的當前研究熱點，也能夠預測某研究領域的未來發展趨勢[6]。

(1)度中心度。度中心度是對某個節點在網絡節點中所處地位評價的一項指標。其含義可以理解為：在一個社會網絡中，一個節點與其他節點都存在著的聯系越多，連接其他節點的數量越多，那么就可以理解為這個點在此網絡分布中越接近中心的位置，影響力越高。反映出節點對整個社會網絡影響力的大小，以數據的方式直觀預測出社會網絡的發展動態。

通過對知識點高頻詞匯計算得出節點中心度，如表3（部分）所示，可以發現“勾股定理”處于此關鍵詞網絡的中心地位，絕對中心度數值為14，相對中心度為43.75，這明顯地反映出“勾股定理”與其他關鍵詞之間具有緊密聯系；并且“直角三角形”的絕對中心度為9，“旋轉”“圓周角”的絕對中心度為7，“垂徑定理”“平行四邊形的判定”“二次函數”等7個關鍵詞的絕對中心度為6，這五者的點度中心度在數值上較“勾股定理”偏小，僅剛到其一半，這就說明這些高頻關鍵詞所代表的知識點的考查方向在中學生數學能力考查上可能將會是新的熱點，這些知識點都指向了代數和幾何的整合。通過上述分析，可以看出數形結合的思想正逐漸成為中學生數學能力考查的關鍵領域。

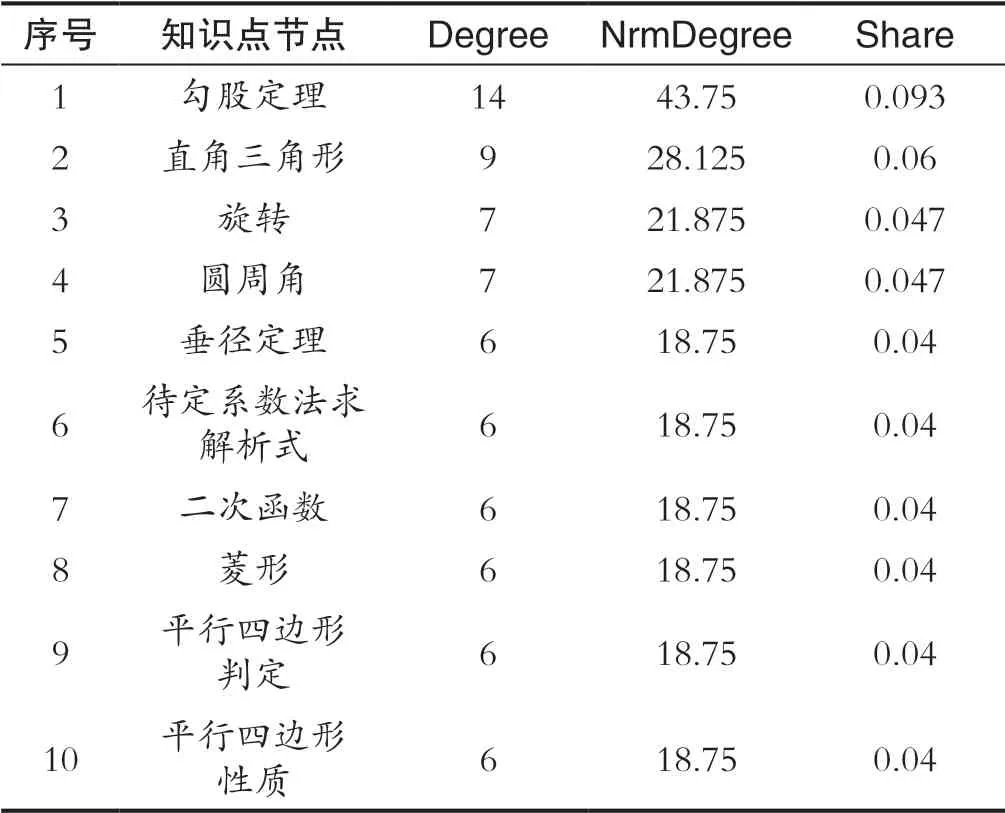
表3 度中心度據部分Tab.3 Center data part

網絡中間中心勢指數為：Network Centralization Index=31.45%，屬于中等水平，說明社區不存在明顯的網絡集中性、向心性。根據表4，可以發現勾股定理、直角三角形、圓周角、旋轉、垂徑定理這些關鍵詞，具有較高的點度中心度，處于網絡的核心位置。與此同時，以上節點具有較高中間中心度，處于網絡中與其他節點關聯的“中間”位置，是連接其他節點的中間橋梁，顯示在整個網絡有較高的影響力以及控制力。

(2)中介中心度。在一個整體網絡上，如果一個點處于許多其他點對的連接路徑上，就說明該點具有較高的中介中心度，即中介中心度能夠表現出節點在整個社會網絡關系中的連通程度。

計算顯示“勾股定理”的中介中心度最高（如表4所示），數值為73.537，相對中介中心度為14.826，“圓周角”的中介中心度暫列第二為31.989，“直角三角形”與“垂徑定理”分別以20.648與16.239位于第三位和第四位。這些數據說明整個數學素養能力考查的過程中，越來越重視“直角三角形”，注重數學知識在生活中的應用。而“反比例函數”“垂徑定理”與“四邊形”在整個數學測試的能力考查中處于基礎知識地位，也是解決大部分題目的思路導向，其中間中心度的數值遠大于其他關鍵詞的數值是正常情況。“樣本估計總體”“待定系數法求解析式”“一次函數”“二次函數”“交點”這6個知識點為中間中心度排行的第6至10位，且其相對中介中心度數值均大于1，這就說明這幾個關鍵詞在數學能力測試的過程中一同出現的頻率較高。結合這5個知識點在網絡圖中所處位置，對未來如何圍繞進一步培養與提升學生數學素養指出了方向。

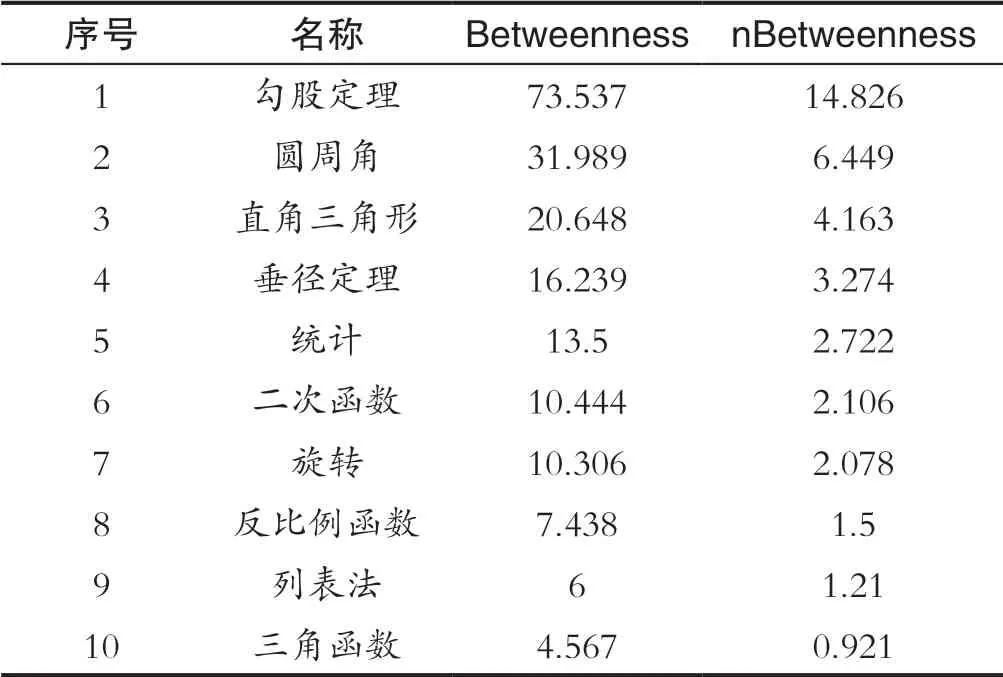
表4 中介中心度（前十名）Tab.4 Intermediary centrality (top 10)

3.2.2 核心-邊緣分析

每年的考試試題都會有知識點的考查變化，因此及時發現并關注知識點的變化是重要任務，而社會網絡分析中的核心—邊緣（Core—Periphery）結構分析根據網絡中結點之間聯系的緊密程度，將網絡中的結點分布分為核心區域和邊緣區域兩種情況。本文根據核心度（Coreness）計算結果，得出知識點分布的兩種情況，其中一類是具有緊密聯系的知識點，可以視為核心知識點，屬于核心位置；另一類是相互間聯系較少的知識點，處于邊緣位置。各關鍵詞的核心度數值如表5所示。

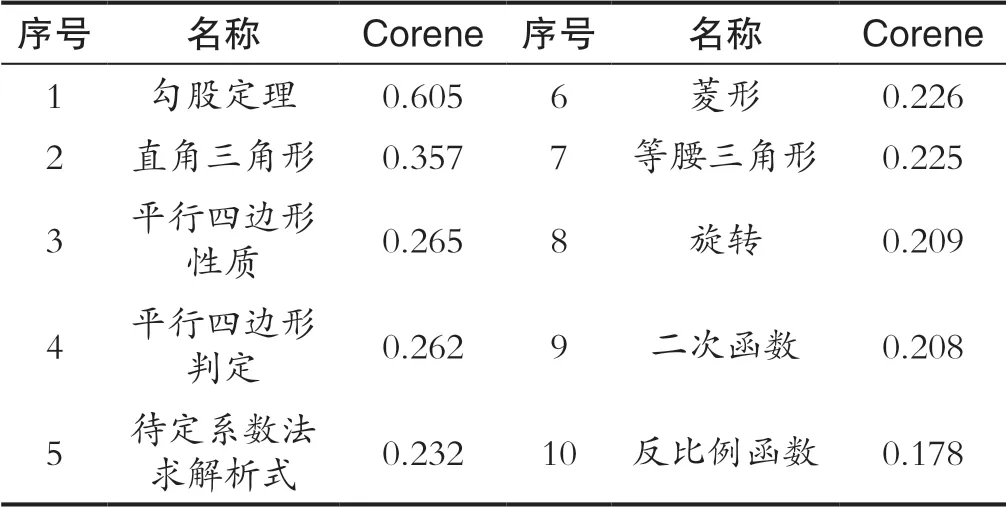
表5 核心度（Coreness）計算結果（前十名）Tab.5 Calculation results of Coreness (top 10)

但是在現實網絡中，成員之間并不一定具備嚴格的量化關系。在本研究中，根據計算結果，將核心度數值以0.05與0.15為臨界值，從低到高，將關鍵詞定義為邊緣、半邊緣以及核心知識節點（如表6所示）[7]。

表6 核心邊緣分類Tab.6 Core edge classification

3.2.3 小團體分析

小團體分析的目的是調查成員之間關系的緊密程度，并從中對形成的網絡進行研究。當網絡中成員之間因為某些方面產生聯系而形成一個小團體時，被稱為凝聚子群。對凝聚子群進行研究與分析，目的是為了揭示網絡中存在的實際或是潛在的關系，由此用以解釋現象或是對未來進行預測。凝聚子群分析中常見的分析類型包括k-叢、k-核、派系、n-派系、n-宗派等[8]。

k-叢是建立在點度數基礎上的，一個k-叢就是滿足下列條件的一個凝聚子集，即在這樣的子群中，每個點都至少與除了k個點之外的其他點直接相連。如圖2所示我們很容易看出各小團體之間的隸屬關系，而顯示構建了108個小團體，并給出了各小團體內部成員構成。結合之前的網絡圖和中心度計算結果，有助于教師把握各知識點之間內在關系，提供精準教學，提升課堂教學質量和效率提供了支撐[9]。

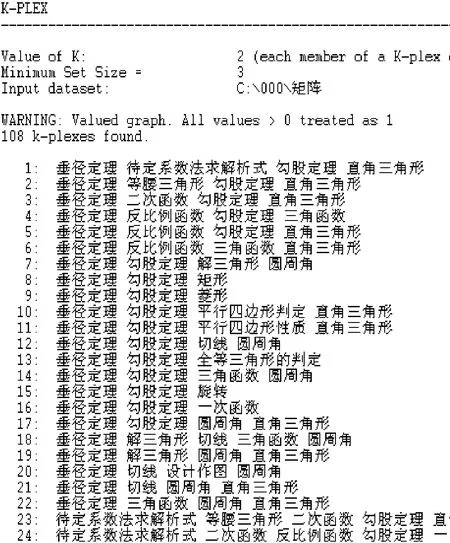
圖2 k-叢成員分析圖（部分）Fig.2 k-cluster et analysis (portion)

經過UCINET分析，可以發現其凝聚子群密度為0.733，接近1，表明該網絡中派系林立的程度較高，各個知識點之間聯系較為緊密（如圖3所示）。

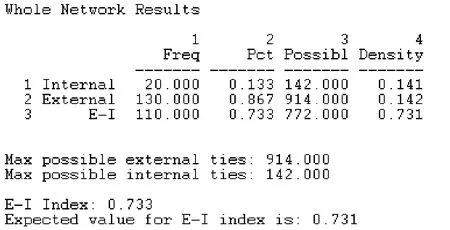
圖3 凝聚子群密度Fig.3 Condensed subgroup density

3.3 數學測試考查熱點主題分析

通過對J省近9年數學學科的普通中等學校招生試卷進行社會網絡分析，可以得到以下三個結論，指向中學學生數學學科素養日后的發展趨勢。

(1)注重實際應用能力在幾何模型中的應用，培養學生在實際中抽象出幾何模型的能力。“勾股定理”其度中心度最高，“實際應用”的中介中心度最高，二者便代表者幾何與實際生活的碰撞與聯系。可以看出數學測試已經不僅僅停留在計算正確與公式應用上了，而需要的是將所學知識應用于解決實際問題上去。學以致用是學生學習的驅動力，只有學生能夠感受到知識的存在意義，了解知識的應用方法，才能以積極主動的態度有效地學習。

(2)注重統計概率中數據分析概念的理解，培養學生隨機性思維能力。數據分析作為研究隨機現象的重要手段，不僅是大數據時代數學應用的主要方法，同時也是培養數學學科核心素養的重要內容之一，其在中考數學中最常見的體現是與統計概率結合。“統計”與“用樣本估計總體”的中介中心度較高，而“用樣本估計總體”便是數據分析預測數據日后走勢的雛形。區別于常見的針對特定題型，利用“思維定式”解題的題型，這樣需要估測，帶有不確定性的問題，相對于利用確定性思維解決問題的想法，統計概率充滿了不確定性，對于學生日后“隨機思維”的訓練是至關重要的。

(3)注重培養學生將表面的代數關系轉化為直觀圖像關系的能力，探究數學問題條件和結論的內在聯系，從而幫助學生構建“數形結合”思想，將抽象的思維轉化為形象的圖形關系而進行解題。在度中心度的分析中，前五項中有三項是“一次函數”“二次函數”與“交點”，三者度中心度較高，可以看出函數、方程、圖形三者的關系的探究在整個中學數學學習中，處于較為重要的地位。

4 建議與對策

本研究選擇中學數學學科作為研究對象，通過對近十年中考試卷的數據分析，從數據驅動視角出發，以精準教學為目的，采用社會網等數據分析方法，力圖促成信息基礎與課程的深度融合，推動教學質量和效率的提升，并取得一定成效。通過實踐和研究，我們未來今后還要在以下幾個方面進一步展開深入研究。

隨著大數據技術在教育領域中的廣泛深入應用，應該怎樣獲取、搜集數據，如何挖掘數據中的隱藏的信息，如何將數據整理歸納成我們需要的信息，從而促進教學，提升教學效率，進而改進教學，是教育與大數據融合發展的意義。

(1)注重教師數據素養的提升。教師作為教學改革的源動力和創新者，要求教師不僅對數據具備敏銳的觀察和判斷力，同時要求能夠在日常教學過程中熟練運用相關工具，對數據進行采集并進行科學地歸納、分析和整合以支持教學。不僅是教學內容上的大量數據，包括在教學活動開始時、教學過程中、教學活動結束后的反思自省階段，教師可以嘗試利用荷蘭博爾赫斯提出的知識測試類工具，參考艾波拉的數據決策模型進行數據的收集處理及加工，進而實現支持教學的目的。

(2)基于數據驅動的教學改革前提是數據真實可靠。隨著數據規模日益龐大，對數據的質量也提出了更高的要求。針對當前教育數據來源分散、利用率低下的問題，相關管理者需根據教育數據特點，數據的發現、采集、存儲、分析等環節進行優化和規范，完善數據原始加工和整合，保證數據的科學性、規范性和系統性，為大數據驅動教學改革和創新提供堅實基礎[10]。