基于d-正則(3,2s)-CNF問題的加密方案*
上饒師范學院 孫瑞
本文旨在d-正則(3,2s)-CNF問題基礎上提出公鑰加密系統,但一般的具有正則結構的SAT合取范式并沒有加密作用,因此給研究過程帶來較大障礙。為了解決此類問題,我們結合并改進SDRRK2S模型作為隱藏明文的工具,通過引入此模型生成難解的d-正則(3,2s) -CNF實例,可以達到密文合取范式難解的目的,從而提高其安全性。
1 研究背景
公鑰加密體制是現代網絡信息安全的重要工具,也是后量子時代密碼學中的關鍵技術,它們建立在某些難解問題的基礎上來確保加密體制的安全性,較對稱密碼系統安全程度更高,公鑰加密模型如圖1所示。而d-正則(3,2s)-CNF問題是相對于其他問題假設來說應用在密碼方案里極少的類型,目前的基于SAT構造的加密系統[1]安全程度較低。值得關注的是,布爾合取范式的臨界值影響了其是否可滿足性與求解難度,在此方面的研究更多的是關注其參數與求解難度間的關系。研究者們通過矩方法等得出了隨機(k,s)-SAT臨界值的范圍[2-6]。而后,人們提出的d-正則(3,2s)-CNF問題是一個具有更強正則約束的SAT問題,而2020年符祖峰等人[7]證明了構造此類難解實例的參數范圍,并給出了SDRRK2S實例生成模型,這對我們進一步加強基于SAT問題密碼方案的安全性帶來了有力工具。受此啟發,下面我們以這些研究工作為基礎來建立一個以d-正則(3,2s)-CNF問題為困難性假設的加密模型。
2 方案介紹
在本節,將闡述此加密算法的具體過程,加密系統模型如圖2所示。

圖2 本方案加密算法模型Fig.2 The encryption algorithm model of this scheme
算法1:密鑰生成算法
Input:隨機選擇變量個數M,以及n,yj(j=1,2,...,M),出現的次數2s=20,d=8(其中n,M∈N*,M≥220,n/M=4.267,sM=3n,),私鑰sk:Y=y1y2...yM,k=3。
Output:d-正則(3, 2s)-CNF公式
Step 1.令R:=?,t:=1,E:=1,K=1,2,...,N,保存E中值為真的文字序號;
Step 2.對于每個yj(j=1,2,...,M),將yj的(或)個正文字和(或個負文字置于B中;
Step 3.在B中任意不重復地抽3個文字ek1,ek2,ek3;
Step 3.1如果t≤n,E=1時,重復下列步驟;
Step 3.2如果k1、k2、k3兩兩互不相同,且ek1,ek2,ek3互異且不同時出現在已產生的Et中,(令t=1,2,...,n,表示的真值),執行Step 3.2.1和Step 3.2.2;
Step 3.2.1 把ykj代 入ekj( j∈{1, 2, 3}),如果將ekj置于B中,同時把kj置于S1;否則,執行Step 3.2.2;
Step 3.2.2 核對已產生的含有kj(j∈{1,2,3})的Sk(k=1,2,...,t-1),如果將ykj的值代入Ek后,所對應的ek′j真值為1,同時Ek里另外三個文字被私鑰賦值后任意一個真值為1,則互換ekj與ek′j,并把kj放置于St內,再把Sk里的kj去除;否則,把ek1,ek2,ek3置于B內,執行Step 3;
Step 3.3得到析取范式Et,把里面的ek1,ek2,ek3按角標依次增大排列;
Step 3.4R:=R∩Et,t:=t+1,E=1,那么執行Step 3;
算法2:加密算法
算法2.2 產生布爾函數,它是由除Et中出現的變元外的其余變量構成的任意布爾函數;
算法2.3 假設明文是X,通過運算下列式子加密:

為使上式成立,作如下分類討論:
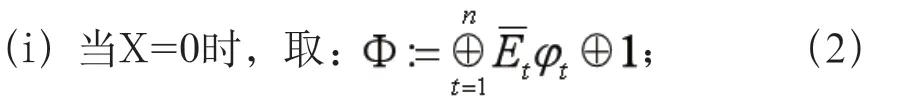
算法3:解密算法
接收者使用私鑰Y=y1y2...yM計算密文:X=Φ⊕1,解出X。
3 方案分析
3.1 正確性分析
我們通過明文的兩種取值來討論方案的正確性:
即:X⊕Φ=1
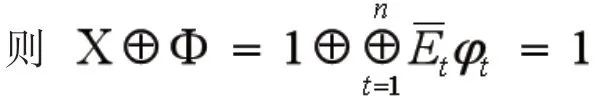
所以,(1)式是正確的。
3.2 方案對比
下面我們將本方案與文獻[1]的加密系統進行對比,具體將從困難性假設與安全性兩方面討論。如表1所示:

表1 本文方案與已有的基于SAT的加密方案的對比Tab.1 Comparison between the proposed scheme and existing SAT-based encryption schemes
由上表可知,文獻[1]是建立在k-SAT問題基礎上的,而我們的方案是基于隨機正則d-正則(3,2s)-CNF問題的難解性假設。兩個方案在密鑰長度和密文的長度上相同,但本方案是IND-CPA安全的,相對來說能夠提供更高的安全保障。
4 結語
本文在傳統的3-SAT問題上另辟蹊徑,在隨機d-正則(3,2s)-CNF問題的基礎上構造了加密協議。相比方案[1],本文結合了SDRRK2S模型,同時將約束密度控制在了使得d-正則(3,2s)-CNF難以求解的值上,進一步強化了加密算法的安全程度,相對于現有的基于SAT問題的密碼系統安全系數有所提高。但目前仍然存在加密效率不高,以及安全性還待提高等問題,考慮如何用其他密碼學或數學工具進一步完善是主要難題,接下來的工作方向是如何在保證已有優勢的條件下,使其具有高效、安全以及同態性等較好的計算性質。

