政府監管下煤炭企業綠色開采策略的演化博弈

馬彥敏，李恩平

(太原理工大學經濟管理學院，山西 晉中 030600)

煤炭作為中國的基礎能源，對于支撐國民經濟的發展發揮著重要的作用，但是傳統的煤炭開采方式經常會引發地表坍塌、污染周邊水資源、破壞土地資源等一系列生態環境問題。目前，“2030年前碳排放達到峰值、2060年前實現碳中和”已成為我國的目標，在這一愿景下，煤炭企業應該由傳統以環境為代價的開采方式轉變為綠色、低碳的開采方式，以實現煤炭行業的可持續發展。綠色開采是指在煤炭的生產、銷售過程中，煤炭企業始終貫徹綠色發展理念，尤其是在生產過程中企業能夠主動選擇執行綠色開采技術，提高開采效率[1-2]。綠色開采技術的執行需要煤炭企業進行一定的成本投入，而企業出于自身利潤最大化的考慮，積極主動性會減弱。政府作為煤炭企業綠色開采的監管者，有責任通過給予補貼或實施懲罰來提高煤炭企業執行綠色開采技術的積極性[3]，促使煤炭企業走上綠色開采的路徑。

政府對煤炭企業監管的過程實質上是博弈的過程，學者們運用靜態博弈和動態博弈的方法分別進行了研究。在靜態博弈方面，呂雁琴等[4]通過分析政府和煤炭企業在生態補償問題上的博弈行為，為新疆煤炭資源開發生態補償機制提出了建議；徐水太等[5]研究了礦山企業如何通過與政府博弈，最終積極主動地發展綠色循環經濟。在動態博弈方面，馬媛等[6]、張偉等[7]通過建立政府和煤炭企業的演化博弈模型，從動態的角度探討兩個群體綠色開采監管的演化穩定策略。但是多數研究都是以政府和單一的煤炭企業作為博弈主體，有關政府和兩個大型煤炭企業進行三方博弈的研究較為缺乏。因此，本文通過構建煤炭企業A、煤炭企業B以及政府綠色開采監管策略的演化博弈模型，探討三方主體在動態博弈后的穩定策略，并用MATLAB數值仿真分析促使系統達到最優策略狀態的因素，進而為煤炭企業的綠色開采提出建議。

1 基本假設與模型構建

1.1 基本假設

本文的研究主體為煤炭企業A、煤炭企業B和政府。根據演化博弈理論[8]，博弈參與方都是有限理性的，需要通過不斷的學習、改進來接近最優策略，而不是在最開始就找到最優策略，因此為研究煤炭企業A、煤炭企業B和政府在不同策略組合下的成本、收益以及損失，需作出如下假設。

假設1：博弈的參與者包括煤炭企業A(m)、煤炭企業B(r)、政府(t)，并且在博弈過程中三方群體都是有限理性的，即以自身利潤最大化為目標。

假設2：煤炭企業A和煤炭企業B為當地的兩家大型煤炭企業，它們為了完成政府下達的指標，會存在相互搭便車的行為。

假設3：煤炭企業A的行為策略空間為執行綠色開采技術和不執行綠色開采技術(簡記為M,NM)；煤炭企業B的行為策略空間為執行綠色開采技術和不執行綠色開采技術(簡記為R,NR)；政府的行為策略空間為監管和不監管(簡記為T,NT)。

假設4：煤炭企業A執行綠色開采技術的概率為x，不執行綠色開采技術的概率為1-x；煤炭企業B執行綠色開采技術的概率y，不執行綠色開采技術的概率為1-y；政府監管的概率為z，不監管的概率為1-z。

根據上述假設，需設置相關變量(表1)。不失一般性，假設各變量均大于0。

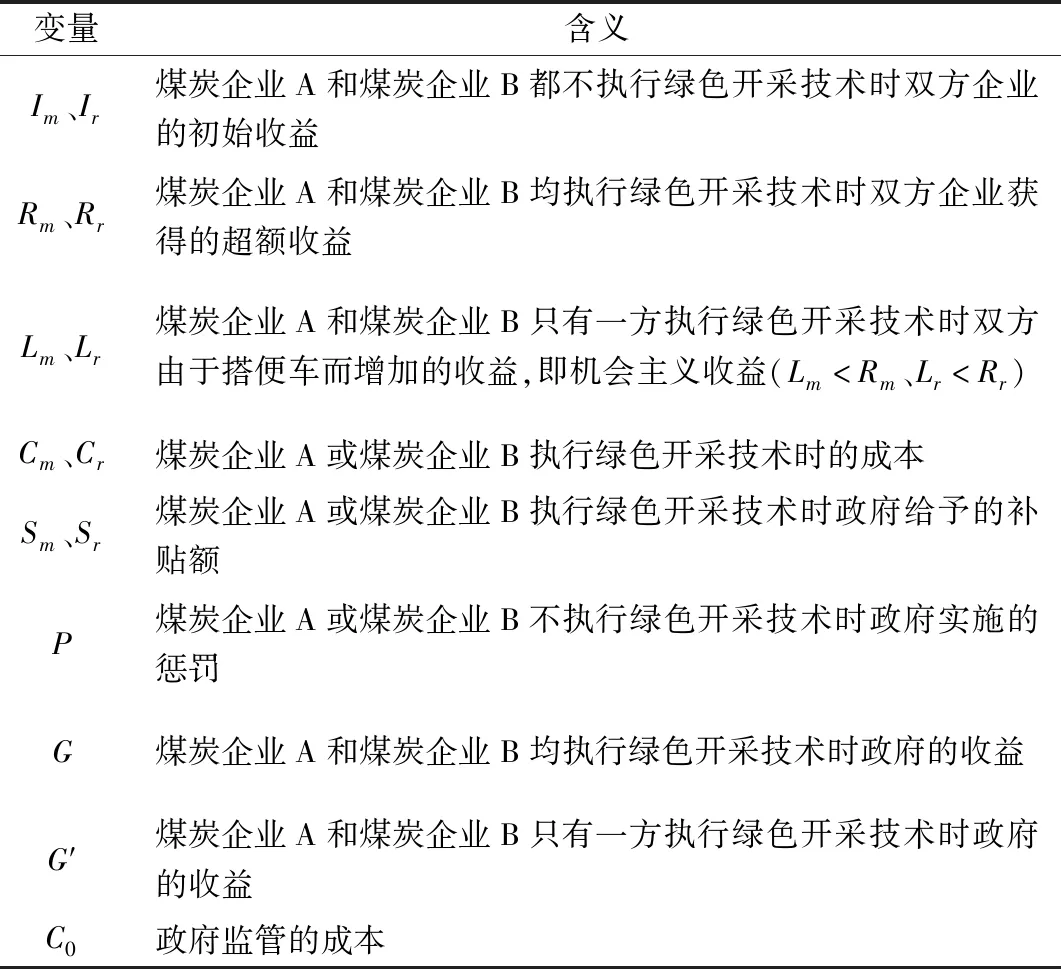
表1 變量設置Table 1 Variable settings

1.2 演化博弈模型構建

根據上述假設和變量，可以得到煤炭企業A、煤炭企業B、政府在選擇不同策略時的收益矩陣，見表2。

表2 煤炭企業A、煤炭企業B和政府三方博弈的收益矩陣Table 2 The income matrix of the tripartite game among coal enterprise A,coal enterprise B and the government

2 模型求解與分析

在模型構建的基礎上，首先求解出煤炭企業A、煤炭企業B和政府的復制動態方程，然后通過雅可比矩陣分析三方綠色開采監管策略的演化穩定性。

2.1 演化博弈模型求解

根據表1和表2可知，煤炭企業A在博弈時執行綠色開采技術的期望收益、不執行綠色開采技術的期望收益、平均期望收益計算分別見式(1)～式(3)。

EM=zy(Im+Rm+Sm-Cm)+

z(1-y)(Im+Sm-Cm)+

(1-z)y(Im+Rm-Cm)+

(1-z)(1-y)(Im-Cm)=

yRm+zSm+Im-Cm

(1)

ENM=zy(Im+Lm-P)+

z(1-y)(Im-P)+(1-z)y(Im+Lm)+

(1-z)(1-y)Im=yLm-zP+Im

(2)

x(yRm+zSm+Im-Cm)+

(1-x)(yLm-zP+Im)

(3)

由演化博弈理論可知，煤炭企業A的復制動態方程為式(4)。

x(1-x)[y(Rm-Lm)+z(Sm+P)-Cm]

(4)

煤炭企業B在博弈時執行綠色開采技術的期望收益、不執行綠色開采技術的期望收益、平均期望收益計算分別見式(5)～式(7)。

ER=zx(Ir+Rr+Sr-Cr)+

z(1-x)(Ir+Sr-Cr)+(1-z)x(Ir+Rr-Cr)+

(1-z)(1-x)(Ir-Cr)=xRr+zSr+Ir-Cr

(5)

ENR=zx(Ir+Lr-P)+z(1-x)(Ir-P)+

(1-z)x(Ir+Lr)+(1-z)(1-x)Ir=

xLr-zP+Ir

(6)

y(xRr+zSr+Ir-Cr)+(1-y)(xLr-zP+Ir)

(7)

則煤炭企業B的復制動態方程為式(8)。

y(1-y)[x(Rr-Lr)+z(Sr+P)-Cr]

(8)

政府在博弈時監管的期望收益、不監管的期望收益、平均期望收益計算分別見式(9)～式(11)。

ET=xy(G-C0)+x(1-y)(G′-C0)+

(1-x)y(G′-C0)+(1-x)(1-y)(-C0)=

xy(G-2G′)+xG′+yG′-C0

(9)

ENT=xyG+x(1-y)G′+(1-x)yG′=

xy(G-2G′)+xG′+yG′

(10)

z[xy(G-2G′)+xG′+yG′-C0]+

(1-z)[xy(G-2G′)+xG′+yG′]

(11)

則政府的復制動態方程為式(12)。

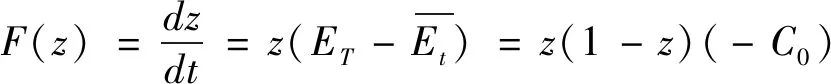
(12)

將式(4)、式(8)和式(12)聯立，得到煤炭企業A、煤炭企業B、政府的復制動力系統，見式(13)。

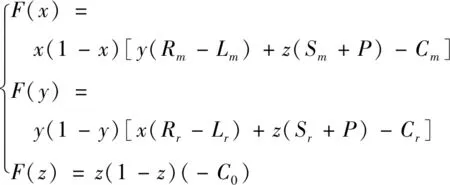
(13)

令F(x)=F(y)=F(z)=0，可以得到局部均衡點。多群體演化博弈的演化穩定點(ESS)必然為純策略納什均衡，即在非對稱博弈中混合策略均衡一定不是演化穩定均衡[9]。因此，后續研究僅需要分析8個純策略均衡點，即E1(0,0,0)，E2(0,0,1)，E3(0,1,0)，E4(0,1,1)，E5(1,0,0)，E6(1,0,1)，E7(1,1,0)，E8(1,1,1)。

2.2 演化博弈模型分析

FRIEDMAN[10]提出，通過分析復制動力系統所對應雅可比矩陣的局部穩定性，可以得到該系統的演化穩定策略(ESS)，而雅可比矩陣見式(14)。

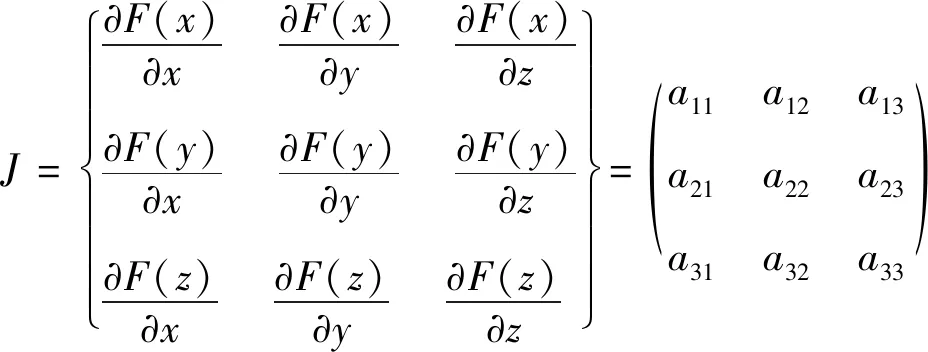
(14)

由式(13)和式(14)可知，煤炭企業A、煤炭企業B、政府復制動力系統的雅可比矩陣見式(15)。

因此，雅可比矩陣J的特征值分別為：λ1=(1-2x)[y(Rm-Lm)+z(Sm+P)-Cm]，λ2=(1-2y)[x(Rr-Lr)+z(Sr+P)-Cr]，λ3=(1-2z)(-C0)。依此類推，分別將8個純策略均衡點代入式(15)中，可以得到各均衡點的特征值。根據李雅普諾夫判別法[11]，如果雅可比矩陣中某均衡點的所有特征值λ>0，則稱該均衡點為源，即為不穩定點；如果某均衡點的所有特征值λ<0，則稱該均衡點為匯，即為漸近穩定點(ESS)；如果某均衡點的特征值λ有正有負，則稱該均衡點為鞍，即為不穩定點。因此分別對8個純策略均衡點進行穩定性分析，見表3。

表3 均衡點的穩定性分析Table 3 Stability analysis of equilibrium point

根據表3，分兩種情形對演化穩定策略進行討論。

情形1：當Ri-Li>Ci(i=m,r)時，即煤炭企業A或煤炭企業B的超額收益與機會主義收益之差大于雙方企業執行綠色開采技術的成本，均衡點E1(0,0,0)和E7(1,1,0)的所有特征值均小于0，即該系統有(0,0,0)和(1,1,0)兩個演化穩定點，分別表示煤炭企業A和煤炭企業B均選擇不執行綠色開采技術、政府選擇不監管以及煤炭企業A和煤炭企業B均選擇執行綠色開采技術、政府選擇不監管。

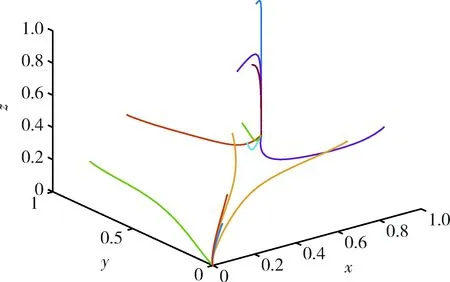
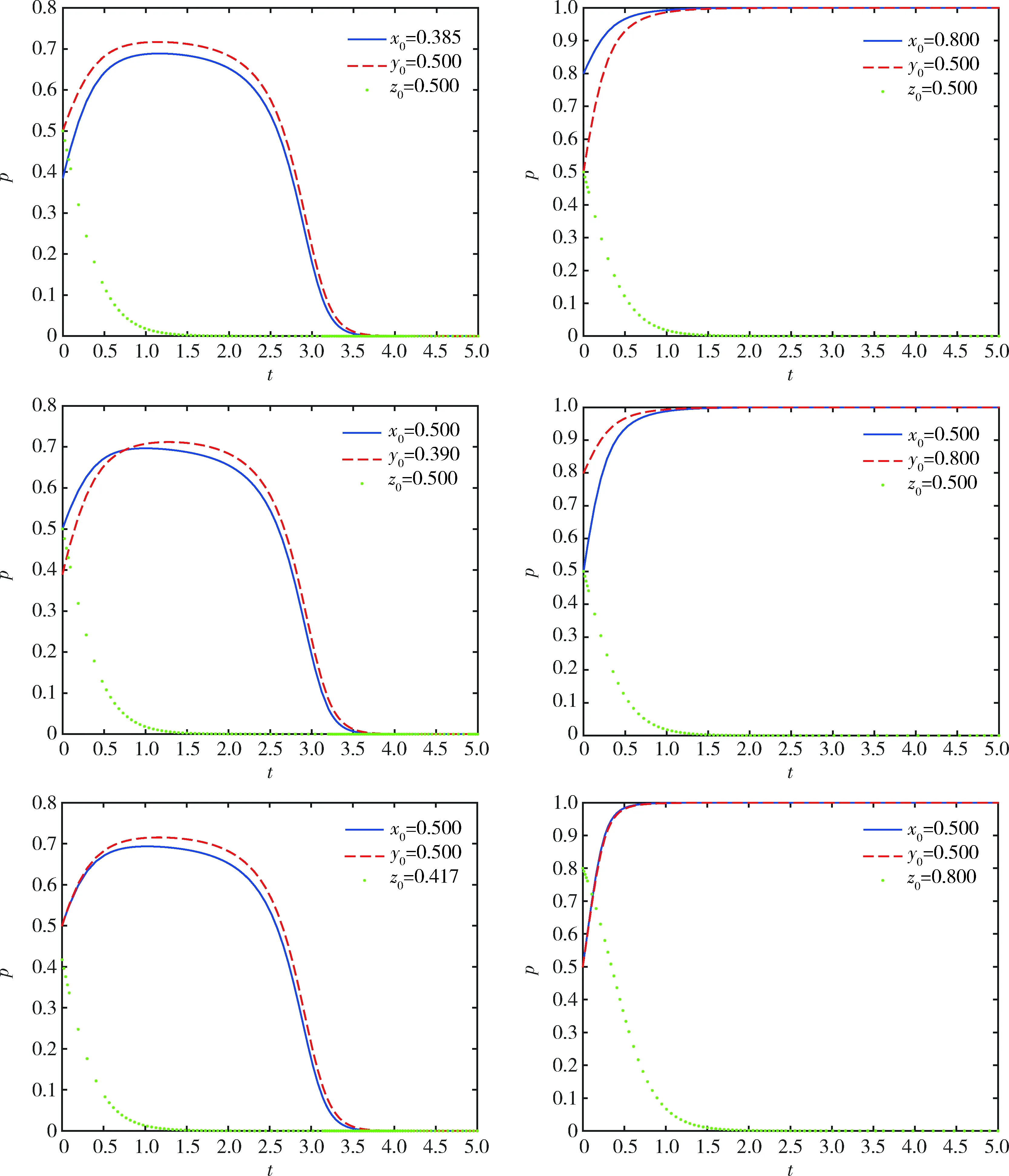
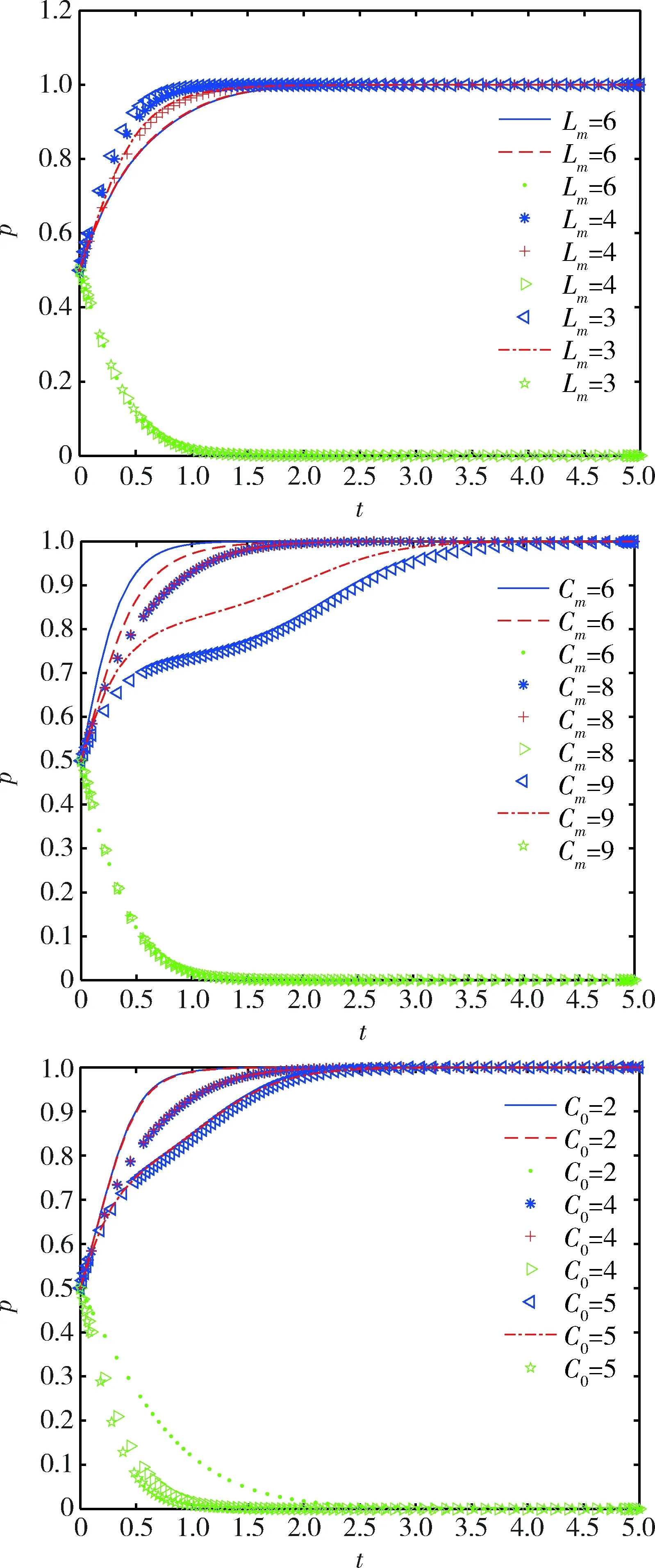
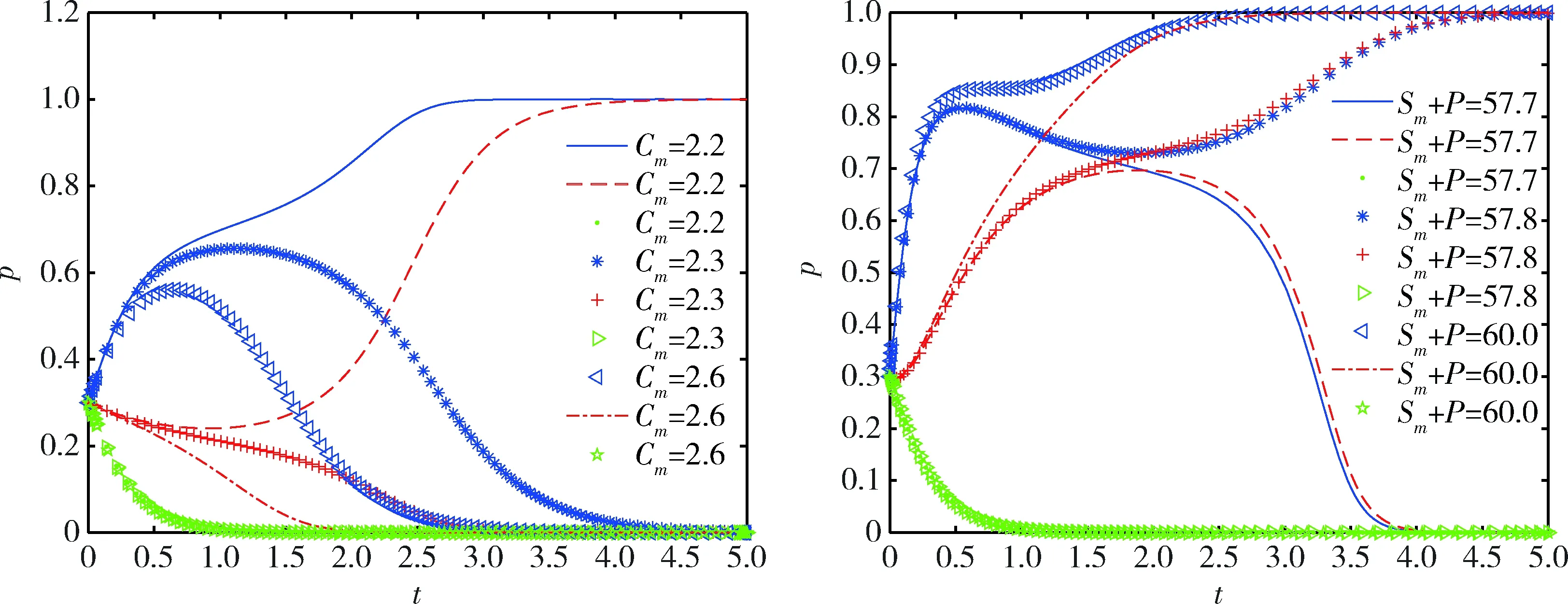
情形2：當Ri-Li

綜上可知，經過一段時間的三方博弈，煤炭企業A和煤炭企業B最終的穩定策略可能是均執行綠色開采技術，也可能是均不執行綠色開采技術，而政府最終的穩定策略是不監管，即對雙方是否執行綠色開采技術無作為。但是本文致力于提供煤炭企業A執行綠色開采技術、煤炭企業B執行綠色開采技術、政府不監管的發展模式，即鼓勵達到(x=1,y=1,z=0)的理想策略狀態，因此下文僅分析Ri-Li>Ci(i=m,r)的情形。

3 數值仿真與分析

3.1 數值仿真

為了驗證當Ri-Li>Ci(i=m,r)時，煤炭企業A、煤炭企業B、政府三方的演化穩定策略以及分析相關參數對演化結果的影響，采用MATLAB2018a軟件進行數值仿真及分析。本文相關參數值根據文獻[12]、文獻[13]和有關專家的意見設置，并且滿足“Ri-Li>Ci(i=m,r)”的限制條件。因此各參數初始值的設置分別為：Rm=17，Rr=14，Lm=6，Lr=4，Cm=8，Cr=7，Sm=9，Sr=8，P=3，C0=4，t=100。在三維空間上描述不同初始點向均衡點演化的過程，演化路徑如圖1所示。結果表明，當煤炭企業A或煤炭企業B的超額收益與機會主義收益之差大于雙方執行綠色開采技術的成本時，系統最終趨向于均衡點(0,0,0)和(1,1,0)，即該系統有兩個演化穩定策略(煤炭企業A和煤炭企業B均不執行綠色開采技術、政府不監管以及煤炭企業A和煤炭企業B均執行綠色開采技術、政府不監管)，該數值仿真也符合雅可比矩陣穩定性分析的結果。

圖1 不同初始點的動態演化路徑Fig.1 The dynamic evolution path of different initial points

3.2 數值分析

由于本文將煤炭企業A、煤炭企業B以及政府看作一個博弈系統，而煤炭企業A和煤炭企業B在演化過程中穩定狀態的形成具有相似性，因此僅對三方主體初始意愿、煤炭企業A的機會主義收益、執行綠色開采技術的成本，政府監管成本以及政府獎懲對系統演化結果的影響進行分析。

3.2.1 初始意愿對系統演化結果的影響

初始意愿對系統演化結果的影響如圖2所示。從圖2可以看出,當煤炭企業或政府的初始意愿較低時，系統最終趨向于均衡點(0,0,0)，即煤炭企業A和煤炭企業B均選擇不執行綠色開采技術、政府選擇不監管；當煤炭企業或政府的初始意愿較高時，系統最終趨向于均衡點(1,1,0)，即煤炭企業A和煤炭企業B均選擇執行綠色開采技術、政府選擇不監管。

圖2 初始意愿對系統演化結果的影響Fig.2 The influence of initial intention on the system evolution results

3.2.2 相關參數對系統演化結果的影響

1)初始意愿均為0.5時分為兩種情況，具體如下所述。

①Lm、Cm、C0對系統演化結果的影響。在初始意愿不變的前提下，分別取Lm=6,4,3、Cm=6,8,9、C0=2,4,5，演化路徑如圖3所示。結果表明：當Rm-Lm>Cm時，即煤炭企業A的超額收益與機會主義收益之差可以彌補其執行綠色開采技術的成本，煤炭企業A為了自身利潤的最大化，最終會選擇執行綠色開采技術。煤炭企業B由于和煤炭企業A在演化過程中穩定狀態的形成具有相似性，最終也會選擇執行綠色開采技術。由于煤炭企業A和煤炭企業B均自主執行綠色開采技術，則政府的監管概率會逐漸降低，最終會對雙方企業無作為。因此，系統最終趨向于均衡點(1,1,0)，并且機會主義收益越小、執行綠色開采技術的成本越小，系統趨向于(1,1,0)的速度越快，進而越能提高煤炭企業A和煤炭企業B執行綠色開采技術的意愿。

圖3 各參數對系統演化結果的影響Fig.3 The influence of various parameters on the system evolution results

當C0分別取2,4,5時，政府選擇監管將產生一定的成本，此時煤炭企業A和煤炭企業B會通過更新設備等措施來避免政府的懲罰，則之后雙方會趨向于自發地執行綠色開采技術，政府也趨向于不監管。因此，系統最終趨向于均衡點(1,1,0)，并且政府監管成本越小，系統趨向于(1,1,0)的速度越快，進而越能提高煤炭企業A和煤炭企業B執行綠色開采技術的意愿。

②Sm+P對系統演化結果的影響。在初始意愿不變的前提下，分別取Sm+P=7.2,7.3,12,16,20，演化路徑如圖4所示。結果表明：當Sm+P為7.2時，政府給予煤炭企業A的獎懲較低，由于企業群體是有限理性的，所以煤炭企業A執行綠色開采技術的意愿較低，煤炭企業B執行綠色開采技術的意愿也較低，則系統最終趨向于均衡點(0,0,0)；當Sm+P為7.3,12,16,20時，煤炭企業A和煤炭企業B執行綠色開采技術的意愿均會增加，雙方之后便會趨向于自發地執行綠色開采技術，政府也趨向于不監管，則系統最終趨向于均衡點(1,1,0)。總之，隨著政府獎懲取值的變化，系統會出現兩個演化均衡點(0,0,0)和(1,1,0)，但是政府獎懲存在一個臨界值(7.2～7.3)，當實際值大于該臨界值時，系統會向(1,1,0)演化，并且實際值越大，系統趨向于(1,1,0)的速度越快，進而越能提高煤炭企業A和煤炭企業B執行綠色開采技術的意愿。

圖4 政府獎懲對系統演化結果的影響Fig.4 The influence of government rewards and punishments on the system evolution results

2)初始意愿較低時。當煤炭企業A、煤炭企業B以及政府的初始意愿均較低時，經過研究發現，Cm、Sm+P有助于系統向理想狀態轉變，演化路徑如圖5所示。結果表明：Cm的取值范圍為2.2～2.6，并且Cm存在一個臨界值(2.2～2.3)，當實際值小于該臨界值時，會使煤炭企業A、煤炭企業B由不執行綠色開采技術轉變為自發地執行綠色開采技術；Sm+P的取值范圍為>57.7，并且政府獎懲存在一個臨界值(57.7～57.8)，當實際值大于該臨界值時，會使煤炭企業A、煤炭企業B由不執行綠色開采技術轉變為自發地執行綠色開采技術。

圖5 Cm、Sm+P對系統演化結果的影響Fig.5 The influence of Cm and Sm+P on the system evolution results

3)初始意愿較高時。當煤炭企業A、煤炭企業B和政府的初始意愿均較高時，Lm、Cm、C0、Sm+P等參數對系統演化結果的影響小于初始意愿對系統演化結果的影響，具體如圖2所示。

4 結論與建議

本文基于演化博弈理論研究了煤炭企業A、煤炭企業B和政府綠色開采監管策略的變化過程，結果表明：煤炭企業A和煤炭企業B由均不執行綠色開采技術轉變為自發地執行綠色開采技術受到初始意愿、機會主義收益、執行綠色開采技術的成本、政府監管成本以及政府獎懲的影響。具體而言：當三方主體的初始意愿為中立時，機會主義收益、執行綠色開采技術成本、政府監管成本的降低會促使系統達到煤炭企業A和煤炭企業B均執行綠色開采技術、政府不監管的狀態，政府獎懲在滿足特定條件時會促使系統達到最優策略狀態；當三方主體的初始意愿較低時，執行綠色開采技術成本、政府獎懲在滿足特定條件時會促使系統達到最優策略狀態；三方主體較高的初始意愿也有助于系統向理想狀態演化。針對結論，本文提出如下建議。

1)有效降低煤炭企業A和煤炭企業B的機會主義收益以及執行綠色開采技術的成本。在執行綠色開采技術的過程中，煤炭企業A和煤炭企業B可能會相互搭便車，這將阻礙雙方綠色開采行為的有效進行，因此，應該建立有效的溝通機制，加強雙方的信任關系，降低機會主義收益；同時，煤炭企業A和煤炭企業B通過掌握關鍵的綠色開采技術、靈活運用綠色開采優惠政策以及加強技術人員的培訓等措施來降低成本投入，促使雙方企業均執行綠色開采技術。

2)降低政府的監管成本。政府監管成本過高會削弱政府的監管力度，這將直接影響煤炭企業的綠色開采行為。因此可以通過精簡監管機構以使各機構之間權責分明、確保政府人員正確合理地運用經濟管理權、引入第三方檢查機制等措施來降低政府部門的監管成本，提升煤炭企業A和煤炭企業B執行綠色開采技術的意愿，促使雙方企業均執行綠色開采技術。

3)完善政府獎懲政策。政府作為監管者，對煤炭企業A和煤炭企業B補貼、懲罰的程度會直接影響雙方企業的綠色開采行為。因此，可以通過加大政府監管力度精準地進行補貼和懲罰，如政府可以根據煤炭企業執行綠色開采技術程度的不同給予差異化獎勵，以使政府的獎懲政策更加完善，從而更好地引導煤炭企業A和煤炭企業B執行綠色開采技術。