次可加勢函數拓撲壓及因子映射

王威 高曉燕

(1.南通理工學院基礎教學學院,南通,226002?2.南京師范大學數學科學學院,南京,210023)

1 引言

拓撲壓是遍歷論和動力系統研究的重點和熱點.1973 年,Bowen[1]在度量空間中定義對于擴張映射的可加勢函數的拓撲壓,證明了拓撲壓的變分原理.1975 年,Walters[2]在度量空間中得到了對于一般連續映射的可加勢函數的拓撲壓的變分原理.1988 年,Falconer[3]考慮次可加勢函數在混合排斥集上的熱力學形式,說明了如何用次可加勢函數來研究非共形變換的動力學.2008 年,Cao[4]把Bowen[1]和Walters[2]的結果推廣到一般緊致動力系統的次可加勢函數上,給出了次可加勢函數的拓撲壓和變分原理.2020 年,Liang[5]利用因子映射給出了一個關于局部化拓撲壓的半共軛公式.1958 年,Kolomogorov[6]引入了經典的測度熵和拓撲熵,之后,熵的研究便成了拓撲動力系統研究的的基本內容.

本文在Zhao[7]研究的次可加拓撲壓的基礎上引入因子映射,給出次可加勢函數拓撲壓的一個上界估計.

定義1([7]) 設(X,d)是緊致度量空間,T:X →X是連續映射,K ?X且K/=φ.對給定的常數ε ＞0,n ∈N,X的子集F稱為X關于T的(n,ε)-生成集,若?x ∈X,存在y ∈F,使得dn(x,y)≤ε,其中dn(x,y)=max{d(Tkx,Tky):k=1,2,···,n-1},X的子集E稱為X關于T的(n,ε)-分離集,若?x,y ∈E,x/=y,有dn(x,y)＞ε.

記rn(d,T,ε,K)為K的(n,ε)-生成集的最小基數,sn(d,T,ε,K)為K的(n,ε)-分離集的最大基數.定義

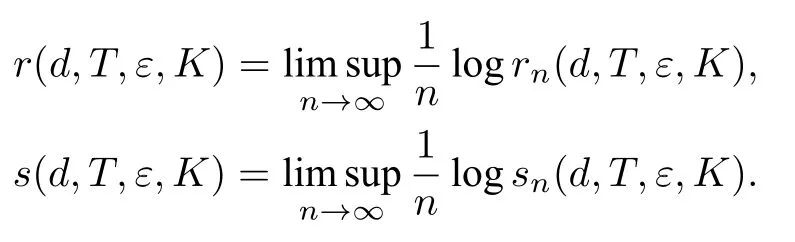
顯然,r(d,T,ε,K)和s(d,T,ε,K)隨著ε的減小而增大.令

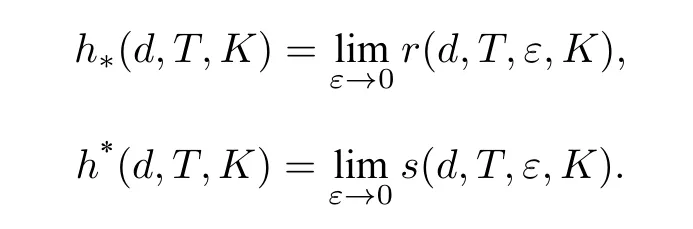
易證h*(d,T,K)=h*(d,T,K)且與X上的度量無關,簡記其為h(T,K),并稱其為非緊集K上的Bowen 拓撲熵.

定義2([7])X上的實值連續函數族稱為次可加的,如果?n,m ∈N 和x ∈X,有fn+m(x)≤fn(x)+fm(Tnx).

?n ∈N,ε ＞0 和次可加函數族,定義

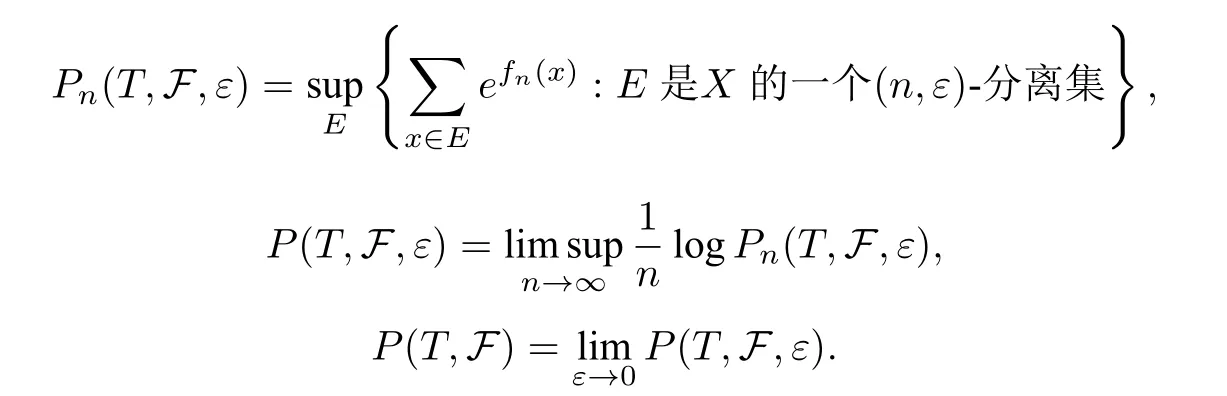
P(T,F)稱作次可加勢函數族F關于T的拓撲壓,簡記為

下面利用生成集定義次可加勢函數族關于T的拓撲壓.

?n ∈N,ε ＞0 和次可加函數族,定義

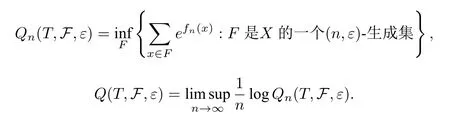
Q(T,F)=稱作次可加勢函數F關于T的拓撲壓.

記Bn(x,ε)={y ∈X:dn(x,y)＜ε}.令ηn(F,ε)=supx∈Xsup{exp(fn(y)-fn(z)) :y,z ∈Bn(x,ε)}.如果滿足Standing hypothesis,則有

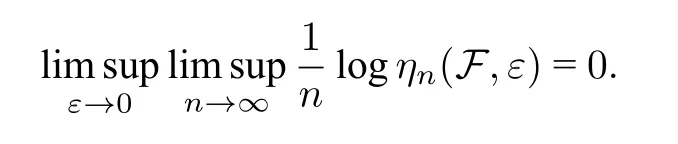
命題1 ([7])設T:X →X是緊致度量空間X上的連續映射,F是次可加勢函數族.若Standing hypothesis 成立,則有P(T,F)=Q(T,F).

定義3([8])設(X,T)和(Y,S)是兩個拓撲動力系統,T:X →X和S:Y →Y是連續映射.連續映射π:(X,T)→(Y,S)稱為因子映射，如果π是一一映射且滿足π ?T=S ?π.

1971 年,Bowen[9]利用因子映射得到

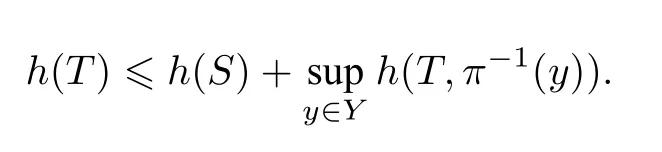
2012 年,Fang 等[8]得到關于拓撲熵及因子映射的一個重要定理:設π:(X,T)→(Y,S)是因子映射,則對于任何集合E ?X

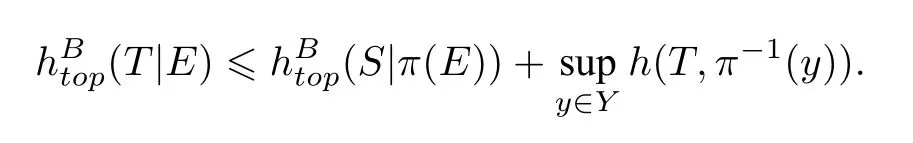
2013 年,Li 等[10]證明了:若π:(X,T)→(Y,S)是因子映射,φ:Y →R 是X上的實值連續函數,則對于任何集合E ?X,

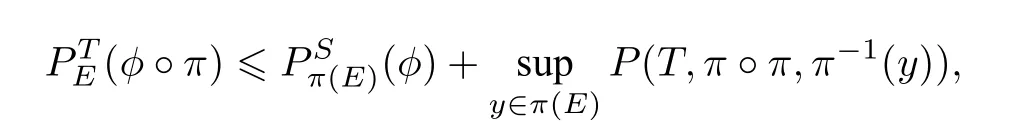
其中h(T,π-1(y))=P(T,0,π-1(y)).

2 主要定理及證明

定理1設(X,T)和(Y,S)是兩個拓撲動力系統,π:(X,T)→(Y,S)是因子映射,是Y上的次可加勢函數且滿足Standing hypothesis,則