具有變系數的時間分布階擴散方程的高效新混合有限元逼近

王芬玲，趙艷敏，史艷華，曹方方,2

(1.許昌學院 數理學院,河南 許昌 461000;2.鄭州大學 數學與統計學院,河南 鄭州 450001)

近年來,對于分布階偏微分方程的研究引起了越來越多專家學者的關注，它已經被廣泛應用于復合材料的流變特性、信號控制和處理、高分子聚合物、核磁共振以及生物醫學等領域.由于該模型的精確解不易求得，因而求它的數值解是有效的方法.例如，[1]給出了空間分布階的擴散方程有限體積法；[2]提出了一類時空有限元方法去解決相關的問題；[3]針對具有光滑和非光滑初始條件的時間分布階擴散方程，建立了有限元全離散格式并進行了誤差分析；[4]給出了具有非線性源項時間分布階的反應擴散方程的數值算法；[5]針對時間多項分數和空間分布階波動方程在非結構化網格下得到最優誤差估計.但以上的研究成果僅限于分布階偏微分方程收斂性分析方面的討論.

討論一類含變系數的二維時間分布階擴散方程高效混合有限元逼近問題.首先，借助Gauss積分對分布階算子進行近似，將原問題轉化為一個多項時間分數階偏微分方程.進而，空間方向原始變量和中間變量利用雙線性元Q11(K)和Q01(K)×Q10(K)元逼近，時間方向用修正的L1公式構造了全離散格式.然后利用數學歸納法證明了在H1模意義下該格式的穩定性，基于雙線性元和Q01(K)×Q10(K)元的高精度結果和分數階估計技巧導出了超逼近結果.最后，利用插值后處理技巧得到了相關變量的超收斂性質.

考慮一類具有變系數的二維時間分布階擴散方程為

(1)

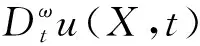
1 有限元構造和變分形式

Qij=span{xrys,0≤r≤i,0≤s≤j}.

插值算子Ih,Πh和投影算子Rh的定義為

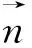
(2)

(3)

引理1[6].假設u∈H3(Ω)，則有(?(u-Ihu),?vh)=O(h2)|u|3|vh|1,?vh∈Vh.

2 逼近格式

由Gauss積分，則時間分布階導數的逼近格式為

對時間區間[0,T]進行劃分，步長τ=T/N,且tn=nτ,(n=0,1,…,N)，u(X,t)是[0,T]上的光滑函數，引入下面幾個記號為

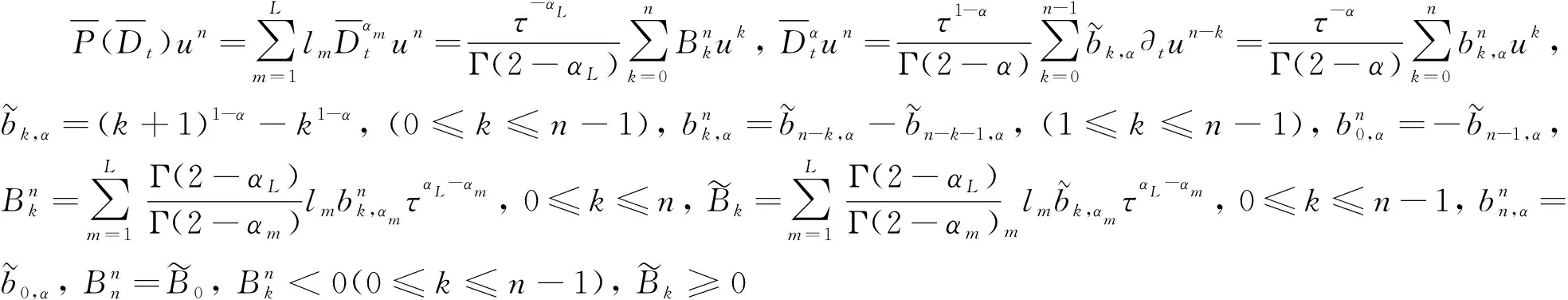
(4)

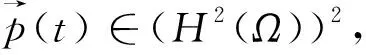
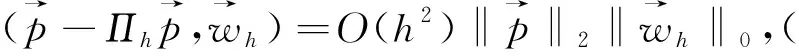
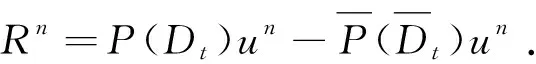
3 穩定性分析

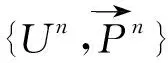
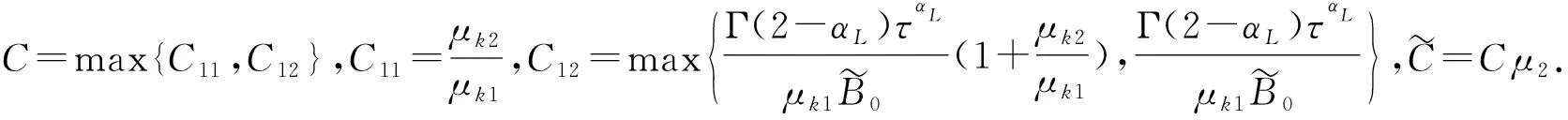
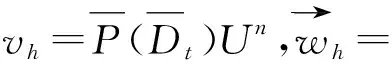
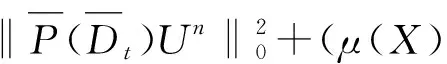
(5)

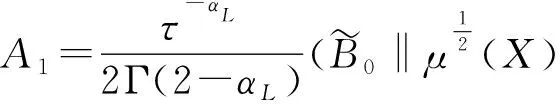
(6)

(7)

將式(6)和(7)代入式(5)中，且運用Cauchy-Schwartz不等式，則式(5)可表示為

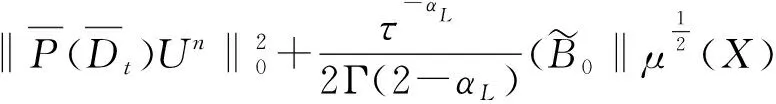
(8)

由式(8)，且利用Cauchy-Schwartz不等式和Young’s不等式，可得

(9)

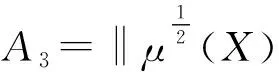
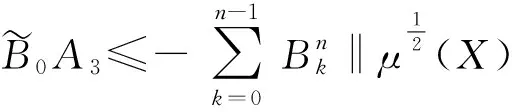
(10)

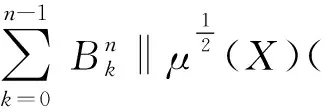
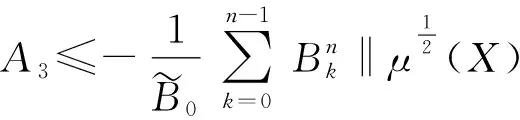
(11)

利用數學歸納法來證明下面的不等式

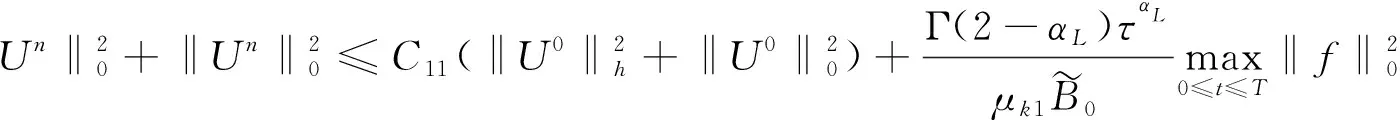
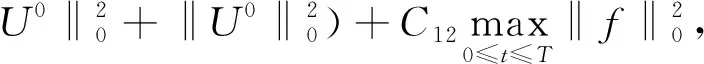
(12)

(13)

則式(12)成立.

(14)

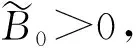
從而式(14)可變形為

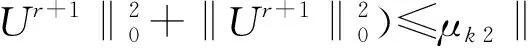
(15)

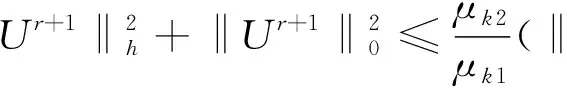
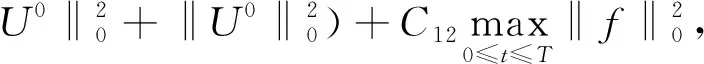
(16)

即式(12)在n=r+1也成立，在此利用模的等價性定理1的第一個結論得證.

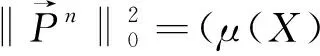
(17)

4 超逼近和超收斂分析

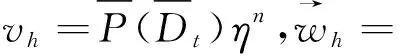
(18)

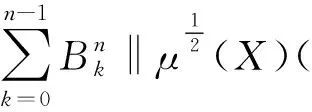
(19)

(20)

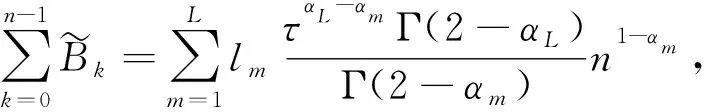
(21)

(22)

由引理4可得

(23)

由式(18)-(23)，則有

(24)

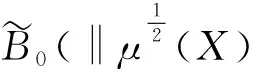
(25)

利用數學歸納法證明下面的不等式成立.

(26)

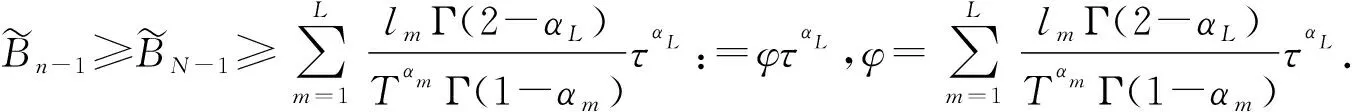
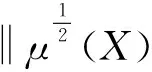
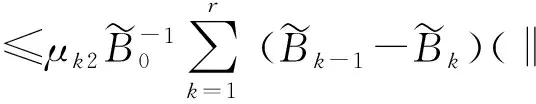
(27)

‖ηn‖1=‖Rhun-Un‖1≤C4(h2+τ2-αL+L-L-1).

(28)

根據引理2和式(28)得

‖Ihun-Un‖1≤‖Ihun-Rhun‖1+‖ηn‖1≤C5(h2+τ2-αL+L-L-1).

(29)

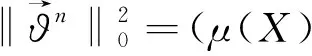
(30)

由引理2和引理3，且利用Cauchy-Schwartz不等式和Young’s不等式，可得

(31)

(32)

(33)

定理3 在定理2的條件下有如下超收斂結果

證明由引理6可知，‖un-I2hUn‖1≤‖un-I2hIhun‖1+‖I2hIhun-I2hUn‖1≤C(h2+τ2-αL+L-L-1).