以數學實驗為載體,積累數學活動經驗
——聽“鐘面上的數學”有感
?江蘇省張家港市合興初級中學 王 娟
《義務教育數學課程標準(2011年版)》指出:通過義務教育階段的數學學習,學生能參與綜合實踐活動,積累綜合運用數學知識、技能和方法等解決簡單數學問題的活動經驗.數學實驗課是一個比較好的“綜合與實踐”課題,是學生在教師的指導下,利用一定的工具(實物、軟件),通過動手操作、觀察思考、合作交流、歸納抽象等過程構建數學概念、驗證數學結論、探索數學規律、認識數學新知、解決數學問題的一種學習方式.在一次初一年級數學實驗教學研討活動中,有幸聆聽了一位數學名師執教的“鐘面上的數學”一課,很有感觸,回味無窮.
1 “回眸一想”,幫助學生積累數學思考的活動經驗
在“綜合與實踐”活動中,數學思考主要指學生通過觀察、歸納、概括、論證、計算等數學活動,學會獨立思考和清晰地表達自己的想法,發展合情推理能力和演繹推理能力,體會數學的基本思想和特有的思維方式.在具體的教學過程中,教師要積極引導學生通過回顧舊知,明晰已有知識,經歷數學思考,為后續的學習活動做好鋪墊.
教學片斷一:回眸一想
問題1一天24小時(0:00~24:00),時針、分針、秒針分別轉過多少圈?
問題2當分針轉過一圈時,時針轉過多少度?
問題3當秒針轉過一圈時,分針轉過多少度?
數學實驗:如圖1,出示掛鐘,并轉動指針.

圖1
師:請同學們觀察時針、分針、秒針的運動狀態,尋找其中的數學知識.通過小組協同學習,歸納、總結時針、分針、秒針同一時間內轉過的角度及它們數量間的關系.(3分鐘后)
生1:我代表第1小組發言.我們認為,時針每分鐘轉過的角度是0.5°,分針每分鐘轉過的角度是6°,秒針每分鐘轉過的角度是360°.
師:你們還有其他發現嗎?
生2:我代表第3小組發言.我們發現鐘面被分成了12個大格、60個小格,如果把格點和鐘面的中心連起來,那么,每個小格對應的角度是6°,每個大格對應的角度是30°.
師:很好!你們歸納的這些隱藏在鐘面的生活常識,正是重要的數學知識,是我們解決許多實際問題、數學問題的依據、基礎.
教學思考:利用三個基本問題,學生充分回顧、整理了已有的知識,厘清了時針、分針、秒針轉動過程中,鐘面上隱含的數學知識以及它們之間的關系,并能利用這些知識解決一些簡單的問題.這種實物觀察、歸納驗證,正是數學發現與驗證結論的常用方法,通過這樣的活動,幫助學生積累了數學思考的活動經驗,充分體現了執教者豐富的教學經驗、深厚的教學功底.
2 “靜心一算”,幫助學生積累主動學習的活動經驗
學生是學習的主體,“綜合與實踐”的一個教學目標是,通過有趣的問題,促進學生積極主動、生動活潑地學習與思考.教師要放手讓學生去操作、嘗試、討論、總結、提煉,在活動中有感悟,有體驗,有發現,獲得收益.本節課,教師以學生的認知發展水平和已有的知識經驗為基礎,通過問題串引領學生采用多樣化的主動學習方式,取得了很好的學習效果.
教學片斷二:靜心一算
問題4從0點的位置起,經過多少分鐘,時鐘的時針和分針第一次互相垂直?
數學實驗:教師出示掛鐘,如圖2.生3上臺演示,學生進行觀察.

圖2
師:通過觀察,你發現了什么?請先獨立思考.
2分鐘后小組內交流,然后再全班展示.(3分鐘后)
生3:從鐘面上看,時鐘的時針和分針第一次互相垂直,也就是說分針轉過的角度與時針轉過的角度的差應該是90°.
師:如何將這個問題轉化為一個數學問題呢?
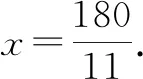
師:很好,通過引人變量x,利用方程很快解決了這個問題.
教學思考:應用方程將“時針和分針第一次互相垂直”轉化為“6x-0.5x=90”,就是學生經歷將實際問題抽象為數學問題的過程.事實上,學生在生活中已經積累了一些數學原始的、初步的經驗,通過觀察、討論、交流,讓生活經驗與數學知識“有效對接”,使得生活經驗“數學化”,這是我們平時教學中需要關注的學科素養.因此,在數學探究活動中,教師應給學生充足的時間和空間,讓學生參與看書學習、實物觀察、獨立思考、小組學習、全班展示等學習活動,在活動中積累主動學習的活動經驗.
3 “動手一做”,幫助學生積累探究活動的活動經驗
問題探究指的是從數學的角度發現和提出數學問題,綜合運用數學知識分析和解決簡單的問題,獲得分析和解決問題的基本方法,增強運用意識,提高實踐能力.積累探究經驗不是通過簡單的活動和思考就可以完成的,需要結合真實的情境,讓學生經歷感知數學、深度思考與解決問題的完整過程,能夠在學習與體驗、想象與推理、概括與運用中感悟數學方法,發展數學思維,增進數學想象,實現數學創造.同時,在動手“做數學”的過程中,激發學生的學習興趣,調動學習的熱情,建立學習的自信,啟思明理,積累經驗,提升素養.
教學片斷三:動手一做
問題5時針與分針從第一次互相垂直到第二次互相垂直時,時針與分針轉過的角度之間有什么關系?
數學實驗:教師出示掛鐘,調轉鐘面上的指針,使時針與分針重合在12點處,再次調轉鐘面上的指針.學生從圖3到圖4觀察時針與分針轉過的角度之間的關系,再分組討論.教師巡視.(3分鐘后)

圖3
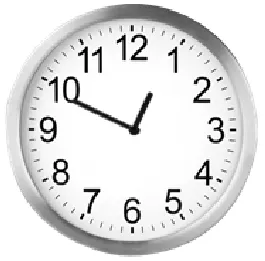
圖4
生5:我們可以將圖3與圖4中垂直時的分針與時針看成一個直角,并且把它們放在同一個圖形中(在黑板上畫出圖5).設第一次垂直的位置是OA⊥OB,第二次垂直的位置是OC⊥OD,再延長BO.
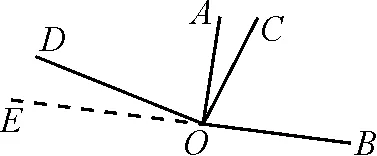
圖5
師:很好!請你們觀察圖5,先獨立思考,看看有什么結果?(2分鐘后)
生6:因為∠COA+∠AOD=90°,∠EOD+∠AOD=90°,所以∠EOD=∠AOC.
師:很好.這一結果告訴我們什么呢?
眾生:時針與分針從第一次互相垂直到第二次互相垂直時,時針比分針少轉了180°.
師:根據這個事實,你們能設計什么問題,如何用數學知識來解決呢?請先小組內討論,把問題與結論記錄下來,5分鐘后再展示.(5分鐘后)
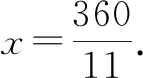
生8:(問題6)從0點開始,到12點結束,時針與分針互相垂直的次數是多少?
師:這是一個很好的問題!如何解決呢?說說你的思路.
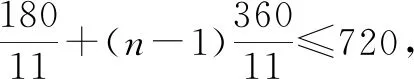
師:生8給我們提供了一個解決問題6的方案,但是,我們還沒有學習不等式的相關知識,生8無法求得最后的結果.大家討論一下,能否給出一個解決問題辦法?(2分鐘后)
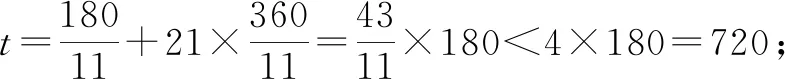
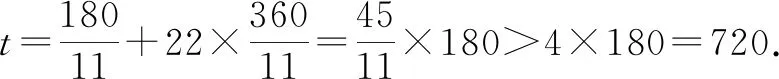
所以,n的最大值為22.也就是說從0點開始,到12點結束,時針與分針互相垂直的次數是22次.(全班掌聲一片!)
…………
教學思考:從問題5的提出到問題6的提出和解決,學生經歷了操作實驗、幾何推理、數學計算、數學驗證的全過程,獲得了數學活動經驗和數學思考經驗,提高了數學抽象、邏輯推理、直觀想象、數學運算等關鍵能力.同時,通過這一環節,學生學會了研究問題、解決問題的途徑,積累了探究活動的活動經驗.
4 “明白一理”,讓學生數學活動經驗的積累走向深入
我們知道,數學經驗在持續積累的過程中,需要學生之間、師生之間的交流、總結以及自我反思.在交流與反思的過程中,讓學生充分體會實際操作經驗、數學活動經驗、探究活動經驗,促進學生認知思維的縱深拓展,讓學生的數學探究活動走向深入.
教學片斷四:明白一理
師:從問題1到問題6,我們都是從實際問題出發,將其轉化為數學問題,最后解決問題,其過程如圖6所示.

圖6
教學思考:在數學教學中,我們的教學目標不能僅限于一節課,應把目光放得更長遠一些,立足于為學生的終身發展服務.因此,在課堂小結時,一方面要加強對數學知識、思想方法、技能技巧的歸納、整理;另一方面要重視對數學知識獲取的途徑、思維活動的過程、探究活動的經歷進行回顧、反思,使學生對數學知識的理解從量的積累到質的飛躍,同時還能獲得最具有數學本質、最具價值的數學活動經驗,讓數學課堂教學真正從有效走向高效.
數學活動經驗是看不見、摸不著的,也難以言表,而積累數學活動經驗的過程是一個不斷上升、不斷內化的過程,需要師生共同的努力.因此,教師要適時地給學生提供有效的探究性學習的時間與空間,學生要在親歷中體驗,在體驗中積累,在積累中不斷成長.只有這樣,我們的數學教學才是有品味的,有意義的,才能有詩和遠方.

