變換法在全等三角形解題中的運用
西華師范大學數學與信息學院 李佳潔 湯 強
1 引言
全等三角形的證明作為幾何研究領域重要的一個分支[1],對學生邏輯思維和抽象轉換能力有較高的要求.隨著新課程改革,中考中出現的有關全等三角形證明的考題難度也在逐步提高,對題干信息的提取不僅僅局限于直接觀察可得出,很多時候需要對圖形進行變換,方可得到所需要的證明條件.因此,如何變換圖形,轉變已知條件為新的條件,成為學生在證明兩個三角形全等的難點.本研究將以“變換法在全等三角形解題中的運用”為主題,針對初中生解全等三角形過程中可能會運用到的變換法進行系統整理歸納,并提出這些變換法對不同題型的應對策略,更好地幫助學生證明三角形全等[2].
2 變換法之一:軸對稱變換
軸對稱變換即將一個圖形沿一條直線翻折得到它的關于軸對稱的圖形.通過軸對稱變換得到的圖形與原圖形全等,并且二者的對應點連線與對稱軸垂直平分,對應點到對稱軸上任一點的距離相等[3].
例1如圖1,在等腰直角三角形ABC中,AC⊥BC,AC=BC,線段BD為∠CBA的角平分線,問:線段BC,CD與AB有什么關系?
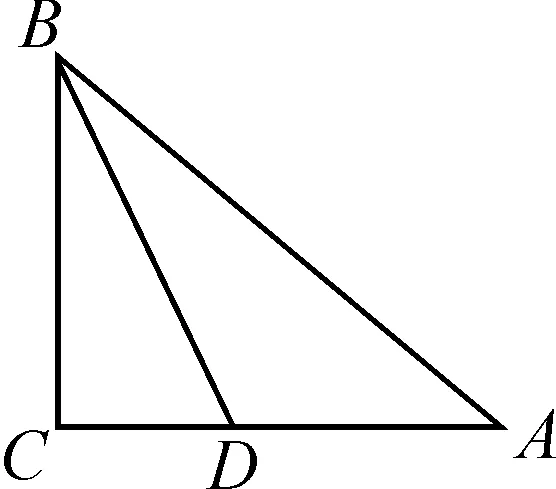
圖1
分析:該問題中,由已知條件“線段BD平分∠CBA”引導學生想到軸對稱變換,以BD為軸翻折△BCD使得C點與BA邊上的點E重合,連接DE,從而由軸對稱變換可得BC=BE,DE=CD,△BED≌△BCD,∠BED=90°;已知△ABC是等腰直角三角形,由其性質可得∠A=45°,DE=AE,等價代換有AE=CD,因此得到結論:BC+CD=AB.我們發現該題還可以運用截長補短來證明,但顯然用截長補短的方法沒有軸對稱變換構造出的條件多,因此選擇軸對稱變換法極大地提高了解題效率.
結論:AB=BC+CD.
證明:如圖2,已知線段BD平分∠CBA,將CB沿角平分線翻折后,令C落在線段AB上的對應點為E,由翻折可知△BED≌△BCD.

圖2
∴CB=EB,∠CBD=∠EBD,
CD=DE,∠C=∠BED=90°.
∵△ABC是等腰直角三角形,AC⊥BC,
∴∠A=45°.
∴△ADE是等腰直角三角形,
∴AE=DE=CD.
又AB=BE+AE=BC+CD,
∴AB=BC+CD.
因此,線段BC,CD之和等于AB的長度.
3 變換法之二:中心對稱變換
平面內使任意一對對應點A,A′的連線段都通過一個點O,且被這一點所平分,則該變換叫做中心對稱變換(也稱作反射或點對稱).關于中心對稱的兩個圖形全等,二者的對應點連線都經過對稱中心且被對稱中心平分,并且對應線段平行且相等.
例2△ABC中,AC=5,AB=7,求△ABC的中線AO的取值范圍.
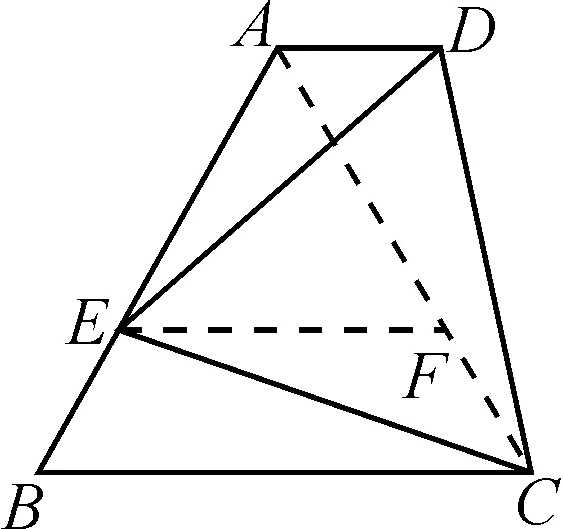
分析:凡是題干中出現“中線”“某線段2倍”這樣的字眼,除了會想到用截長補短法,我們還可以運用圖形的中心對稱變換,如圖3,將△ACO以點O為中心作中心對稱變換,得到△EBO,則有△EBO≌△ACO,BE=AC.由三角形的性質定理可知,在△ABE中,AB-BE 圖3 解:將△ACO以點O為中心作中心對稱變換得到△EBO,則△ACO≌△EBO. 于是AC=BE,AO=OE. 又在△ABE中,AB-BE 所以AB-AC<2AO 即2<2AO<12. 因此,1 旋轉變換作為一種重要的解題方法,通過將圖形繞一定點旋轉得到一個與之全等的圖形.借用旋轉變換的全等性,極大程度簡化了解題步驟. 例3如圖4,在ABCD中,A,E,D三點共線且AB=AE,過點E作直線EF,在直線EF上取一點G,使得∠BGE=∠BAE,連接GA,BG.FE與DC相交時,∠BAE=90°,求線段EG,AG,BG之間的數量關系. 圖4 證明:如圖5,將△AGE繞A點順時針旋轉90°,得△ABQ. 圖5 ∴△AEG≌△ABQ, ∴∠GAQ=90°, AQ=AG, EG=QB,∠AEG=∠ABQ. ∵∠BGE=∠BAE=90°, ∴∠AEG+∠ABG=180°. ∴∠ABQ+∠ABG=180°. ∴Q,B,G三點共線. 又∵QG=QB+BG=EG+BG, 平移變換通過對平面圖形按一定方向進行平移,得到新的圖形,二者之間的對應邊存在平行關系,對應點的連線也都平行.平移變換在初中幾何解題中更多是對于平移變換思想的運用,如下題. 例4如圖6,在四邊形ABCD中,AD∥BC,點E是AB上一個動點,若∠B=60°,AB=BC,且∠DEC=60°,判斷AD+AE與BC的關系,并證明你的結論. 圖6 分析:通過連接AC,將梯形的問題轉化為等邊三角形問題.利用平移變換作平行線,根據已知條件和平行的相關性質定理,以及結合等邊三角形的性質,通過證明三角形全等解決問題. 結論:BC=AD+AE. 證明:連接AC,過點E作EF∥BC,交AC于點F. ∵AB=BC,∠B=60°,EF∥BC, ∴△ABC與△AEF均為等邊三角形. ∴∠AEF=∠AFE=∠EAF=60°,∠EFC=120°,AE=AF=EF. 圖7 又∵∠DEC=60°, ∴∠AED=∠FEC. 又∵AD∥BC, ∴∠EAD=120°. ∴∠EAD=∠EFC. 又∵AE=EF, ∠AED=∠FEC, ∴△ADE≌△FCE. ∴AD=FC. ∴BC=AD+AE. 綜上,我們可以發現,在全等三角形的解題過程中變換法相比截長補短、倍長中線等方法具有極大的優勢,其中最明顯的就是可以直接得出變換后的圖形與原圖形全等,從而簡化解題步驟,使學生的數學邏輯思維更加清晰化.此外,在面對圖形錯綜復雜、條件繁多的情況時,通過變換法可以使題中隱蔽的條件關系明朗起來,更容易找到解題途徑.因此,巧用變換法證明三角形全等對學生而言是十分重要的.
4 變換法之三:旋轉變換





5 變換法之四:平移變換

6 結論

