例析規避勾股定理及其逆定理混用的策略
甘肅省平涼市崇信縣第二中學 位雅楠
1 引言
在初中數學課本中,有很多與“勾股定理”和“勾股定理逆定理”類似的定理,它們是互逆定理,條件和結論正好相反,學生在運用時極易出現混用錯誤.如何規避這種錯誤,是提高學生幾何定理解決問題的關鍵.
2 例析規避策略
例1如圖1所示,∠ADB=90°,AD=3,BD=4,AC=12,BC=13.求陰影部分的面積.
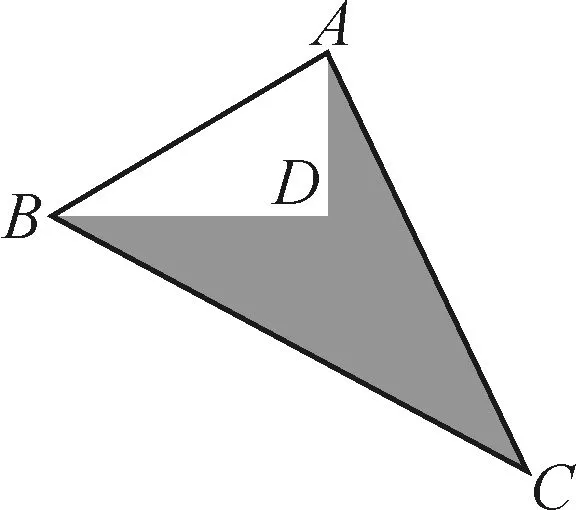
圖1
錯解:∵∠ADB=90°
∴△ABD是直角三角形,
由勾股定理,得
AD2+BD2=AB2.
∵AD=3,BD=4
∴32+42=AB2,
∵AB>0,
∴AB=5.
∴△ABD的面積為3×4÷2=6.
∵△ABC的底和高分別為AB和AC,
∴△ABC的面積為5×12÷2=30.
∴陰影部分的面積為30-6=24.
分析:在錯解當中,誤將△ABC是直角三角形當成已知條件.而本題條件中并未直接給出△ABC是直角三角形,也就不能將AB和AC看成△ABC的底、高.正確的做法應是在計算面積之前,先用勾股定理逆定理證明△ABC是直角三角形,并指明直角或斜邊,然后再計算△ABC的面積.
正解:∵∠ADB=90°
∴△ABD是直角三角形,
由勾股定理,得AD2+BD2=AB2.
∵AD=3,BD=4,
∴32+42=AB2.
∵AB>0,
∴AB=5.
∴△ABD的面積為3×4÷2=6.
∵AB=5,AC=12,BC=13,
∴52+122=132,
即AB2+AC2=BC2.
∴△ABC是直角三角形,∠BAC=90°.
∴△ABC的面積為5×12÷2=30.
∴陰影部分的面積為30-6=24.
點評:勾股定理是由直角三角形得到a2+b2=c2,這時候直角三角形是已知的,且是由“形”到“數”的過程.而勾股定理逆定理是由a2+b2=c2得到直角三角形,這時候直角三角形是未知的,是需要證明的,且是由“數”到“形”的過程[1].由此觀之,這類問題其實是“數形結合思想”的充分體現,在解決之初就應明確是知“形”求“數”,還是知“數”求“形”.
例2如圖2所示,在四邊形ABCD中,∠DBC=90°,AB=9,AD=12,BC=8,DC=17,求四邊形ABCD的面積.
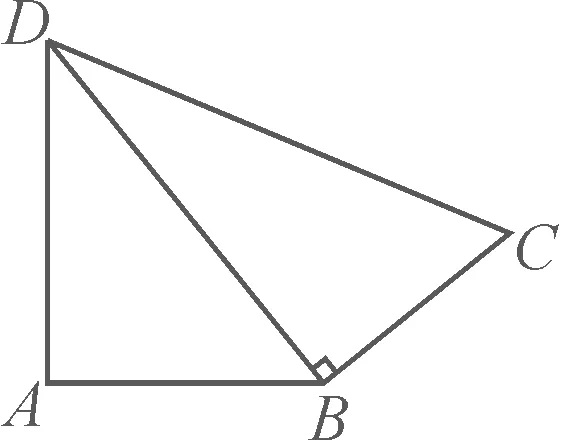
圖2
錯解:∵∠DBC=90°,
∴△BDC是直角三角形.
由勾股定理,得BD2+BC2=DC2.
∵BC=8,DC=17,
∴DB2=172-82.
∵DB>0,
∴DB=15.
∴△BDC的面積為15×8÷2=60.
∵△ABD的底和高分別為AB和AD,
∴△ABD的面積為9×12÷2=54
∴四邊形ABCD的面積為60+54=114.
分析:和例題1一樣,本題的解題過程也出現了沒有先判斷△ABD的形狀就貿然看成直角三角形求面積的錯誤.所以,本題的糾錯關鍵在于先利用勾股定理逆定理證明△ABD是直角三角形.
正解:∵∠DBC=90°,
∴△BDC是直角三角形.
由勾股定理,得BD2+BC2=DC2.
∵BC=8,DC=17,
∴DB2=172-82.
∵DB>0,
∴DB=15.
∴△BDC的面積為15×8÷2=60.
∵AB=9,AD=12,BD=15,
∴92+122=152,
即AB2+AD2=BD2.
∴△ABD是直角三角形,∠DAB=90°.
∴△ABD的面積為9×12÷2=54.
∴四邊形ABCD的面積為60+54=114.
點評:求一個圖形的面積,如果該圖形是由多個直角三角形組成,那么需先證明這些圖形為直角三角形,而不能將直觀感受的結果作為證明結果,這樣就犯了“我以為”的錯誤.“我以為”這種錯誤,是很多初中生容易犯的錯誤,主要表現在“未證先用”上.本題錯解就犯了這樣的錯誤.
例3如圖3所示,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,點E是AD的中點,求CE的長.
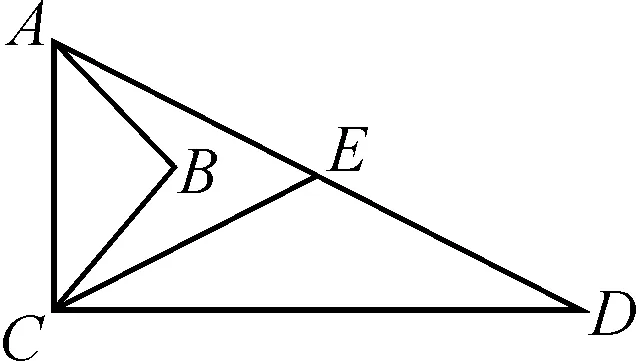
圖3
錯解:∵△ABC是直角三角形,AB=3,BC=4,
∴由勾股定理,可得AC=5.
∵△ACD是直角三角形,點E是AD的中點.
分析:本題求CE的長主要應用到了直角三角形斜邊中線定理,但該定理的使用前提是已知三角形為直角三角形.而本題錯解中,并未事先證明該三角形是直角三角形,便貿然將△ACD看成直角三角形進行計算,顯然不符合數學嚴密的邏輯性特點.
正解:∵△ABC是直角三角形,AB=3,BC=4,
∴由勾股定理,得AC2=AB2+BC2,
即AC2=32+42.
∵AC>0,
∴AC=5.
∵52+122=132,
∴△ACD是直角三角形,∠ACD=90°.
∵點E是AD的中點,

∵AD=13,
點評:直角三角形在幾何題中出現的幾率非常大,而學生不能根據主觀感覺貿然判斷三角形的形狀,應根據題目所給條件先證明其正確性才能為后面解題所用.
3 結語
要想有效規避“勾股定理”和“勾股定理逆定理”的混用,就要回歸到“勾股定理”和“勾股定理逆定理”的本質,即是知“形”求“數”,還是知“數”求“形”[2].如果是知“形”求“數”,那么說明已知三角形為直角三角形,此時應該使用勾股定理;如果是知“數”求“形”,那么說明三角形的形狀還未知,此時應該使用勾股定理逆定理進行判斷.

