拖錐系統管路延遲時間分析研究

姜延歡，吳婭輝，楊軍，劉淵，謝興娟，田森

（航空工業北京長城計量測試技術研究所計量與校準技術重點實驗室，北京 100095）

0 引言

準確可靠的靜壓是飛機計算空速、高度的重要參數，常用的靜壓測量方法主要有GPS參考高度法、真空膜盒氣壓計法、拖錐法等。然而，除拖錐以外的幾種試飛方法大多存在校準精度難以滿足國際適航認證等缺點。拖錐系統主要通過安裝在飛機內部的收放機構將拖錐放到飛機尾部后1～2倍展翼位置處，通過靜壓管上的靜壓孔將空氣引入管內進行測量，能夠避免機身附近復雜流場的影響［1］，實現靜壓的準確測量，進而確保飛行高度和飛行速度的準確測量［2］，因而廣泛地適用于各種飛行測試。不足之處在于拖錐導管與壓力傳感器之間的距離較長，引起拖錐系統的時間延遲嚴重。因此，對拖錐系統的延遲時間進行深入分析，確定其影響在測量系統精度容許范圍內，是保證拖錐測量數據有效性的必要條件［3-4］。

拖錐系統的概念模型最早由道格拉斯飛機公司于1959年提出［5］，對于飛行中的飛機而言，拖錐系統管路的長度超出一定翼展后，靜壓場將不受飛機周圍的流場干擾［6］，可以測得穩定的靜壓。隨后，道格拉斯飛機公司、皇家航空機構、海軍測試中心、聯邦航空局和美國國家航空咨詢委員會均對拖錐系統進行了設計及測試。美國國家航空咨詢委員會在針對空速的測量精度和測量程序的研究中指出，粘性延遲隨飛機飛行高度、垂直下降速度和拖錐軟管長度增加而增大，但與軟管直徑成反比［7］。

目前，針對拖錐系統管路壓力時間延遲的理論研究主要有兩種方法：一種是基于壓力管路的動態特性研究系統的遲滯特性，從而確定系統的遲滯指標；另一種是基于小擾動理論推導出管路的靜壓延遲時間。

中國商飛上海飛機設計研究院的宋歌［8］基于所建立的管路模型，并結合流體力學中的哈根-泊肅葉（Hagen-Poiseuille）流動公式，得到靜壓延遲時間的理論模型，為了便于分析，其假設空速系統中的所有管路均為直管路，并將帶有管路的空速系統等效為一階系統，推導出管路的靜壓延遲時間。

航空工業成飛的李南伯［9］針對民機適航試飛靜壓測試中的靜壓校準計算機誤差分析進行了研究，考慮到聲學延遲的影響比重較小，故僅考慮了黏性延遲的影響，給出了拖錐系統管路中由黏性延遲引起的壓差計算方法。

航空工業洪都650所的湯黃華［10］基于JL8飛機的靜壓系統開展研究，將靜壓系統簡化為包含進氣管和泄氣管的容器，對靜壓系統施加階躍壓力信號，獲得系統壓力的響應規律，從而確定系統進氣和泄氣過程中的遲滯指標。

寧波大學的朱國瑞［11］在針對航空器壓力測量管路的遲滯特性進行理論研究時，基于小擾動假設，將管路內的流動簡化為一維層流的準定常流動，同時忽略運動方程中的慣性力項及管內氣流的徑向運動，在流動為等溫過程、管路入口為等速率變化時，得到粘性壓力滯后，但是該公式只能在層流條件下才能夠很好地預測管路的滯后特性，且適用于管長與管徑比l/D=102～103的范圍。

綜上所述，在對管路的延遲時間開展理論研究時，考慮到模型本身的復雜性及計算的成本，將管路系統簡化為一階系統，并基于連續方程和動量方程對管路系統從時域建模是常用的方法。雖然簡化后的模型仍能夠對工程設計進行理論指導，但是往往都有其特殊的應用范圍，這主要還是因為模型過度簡化導致模型的預測能力降低。對于拖錐系統而言，飛機的飛行工況復雜，加之拖錐系統自身包含超長的管路，使得管路內的流動也隨之變得復雜，將管路系統簡化為一階系統無法真實反映其管路延遲時間。基于時域的建模方法則需要重點考慮管路摩擦力造成的粘性延遲對壓力響應遲滯的影響，進而實現拖錐系統延遲時間的準確預測。為此，本文基于連續性方程和動量守恒方程對拖錐系統管路系統進行建模，并在此基礎上研究管路結構參數和環境參數對拖錐系統管路時間延遲的影響規律。

1 拖錐系統管路建模

管路中可壓牛頓流體流動過程的建模主要考慮連續性方程和動量守恒方程。連續性方程假設流體為連續介質模型，流體宏觀物理量是空間點及時間的連續函數。對拖錐系統壓力延遲的模擬主要是研究系統內的流動和壓力分布狀況，并作出如下假設：①拖錐系統管路中的氣體介質滿足連續性介質假設；②管路內的氣體滿足理想氣體狀態方程；③拖錐系統的管路為絕熱，管路內部氣體介質與外界環境之間不存在熱傳遞［12］；④管路內部氣體流動徑向的空間梯度忽略不計，即流動被認為是一維的［13］；⑤流體性質在橫截面上取平均值，并且僅取決于軸向位置和時間［14］；⑥管路中氣體的流動方向垂直于重力加速度方向，因此，忽略重力的影響。

連續性方程為

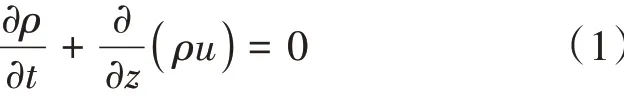
式中：ρ為拖錐系統中可壓縮氣體介質的密度，kg/m3；u為氣流速度，m/s；t為時間，s；z為管道沿軸線的位置，m。

為了能夠更準確地描述拖錐系統氣體壓力延遲過程，必須考慮管路璧產生的摩擦力，包含摩擦力的動量守恒方程為

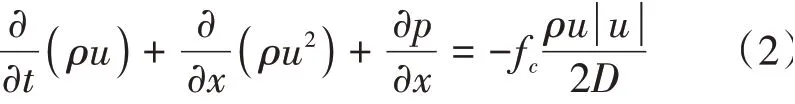
式中：fc為可壓縮摩擦因子；D為管路直徑；p為氣體介質的壓力。管路中的氣體滿足理想氣體狀態方程，即p=ρRgT。其中Rg為空氣的氣體常數，J/（kg·K）；T為介質的溫度，K。管路內的壓降Δp可通過Darcy-Weisbach公式計算，即

不可壓縮流的Darcy摩擦因子f和可壓縮摩擦因子之間存在如下關系

式中：γ為比熱比；Ma為馬赫數，Ma=u a，其中聲速a的計算方式為

Darcy摩擦因子f是計算管路中摩擦力的主要參數，當管路內的流動為層流時，f可通過如下公式計算［15］

式中：Re為流動的雷諾數，其計算方法為

式中：η為氣體介質的動力粘性系數，N·s/m2。

當管路中為湍流時，f可通過Haaland方程進行計算［15］

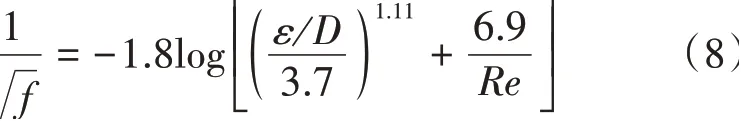
式中：ε為管路璧面的絕對粗糙度，m。

當管路中的氣體介質由層流向湍流轉變時（即Recr，min＜Re＜Recr，max），f可通過差值進行求解。當流體由層流向湍流轉變時，Re的臨界值Recr，min和Recr，max的計算為［15］

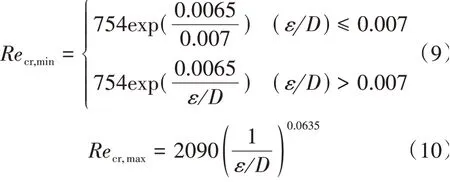
綜上所述，本文所構建的管路模型考慮了層流、層流向湍流轉變及湍流三種不同的流動狀態，適用性更強。在求解的過程中，時間項的離散格式為全隱式，密度項的離散格式為一階迎風，速度項的離散格式為中心差分與一階迎風的混合格式；時間步長定為0.000 01 s，管路的璧面粗糙度為1.5×10-5m。

2 模型驗證

為了驗證理論計算的準確性，選用激波管產生標準階躍壓力信號，試驗所采用的激波管能夠產生非常理想的階躍式壓力，階躍壓力上升時間小于等于1μs。所采用的試驗裝置如圖1所示。

圖1 階躍壓力發生裝置Fig.1 Step pressure generating device

基于階躍壓力校準裝置對計算結果進行驗證。在試驗的過程中，在激波管末端安裝標準傳感器，通過工裝在管路系統及其末端安裝被校傳感器，最后由數據采集系統完成標準傳感器和被校傳感器信號的采集。在試驗的過程中需要保持管路水平，避免管路彎曲造成的壓力損失。

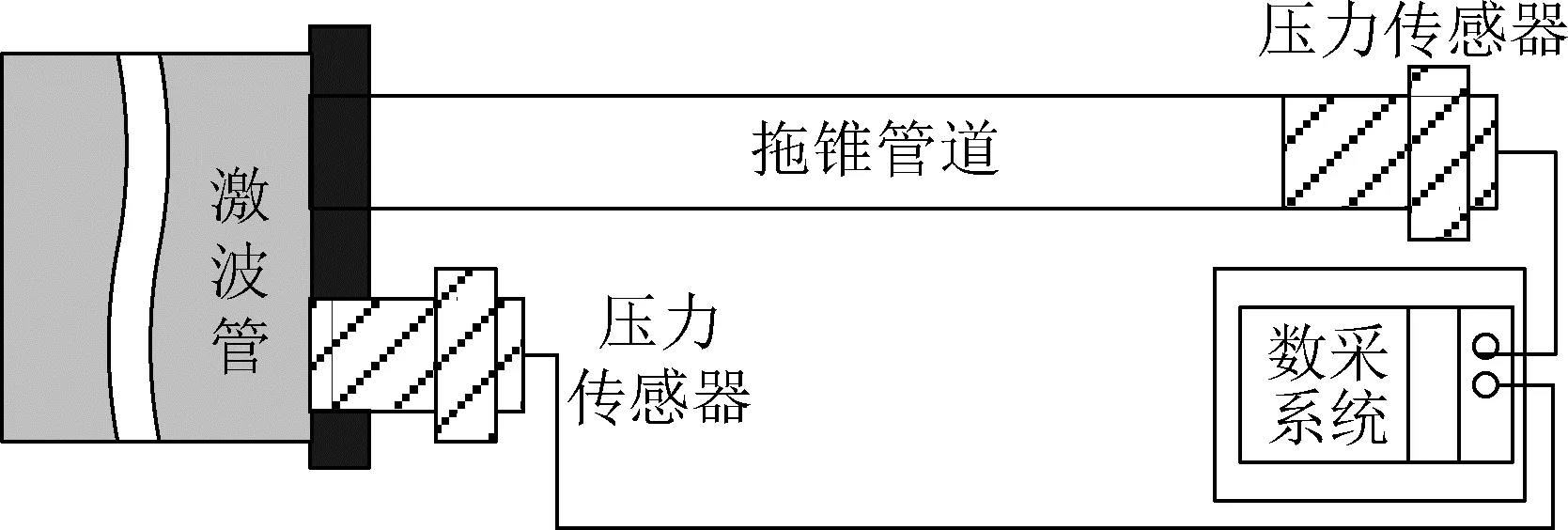
圖2 激波管末端傳感器及信號采集系統Fig.2 Sensor at the end of the shock tube and signal acquisition system

在對數據進行采樣時，采樣率設置為5 MHz。通過對比標準傳感器和被校傳感器測得的壓力信號，得到管路的延遲時間。由圖3可以看出，理論計算得到的理論延遲時間與試驗差別較小。

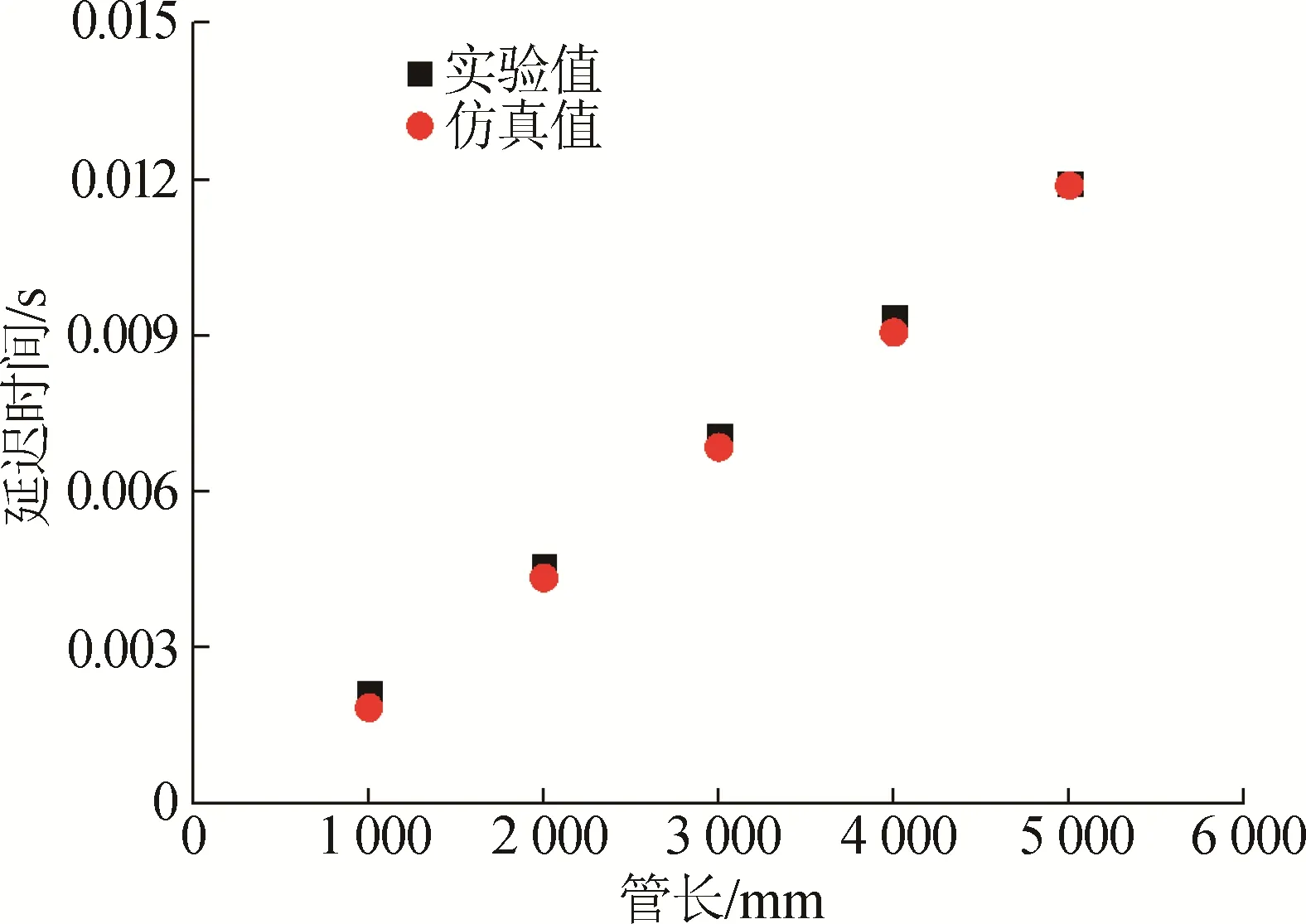
圖3 理論及試驗對比Fig.3 Comparison of theory and experiment

同時選取管長為5 m時管路末端壓力信號的幅值進行仿真，為了確保試驗信號與仿真信號的可比性，仿真過程中的激勵信號采用被校傳感器的波形。由圖4可以看出，仿真波形與試驗波形整體的符合程度較好。

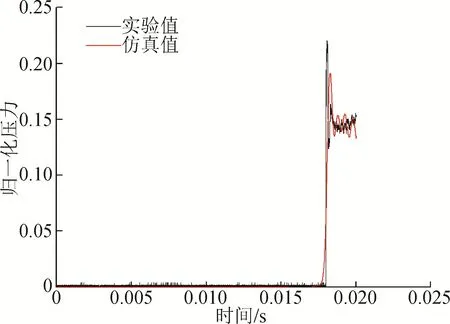
圖4 理論信號與試驗信號波形歸一化比對Fig.4 Normalized comparison of theoretical signal and experimental signal waveform

3 結果和討論

3.1 管路長度對拖錐系統延遲時間的影響研究

管長是影響拖錐系統延遲時間的核心因素，為了明確管路長度對拖錐系統延遲時間的影響規律，項目選取管長分別為5，10，20，40，60 m和80 m。對比不同管長條件下，階躍壓力信號傳遞至管路端面時的壓力分布曲線可以看出：管路長度對壓力信號的分布主要體現在壓力上升時刻、壓力峰值和壓力波形三個方面。如圖5所示，當管路直徑小于20 m時階躍信號的峰值會顯著放大，大于初始階躍信號的壓力；當管路直徑大于20 m時階躍信號的峰值顯著降低，壓力波形也呈現出明顯的雙峰形狀。

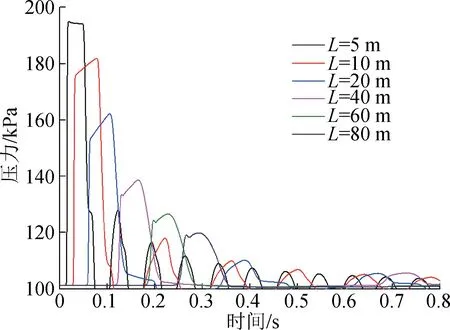
圖5 管長對拖錐管路中壓力的影響Fig.5 Effect of pipe length on the pressure in the pipe of trailing cone system

隨著拖錐系統管路長度的增大，拖錐系統管路的延遲時間呈現出線性增長的趨勢。壓力波傳播所需要的延遲時間增大，此外，管路璧對流體產生的阻力也急劇增大。在兩種延遲機理的共同作用下，拖錐系統管路的延遲時間迅速增大，如圖6所示。

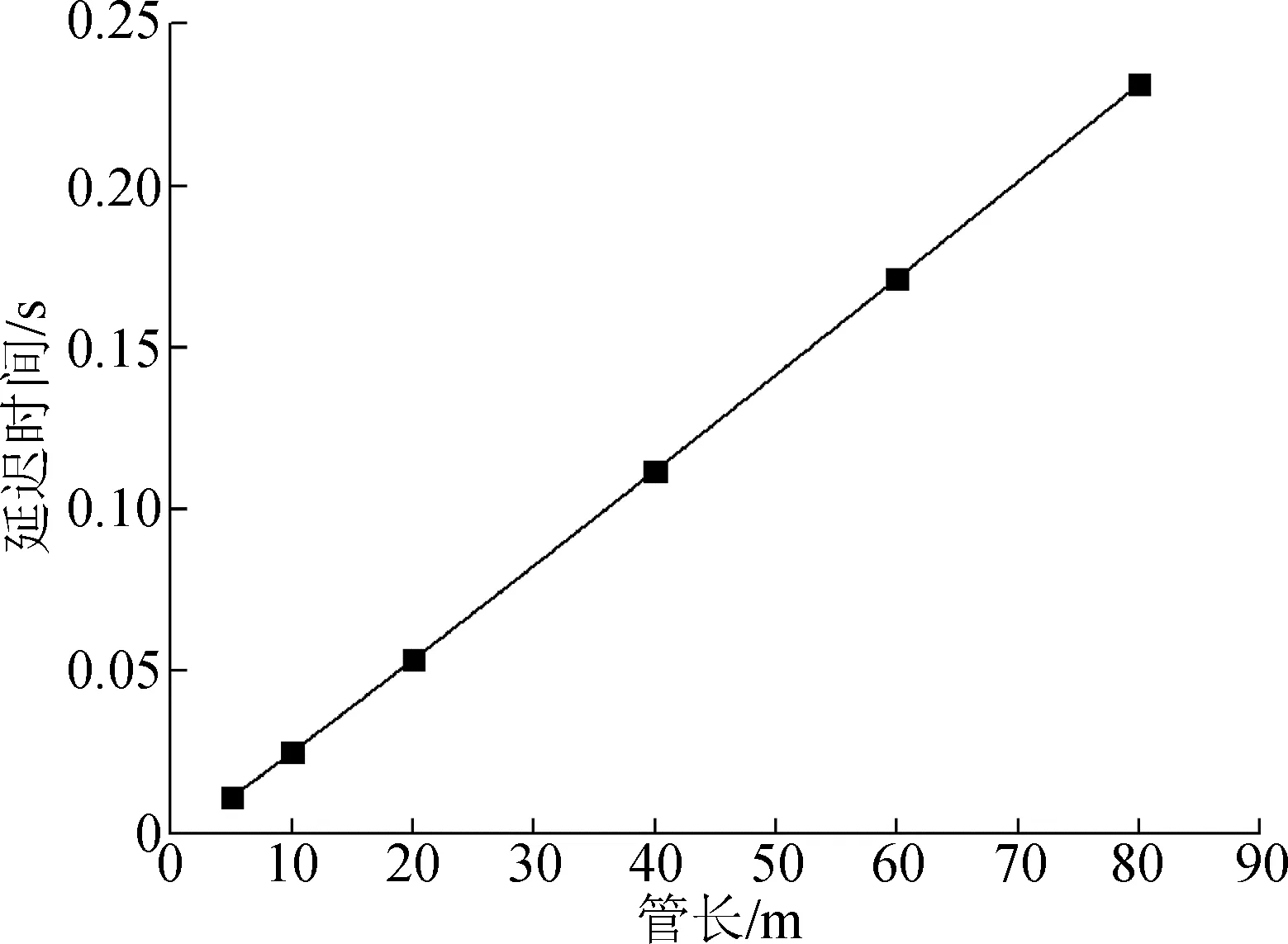
圖6 管長對拖錐管路中壓力延遲時間的影響Fig.6 Effect of pipe length on the delay time of pressure in the pipe of trailing cone system

3.2 管路直徑對拖錐系統延遲時間的影響研究

為了研究管路直徑對拖錐系統延遲時間的影響，在長度為80 m的管路入口處施加50 kPa的階躍壓力，分析管路末端的動態壓力特性，進而測得拖錐系統管路的壓力延遲時間。不同管路直徑下管路中的壓力曲線形狀相似，隨著管路直徑的增大，管路中的壓力整體增大，壓力迅速升高，所對應的時刻提前，壓力曲線第一個峰值與第二個峰值的比值不斷增大。當管徑為12 mm時，第一個壓力峰值明顯超過第二個壓力峰值，如圖7所示。

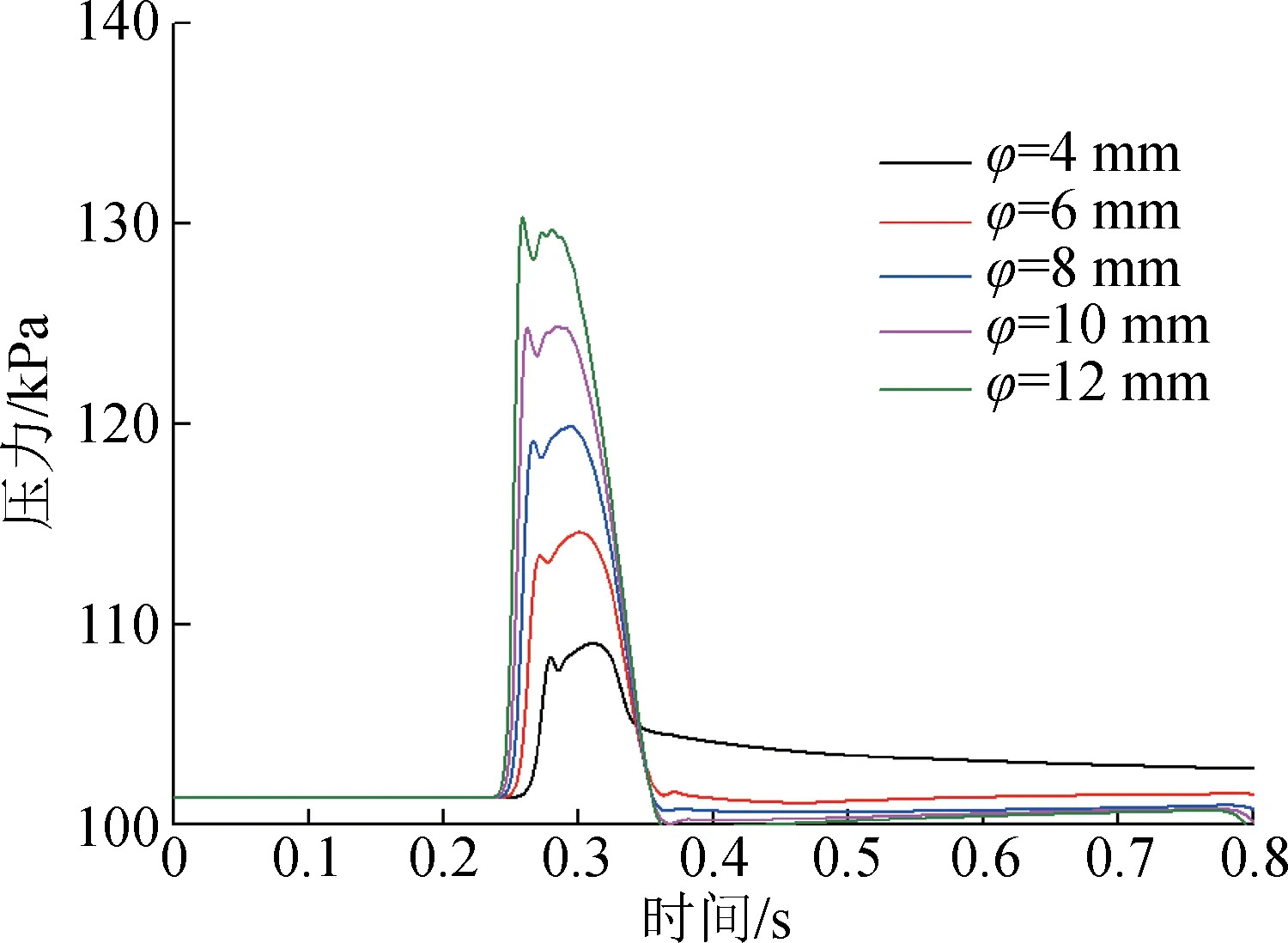
圖7 管徑對拖錐管路壓力的影響Fig.7 Effect of pipe diameter on the pressure in the pipe of trailing cone system

隨著管路直徑的增大，拖錐系統管路延遲時間呈現出非線性降低的趨勢，管路直徑為6 mm時，出現明顯的拐點，如圖8所示。這主要是由于隨著管路直徑的增大，粘性阻力造成的延遲時間的比重逐漸降低引起的。

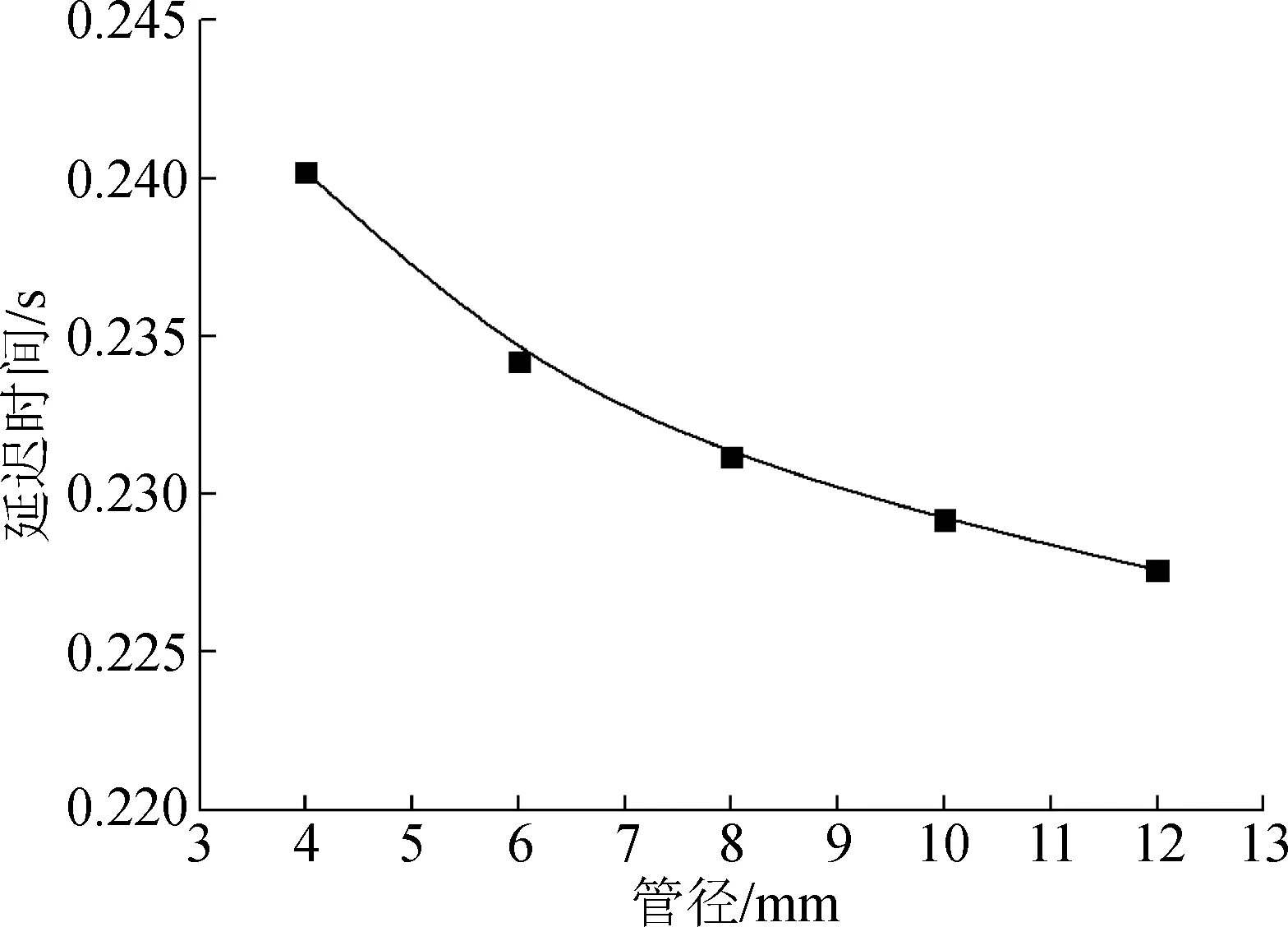
圖8 管徑對管路延遲時間的影響Fig.8 Effect of pipe diameter on the delay time of pipe

3.3 階躍壓力對拖錐系統延遲時間的影響研究

選取階躍壓力分別為10，30，50，70，90 kPa，研究階躍信號的階躍壓力對拖錐系統管路壓力分布的影響規律。可以看出，隨著階躍壓力的增大，管路末端的壓力整體增大，壓力信號的脈寬逐漸增大，壓力信號第一峰值和第二峰值的比值逐漸降低。當階躍壓力為90 kPa時，壓力信號的第一峰值顯著低于第二峰值，如圖9所示。

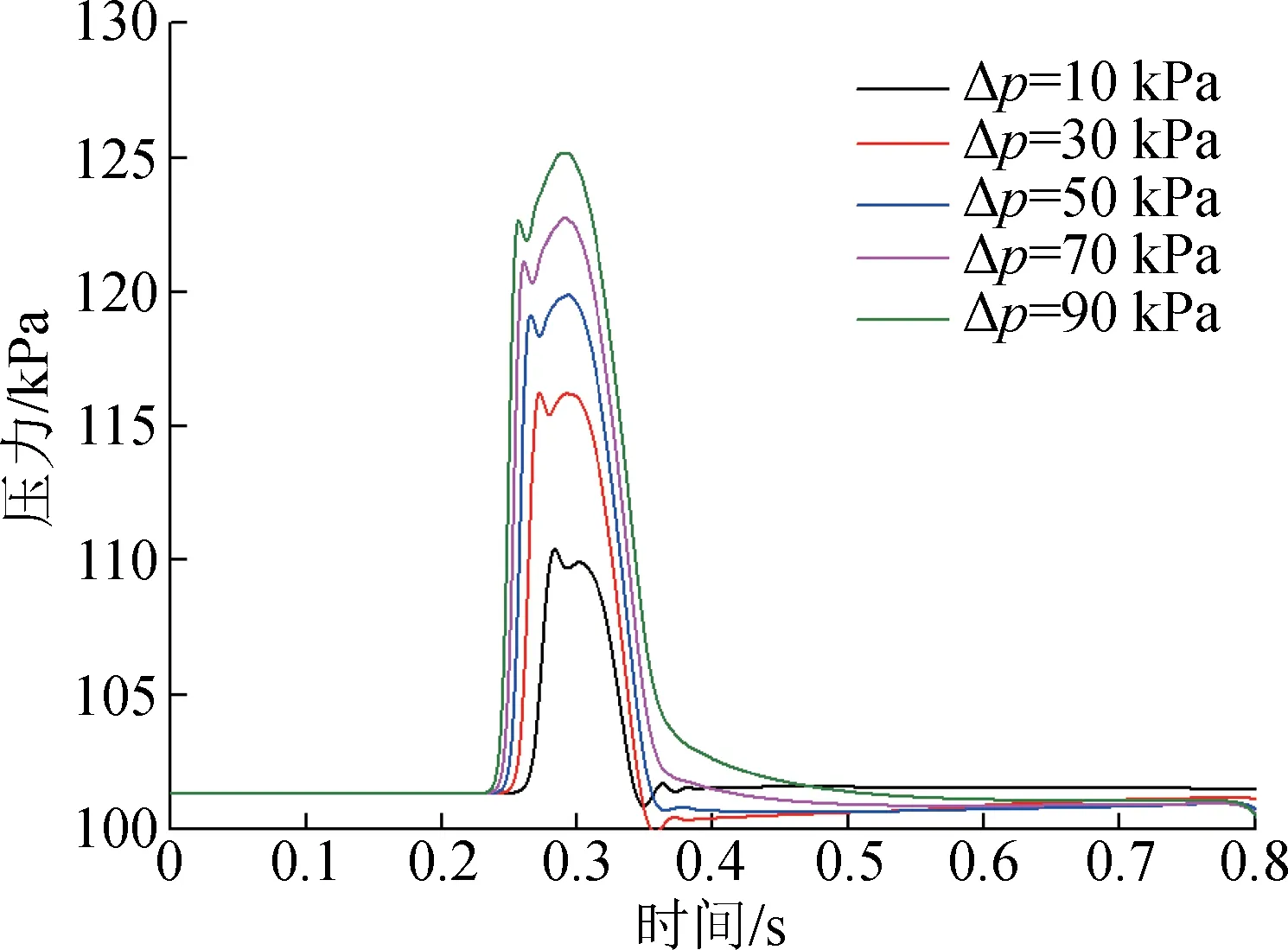
圖9 階躍壓力對拖錐管路壓力的影響Fig.9 Effect of step pressure on the pressure in the pipe of trailing cone system

由階躍壓力對拖錐管路延遲時間的影響可以看出，隨著階躍壓力的增大，延遲時間呈現出非線性降低的趨勢。這主要是由于階躍壓力的提升，增大了壓力波在管路中傳播的速度，聲學延遲時間顯著降低，然而由于速度的增大，顯著增強了管路璧對氣流的粘性阻力，由粘性引起的延遲時間增大，但延遲時間由聲學延遲時間主導，如圖10所示。

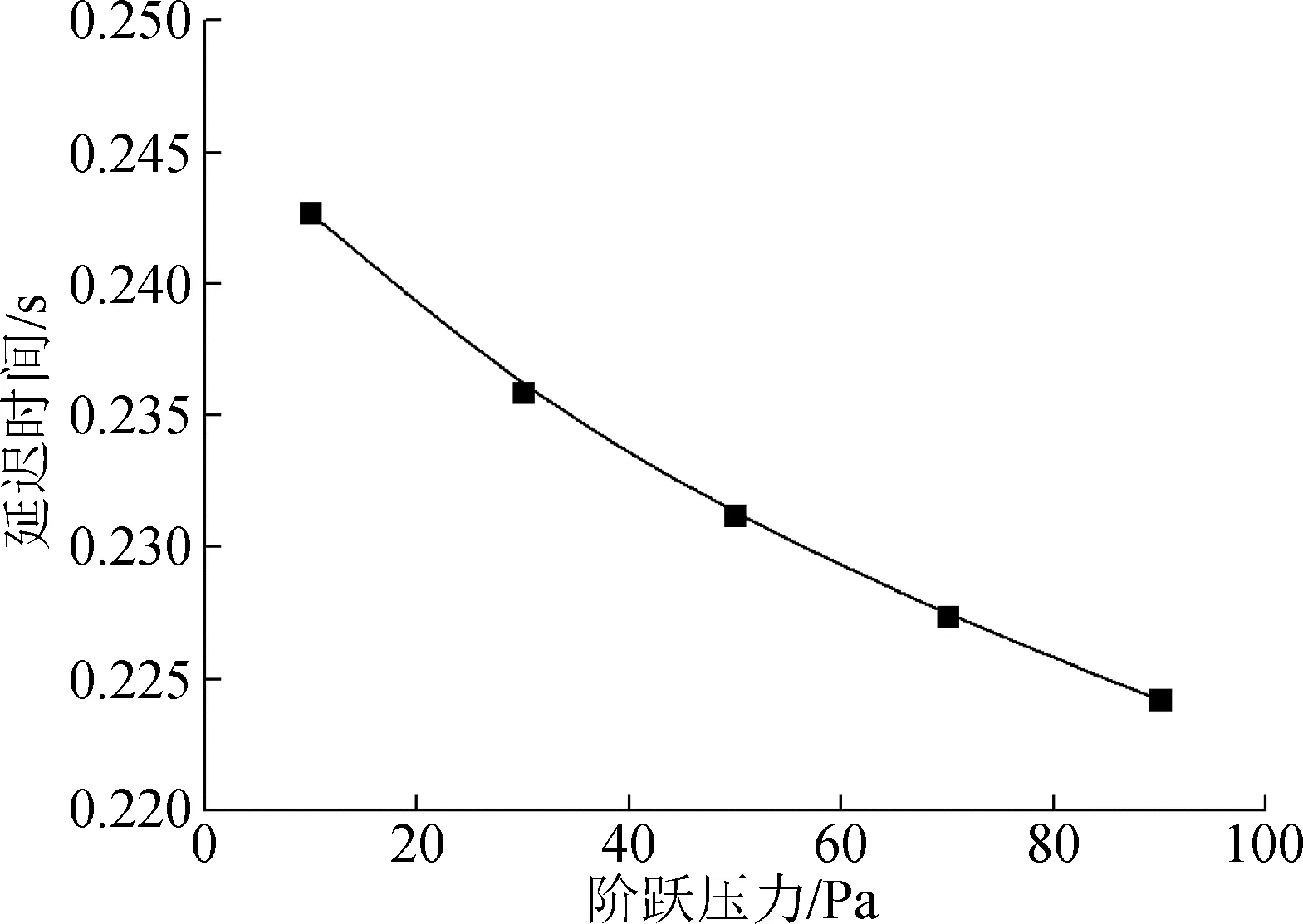
圖10 階躍壓力對管路延遲時間的影響Fig.10 Effect of step pressure on the delay time of pipe

3.4 環境背壓對拖錐系統延遲時間的影響研究

在具體的飛行過程中，飛機需要適應不同海拔的變化，其環境背壓也在不斷變化。對比不同環境背壓下管路端面的壓力分布，壓力分布的曲線形狀差別整體較小，壓力波形的脈寬、峰值差別不大，如圖11所示。

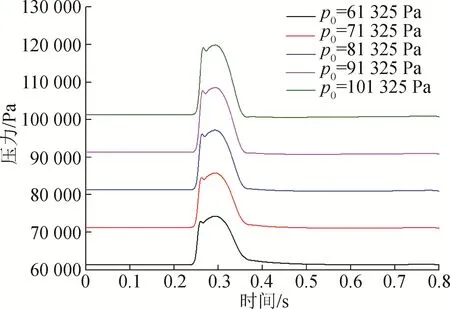
圖11 環境背壓對拖錐管路壓力的影響Fig.11 Effect of ambient pressure on the pressure in the pipe of trailing cone system

由環境背壓對管路延遲時間的影響可以看出，隨著環境背壓的增大，拖錐系統管路的延遲時間整體呈現出增大的趨勢。由于在仿真過程中階躍壓力保持一致，環境背壓的變化直接引起管路中氣體自身屬性的變化。隨著環境背壓的增大，管路中氣體的比熱比增大，導致當地聲速增大，聲學延遲降低；與此同時，密度增大，管路由于粘性產生的阻力增大。最終的綜合效果導致管路的延遲時間隨著環境背壓的增大而增大，如圖12所示。

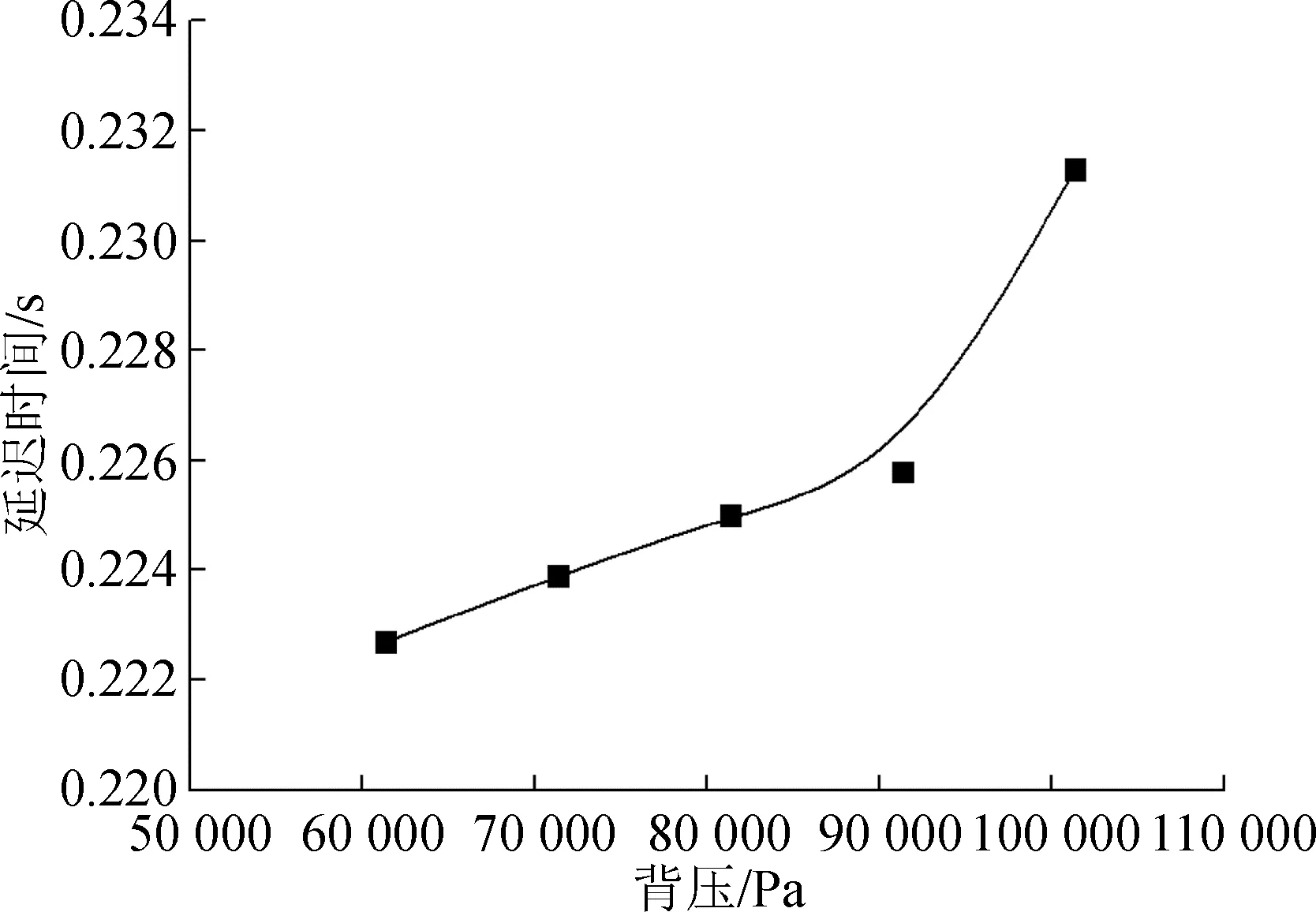
圖12 環境背壓對管路延遲時間的影響Fig.12 Effect of ambient pressure on the delay time of pipe

3.5 環境溫度對拖錐系統延遲時間的影響研究

為了模擬飛機飛行環境中環境溫度對拖錐系統管路延遲時間的影響，選取環境溫度分別為233.15，253.15，273.15，293.15 K和313.15 K。環境溫度對拖錐管路末端壓力分布曲線形狀的影響主要體現在信號脈寬、壓力曲線的第一和第二峰值上。如圖13所示，隨著環境溫度的增大，第一壓力峰值呈現出降低的趨勢，第二壓力峰值呈現出增大的趨勢，但是變化幅值均不大。

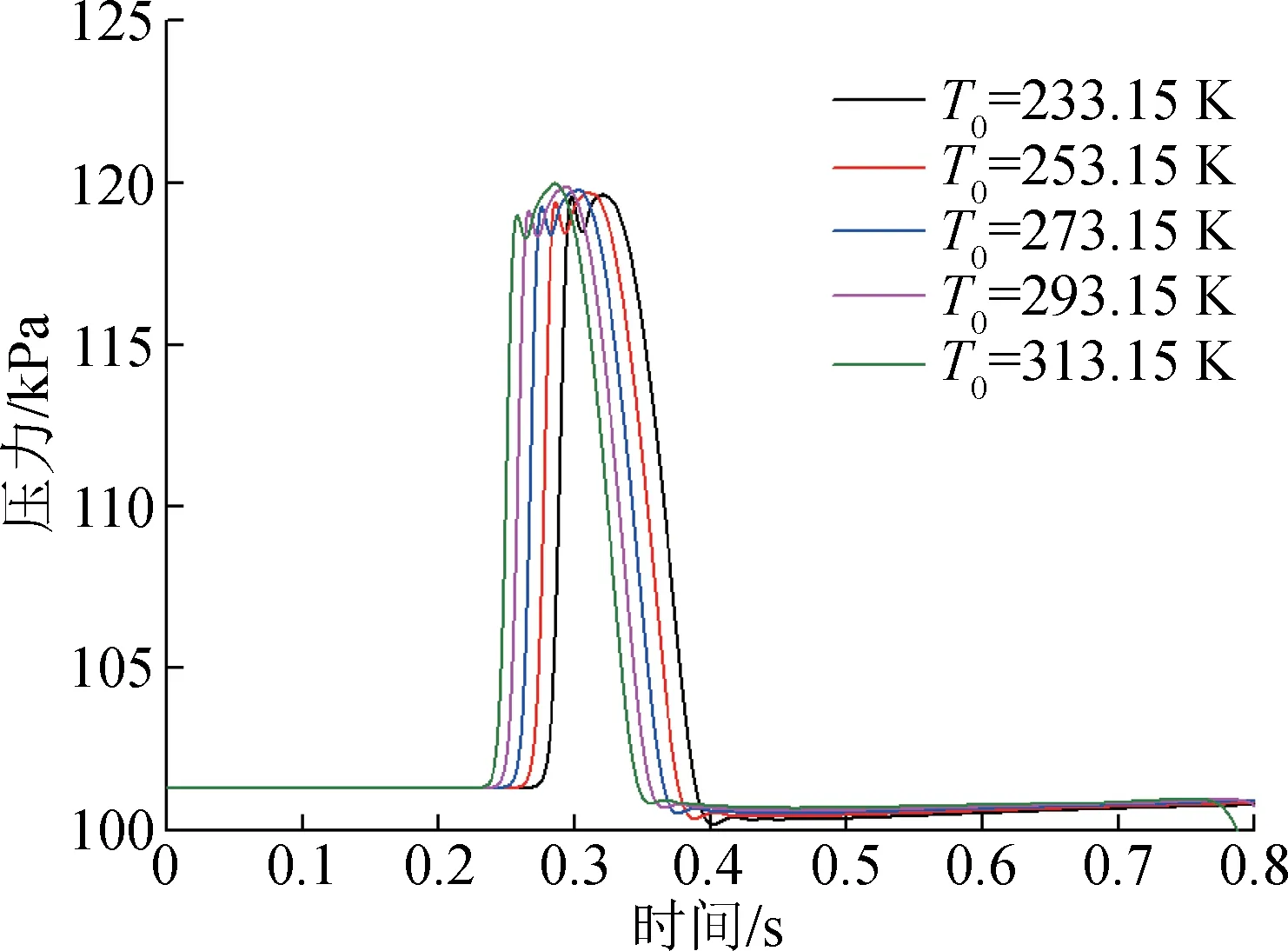
圖13 環境溫度對拖錐管路末端壓力的影響Fig.13 Effect of ambient temperature on the pressure at the end of thepipe of trailing cone system

如圖14所示，隨著環境溫度的升高，拖錐系統延遲時間呈現出非線性降低的趨勢，這主要是由于隨著環境溫度的升高，壓力波傳播的速度增大，粘性產生的阻力也降低，聲學延遲和粘性延遲均降低。

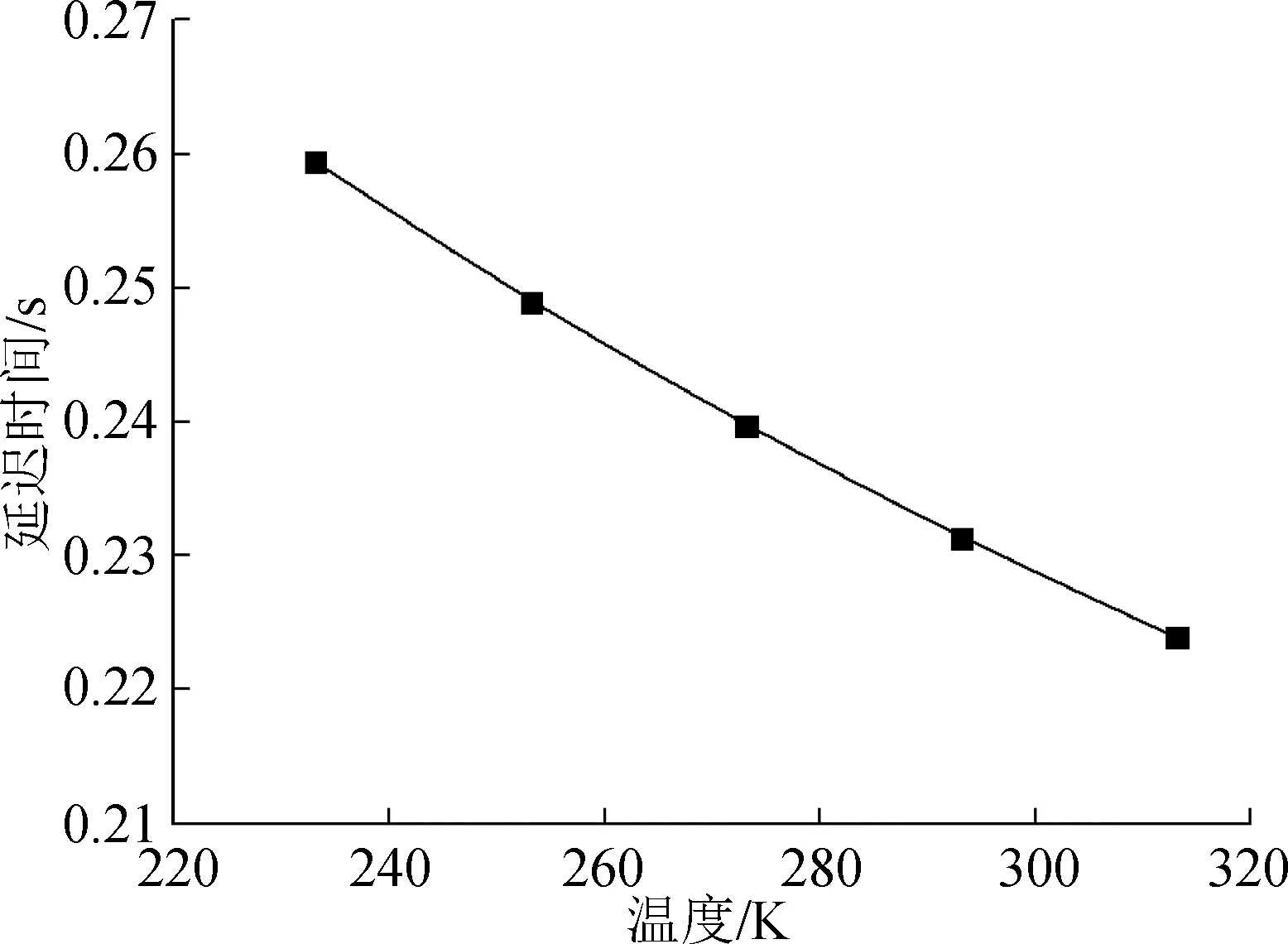
圖14 環境溫度對管路延遲時間的影響Fig.14 Effect of ambient temperature on the delay time of pipe

4 結論

拖錐系統管路壓力延遲的快速、高精度預測是確保飛行安全的基礎。本文提出了一種基于連續性方程和動量方程對拖錐管路中的可壓牛頓流體流動過程進行理論建模的方法，同時重點考慮了管路璧面粘性阻力對管路時間延遲的影響因素，更加貼近真實工況。通過與激波管試驗進行比對，驗證了所構建模型的準確性，在此基礎上，研究了管路結構參數和環境參數對管路時間延遲的影響規律，隨著拖錐系統管路長度、環境背壓的增大，管路末端階躍壓力的峰值逐漸降低，拖錐系統管路的延遲時間呈現出線性增長的趨勢。隨著管路直徑、階躍壓力的增大，管路末端的壓力增大，拖錐系統管路的延遲時間呈現出非線性下降的趨勢。隨著環境溫度的增大，拖錐系統管路的延遲時間呈現出非線性下降的趨勢。