不同海況等級下傳遞對準桿臂效應的影響研究

陳永展，袁濤，曲建嶺，魏喜坤

（1.海軍航空大學青島校區，山東青島 266041；2.阿米檢測技術有限公司，江蘇無錫 214000）

0 引言

艦載機和武器系統的定位跟蹤依靠機載慣性導航系統，通過母艦的主慣導對艦載機的子慣導進行傳遞對準。由于受到海洋環境的干擾較多，其中，對準時存在桿臂效應影響了對準精度和對準時間。

S.P.Dmitriyev等人［1］提出一種采用巴特沃斯低通濾波器對桿臂效應在線補償的方法。SEO等人［2-3］提出力學補償法的概念，并用試驗對桿臂效應誤差的力學補償法進行了驗證。李蓓［4］提出了速度誤差觀測量補償和低通濾波器兩種桿臂效應誤差的補償方法。這三種補償方法能夠對桿臂效應較好地補償，但是缺少在某一具體裝備下三種補償方法效果的對比。西北工業大學提出了艦載直升機動基座對準技術的方案設計，后來主要就系泊情況和航行情況下的艦載機初始自對準技術進行了研究，國內西北工業大學、國防科技大學、海軍航空大學等對艦載戰斗機動基座傳遞對準均取得一定理論研究成果，但在海洋環境中不同海況對傳遞對準的影響研究較少。

本文通過研究不同海況等級對傳遞對準中的等效桿臂效應，建立船舶六自由度模型，對艦載戰斗機動基座傳遞對準采用三種補償方法進行仿真分析。

1 船舶六自由度模型建立

船舶在海面上受到的干擾力不規則，力的方向和大小變化不定，很難用簡單的數學模型進行完全精準的描述。為了建立能夠描述船舶在海面上的受力情況需要進行一些前提假設，通過系統分析簡化海面的作用力，將一些影響較小的作用力進行忽略以建立六自由度模型。本文基于日本操縱性數學模型研討組的分離型思想（MMG），將船舶在海面行駛時受到的總作用力單獨考慮，分為裸船體、敞水槳、敞水舵和風浪流引起的水動力進行疊加，并且忽略海浪、海涌等外界環境對敞水槳、敞水舵的影響，用裸船體、敞水槳、敞水舵在靜水中所受的干擾力代替動水中的干擾力。

應用參考文獻［7］中簡化后的船舶六自由度模型為

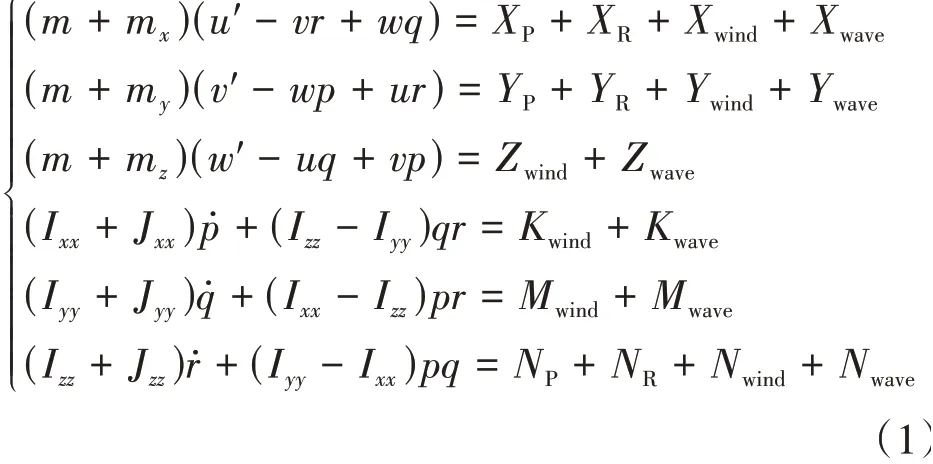
式中：m為船舶質量，kg；mx，my，mz分別為船舶沿著X，Y，Z軸的附加質量；Ixx，Iyy，Izz分別為船舶繞X，Y，Z軸的轉動慣量；Jxx，Jyy，Jzz分別為船舶繞X，Y，Z軸的附加轉動慣量；下標P，R，wind，wave分別為敞水槳、敞水舵、風、海浪對船舶的力和力矩。

1.1 附加質量

船舶平面運動附加質量估算公式為［8］

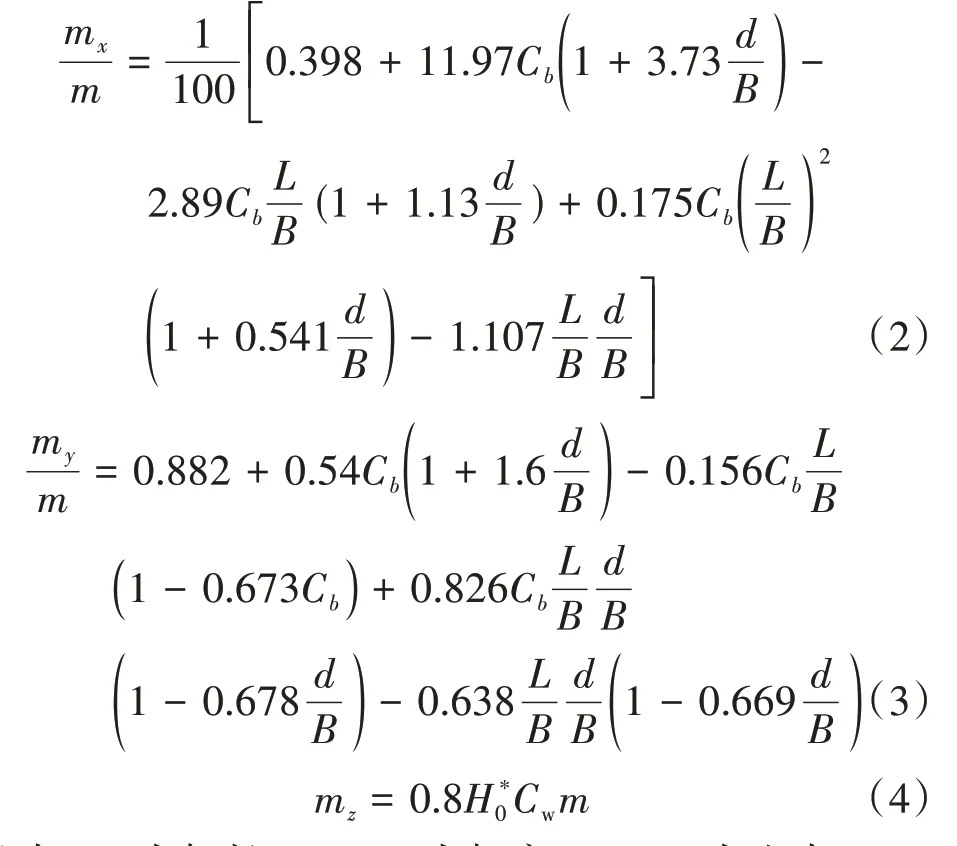
式中：L為船長，m；B為船寬，m；d為吃水，m，取標準排水量下的吃水8.96 m；Cb為方形系數；Cw為水線面系數；H*0為船中寬吃水比。

1.2 螺旋槳力和力矩計算模型

螺旋槳力和力矩表示為［9］

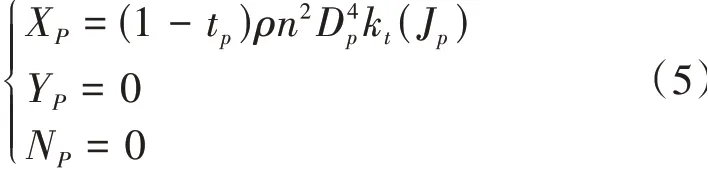
式中：ρ為流體密度，kg/m3；n為主機轉速，r/min；kt(Jp)為槳的推力系數；tp為推力減額分數；DP為槳直徑，取6.5 m。

1.3 舵力和力矩計算模型

舵力和力矩計算模型為［8］

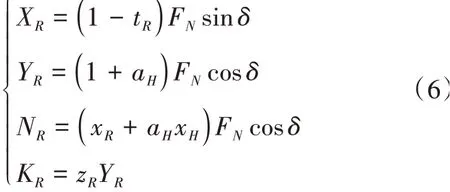
式中：FN為垂直于舵葉平面的正壓力，N；tR為舵力減額系數；δ為舵角，（o）；a H為操舵誘導船體橫向力的修正因子；x H為操舵誘導船體橫向力的作用中心到船舶重心的距離，m；xR為舵中心到船舶重心的縱向距離，m；zR為舵正壓力中心到船舶重心的垂向距離，m。

1.4 波浪力仿真數學模型

將船簡化為箱體船，得六自由度力和力矩為［10］

式中：a為波幅，m；k為波數；we為遭遇頻率；x為遭遇浪向角；ρ為流體密度，取1.025 kg/m3；g為重力加速度，取9.8 m/s2。

不同海況等級下遭遇頻率we取值見表1，為計算波浪力仿真數學模型提供數值參考。

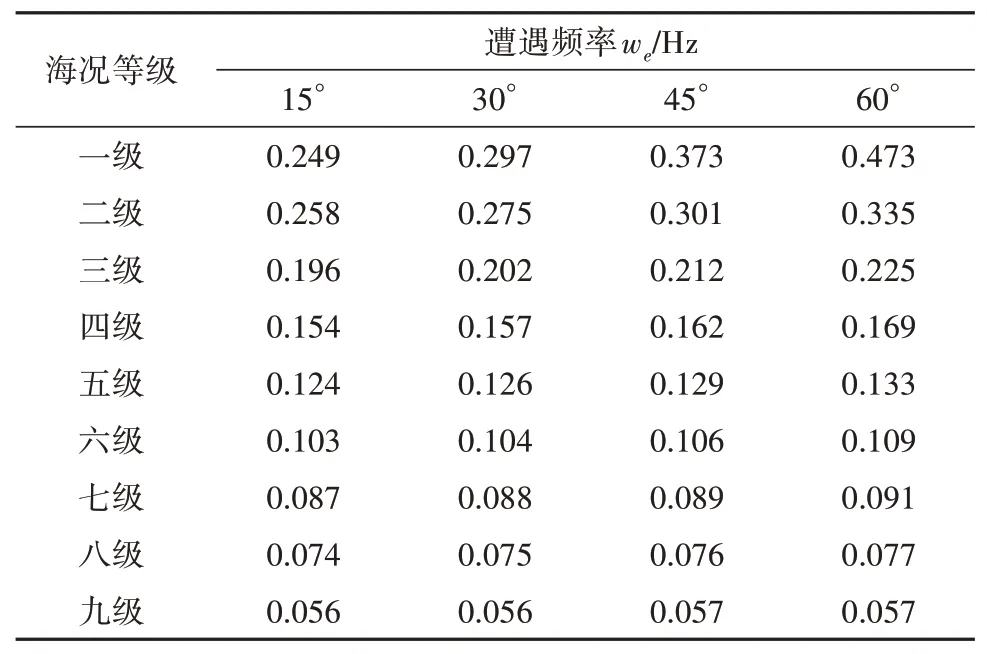
表1 遭遇頻率值（V=18節）Tab.1 Values of encounter frequency

1.5 風力和力矩計算模型

忽略風力對船舶垂蕩和縱搖的干擾，風力和力矩為［9］

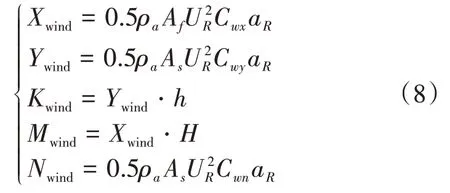
式中：Cwx，Cwy，Cwn為風壓力和力矩系數；a R為風舷角，rad；h為船舶橫向受風作用點的高度到取矩點的高度，m；H為船舶縱向受風作用點的高度到取矩點的高度，m；Af為船體水線上正投影面積，m2；As為船體水線上側投影面積，m2；ρ為空氣密度，取0.001293 g/cm3。

2 速度匹配傳遞對準卡爾曼濾波方程

2.1 卡爾曼濾波方程

卡爾曼濾波離散方程為［11］

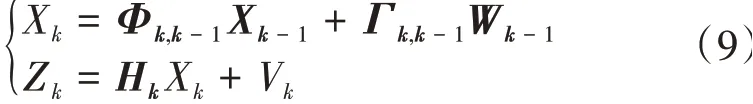
式中：Xk為系統的n維狀態變量；Zk為系統的m維觀測序列；Γk，k-1為n·p維噪聲輸入矩陣；Φk，k-1為n·n維k-1時刻到k時刻狀態轉移矩陣；Wk為p維系統激勵噪聲序列；Hk為m·n維觀測矩陣；Vk為m維量測噪聲序列。

過程噪聲和量測噪聲滿足

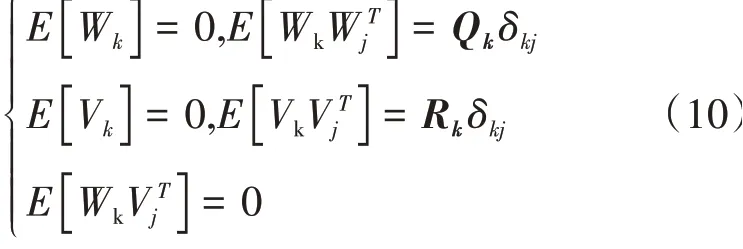
式中：Qk為系統過程噪聲Wk的p·p維對稱非負定方差矩陣；Rk為系統觀測噪聲Vk的m·m維對稱正定方差矩陣；δkj為克羅內克函數。

線性離散卡爾曼濾波狀態一步預測方程為

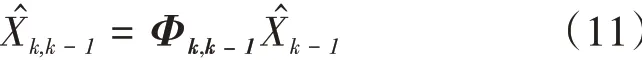
狀態估計為

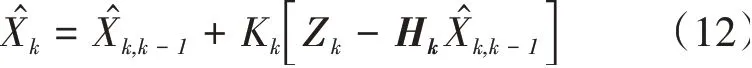
濾波增益矩陣為

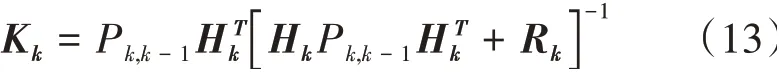
一步預測誤差方差矩陣為

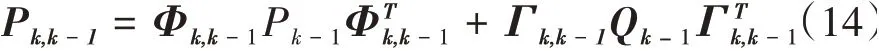
估計誤差方差矩陣為

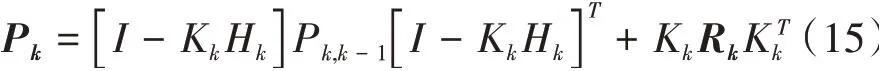
觀察分析卡爾曼濾波方程，任何系統給定初值X^0和P0，結合k時刻的觀測值Zk，就可以遞推算法計算得到k時刻的狀態估計X^k。

2.2 卡爾曼濾波狀態方程與量測方程

海洋環境仿真中，由于垂直通道影響小且垂直通道和水平通道之間的耦合小，故忽略垂直通道。

取狀態變量X為

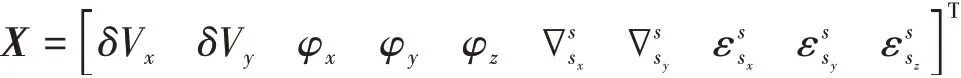
系統狀態方程為

選主子慣導間的速度差為觀測量，則觀測方程為

式中：v為滿足E(vvT)=R的零均值系統白噪聲；H為系統的量測矩陣。

卡爾曼濾波初始值為

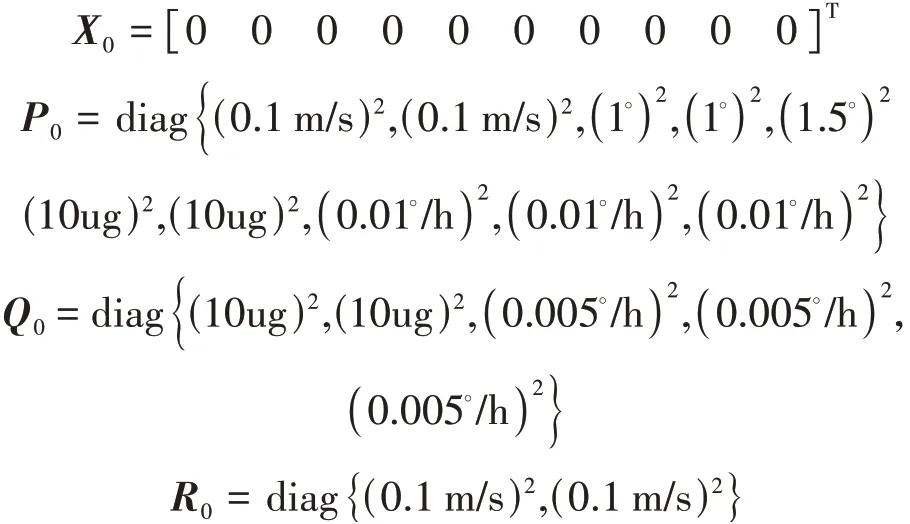
3 不同海況等級傳遞對準仿真

3.1 仿真條件

海浪搖擺產生的三軸運動屬于正弦函數，其數學模型為

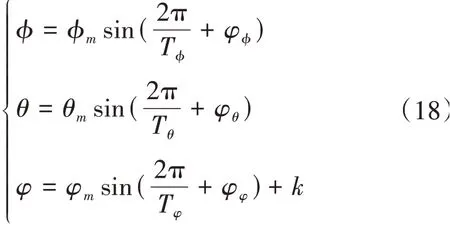
某艦六自由度模型由龍格-庫塔法解出微分方程，以不同海況進行分級，其仿真條件見表2，不同海況下橫搖、縱搖、艏搖角度幅值見表3。

表2 仿真條件Tab.2 Simulation conditions

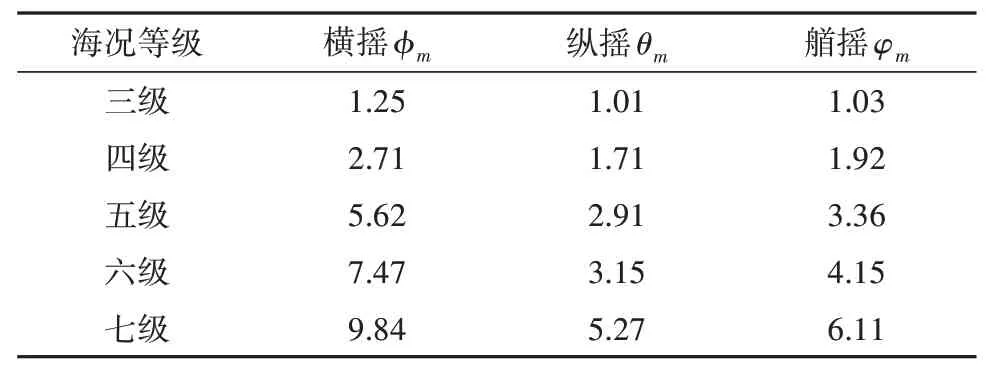
表3 不同海況等級下的橫搖縱搖艏搖角度幅值Tab.3 Amplitude of roll pitch and yaw angleat different sea state grades （°）

3.2 桿臂效應對傳遞對準的影響

考慮桿臂效應對傳遞對準的影響，設桿臂長度為(1 1 1)T，圖1為五級海況時加速度計輸出。

從圖1中可以發現加速度計輸出曲線波動幅值較大，將天向加速度數值進行提取，天向加速度數值分級統計見表4。

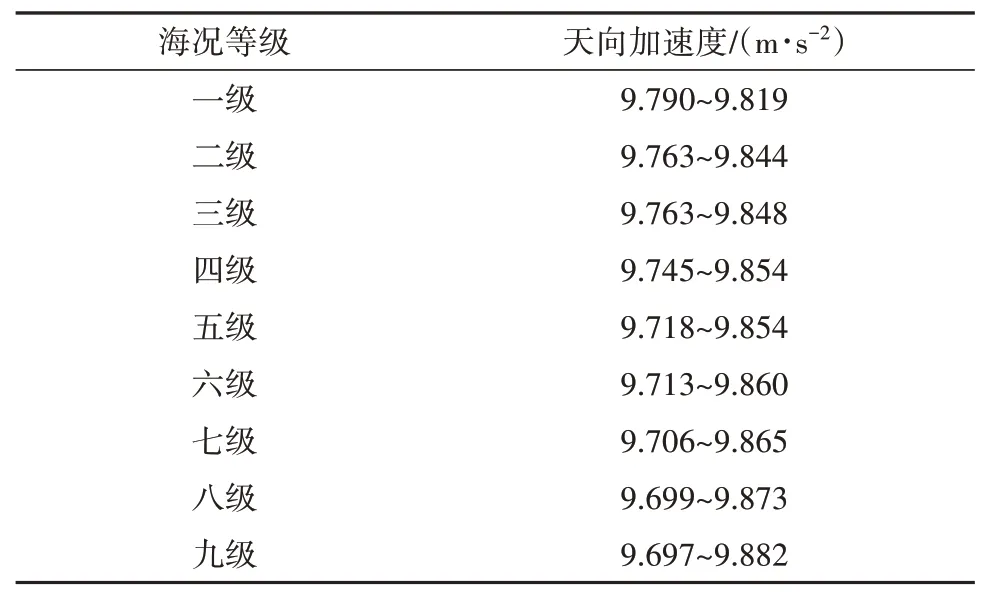
表4 不同海況等級下天向加速度范圍Tab.4 Rangesof upward acceleration at different sea state grades

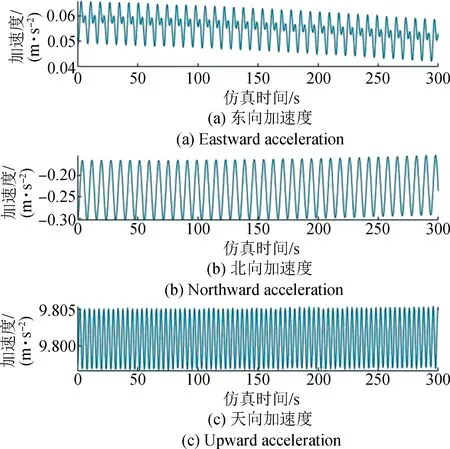
圖1 五級海況時加速度計輸出Fig.1 Accelerometer output at grade five sea state

從表4可以得出，一級海況時波動幅值為0.029，每一級海況的波動幅值都在增大，到達九級海況時波動幅值達到0.185，從一級海況到九級海況，天向加速度輸出顯著變化。

由此可見，加速度計的輸出受海況影響而不穩定，產生的等效桿臂效應對傳遞對準的影響較大，使系統整體加速度計輸出波動變化明顯，呈發散狀態不利于對準，因此在實際對準中需要對桿臂效應進行補償。

3.3 桿臂效應補償方法

3.3.1 巴特沃斯低通濾波法

卡爾曼濾波用k-1時刻的最優估計預測k時刻的狀態變量，新的最優估計是根據上一最優估計預測得到的，并加上已知外部控制量的修正，因而新的不確定性由上一不確定性預測得到，并加上外部環境的干擾，

可以考慮采取更優化的桿臂效應補償方法。

巴特沃斯濾波器的特點是通頻帶內的頻率響應曲線最大限度平坦，在阻頻帶則逐漸下降為零，且頻率特性曲線無論在通帶內還是阻帶內都是頻率的單調函數。當通帶的邊界處滿足指標要求時，通帶內留有裕量。因此可用較低階數的系統將精確度均勻的分布在整個通帶或阻帶內。

桿臂效應加速度頻譜分析如圖2所示，由頻譜分析可選取通帶截止頻率0.02 Hz，阻帶截止頻率0.5 Hz，通帶衰減不得高于3 db，阻帶衰減不得低于40 db。

圖2 桿臂效應加速度頻譜分析Fig.2 Spectral analysis of acceleration of lever armeffect

采用二階巴特沃斯低通濾波器進行濾波［10］

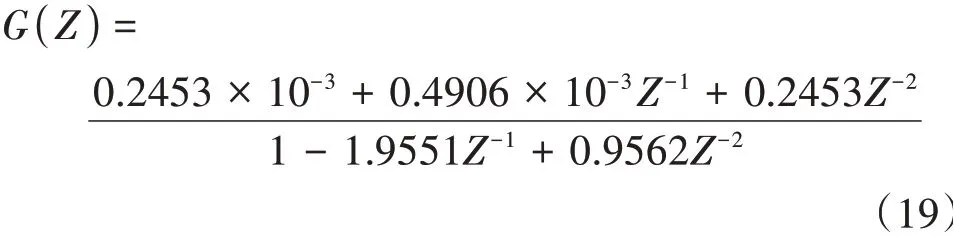
濾波器方程為

輸出方程為

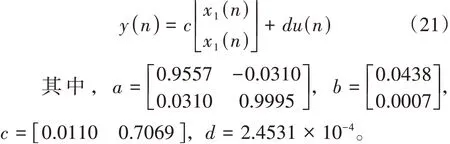
濾波后五級海況加速度計輸出如圖3所示。

圖3 巴特沃斯低通濾波前后五級海況加速度計輸出Fig.3 Accelerometer output at grade five seastate before and after Butterworth low-pass filtering

通過對比不同海況等級下的仿真圖，可以發現三軸失準角均呈現收斂狀態，濾波前后加速度計輸出范圍明顯縮小，取t=250 s時三軸失準角進行分析如圖4，仿真數據見表5。

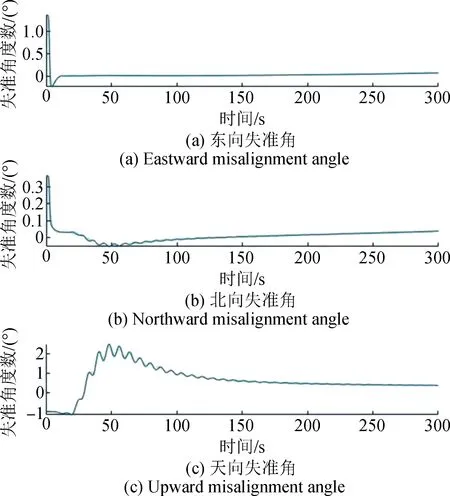
圖4 巴特沃斯低通濾波后五級海況三軸失準角變化曲線Fig.4 Changing cure of three-axis misalignment angle at grade five sea state after Butterworth low-pass filtering

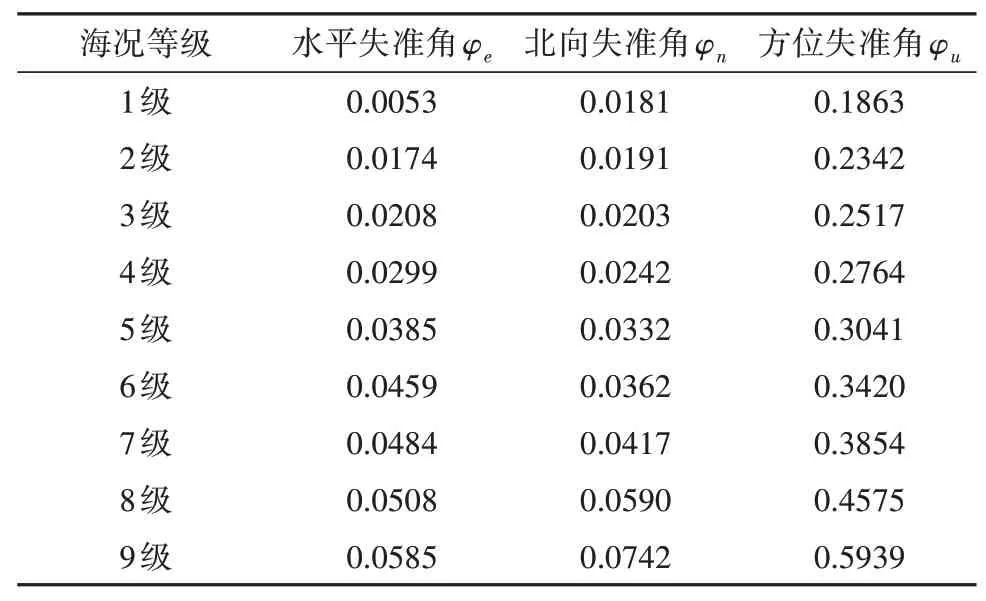
表5 不同海況等級下三軸失準角大小Tab.5 Values of triaxial misalignment angle at different sea state grades （°）

由圖3圖4和表5結合可知，四級海況時水平失準角φe在9.8 s后逐漸趨于穩定，φn在78 s后逐漸趨于穩定，穩定前波動幅值在-0.009～0.0262之間變化，幅值變化較未濾波曲線明顯減弱，方位失準角φu在0 s到150 s內振動劇烈，后在250 s處仍存在0.2764°失準角。

五級海況時水平失準角φe在11.6 s逐漸趨于穩定，φn在109 s后逐漸趨于穩定，穩定前波動幅值在-0.0169～0.0321之間變化，幅值變化較未濾波曲線明顯減弱，方位失準角φu在0 s到200 s內振動劇烈，后在250 s處仍存在0.3041°失準角。

六級海況時水平失準角φe在13 s逐漸趨于穩定，φn在122 s后逐漸趨于穩定，穩定前波動幅值在-0.027～0.03之間變化，幅值變化較未濾波曲線明顯減弱，方位失準角φu在0 s到200 s內振動劇烈，后在250 s處仍存在0.3420°失準角。

七級海況時水平失準角φe在13.8 s逐漸趨于穩定，φn在142 s后逐漸趨于穩定，穩定前波動幅值在-0.0385～0.039之間變化，幅值變化較未濾波曲線明顯減弱，方位失準角φu在0 s到220 s內振動劇烈，后在250 s處仍存在0.3854°失準角。

八級海況時水平失準角φe在15.9 s逐漸趨于穩定，φn在180 s后逐漸趨于穩定，穩定前波動幅值在-0.068～0.065之間變化，幅值變化較未濾波曲線明顯減弱，方位失準角φu在0 s到250 s內振動劇烈，后在250 s處仍存在0.4575°失準角。

隨著海況等級的提高，三軸失準角呈現逐漸增大的趨勢，以五級海況為例，東向失準角的估計誤差為0.0385°，北向失準角的估計誤差為0.0332°，方位失準角的估計誤差為0.3041°，屬于估計誤差范圍內，可認為五級海況位進行速度匹配傳遞對準的最高等級海況。二階巴特沃斯低通濾波器能夠濾去等效桿臂效應引起的加速度計分量，但是無法完全濾去引起的有害加速度，可以采用計算補償法對等效桿臂效應進行補償，計算補償后精度相比卡爾曼濾波、巴特沃斯低通濾波更高且收斂時間更短［12-14］。

3.3.2 計算補償法

卡爾曼濾波中觀測方程選取主子慣導的速度差，但未補償速度差觀察量中桿臂效應速度項，使得桿臂效應速度一直存在影響系統精度。計算補償法通過在速度差觀測量中采取補償桿臂效應速度來提高系統精度。

主子慣導桿臂速度為

主子慣導桿臂速度在導航坐標系中的投影為

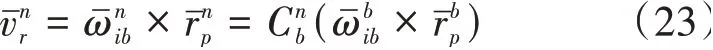
又

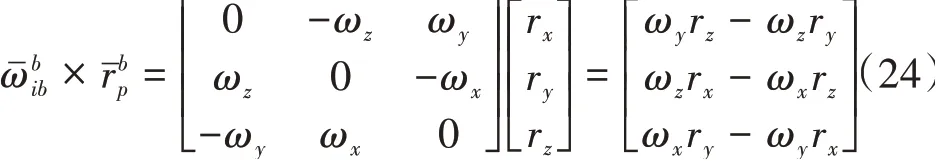
因此

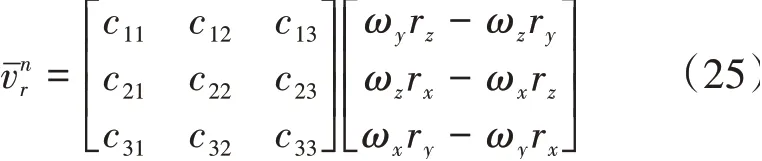
補償掉桿臂效應速度項后，速度誤差觀察量為

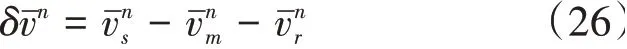
以五級海況為例，對比分析三種濾波方法下不同方向的加速度計輸出波形如圖5所示。（藍線為卡爾曼濾波，紅線為巴特沃斯低通濾波，黑線為計算補償法后的卡爾曼濾波。

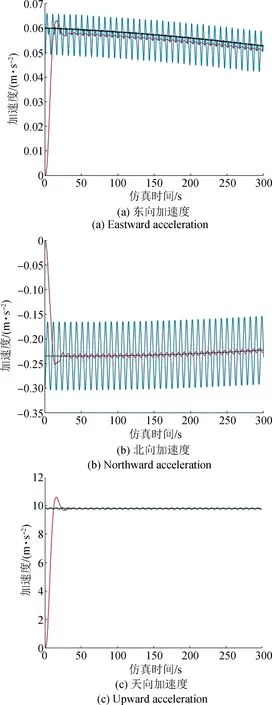
圖5 三種濾波方法下，不同方向的加速度計輸出波形Fig.5 Output waveforms of accelerometers in different directions with three filtering methods

從輸出波形可以看出，計算補償法補償精度和收斂速度相較于卡爾曼濾波和巴特沃斯低通濾波器效果更好，收斂時間更短，整個濾波更為穩定。究其原因，計算補償法要求事先測得桿臂長度，理想條件下計算補償效果更好，如果測量桿臂長度存在較大偏差則結果可能不理想，因此存在局限性。

計算補償法通過嚴格的數學計算在速度差觀測量中采取補償桿臂效應速度，但不能完全補償桿臂效應。

4 結論

針對不同海況等級對傳遞對準桿臂效應影響效果的問題，本文基于分離建模的思想建立船舶六自由度模型，進而建立等效桿臂效應模型，采用三種濾波方法補償桿臂效應，補償結果表明：

1）不同海況等級對傳遞對準產生的桿臂效應不同，海況等級越高，桿臂效應越明顯，越不容易補償，對準精度和對準時間均超過快速對準要求。

2）對比分析三種補償方法：速度匹配傳遞對準采用卡爾曼濾波方法進行濾波不能完全濾去等效桿臂效應誤差，需要進行進一步的補償；采用二階巴特沃斯低通濾波器能使桿臂效應得到收斂，但是失準角仍有進一步的收斂空間，可采用計算補償法對桿臂效應進行補償；計算補償法直接補償主子慣導的速度差，不能完全補償桿臂效應，但其補償精度和收斂速度更好，在具體應用中固定主子慣導空間位置，測量出實際桿臂長度，可以得到更為精確的補償。

3）根據仿真結果分析，五級海況為進行速度匹配傳遞對準的最高等級海況，實際對準低一個海況等級下作為參考，建議實際對準中將四級海況定為傳遞對準最高等級海況。

傳遞對準精度受慣性器件誤差、數據傳輸時延誤差、艦船的撓曲變形和桿臂效應影響，本文考慮桿臂效應影響，后續研究可以綜合考慮誤差情況。