2種飼養模式對番鴨生長和屠宰性能、肉品質的影響
譚東海 雷小文 劉珍妮 鐘云平 謝華亮 孔智偉 陳榮強 吳輝生


摘要:為探討不同飼養模式對番鴨生長性能、屠宰性能和肉品質的影響,選用14日齡公番鴨360羽,隨機分成2組,分別為網上平養組(WP組)和網上墊料組(WD組),每組6個重復,每個重復30羽。在不同飼養模式下,分別測定了各組的生長性能、屠宰性能及胸肌品質。結果表明:(1)WD組的體質量、平均日增質量、平均日采食量和飼料轉化率均高于WP組,但差異不顯著(P>0.05);(2)WD組的心臟指數、肌胃指數和十二指腸厚度均高于WP組,但差異不顯著(P>0.05);(3)WP組的鮮味氨基酸總量、必需氨基酸總量及18種氨基酸總量均顯著或極顯著高于WD組(P>0.05或P>0.01)。由此可見,與網上平養飼養模式相比,網上墊料平養飼養模式不影響番鴨的生長性能和屠宰性能,但對肉質中氨基酸含量有一定的負面影響。
關鍵詞:飼養模式;番鴨;生長性能;屠宰性能;肉品質
中圖分類號: S831.4文獻標志碼: A
文章編號:1002-1302(2021)12-0124-05
收稿日期:2020-10-12
基金項目:江西省現代農業水禽產業技術體系項目(編號:JXARS-09);江西省贛州市科技計劃(編號:贛市財教字[2017]179號)。
作者簡介:譚東海(1986—),男,江西于都人,碩士,畜牧獸醫師,主要從事家禽健康養殖研究。E-mail:1378907729@qq.com。
通信作者:雷小文,碩士,高級畜牧獸醫師,從事動物營養與動物疫病研究。E-mail:343224896@qq.com。
番鴨原產于南美洲,是一種優質的肉用鴨品種,具有較高的瘦肉率和突出的肉質風味特征,受到越來越多消費者和養殖戶的青睞[1]。近年來,網床飼養逐步成為肉鴨養殖的一項主要技術。根據對糞污處理方式的不同,網床飼養又分為網上平養模式和網上發酵床平養模式[2]。網上平養模式的特點是能有效減少動物與糞便接觸的機會,對于防疫、動物機體健康及羽毛質量大有益處[3-4]。但網上平養模式也存在一定弊端,一方面,網墊與番鴨的直接接觸容易影響鴨腿部和腳墊的健康;另一方面,網上平養模式加大了糞污清理和處理的難度,且在造成環境污染的同時增加了處理成本。網上發酵床平養模式可以通過微生物菌群發酵、分解和轉化鴨糞便中的有機質,保護肉鴨腳墊和腿部健康[5],但需要專業技術人員維護菌種,增加了技術難度和養殖成本。鑒于此,本研究嘗試一種全新的番鴨養殖模式——網上墊料平養模式。該模式通過將墊料置于網床上,做到糞尿分離,不僅能夠有效減少番鴨糞便處理成本,也能保持墊料干燥從而減少病原菌孳生,最終減少糞便對番鴨健康的影響。本試驗通過比較網上平養模式和網上墊料平養模式對番鴨的生長性能、屠宰性能、肉品質的影響,為網上墊料平養模式在番鴨健康養殖上奠定理論和科學基礎。
1 材料與方法
1.1 試驗材料
試驗黑羽番鴨(簡稱番鴨)購自江西省于都縣某公司,飼養于江西省贛州市南康區明興養殖場,試驗時間為2020年5—7月。墊料原料(谷殼 ∶木屑=1 ∶1)為贛州市畜牧研究所制備和保存。試驗番鴨基礎日糧的飼料配方及營養水平見表1。
1.2 試驗設計
本試驗采用單因子試驗設計,選擇體質量接近、健康狀態良好的14日齡黑羽公番鴨360羽,隨機分成2組,為網上平養組(WP組)和網床墊料組(WD組),每組180羽(每組6個重復,每重復30羽)。網床墊料養殖是在網上平養的基礎上,添加2層遮陽網,并在遮陽網上鋪2~3 cm墊料。2組的飼料和飼養密度相同:第一階段(14~42日齡),飼養密度為8 羽/m2;第二階段(42~70日齡),飼養密度為4 羽/m2。飼養至70日齡結束,采用常規飼養管理,自由采食和飲水,定期消毒和接種疫苗,網床墊料組在中后期定期添補墊料,2組在試驗結束后清理糞污。
1.3 指標測定與方法
1.3.1 生長性能指標
以重復為單位,每天記錄采食量和死淘數,分別測定21日齡、42日齡、70日齡番鴨體質量。統計14~21日齡,21~42日齡,42~70日齡,14~70日齡各組各重復的采食總量,計算平均日采食量,平均日增質量、料質量比,均參照《NY/T 823—2004家禽生產性能名詞術語和度量統計方法》進行。
1.3.2 屠宰性能指標
試驗結束時(70日齡),每組取6個重復,每個重復取1羽番鴨,進行活體稱質量并記錄數據。參照《NY/T 823—2004家禽生產性能名詞術語和度量統計方法》進行屠宰分割和稱質量,計算屠宰率、半凈膛率、全凈膛率、胸肌率、腿肌率、心臟指數、肝臟指數、脾臟指數、肺臟指數、腎臟指數、法氏指數、肌胃指數、腺胃指數、胰腺指數和十二指腸厚度。
1.3.3 肌肉品質指標
在番鴨70日齡時,每組取6個重復,每個重復取1羽番鴨,屠宰后取100 g番鴨右側胸肌肌肉樣品,將胸肌肉樣送至江西分析測試中心測定肌肉的常規營養成分、氨基酸含量和脂肪酸含量。
1.4 統計與分析
用Excel軟件對數據進行預處理后,采用SPSS 22.0軟件進行單因素方差分析(one-way AMOVA),用Duncans氏法多重比較。結果采用“平均數±標準差”表示。P<0.05表示差異顯著,P<0.01表示差異極顯著。
2 結果與分析
2.1 生長性能
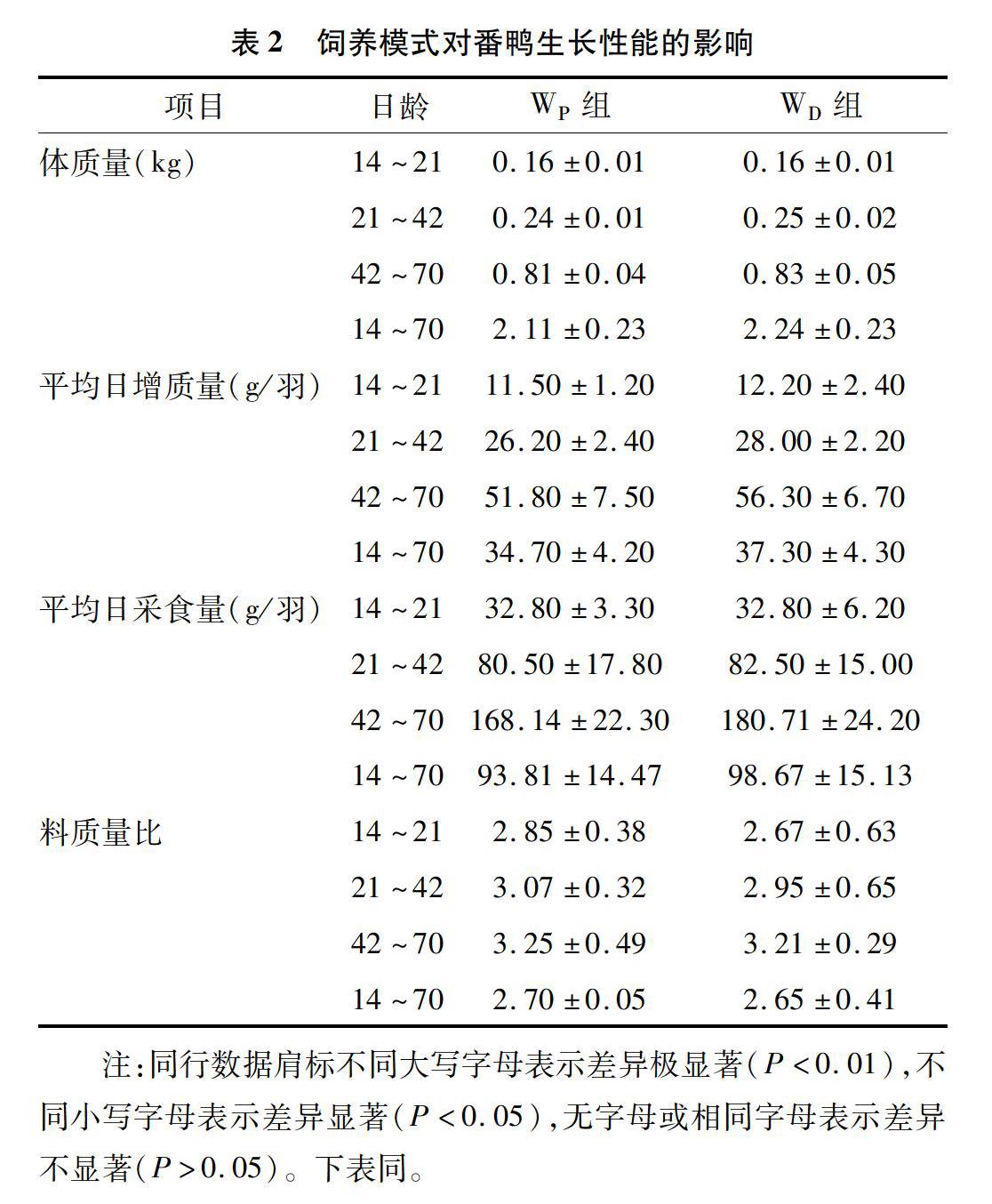
由表2可知,WP組和WD組的體質量、平均日增質量、平均日采食量、料質量比的差異均不顯著。值得注意,在養殖的中后期,WD組的體質量、平均日增質量、平均日采食量均大于WP組,WD組各階段及全程的料質量比均小于WP組。說明在生長性能方面,存在WD組好于WP組的趨勢。
2.2 屠宰性能
由表3可知,2種飼養模式的屠宰性能各指標無顯著差異,但存在WD組的胸肌率、心臟指數、腎臟指數、肌胃指數和十二指腸厚度高于WP組的趨勢。
2.3 肌肉常規營養成分
由表4可知,2組的肉質常規營養成分差異不顯著,但存在WD組的粗脂肪含量高于WP組。
2.4 肌肉氨基酸
由表5可知,天門冬氨酸和18種氨基酸總量WP組極顯著高于WD組(P<0.01);谷氨酸、丙氨酸、纈氨酸、精氨酸和鮮味氨基酸總量WP組顯著高于WD組(P<0.05);其他指標2組差異不顯著。
2.5 肌肉脂肪酸
由表6可知,脂肪酸的各項指標,2組差異均不顯著。但值得注意的是,不飽和脂肪酸總量和必需脂肪酸總量,存在WD組高于WP組的趨勢。
3 討論
3.1 飼養模式對番鴨生長性能的影響
生長性能是衡量家禽品質、飼養水平和屠宰加工效益的重要參考指標,一直以來被廣泛認可[6]。生產性能受諸多因素影響,其中飼養模式是關鍵因素。孫利亞等研究表明,與地面平養相比,網上平養更能發揮家禽的生長性能[7]。張成等研究發現,網上平養番鴨的平均日采食量和平均日增質量顯著高于地面墊料平養[8]。本試驗結果表明,網上平養和網上墊料平養對番鴨的體質量、平均日采食量和平均日增質量及飼料轉化率的影響差異不顯著。本試驗的研究結果與張成等、孫利亞等的研究結果不一致,可能是網上墊料環境優于地面平養環境,不會影響番鴨生長性能的發揮。
3.2 飼養模式對番鴨屠宰性能的影響
屠宰性能是評價家禽品質優劣、飼養管理水平高低和屠宰加工效益情況的重要依據,也是肉品科學需要的基礎資料,全凈膛率是衡量畜禽產肉性能的重要指標之一[9]。一般全凈膛在60%以上,則產肉性能良好[10]。本試驗的2組番鴨的全凈膛率超過以上指標,表明2組的番鴨產肉性能良好。陳長寬等研究發現,網上平養與發酵床對肉雞的全凈膛率、半凈膛率、胸肌率和腿肌率無顯著影響[11]。本試驗結果表明,網上平養和網上墊料平養對番鴨的各項屠宰指標無顯著影響。這與陳長寬等的研究結果相一致,可能網上墊料平養與發酵床環境相似,均具有良好的生長環境,不影響番鴨產肉。
3.3 飼養模式對番鴨胸肌品質的影響
3.3.1 飼養模式對番鴨肌肉中常規營養成分的影響
肉品質的主要決定因素是水分、粗蛋白質和粗脂肪含量;蛋白質是影響肉品營養的主要因素[12-13]。本次試驗結果表明,網上平養與網上墊料平養對番鴨肌肉的常規營養成分無顯著影響。金崇富等研究發現,黃羽肉雞胸肌水分含量、粗蛋白含量發酵床模式顯著高于網上平養[14]。本研究結果與之不一致,可能是由于品種不同和養殖模式的差異導致。本研究結果與陳巖峰等研究的半番鴨網上平養和地面平養的結果[15]相一致。
3.3.2 飼養模式對番鴨肌肉中氨基酸含量的影響
肌肉中氨基酸的含量對肌肉的營養和風味具有重要的決定作用[16-17]。氨基酸分為必需氨基酸和風味氨基酸,肌肉中必需氨基酸含量越高,其營養價值越高,肌肉中風味氨基酸越高,其風味越佳。氨基酸是蛋白質的重要組成部分,因此我們將必需氨基酸含量作為衡量蛋白質的重要指標[18]。本試驗發現,鮮味氨基酸和鮮味氨基酸總量WP組顯著或極顯著高于WD組;必需氨基酸WP組顯著高于WD組;18種氨基酸總量WP組極顯著高于WD組。陳巖鋒等研究發現,網上平養和地面平養對半番鴨肉質中鮮味氨基酸、必需氨基酸和氨基酸總量無顯著影響[16],本試驗結果與之不一致。可能是網上墊料平養與地面墊料平養的養殖環境不同,番鴨在網上墊料上的運動量小,能量消耗少,導致脂肪及脂肪酸含量沉積增加,蛋白質及氨基酸的沉積減少,或是由于番鴨采食了網上墊料進行微生物發酵產生的維生素B12能夠促進肌肉中氨基酸的新陳代謝。美國的相關試驗證實,3倍于通常的B族維生素喂量有利于瘦肉的生長[19]。
3.3.3 飼養模式對番鴨肉質中脂肪酸含量的影響
肌肉中脂肪酸成分和含量是評價其營養價值和風味的重要指標[20]。脂肪酸分為必需脂肪酸、不飽和脂肪酸和風味脂肪酸。有研究表明,不飽和脂肪酸對畜禽及高等哺乳動物均十分重要[21]。王德前等研究發現,肌肉的不飽和脂肪酸對于肉質的風味形成具有重要作用[22]。本研究發現,番鴨肌肉不飽和脂肪酸和必需脂肪酸含量WP組和WD組之間無顯著差異,但存在WD組高于WP組的趨勢。由此說明,單從不飽和脂肪酸和必需脂肪酸含量角度考慮,網上墊料飼養可以提高肌肉中不飽和脂肪酸和必需脂肪酸的含量,間接改善鴨肉的風味和品質,提高了其商品的經濟價值。
4 小結
與網上平養相比,網上墊料平養不會影響番鴨的生產性能、屠宰性能和胸肌肉質中常規營養成分、脂肪酸的含量,但對肉質中氨基酸含量有一定的負面影響。
參考文獻:
[1]鄺春明. 不同飼養模式對種番鴨產蛋性能的影響[J]. 中國家禽,2014,36(8):57,59.
[2]顧麗紅,林哲敏,趙建國,等. 嘉積鴨地面平養、網上平養和網上發酵床平養對比試驗[J]. 黑龍江畜牧獸醫,2018(22):41-44.
[3]Liu B Y,Wang Z Y,Yang H M,et al. Influence of rearing system on growth performance,carcass traits,and meat quality of Yangzhou geese[J]. Poultry Science,2011,90(3):653-659.
[4]Chen Y,Aorigel E,Yan F,et al. Effect of production system on welfare traits,growth performance and meat quality of ducks[J]. South African Journal of Animal Science,2015,45(2):173-179.
[5]張 甜,應詩家,藍賜華,等. 夏季發酵床結合網床養殖模式對舍內環境質量和肉番鴨生產性能的影響[J]. 江蘇農業學報,2016,32(4):860-868.
[6]李文嘉,孫全友,魏鳳仙,等. 飼養方式對北京油雞生長和屠宰性能、肉品質以及肌肉脂肪酸含量的影響[J]. 動物營養學報,2019,31(4):1585-1595.
[7]孫利亞,汪 勇,謝和芳. 飼養方式和低營養水平對5~8周齡肉鵝生長性能和血清生化指標的影響[J]. 動物營養學報,2015,27(3):740-748.
[8]張 成,Hermann A R,陳凱凱,等. 飼養方式對白羽番鴨生長性能、屠宰性能、肉品質及血清生化指標的影響[J]. 揚州大學學報(農業與生命科學版),2017,38(3):44-49.
[9]張 靜,劉 杰,何大乾,等. 網上與地面平養四川白鵝肉質性狀的比較研究[J]. 中國家禽,2013,35(12):33-36.
[10]董福祿,李進軍,屠炳江,等. 太湖鵝屠宰性能和體尺及其相關性[J]. 浙江農業科學,2010(1):167-169.
[11]陳長寬,金崇富,楊智青,等. 發酵床養殖模式下雞生長性狀、肉品質及屠宰性能的研究[J]. 中國農學通報,2019,35(8):102-105.
[12]李 利,臧素敏,王 鵬,等. 太行雞肌肉品質的分析[J]. 動物營養學報,2011,23(9):1592-1599.
[13]Brewer M S,Sosnicki A,Field B,et al. Enhancement effects on quality characteristic of Pork derived from Pigs of various commercial genetic backgrounds[J]. Journal of Food Science,2004,69(1):5-10.
[14]金崇富,楊智青,陳應江,等. 不同養殖模式下黃羽肉雞生長性狀、肉品質及屠宰性能的研究[J]. 江蘇農業科學,2018,46(13):169-171.
[15]陳巖鋒,梁阿政,孫世坤,等. 半番鴨網床平養與地面平養對比試驗[J]. 福建農業學報,2013,28(10):947-952.
[16]Xiang X L,Si S C,Zhao Z T,et al. Effects of polysaccharides from Yingshan Yunwu tea on meat quality,immune status and intestinal microflora in chickens[J]. International Journal of Biological Macromolecules,2020,155:61-70.
[17]陸艷鳳,韓大勇,孫國波,等. 不同飼養方式下黑羽番鴨血清生化指標的比較[J]. 江蘇農業科學,2019,47(2):159-161.
[18]金 融,徐雪梅. 發酵原料在提高肉品質中的應用研究進展[J]. 廣東飼料,2020,29(4):39-41.
[19]孫曉燕,劉志輿. 添加B族維生素喂量有利于瘦肉生長[J]. 國外畜牧學(豬與禽),2002(2):31-33.
[20]金 恒,邱光忠,鐘云平,等. 飼養方式對寧都三黃雞生產性能、肌肉品質、礦物元素含量及血清生化指標的影響[J]. 江蘇農業科學,2020,48(11):180-186.
[21]Givens D I,Gibbs R A,Rymer C,et al. Effect of intensive vs.Free range production on the fat and fatty acid composition of whole birds and edible portions of retail chickens in the UK[J]. Food Chemistry,2011,127(4):1549-1554.
[22]王德前,陳國宏. 影響雞肉品質的主要因素[J]. 中國家禽,2002,24(8):32-33.

