追本溯源，變式拓展
——對(duì)一道教材習(xí)題的“再加工”

文／尹雪蔓

數(shù)學(xué)題目很多，看似變化莫測(cè)，難以招架，其實(shí)不然。縱觀歷年的中考題，雖然年年有新題出現(xiàn)，但萬變不離其宗，這個(gè)“宗”便是教材。

原題呈現(xiàn)（蘇科版數(shù)學(xué)教材九年級(jí)上冊(cè)第92頁第10題）如圖1，AB是⊙O的直徑，AC是⊙O的弦，∠ACB的平分線交⊙O于點(diǎn)D。若AB=10，AC=6，求BC、BD的長。

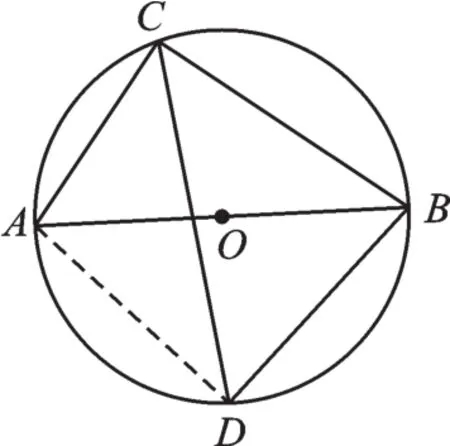
圖1

【解析】連接AD。因?yàn)锳B是⊙O的直徑，所以∠ACB=∠ADB=90°。在Rt△ABC中，根據(jù)勾股定理可得BC=8。因?yàn)镃D平分∠ACB，所以∠ACD=∠BCD=45°。由圓周角性質(zhì)可知∠ABD=∠ACD=45°，故∠BAD=45°，△ABD為等腰直角三角形，進(jìn)而求得BD=5。

【點(diǎn)評(píng)】本題中的一個(gè)關(guān)鍵條件是CD為∠ACB的平分線，也成為我們嘗試變式、拓展探究的條件。

【變式1】如圖2，⊙O的直徑AB為10，弦AC為6，∠ACB的平分線交⊙O于點(diǎn)D，求弦CD的長。

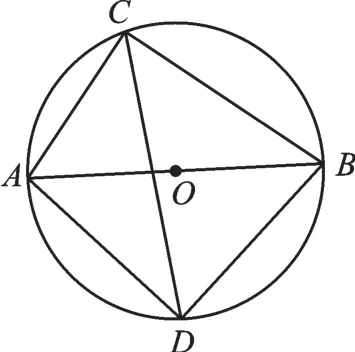
圖2

【解析】直接求CD有難度，可利用∠ACB的平分線這一條件，構(gòu)造等腰直角三角形進(jìn)行求解。

如圖3，過點(diǎn)A作AE⊥CD于點(diǎn)E，易證∠ACD=45°，∴∠CAE=45°，∴AE=CE。

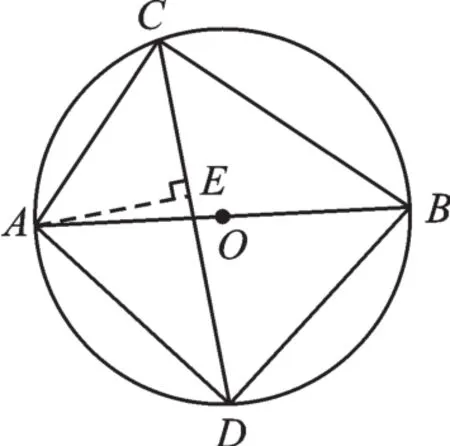
圖3

在Rt△AEC中，AC=6，∴CE=AE=3。

在Rt△AED中，AD=5，∴DE=4。

∴CD=CE+DE=7。

【變式2】如圖4，△ABC內(nèi)接于⊙O，且AB為⊙O的直徑，∠ACB的平分線交⊙O于點(diǎn)D，且AE⊥CD，BF⊥CD，求證：BF=AE+EF。

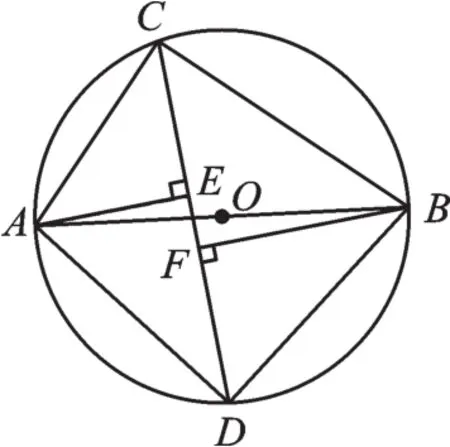
圖4

【解析】易發(fā)現(xiàn)△BCF和△ACE都是等腰直角三角形，

可證BF=CF，AE=CE。

又∵CF=CE+EF，

∴BF=AE+EF。

【點(diǎn)評(píng)】在遇到線段間的和差關(guān)系問題時(shí)，我們常通過尋找相等的線段，將分散的線段轉(zhuǎn)化到同一直線上求解。

【變式3】如圖5，⊙O的直徑AB為10，弦AC為6，∠ACB的平分線交⊙O于點(diǎn)D，過點(diǎn)D作DE⊥BC于點(diǎn)E，求線段DE的長。

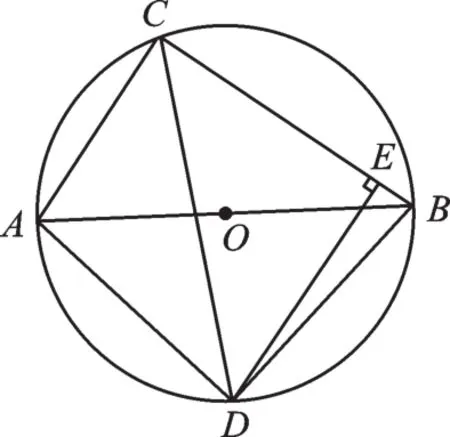
圖5

【解析】易得∠DCE=45°，則△CED是等腰直角三角形。由【變式1】可知CD=7，在等腰直角△CED中，借助勾股定理得DE=7。

【點(diǎn)評(píng)】以上幾種變式的推演主要是利用了角平分線的定義。而如果過點(diǎn)D作角的一邊或兩邊的垂線，則可利用角平分線的性質(zhì)，進(jìn)行如下的探究嘗試。

【變式4】如圖5，△ABC內(nèi)接于⊙O，且AB為⊙O的直徑，∠ACB的平分線交⊙O于點(diǎn)D，過點(diǎn)D作DE⊥BC于點(diǎn)E。猜想線段AC、BC、CE之間的數(shù)量關(guān)系，并加以證明。

【解析】由【變式3】可作一般猜想：AC+BC=2CE。

證明：如圖6，過點(diǎn)D作DF⊥CA，交CA的延長線于點(diǎn)F。

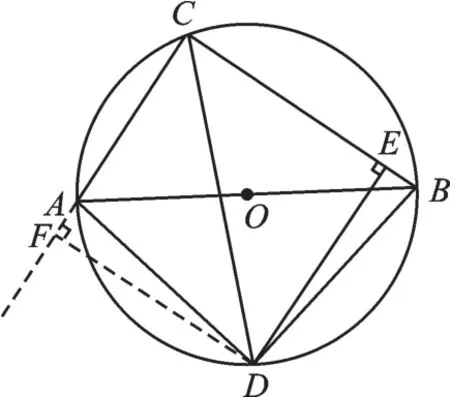
圖6

∵CD平分∠ACB，∴∠ACD=∠BCD，

∴AD=BD。

又∵DE⊥BC，DF⊥CA，∴DE=DF，

∴Rt△AFD≌Rt△BED，

∴AF=BE。

易證四邊形CEDF為正方形，

∴CF=CE，

∴AC+BC=AC+BE+CE=AC+AF+CE=CF+CE=2CE。

【變式5】如圖5，△ABC內(nèi)接于⊙O，且AB為⊙O的直徑，∠ACB的平分線交⊙O于點(diǎn)D，過點(diǎn)D作DE⊥BC于點(diǎn)E，猜想線段AC、BC、CD之間的數(shù)量關(guān)系，并加以證明。

【解析】從【變式1】的計(jì)算結(jié)果得知，AC+BC=14，而CD=7，可猜想AC+BC=CD。證明過程可依據(jù)【變式4】繼續(xù)推演，在此不再贅述。