基于廣義相對論的軌道攝動下星間激光相位比對

梁健，賈前，劉磊,*，唐碩

1. 西北工業大學 航天學院，西安 710072

2. 陜西省空天飛行器設計重點實驗室, 西安 710072

1 引言

地球重力場測量計劃對星間激光測距提出了納米量級的精度要求，如美國NASA提出的GRACE Follow-on計劃，歐洲ESA提出的NGGM計劃以及E. MOTION計劃[1-7]。空間引力波探測計劃提出了皮米量級的星間激光測距精度要求，如NASA和ESA共同提出的LISA計劃以及中國的太極計劃和天琴計劃[7-13]。同時，高精度的星間激光測距有利于提高衛星自主導航和自主定軌精度[14-18]。星間激光高精度相位比對是實現星間納米到皮米量級測距的基礎，在考慮軌道攝動的情況下，需要基于廣義相對論建立更加精確的星間激光相位比對模型[19-20]。

為實現高精度星間測距，一方面可以利用時間比對，另一方面可以利用相位比對。在進行相對論效應校正后，文獻[21]可實現北斗導航衛星Ka波段厘米量級星間雙向測距精度。目前利用激光同步技術可以實現飛秒量級，對應測距精度在亞微米量級[22]。利用時間比對進行星間測距時，即使補償所有系統誤差和路徑誤差，仍然不能滿足納米到皮米量級的空間科學任務需求。

為實現更高精度的星間測距，重力場計劃以及引力波探測計劃都選擇了利用激光相位比對實現星間激光測距。文獻[19]針對GRACE Follow-on計劃，利用程函方程建立星間激光相位比對模型，依據該計劃中的衛星運行軌道高度，對軌道運動影響量級進行了估計，但是未考慮軌道攝動的影響。文獻[20]針對天琴計劃建立星間激光相位比對模型，并根據天琴運行軌道對軌道攝動影響量級進行了估計，但是未考慮軌道攝動引起的軌道變化的影響以及不同軌道時攝動影響的變化趨勢。本文針對地球主引力場范圍內的衛星，研究了軌道攝動對高精度星間激光相位比對的影響，仿真分析得到了軌道高度以及星間距離變化的影響趨勢。

2 星間激光相位比對建模

2.1 時空參考坐標系

選擇GCRS(地心非旋轉坐標系)描述地球衛星運動，廣義相對論下GCRS中的度規張量為[23]：

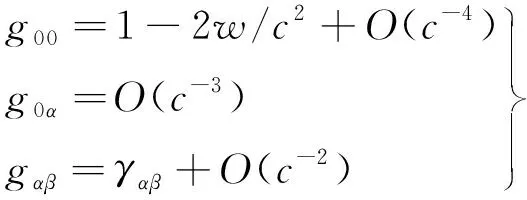
(1)

式中：c為光速；w為引力勢；γαβ=diag[-1 1 1 1]。

對于廣義相對論下四維空間任意兩點之間的距離ds有：

ds2=(cdτ)2=gmndxmdxn

(2)

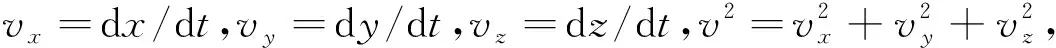
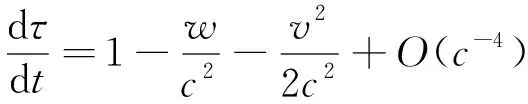
(3)

式中：t為坐標時。上式為基于廣義相對論的GCRS坐標系下原時與坐標時之間的轉換方程。

2.2 星間單向激光相位比對建模

星間激光相位比對如圖 1所示。

圖1 星間激光相位比對示意Fig.1 Schematic diagram of laser phase comparison between satellites

衛星A與衛星B各自搭載一臺超穩激光器，當進行星間激光測距時，衛星A向衛星B發射激光，衛星B將接收到的激光信號與衛星B超穩激光器產生的激光信號進行干涉。衛星A在τA1時刻發射的激光頻率和相位分別為fA(τA1)和φA(τA1)，衛星B在τB2時刻收到的激光相位為φAB(τB2)。此時，可以得到φAB(τB2)=φA(τA1)[24]。

衛星B接收到的激光信號與衛星B超穩激光器產生的激光信號在τB2時刻的相位差為[20]：

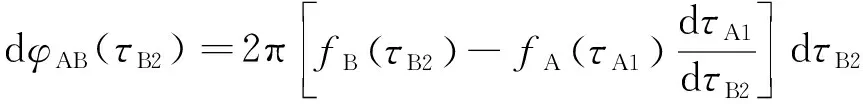
(4)

式中：fB(τB2)為τB2時刻衛星B超穩激光器產生的激光信號頻率。

求解dτA1/dτB2即可得到干涉信號之間的相位差。dτA1/dτB2可改寫為：

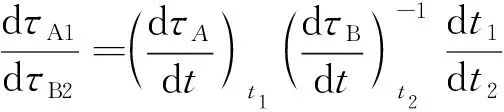
(5)

式中：τA為衛星A的原時；τB為衛星B的原時；t1為對應τA1的坐標時；t2為對應τA2的坐標時。

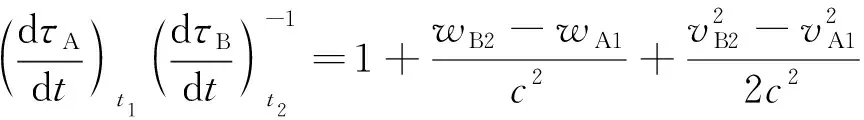
(6)

式中：wB2和vB2分別為τB2時刻衛星B的引力勢和速度；wA1和vA1分別為τA1時刻衛星A的引力勢和速度。

對于t1,t2有：

t1=t2-c-1RAB

(7)

式中：RAB為激光從衛星A發射到衛星B接收的距離。

式(5)中的dt1/dt2可由式(7)求解得到：

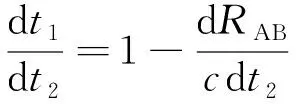
(8)

將式(5)、式(6)和式(8)代入式(4)，并忽略c-2以上的項可以得到：

dφAB(τB2)=2π[fB(τB2)-fA(τA1)]dτB2-

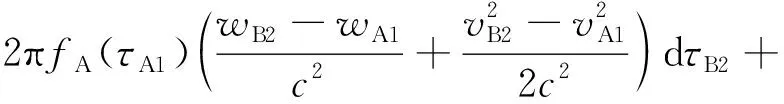
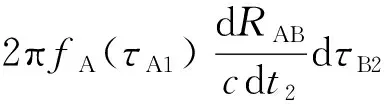
(9)

式(9)為星間單向激光相位比對模型，第2項以及第3項中的Shapiro效應均為廣義相對論效應引起的誤差。

2.3 星間雙向激光相位比對建模

相比于星間單向激光相位比對，在星間雙向激光相位比對中，衛星B將接收到的激光信號利用鎖相器進行鎖相，將鎖相后的激光信號重新發射回衛星A，與衛星A超穩激光器產生的激光信號進行干涉。τA3時刻衛星A接收到的激光相位為φA(τA3)。

衛星B鎖相器對接收到的激光信號進行鎖相時，滿足如下關系[20]：

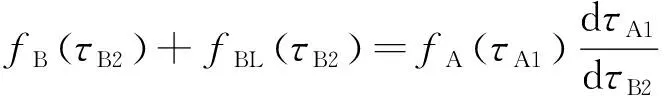
(10)

式中：fBL(τB2)為τB2時刻鎖相器產生的頻率偏移。

由式(10)可以得到衛星A接收到的激光信號與衛星A超穩激光器產生的激光信號在τA3時刻相位差為：

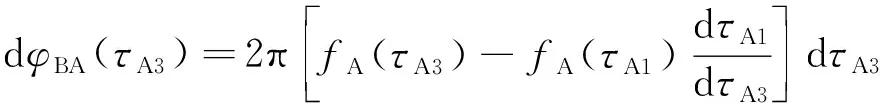
(11)

dτA1/dτA3可改寫為：

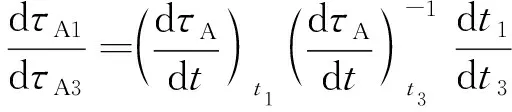
(12)

式中：t3對應τA3的坐標時。

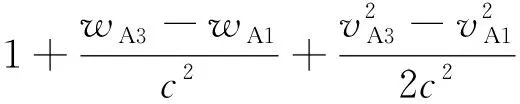
(13)

式中：wA3和vA3分別為τA3時刻衛星A的引力勢和速度；wA1和vA1分別為τA1時刻衛星A的引力勢和速度。

對于t1,t3有：

t1=t3-c-1[RAB+RBA]

(14)

式中：RBA為激光從衛星B鎖相后發射到衛星A接收的距離。

式(12)中的dt1/dt3可由式(14)求解得到:

(15)

將式(12)、式(13)和式(15)代入式(11)，并忽略c-2以上的項可以得到：

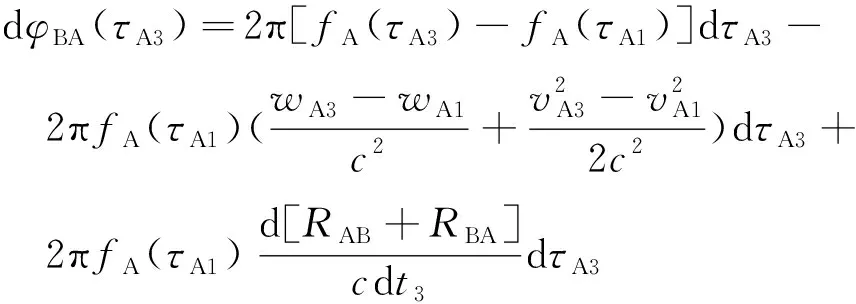
(16)

式(16)為星間雙向激光相位比對模型。

相位比對誤差dφ和距離測量誤差ΔL之間的關系可以表示為：

(17)

式中：λ為激光波長。

3 星間距離變化率

本章將對2.2節星間單向激光相位比對模型和2.3節星間雙向激光相位比對模型中激光比對距離變化率dRAB/cdt2、dRAB/cdt3以及dRBA/cdt3進行求解。

在單向激光相位比對模型中，激光比對距離RAB對衛星B接收時間t2求導，將RAB以接收時間t2表示。考慮Sagnac效應以及Shapiro效應時，激光比對距離可以表示為：

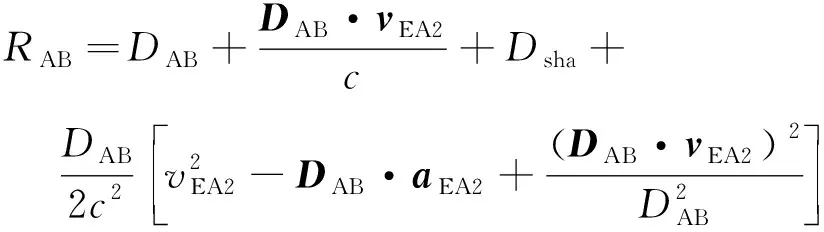
(18)

式中：DAB=rEB2-rEA2；DAB=‖DAB‖；rEB2為t2時刻衛星B在GCRS中的位置矢量；rEA2為t2時刻衛星A在GCRS中的位置矢量；vEA2為t2時刻衛星A在GCRS中的速度矢量；vEA2=‖vEA2‖；aEA2為t2時刻衛星A在GCRS中的加速度矢量；Dsha為廣義相對論中Shapiro效應引起的距離誤差。

對式(18)求導可得：

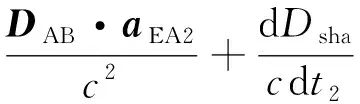
(19)

式中：nAB=DAB/DAB；vAB=vEB2-vEA2。

Shapiro效應是激光受地球引力場的影響產生的距離誤差，可以表示為：

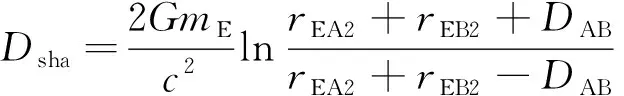
(20)

式中：G為萬有引力系數；mE為地球質量；rEA2=‖rEA2‖；rEB2=‖rEB2‖。

對式(20)求導可得：

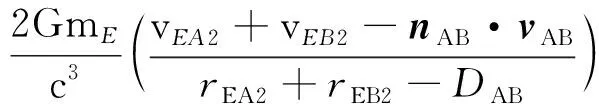
(21)

將式(21)代入式(19)得到距離變化率dRAB/cdt：

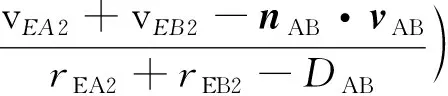
(22)

式(22)中前三項為相對運動引起的幾何距離變化率，最后一項為廣義相對論中Shapiro效應引起的距離變化率。

同理可得距離變化率dRBA/cdt為：

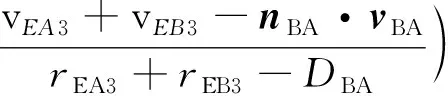
(23)

式中：DBA=rEA3-rEB3；nBA=DBA/DBA；DBA=‖DBA‖；rEB3為t3時刻衛星B在GCRS中的位置矢量；rEB3=‖rEB3‖；rEA3為t3時刻衛星A在GCRS中的位置矢量；rEA3=‖rEA3‖；vBA=vEA3-vEB3；vEB3為t3時刻衛星B在GCRS中的速度矢量；vEB3=‖vEB3‖；vEA3為t3時刻衛星A在GCRS中的速度矢量；vEA3=‖vEA3‖；aEB3為t3時刻衛星B在GCRS中的加速度矢量。

dRAB/cdt3可由式(22)和式(23)聯合求解得到:

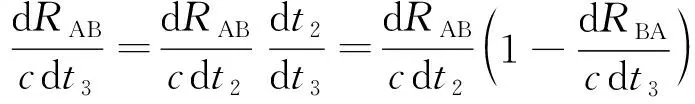
(24)

將式(22)代入式(9)可以得到衛星單向激光相位比對模型的完整表達，將式(23)和式(24)代入式(16) 可以得到衛星雙向激光相位比對模型的完整表達。

4 仿真分析

本章對相位比對模型中影響相位比對精度的因素進行仿真分析。對軌道高度為10 000 km、20 000 km以及36 000 km星間距分別為300 km、3 000 km以及30 000 km的地球軌道衛星進行仿真分析，并在4.3節對仿真結果進行討論。

4.1 單向激光相位比對仿真分析

攝動軌道下，衛星軌道方程為：

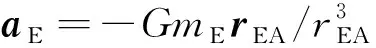
本文主要研究軌道攝動引起的星間激光相位比對中的廣義相對論效應誤差，式(9)中廣義相對論效應誤差為第2項以及第3項中的Shapiro效應，定義式(9)中的廣義相對論效應誤差影響因素為：

σrel=σ1+σ2+σ3

σ1中引力勢考慮地球高階非球形攝動中的J2項可滿足納米到皮米量級星間測距精度要求。

算例：衛星軌道高度為10 000 km，星間距為3 000 km，仿真參數如表 1所示。

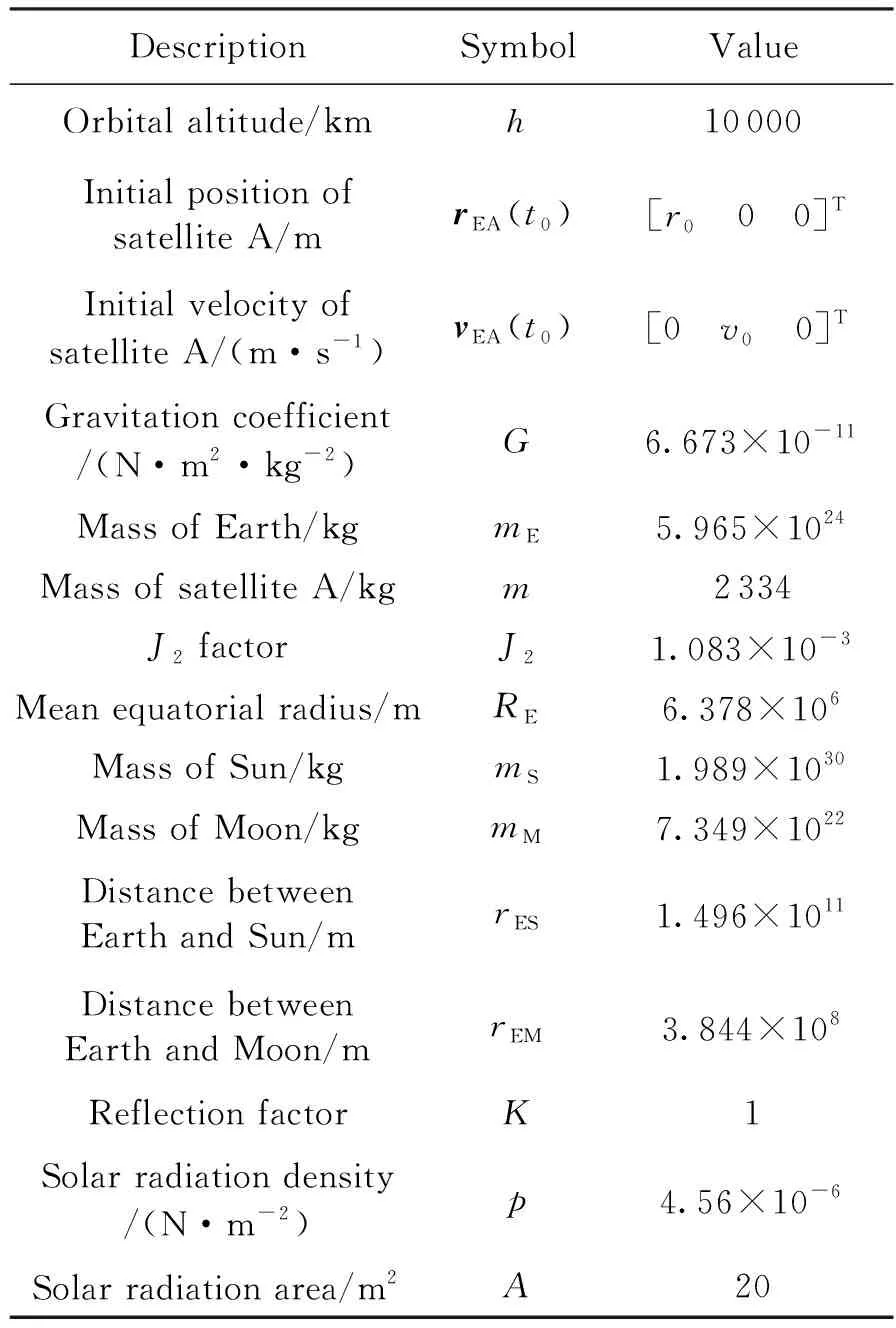
表1 仿真參數

表中：r0=16 371 km，v0=4.930 km/s。衛星B與衛星A軌道高度相同，與衛星A之間的距離為3 000 km，可以得到兩衛星與地心之間的夾角為θ=0.183 430 rad。衛星B的初始位置為[r0cosθ-r0sinθ0]T，初始速度為[v0sinθv0cosθ0]T。仿真時間105s，仿真步長10 ms，仿真結果如圖2所示。

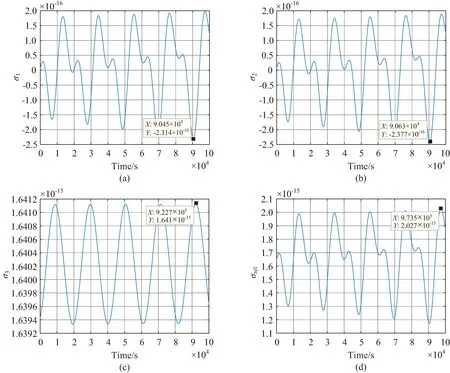
圖2 單向激光相位比對中影響因素曲線Fig.2 Influence factors curves of one-way laser phase comparison

對其他算例分別進行仿真分析，仿真結果如表2所示。

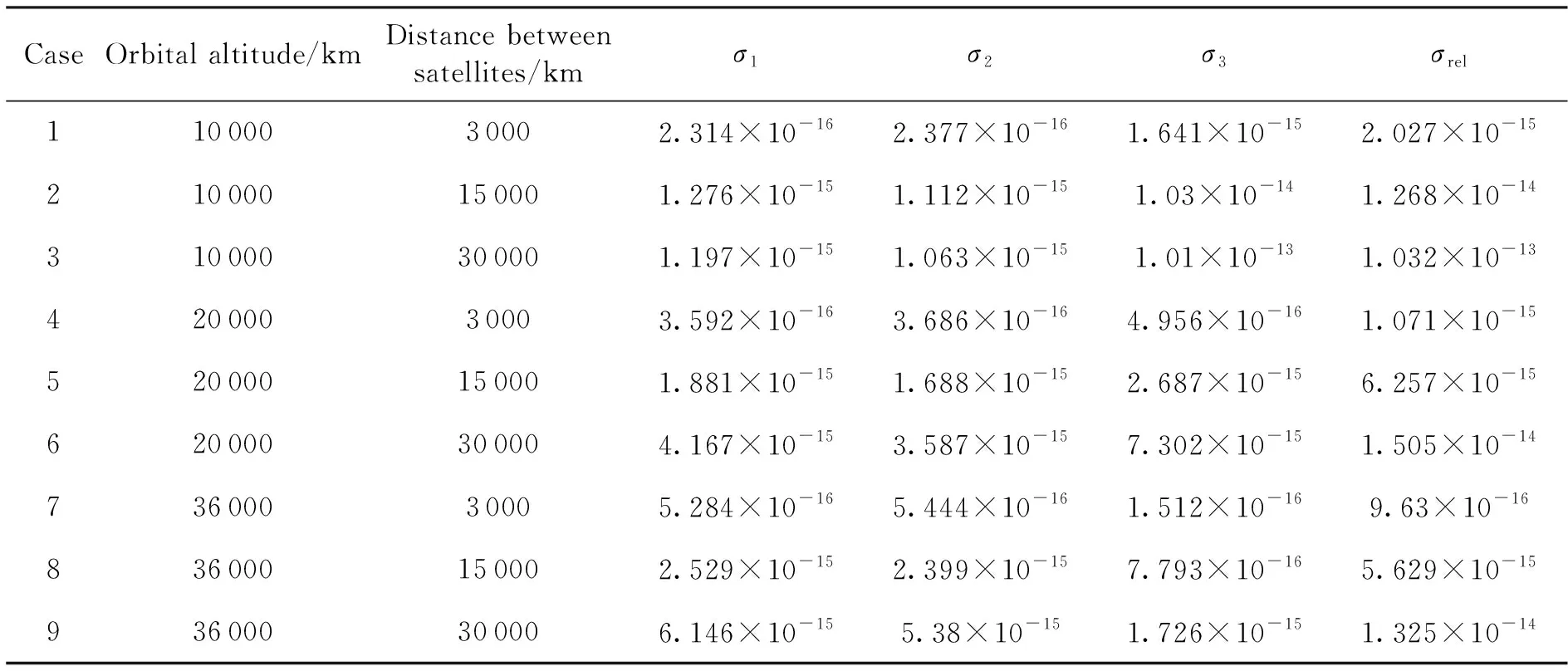
表2 仿真結果匯總1

表中數值為105s仿真時間內σ1、σ2、σ3以及σrel絕對值的極大值。

4.2 雙向激光相位比對仿真分析

雙向激光相位比對中軌道方程和單向激光相位比對相同，同理定義式(16)中的廣義相對論效應誤差影響因素為：

σ3=β1+β2

σrel=σ1+σ2+σ3

算例：衛星軌道高度為10 000 km，星間距為3 000 km，仿真時間105s，仿真步長10 ms，仿真結果如圖 3所示。

對其他算例分別進行仿真分析，仿真結果如表 3所示。

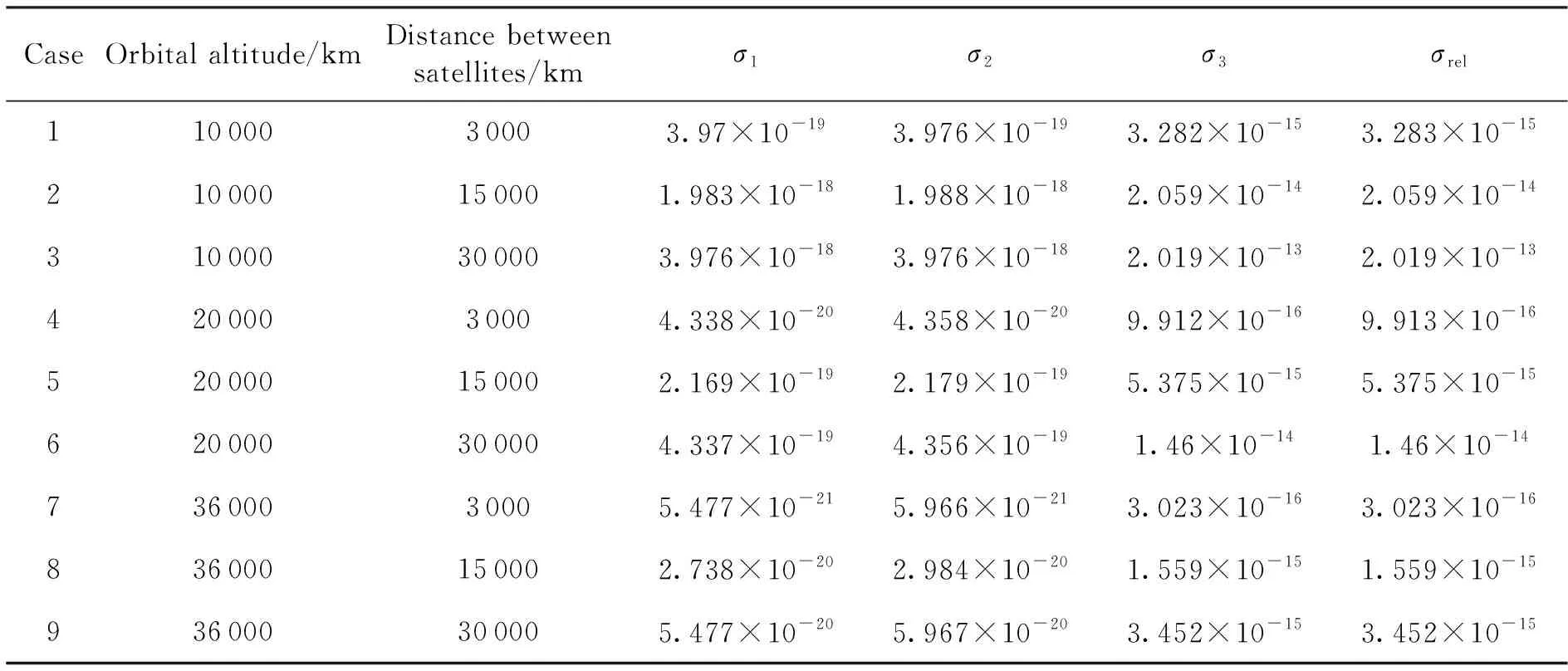
表3 仿真結果匯總2

表中數值為105s仿真時間內σ1、σ2、σ3以及σrel絕對值的極大值。

4.3 結果討論

從表 2和表 3看出，雙向激光相位比對中σ1和σ2遠遠小于單向激光相位比對，σ3為單向激光相位比對的2倍。

從表 2看出，對于衛星單向激光相位比對，σ1和σ2隨軌道高度增高而增大；σ3和σrel隨軌道高度增高而減小。σ3和σrel隨星間距離增加而增大。當θ≤π/2時，σ1和σ2隨星間距離增加而增大；當θ>π/2時，σ1和σ2隨星間距離增加而減小。

軌道高度為10 000 km時，衛星B初始加速度幅值隨夾角θ變化曲線如圖4所示。算例3中θ=2.315 303 rad，由圖4可知衛星B與衛星A之間的初始加速度幅值差小于算例2。因此，算例3中的σ1和σ2分別小于算例2中的σ1和σ2。

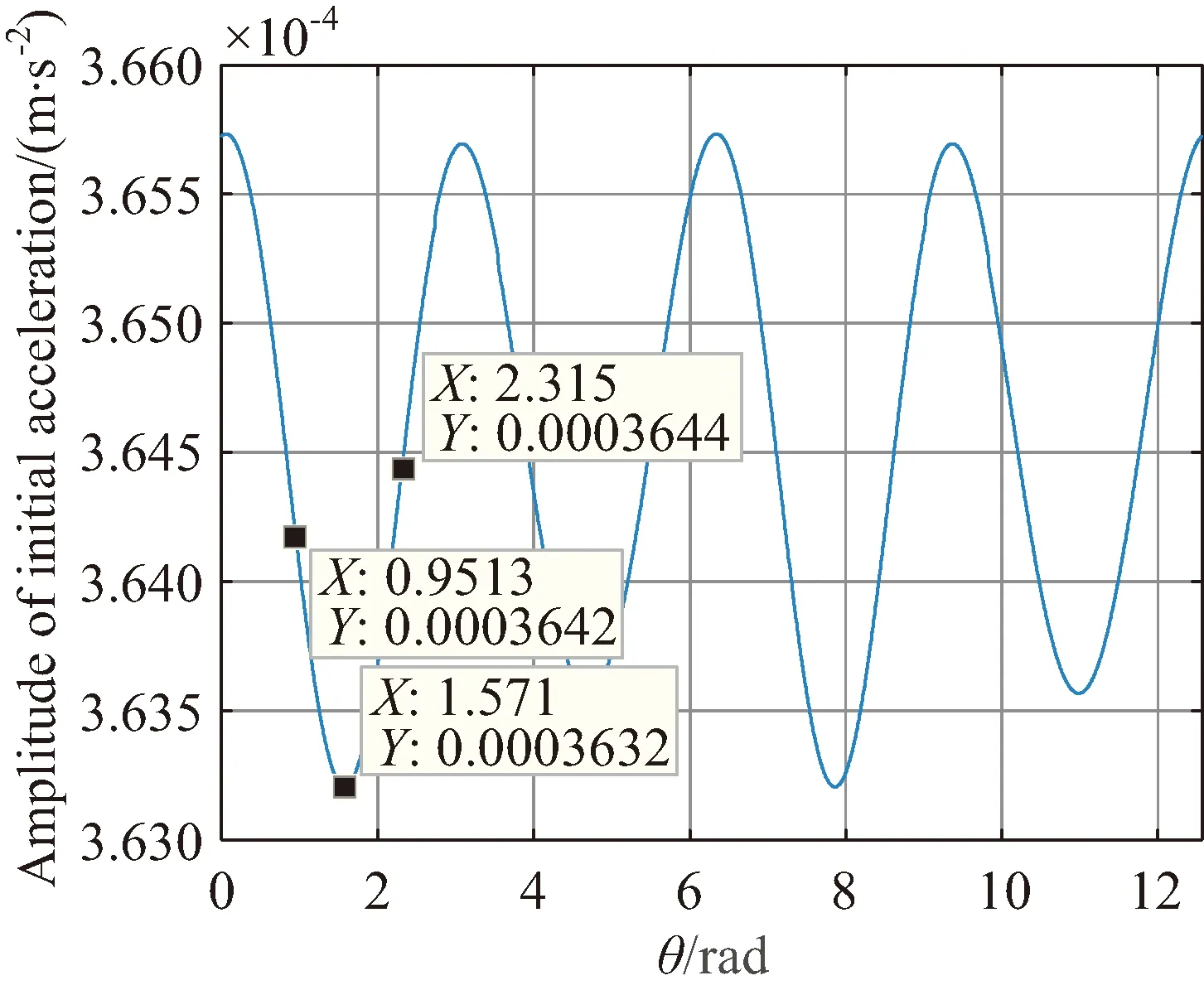
圖4 衛星初始加速度幅值隨夾角θ變化曲線Fig.4 Initial satellite acceleration amplitude graph versus angle θ

從表3看出，對于衛星雙向激光相位比對，σ1、σ2、σ3和σrel隨軌道高度增高而減小，隨星間距離增加而增大。

根據式(17)，由表 2計算得出，對于衛星單向激光相位比對，σ1引起的最大測距誤差為算例9的184.38 nm，σ2引起的最大測距誤差為算例9的161.4 nm，σ3引起的最大測距誤差為算例3的3.03 μm，廣義相對論效應σrel引起的最大測距誤差為算例3的3.096 μm。

由表2計算得出，對于衛星單向激光相位比對，σ1引起的最小測距誤差為算例1的69.42 pm，σ2引起的最小測距誤差為算例1的71.31 pm，σ3引起的最小測距誤差為算例7的45.36 pm，廣義相對論效應σrel引起的最小測距誤差為算例7的288.9 pm。

由表3計算得出，對于衛星雙向激光相位比對，σ1引起的最大測距誤差為算例3的238.56 pm，σ2引起的最大測距誤差為算例3的238.56 pm，σ3引起的最大測距誤差為算例3的12.114 μm，廣義相對論效應σrel項引起的最大測距誤差為算例3的12.114 μm。

由表 3計算得出，對于衛星雙向激光相位比對，σ1引起的最小測距誤差為算例7的3.286 2 fm，σ2引起的最小測距誤差為算例7的3.579 6 fm，σ3引起的最小測距誤差為算例7的181.38 pm，廣義相對論效應σrel引起的最小測距誤差為算例7的181.38 pm。

相比于星間單向激光相位比對，星間雙向激光相位比對減小了除Shpairo效應外的廣義相對論效應測距誤差(對應σ1和σ2)。但是Shapiro效應誤差項 (σ3)放大了兩倍。當星間距較小時(對應本文星間距3 000 km)，基于雙向激光相位比對的星間皮米量級測距，可以忽略除Shpairo效應外的廣義相對論效應測距誤差。經過對仿真結果計算發現，較低軌道時(軌道高度為10 000 km和20 000 km) 單向激光相位比對中軌道攝動引起的廣義相對論效應測距誤差小于雙向激光相位比對；較高軌道時(軌道高度為36 000 km) 單向激光相位比對中軌道攝動引起的廣義相對論效應測距誤差大于雙向激光相位比對。

5 結論

本文針對星間高精度測距的需求，開展地球主引力場衛星間的相位比對研究。分別建立單向和雙向星間激光相位比對模型，并進行仿真分析。不同軌道高度衛星仿真結果表明，軌道攝動引起的廣義相對論效應測距誤差最小為百皮米量級，最大達到微米量級。利用相位比對進行納米到皮米量級高精度測距時，必須考慮軌道攝動引起的廣義相對論效應測距誤差。星間距相同時，軌道高度越高，軌道攝動引起的廣義相對論效應測距誤差越小；軌道高度相同時，星間距越大，軌道攝動引起的廣義相對論效應測距誤差越大。本文工作為空間星間高精度星間測距提供理論支持，對于導航衛星，納米到皮米量級的星間測距精度將大幅提高自主導航精度。