2021年日本東京大學入學考試理科數學試題解析

彭 剛 陳映彤 (廣西師范大學數學與統計學院 541004)

東京大學是日本最頂尖的綜合性大學，匯聚了日本一流的人力資本和學術資源.在日本 近代數學的發展中，東京大學扮演了舉足輕重的角色——1877年日本東京數學會和東京大學 理學部成立，日本現代數學研究正式拉開帷幕.曾獲菲爾茲獎和沃爾夫獎的著名數學家小平邦彥(Kunihiko Kodaira，1915—1997)就曾在東京大學工作過.時至今日，東京大學仍是日本最重要的數學研究機構.

與日本其他著名高校一樣，東京大學每年通過大學入學考試為其選拔大批優秀后備人才，不斷增強本校數學研究的力量.日本著名大學入學考試作為選拔高水平人才的得力方式，其試題的設置方式與內容均值得我們借鑒．本文對東京大學2021年數學入學考試試題進行解析，希望對當前中國實施的“強基計劃”提供參考.

1 試題概述

日本國公立大學的選拔一般由兩場考試構成——學生首先需通過全國統一的大學入學考試，成績合格后才有資格參加國家公立大學自主組織的入學考試

.

東京大學自主組織的入學考試數學試題分為理科卷和文科卷，本文介紹的即為2021年東京大學入學考試中的理科數學試題

.

依據日本最大的教育輔導社河合塾提供的數據，2021年東京大學理科數學試題的總體難度與2020年持平，較2019年有所上升

.

試題中的題目均為解答題，共6大題(每個大題都包含若干個小題)，總分為120分，考試總時長為150分鐘

.

從內容方面來看，這些題目涉及的知識領域包括初等數論、初等代數、解析幾何以及微積分

.

下面我們對這6道問題進行解析

.

2 試題解析

第1題

已知

a

,

b

為實數，平面直角坐標系中有拋物線

C

：

y

=

x

+

ax

+

b

，它與拋物線

y

= -

x

有兩個交點，且兩個交點的橫坐標分別滿足

x

∈(-1,0)，

x

∈(0,1)

.

(1)在平面直角坐標系中表示出點(

a

,

b

)的范圍；(2)在平面直角坐標系中表示出拋物線

C

的范圍

.

解

(1)由得2

x

+

ax

+

b

=0

.

設

f

(

x

)=2

x

+

ax

+

b

，依題意知

f

(

x

)的圖象與

x

軸的兩個交點為(

x

,0),(

x

,0)，且 -1<

x

<0,0<

x

<1

.

由

x

,

x

的分布可知即從而得到平面直角坐標系中點(

a

,

b

)的范圍(如圖1所示，

a

軸上的點除外)

.

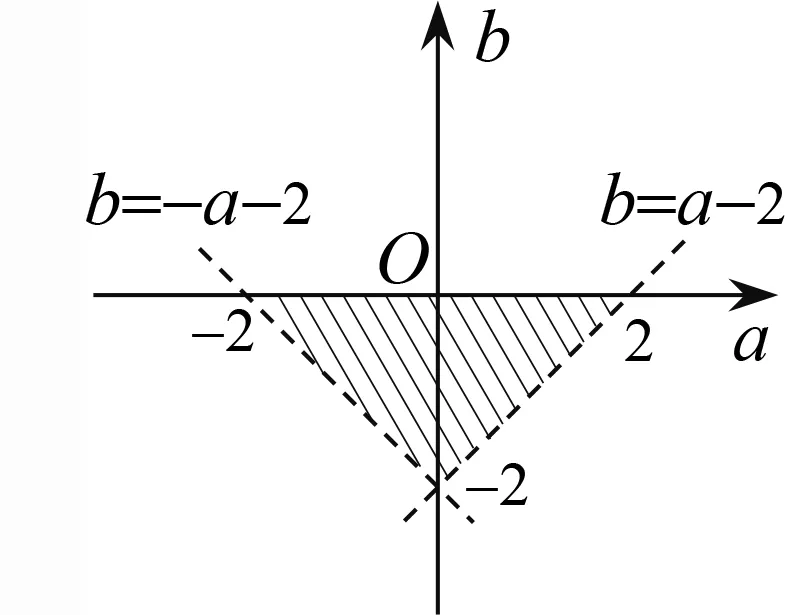
圖1

(2)設(1)中點(

a

,

b

)的范圍為

D

，拋物線通過的范圍設為

E

，(

x

,

y

)為

E

中任意一點，則(

x

,

y

)滿足的條件為：在

xOy

平面上，滿足

y

=

x

+

ax

+

b

且(

a

,

b

)在

D

中；這等價于：在

aOb

平面上，直線

b

=-

xa

+

y

-

x

與

D

有公共點

.

令

g

(

a

)=-

xa

+

y

-

x

，可分為以下四種情況討論：①當-

x

≤-1即

x

≥1時，有所以

x

-2

x

<

y

<

x

+2

x

；②當-1≤-

x

≤0即0≤

x

≤1時，有所以

x

-2<

y

<

x

+2

x

；③當0≤-

x

≤1即-1≤

x

≤0時，有所以

x

-2<

y

<

x

-2

x

；④當-

x

≥1即

x

≤-1時，有所以

x

+2

x

<

y

<

x

-2

x.

綜上可知，

E

的邊界為

y

=

x

-2

x

，

y

=

x

+2

x

，

y

=

x

-2，進一步可得到直角坐標系中

E

的圖形，如圖2

.

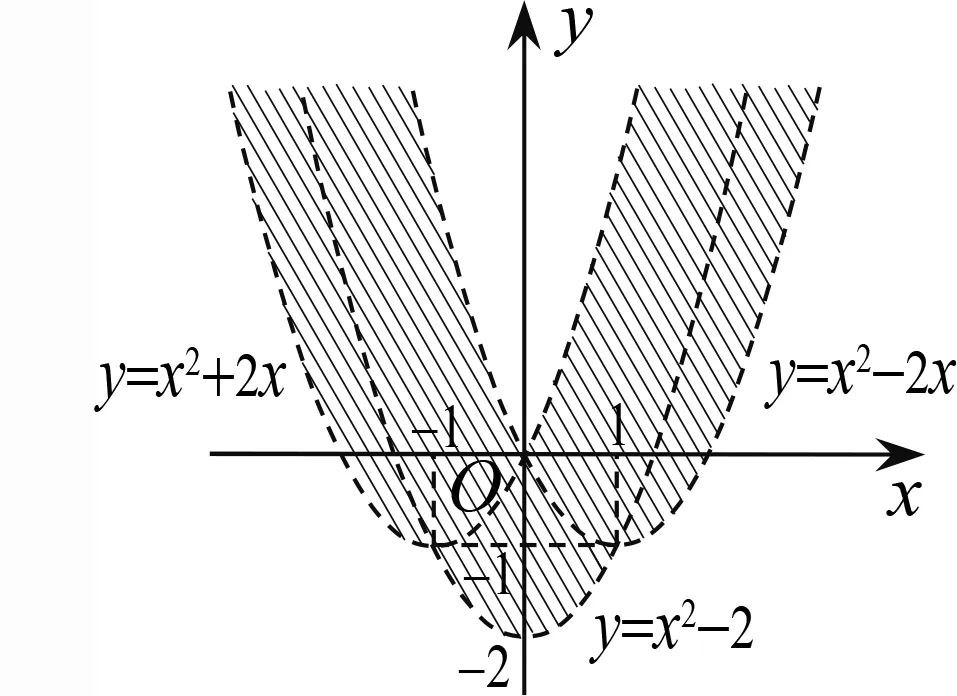
圖2

點評

本題主要考查平面內兩條拋物線的位置關系，內容屬于“解析幾何”，難度層次為“標準”

.

本題分為兩小問，第(1)問較為常規，本質上是關于一元二次方程根的分布問題，解決策略是將其轉換為一元二次函數的圖象與

x

軸的交點情況來處理

.

第(2)問要求動拋物線的移動范圍，此類問題在我國高考和競賽中都較為少見，其解決策略是“反客為主”，把(

a

,

b

)視為動點，從而將動拋物線與定拋物線的相交問題轉化為動直線與定區域的相交問題，具有一定的挑戰性

.

第2題

已知

f

(

z

)=

az

+

bz

+

c

(

a

,

b

,

c

為復數)，i為虛數單位

.

(1)設

α

,

β

,

γ

為復數，且

f

(0)=

α

，

f

(1)=

β

，

f

(i)=

γ

時，請用含

α

,

β

,

γ

的式子表示

a

,

b

,

c

；(2)當

f

(0),

f

(1),

f

(i)均為區間[1,2]中的實數時，請在復平面內表示

f

(2)的范圍

.

解

(1)由題意得即從而解得(2)設

f

(2)=4

a

+2

b

+

c

=

ω

，將(1)的結果代入

f

(2)中，有=

α

(-1-2i)+

β

(3+i)+

γ

(-1+i)，其中，

α

,

β

,

γ

是滿足1≤

α

≤2，1≤

β

≤2， 1≤

γ

≤2的實數

.

設-1-2i=

z

,3+i=

z

,-1+i=

z

，則當1≤

α

≤2且1≤

β

≤2時，由復數加法的幾何意義可知，

αz

+

βz

的范圍為一個平行四邊形(圖3)

.

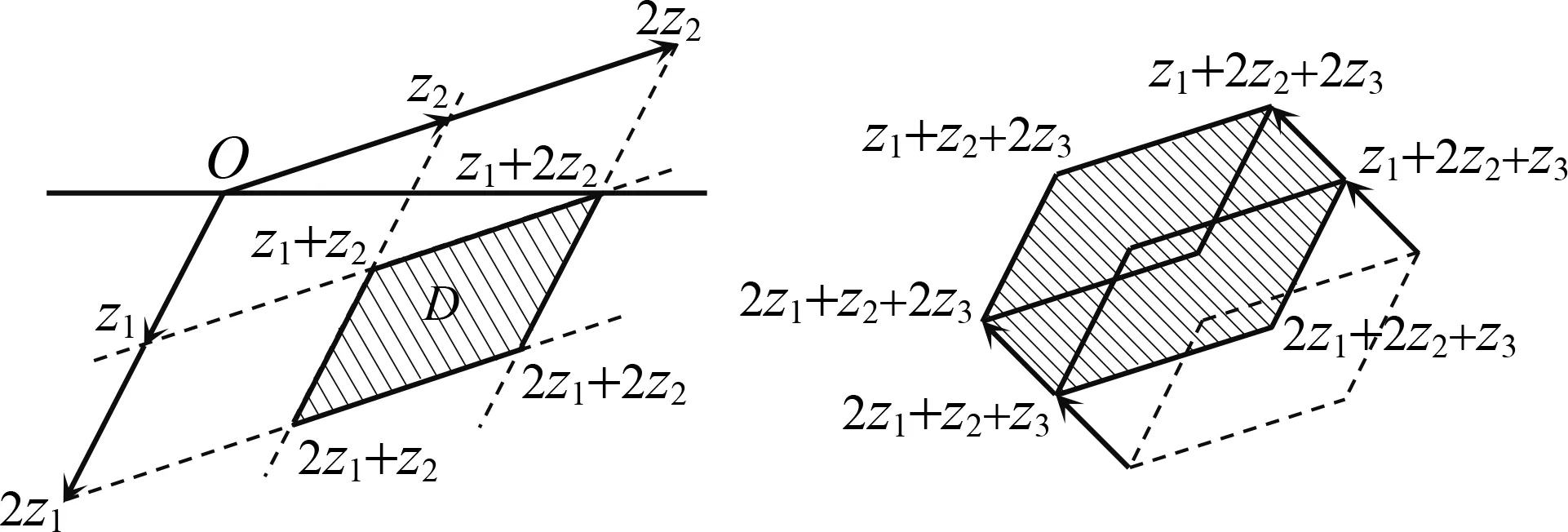
圖3 圖4

假設這個平行四邊形的邊界及內部為

D

，

D

中的各點再加上

γz

(1≤

γ

≤2)，便可得到

ω

即

f

(2)的范圍(圖4)

.

點評

本題主要考查復數的運算及其幾何表示，內容屬于“初等代數”，難度層次為“較難”

.

本題有兩問，第(1)問求

a

,

b

,

c

的表達式，為常規計算

.

第(2)問求

f

(2)的范圍，涉及三個變量，難度較大；此問的解題策略是“逐步推進”——先研究兩個變量的情況，然后在此基礎上研究三個變量

.

就表達方式而言，求解第(2)問時既可以利用復數加法的幾何意義，也可以轉換成向量的加法，二者本質上是相通的

.

第3題

已知函數的圖象為

C.C

在點

A

(1,

f

(1))處的切線為

l

：

y

=

g

(

x

)

.

(1)若

C

與

l

只存在一個與點

A

不同的交點，求該點的橫坐標；(2)設(1)中交點的橫坐標為

α

，求定積分

解

(1)由知又所以

l

的方程為令

g

(

x

)=

f

(

x

)，即解得

x

=

x

=1,

x

=-3

.

因此

C

與

l

異于

A

的交點為(-3，

g

(-3))，因此所求的橫坐標為-3

.

(2)由題意

令容易得到

下面使用換元法來計算

I

和

I

.

令則從而有

綜上可知

點評

本題主要考查切線方程求解及定積分的計算，屬于“微積分”的內容，難度層次為“標準”

.

本題中的求導運算和積分運算均比較常規，但對計算的準確性提出了較高的要求

.

第4題

回答以下問題：(1)若正奇數

K

,

L

和正整數

A

，

B

滿足

KA

=

LB

，且

K

與

L

除以4的余數相同，證明：

A

與

B

除以4的余數也相同；(2)正整數

a

,

b

滿足

a

>

b

，令證明：存在正奇數

K

,

L

滿足

KA

=

LB

；(3)

a

,

b

滿足(2)中條件，且

a

,

b

同奇偶，證明：與除以4的余數相同；(4)求除以4的余數

.

解

(1)由于4|(

K

-

L

)，令

K

-

L

=4

n

(

n

為整數)，則

K

=

L

+4

n

．又

KA

=

LB

，故(

L

+4

n

)

A

=

LB

，即

L

(

A

-

B

)=-4

nA

，而

L

為奇數，所以

A

-

B

是4的倍數，從而得到

A

與

B

被4除的余數相同

.

(2)依題可知，

令

r

=4

a

(4

a

-4)·…·(4

a

-4

b

+4)，

r

=(4

a

+1)(4

a

-3)·…·(4

a

-4

b

+1)，

r

=(4

a

-2)(4

a

-6)·…·(4

a

-4

b

+2)，

r

=(4

a

-1)(4

a

-5)·…·(4

a

-4

b

+3)，以及

t

=4

b

(4

b

-4)·…·8·4，

t

=(4

b

+1)(4

b

-3)·…·5·1，

t

=(4

b

-2)(4

b

-6)·…·6·2，

t

=(4

b

-1)(4

b

-5)·…·7·3，

高級氧化模塊又稱做深度氧化模塊，在高溫高壓、電、聲、光輻照、催化劑等反應條件下，產生具有強氧化能力的羥基自由基(·OH)，使大分子難降解有機物氧化成低毒或無毒的小分子物質的修復模塊。高級氧化模塊具有處理效率高，泛用性好，體積小等優點，廣泛應用于各種污染場地地下水處理。西玖環保通過多年經驗積累，對高級氧化模塊處理工藝進行優化，達到業內較高的處理效率和設備壽命。一套設備可以拆卸成多個模塊運輸到下一個污染場地繼續使用，有效降低地下水處理成本，大大提高了資源利用率。

則有從而得到

令

L

=

r

r

(2

a

-1)(2

a

-3)·…·(2

a

-2

b

+1)，

K

=

t

t

(2

b

-1)(2

b

-3)·…·3·1，此時

K

,

L

均為正奇數，且滿足即有

KA

=

LB.

(3)易知

r

≡

t

(mod 4)，

r

≡

t

(mod 4)，又2|(

a

-

b

)，故4|(2

a

-2

b

)，即2

a

≡ 2

b

(mod 4)，從而有(2

a

-1)(2

a

-3)·…·(2

a

-2

b

+1)≡(2

b

-1)(2

b

-3)·…·(2

b

-2

b

+1)=(2

b

-1)(2

b

-3)·…·3·1(mod 4)．因此

K

≡

L

(mod 4)，結合(2)的結論便可得到(4)由(3)可知所以除以4的余數為3

.

點評

本題主要考查整除和同余理論，內容屬于“初等數論”，難度層次為“較難”

.

本題共有4個小問，并且它們環環相扣，問題的設計很精妙

.

本題引入了組合數，因而增加了題目的難度，解題者需要根據(1)中的結論，將組合數展開中的諸多整數按照模4的余數進行分類，并通過換元來簡化運算，具有很強的技巧性

.

第5題

已知

α

為正實數，關于

θ

的函數

f

(

θ

)為平面上

A

，

P

兩點距離的平方，這兩點的坐標分別為

A

(-

α

，-3)，

P

(

θ

+sin

θ

,cos

θ

)(0≤

θ

≤π)

.

(1)證明：當0<

θ

<π時，存在唯一的

θ

使得

f

′(

θ

)=0；

解

(1)依題可知

f

(

θ

)=

AP

=(

θ

+sin

θ

+

α

)+(cos

θ

+3)，則

f

′(

θ

)=-4sin

θ

+2(

θ

+

α

)cos

θ

+2(

θ

+

α

)，

f

″(

θ

)=-2(

θ

+

α

)sin

θ

-2cos

θ

+2，

f

?(

θ

)=-2(

θ

+

α

)cos

θ.

由

f

?(

θ

)的正負可得到

f

″(

θ

)的單調性，如下表所示：

θ00,π2 π2π2,π πf?(θ)-0+f″(θ)0↘2-π-2α↗4

因為所以存在使得

f

″(

β

)=0．又

f

″(

θ

)在內單調遞增，故這樣的

β

是唯一的

.

由

f

″(

θ

)的正負繼續可以得到

f

′(

θ

)的單調性，如下表所示：

θ0(0,β)β(β,π)πf″(θ)-0+f'(θ)4α↘f'(β)↗0

因為

f

′(

θ

)在(

β

,π)內單調遞增，所以

f

′(

β

)<

f

′(π)=0，而

f

′(

θ

)在(0,

β

)內單調遞減，且

f

′(0)=4

α

>0，所以在(0,

β

)中存在唯一一個

γ

使得

f

′(

γ

)=0

.

(2)由

f

′(

θ

)的正負可以得到

f

(

θ

)的單調性，如下表所示：

θ0(0,γ)γ(γ,π)πf'(θ)+0-0f(θ)f(0)↗f(γ)↘f(π)

從上表容易看出

f

(

θ

)的最大值為

f

(

γ

)，依題意有從而得到即-4解得

α

的范圍為

點評

本題主要考查零點定理、函數的導數與函數的單調性之間的關系，屬于“微積分”的內容，難度層次為“標準”

.

本題有兩小題，其中第(1)題十分有特色，解答過程中涉及多個存在性問題

.

與第3題主要考查計算不同，本題帶有濃厚的“分析”味道，解題者既需要清晰的邏輯思維，又需要有較強的直覺能力

.

第6題

已知

b

,

c

,

p

,

q

,

r

為常數，下式為關于

x

的一個恒等式：

x

+

bx

+

c

=(

x

+

px

+

q

)(

x

-

px

+

r

)

.

(1)當

p

≠0時，用

p

,

b

表示

q

,

r

；(2)當

p

≠0時，設(

a

為常數)，請寫出一組滿足[

p

-(

a

+1)][

p

+

f

(

a

)

p

+

g

(

a

)]=0的有理系數整式

f

(

t

)與

g

(

t

)；(3)若

a

為整數，關于

x

的四次多項式可分解為二次有理系數多項式的乘積，求

a.

解

(1)由

x

+

bx

+

c

=(

x

+

px

+

q

)(

x

-

px

+

r

)=

x

+(

q

+

r

-

p

)

x

+

p

(

r

-

q

)

x

+

qr

知當

p

≠0時，有(2)當

p

≠0時，由可得即

p

-4

cp

-

b

=0

.

將代入上式得到

p

+(4

a

+3)(

a

+1)

p

-(

a

+1)(

a

+2)=0，從而有[

p

-(

a

+1)][

p

+(

a

+1)

p

+(

a

+1)(

a

+2)]=0

.

故滿足條件的一組整式

f

(

t

)與

g

(

t

)為

f

(

t

)=

t

+1，

g

(

t

)=(

t

+1)(

t

+2)

.

(3)令其中

p

,

q

,

r

均為有理數

.

①當

p

=0時，

P

(

x

)=(

x

+

q

)(

x

+

r

)=

x

+(

q

+

r

)

x

+

qr

，此時有易知

a

=-2，

r

=-

q

，從而有這與

q

是有理數矛盾

.

②當

p

≠0時，由(2)知

p

滿足[

p

-(

a

+1)][

p

+(

a

+1)

p

+(

a

+1)(

a

+2)]=0，由于

p

+(

a

+1)

p

+(

a

+1)(

a

+2)恒大于0，所以

p

-(

a

+1)=0，即又當

p

為有理數時，

q

,

r

均為有理數，故只需為有理數即可

.

令(

m

,

n

為互質的正整數)，則有

m

(

a

+1)=

n

．由于

a

為整數，所以

m

整除

n

.

由于

m

,

n

互質，所以

m

,

n

也互質，從而有

m

=1，即

m

=1，此時有

a

+1=

n

，所以(

a

+

n

)(

a

-

n

)=-1，解得當

a

=0時，

點評

本題主要考查代數式的運算，內容屬于“初等代數”，難度層次為“較難”

.

本題具有較強的綜合性，解題步驟也較多，對解題者的計算準確性要求很高．此外，本題涉及較多的字母(除了主元

x

外，還有6個表示常量的字母

a

,

b

,

c

,

p

,

q

,

r

)，因而解題者需要具備較強的信息處理能力

.

3 結語

2020年1月，中國教育部頒布文件《關于在部分高校開展基礎學科招生改革試點工作的意見》．該文件聚焦國家重大戰略需求，決定從2020年起取消高校自主招生考試，在試點的36所高校實施“強基計劃”，以提升基礎學科人才選拔和人才培養質量．

通過對中國2020年“強基計劃”中部分大學的試題與東京大學的入學試題的對比，不難發現兩國的試題各具特點．中國實施“強基計劃”的部分著名高校試題題目數量較多，比如北京大學和清華大學的試題都是20道，復旦大學的試題有33道，并且題型均為選擇題，因而考查的知識面比較廣；而東京大學的自主招生考試題目較少，但均為解答題，因而能更深入地考查學生的數學思維和數學表達能力．此外，東京大學入學試題對微積分這一內容的要求很高；事實上，微積分這一內容是日本各大高校入學考試中的重要考查對象，相對而言我國的高校在這方面則要求不高．東京大學等日本頂級大學的入學數學試題為當前中國數學資優生的培養與選拔提供了重要參考．