基于改進TOPSIS的道路交通風險網絡排序研究

戴劍勇，黃曉慶，王雯雯

(1. 南華大學 資源環境與安全工程學院，湖南 衡陽 421001；2. 南華大學 核設施應急安全作業技術與裝備湖南省重點實驗室，湖南 衡陽 421001)

0 引 言

據2019年中國統計年鑒記錄，2019年我國交通事故發生次數為244 937次，死亡人數為63 194人，道路交通事故致死在非正常死亡中占比越來越重。定量分析各風險在系統中所起的作用以及關鍵程度，能夠有側重地應對風險，有效提高風險管理效率，減少道路交通事故發生的重復性。

在這之前，眾多學者對道路交通事故機理進行了研究分析。陳丹[1]從駕駛員、車輛、管理、道路等方面研究了高速公路交通事故致因；WU Yina等[2]分析了大霧天氣下道路交通特性的變化和碰撞風險；在風險排序和提取關鍵風險方面，WU Bo等[3]應用TOPSIS、灰色關聯度等分析方法對影響隧道穩定性的因素進行排序；BAHRAMI S等[4]運用TOPSIS方法對配電饋線進行優先排序，為檢修分配提供依據；WU Jianjun[5]、花玲玲等[6]、王靈麗等[7]從復雜網絡理論出發分別分析了道路碰撞、鐵路事故、交通線路網絡需要防控的關鍵節點。

復雜網絡分析節點重要性是根據網絡特性指標判斷，但每一個指標的側重點都有所不同，需要對其進行綜合的分析。筆者擬采用已經在鐵路等[8]領域被應用的人因分析與分類系統(HFACS)[9]對事故風險進行分析、分類。而后結合復雜網絡指標，建立PPR方法[10]賦予指標權重的優劣解距離法(TOPSIS)[11]以消除傳統TOPSIS方法主觀性較強，與網絡結合不緊密的缺陷，對風險進行綜合排序，實現對道路交通關鍵風險的識別，根據風險重要度排序確定合理應對風險的分配方案，更高效的控制風險。

1 道路交通網絡風險分析及模型構建

1.1 道路交通網絡安全風險因素分析

將該模型與道路交通系統融合，在HFACS原模型基礎上進行改進(圖1)，可分為組織影響、不安全監督、不安全狀態、不安全行為四大類，四大類下又各有子類，這4層分類由上到下施加影響[12]，分為圖中陰影部分為修改項。

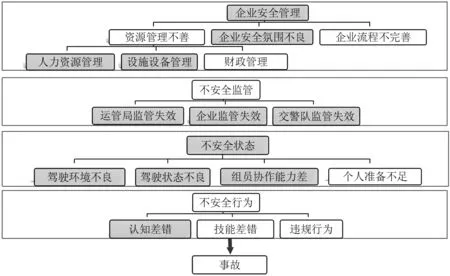
圖1 道路交通HFACS分類框架Fig. 1 HFACS classification framework of road traffic

1.2 道路交通網絡風險模型構建

道路交通網絡是由眾多節點和節點之間的連線組成的拓撲結構模型，道路交通安全中的安全風險之間能夠相互影響，具有較為復雜的相互作用關系，對于道路交通系統安全風險網絡做出以下設定，并構建網絡。

設定1交通事故風險是抽象的，現將風險和風險間的相互作用用網絡呈現出來，設定風險為節點，風險間的相互關系為連邊，便能初步構成無向網絡。

設定2考慮到交通風險間的作用是單向的，風險的傳播是層層遞進的，考慮到有向網絡對事故風險間作用的描述更精準，故進一步將連邊設定為有向的。

設定3假設指向某一安全風險的其他風險對該安全風險的作用相同，即網絡中各風險之間的連邊權重為1，不對它們之間的作用力進行區分。

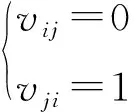
2 道路交通網絡安全風險排序

2.1 道路交通網絡風險排序指標

1)度中心性。該參數在道路交通風險網絡中就是指與某風險相關聯的風險個數，在網絡中具象為連邊數。邊數越多表示該風險在網絡中關聯度越大。筆者定義為：

(1)

2)接近中心性。該參數描述的是特定風險到與除特定風險以外的所有風險的平均距離值，當某風險的值越大，表示該風險與其他風險的聯系越緊密。其表達式為：

(2)

式中：L為與風險i相連的風險集合；dij為風險i到j的最短路徑值，即風險i到j最少路徑的數量。

3)介數中心性。風險節點的介數指在一個網絡中所有最短通行路徑中經過該風險的總數量比率，反映相應風險對于整個網絡的作用和影響能力，數值越大，表明該風險對道路交通事故的影響越大。定義為：

(3)

式中：nfh為風險f和風險h之間的最短通行路徑數量；nfh(i)為風險f和h之間的最短通行路徑經過節點的數目。

2.2 PPR-TOPSIS綜合排序

在傳統的TOPSIS方法中，最初賦予的權重值依賴于專家的主觀判斷。而PPR-TOPSIS方法權重是根據網絡中心性指標和PPR方法計算得出的。計算3個中心性指標權重的核心是根據每個指標不同的節點排序賦予3個指標中的節點不同的初值，組成不同的初值向量，再分別對3個指標進行PPR分析，根據最終落在事故節點上的概率定量化3個指標對事故造成的影響的大小作為權重。如此，通過計算得到客觀的權重值，構建權重矩陣，再對所有節點進行綜合排序。

2.2.1 PPR法確定各指標權重

1)確定風險初值向量：根據指標中的節點排序給予每個指標中的節點不同的初值。將指標中的風險初值按比例縮放使得和為1，得到每個風險標準值記為Pv，各風險標準值組成的向量表示為Pr0={P1,P2,P3,…,Pv}。

2)確定風險跳轉概率：風險發生后每一時間步可能游走的路線數目，在復雜網絡中可具象為該節點的出度值，每個節點到其他節點的跳轉概率組成整個網絡的轉移概率矩陣P為：

(4)

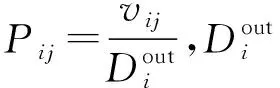
3)確定各指標權重值：3種指標下，各指標中風險初值不同，那么最終對各節點的影響概率Pr不同。Pr值由式(5)迭代得到：

(5)

式中：α為阻尼系數，0≤α≤1，一般取0.85，取3種指標各自迭代完成后的事故節點Pr值，歸一化指標值，得到各指標權重wD，wC，wB。

2.2.2 TOPSIS綜合排序

將各指標中標準化后的節點值分別作為列向量，組成規范化決策矩陣Y，由于已經應用PPR方法賦予了各指標權重，即可按元素zij=w×y寫出加權規范矩陣為：

(6)

式中：d、c、b分別為點度、接近、介數中心性標準化后的值。

由于3個中心性指標都為效益型指標，根據矩陣Y可以確定正理想方案Z+以及負理想方案Z-：

(7)

根據式(8)～式(9)得到各個方案Z到正理想方案Z+以及負理想方案Z-之間的歐式距離為：

(8)

(9)

計算以上理想方案的貼近度Ti，按照Ti的大小進行交通風險的重要度排序，值越大的風險對事故的影響越大。貼近度計算公式為：

(10)

3 實例分析與討論

2018年，京港澳高速公路衡陽段，一起客車與載有危化品的重型罐車相撞的重大道路交通事故造成了18人死亡，14人受傷，直接經濟損失達2 632.8萬元。這起事故涉及部門和人員眾多，是一起典型的道路交通事故，能夠一定程度上反應大部分道路交通事故情形，以此為例構建復雜網絡進行分析，論證上述方法的可行性，同時獲取該起事故風險的綜合重要度排序，為相關部門提供參考，避免這類事故再次發生。

3.1 “6·29”重大道路交通事故模型構建

3.1.1 事故風險分類

研究了該事故的事故調查報告[13]后，運用HFACS模型對該起事故的安全風險進行了分類(表1)。

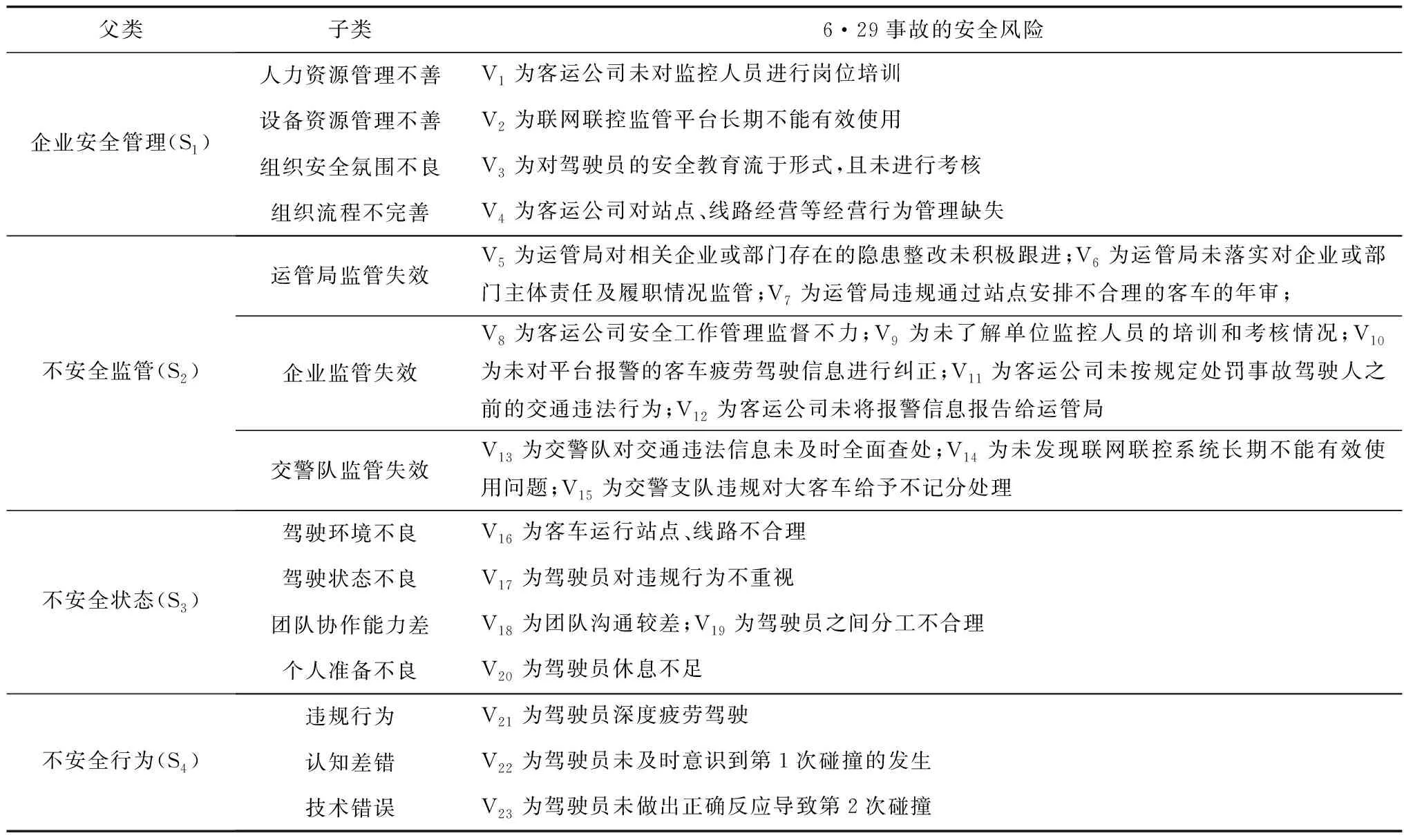
表1 “6·29”重大道路交通事故安全風險分類Table 1 Safety risk classification of “6·29” major road traffic

3.1.2 事故風險關聯分析

在確定網絡節點后，只需給相關節點之間加上連邊就形成了網絡。搜集近年120個交通事故案例，20個1組，整理成道路交通風險數據集，計算與“6·29”事故有關的兩兩風險之間的spearman系數，查閱秩相關系數檢驗的臨界值表顯示當系數大于0.415，則認為兩風險相關。各節點之間用有向線段表達風險之間的的因果關系確定鄰接矩陣A(表2)，構建網絡(圖2)，圖中最下方4個節點代表父類，四大類各自延伸與相應分類中的風險連接，但四大節點及其連邊主要用于體現節點間的關聯趨勢，并不參與計算。

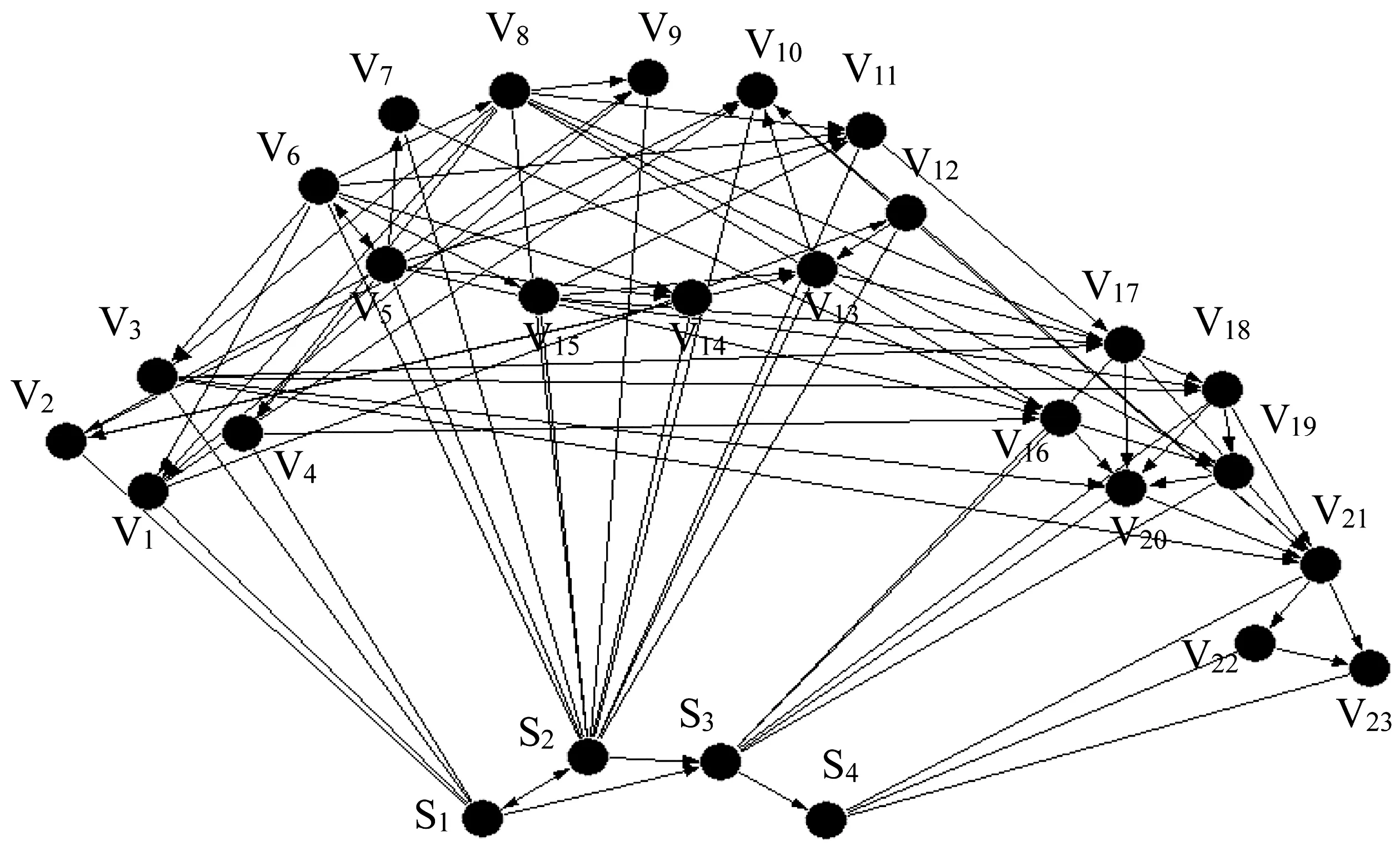
圖2 “6·29”道路交通事故安全風險網絡模型Fig. 2 Safety risk network model of “6·29” road traffic accident

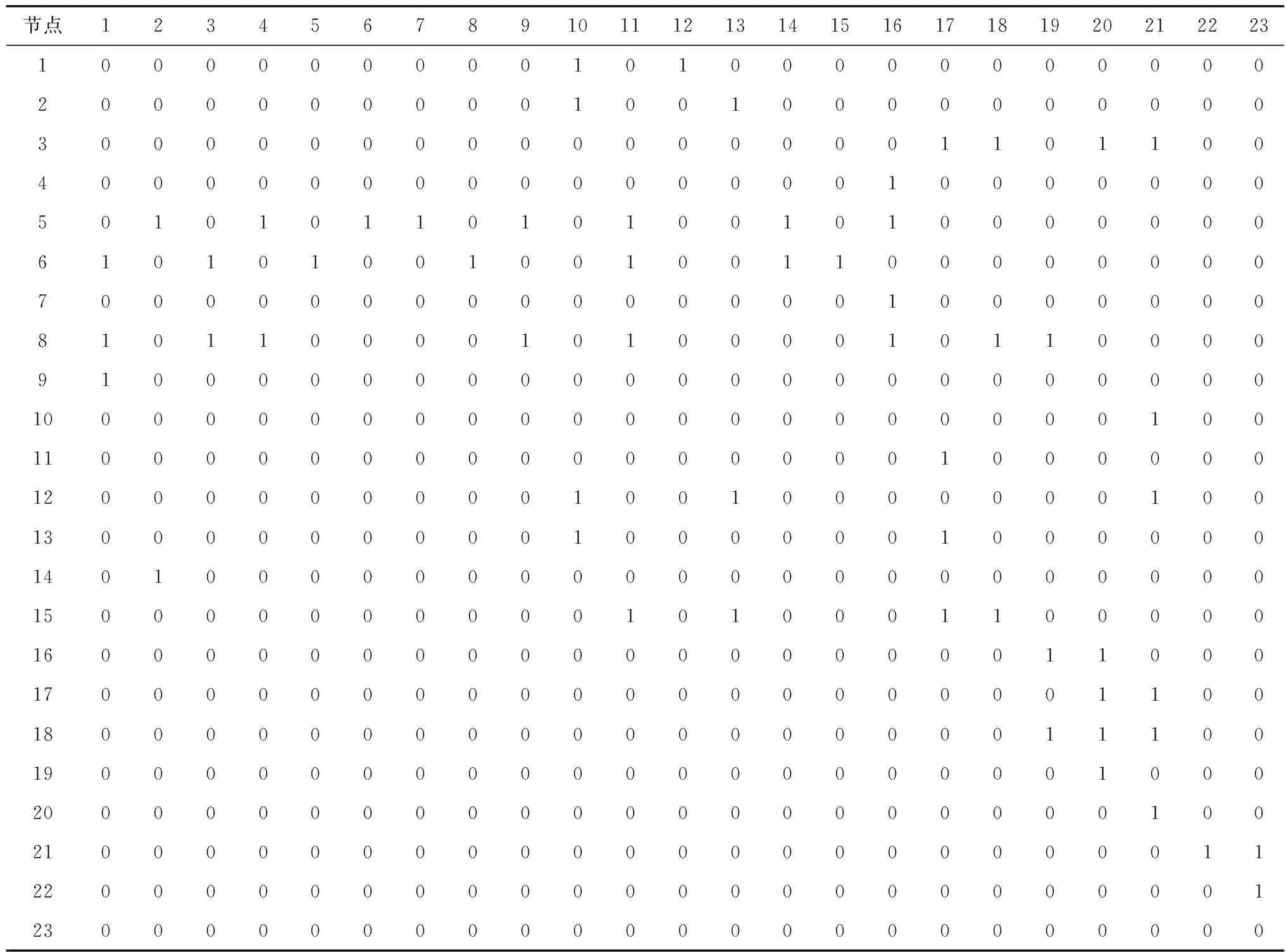
表2 “6·29”重大道路交通事故安全風險鄰接矩陣Table 2 Safety risk adjacency matrix for “6·29” major road traffic accident

3.2 網絡風險中心性分析

各事故影響因素點度中心性圖3(a)、接近中心性如圖3(b)、介數中心性如圖3(c)。由分析結果可知，V8和V5在本網絡中度中心性最大，若將這兩個風險嚴格控制可以很大程度上減少其他風險的發生和發展。V8和V6接近中心性最大，這說明兩個節點與其他風險的關系最為緊密。介數中心性體現的是節點在網絡中的媒介作用，駕駛員深度疲勞駕駛(V21)是該網絡中最大的媒介，控制該風險發生也就很大程度上控制風險的傳播。

圖3 度、接近、介數中心性分析結果Fig. 3 Analysis results of degree, closeness and betweenness centrality

3.3 網絡風險綜合排序

由于在該起事故中，客車第2次碰撞才最終導致巨大人員傷亡和財產損失，故取駕駛員未做出正確反應導致第2次碰撞(V23)為事故節點，3個指標經過PPR方法分析后得到的最終事故節點Pr值分別為：0.082 4、0.083 9、0.092 0。為使所構造權重矩陣滿足和為1，且不改變數據結構，對其進行百分化，得到指標權重矩陣為w=[0.319 0 0.324 8 0.356 2]，可見這3個指標中中介數中心性指標較另兩個指標更加關鍵。在已知指標權重的基礎上列出規范加權矩陣A，得到Z+=[0.319 1,0.324 8,0.356 2]和Z-=[0,0,0]，再根據式(8)和式(9)計算正負歐式距離S+、S-，最終得到各風險貼近度T見表3，以及根據貼近度得到的風險排序見圖4。

由貼近度定義可知，貼近度表示接近程度，也可表示關聯度，在交通風險分析中，可以表示各因素對事故的影響程度。由結果可知，疲勞駕駛對該起事故的發生影響最大，接近程度達到了89%；其次，運管局和企業的監督管理不力對該事故的發生影響較大，與事故接近程度達到了58%，駕駛員對違規行為的不重視、休息不足等與事故接近程度超過了50%。該事故實際調查結果顯示：事故直接原因是過度疲勞，間接原因是有關運輸企業安全生產主體責任不落實、有關監管部門履職不到位，另外駕駛員休息不足，且曾多次違規等都是間接導致事故的原因[13]。可見該方法得到的排序結果與實際事故調查結果大致符合。

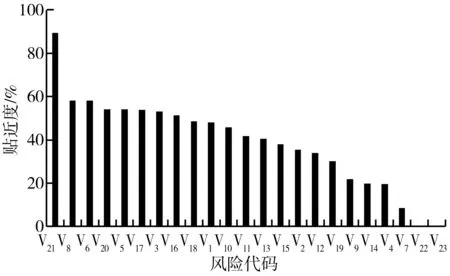
圖4 “6·29”交通事故風險影響度綜合排序Fig. 4 Comprehensive ranking of 6·29 traffic accident risk impactdegree

表3 各風險貼近度計算結果Table 3 Calculated results of each risk closeness degree

3.4 方法對照及討論

熵權法是一種客觀賦值方法，熵權TOPSIS方法在各個領域已經有了較為廣泛的應用。筆者運用熵權TOPSIS方法對“6·29”交通事故進行分析，該方法具體實現步驟參考文獻[14]，與PPR-TOPSIS方法結果對照如圖5。

由對照結果來看，兩種方法的趨勢部分一致，證明了PPR-TOPSIS方法的可行性和準確性。另外，由圖5容易發現熵權TOPSIS方法圖形趨勢與度中心性類似，將其與度中心性標準化結果d對照如圖6，發現其圖形趨勢與度中心性高度重合，說明熵權TOPSIS法受度中心性的影響極大，而PPR-TOPSIS法相對來說所受單個值影響小，較之綜合性更強，參考意義更大。

從排序結果來看，兩者風險排序略有不同，這是因為權重的計算方法有所差別，PPR方法是取迭代后各指標值對事故的影響值作為權重；熵權法取靜態過程的指標值計算信息熵后處理作為權重。PPR-TOPSIS方法分析結果顯示駕駛員深度疲勞駕駛(V21)是對事故影響最大的風險，其次是企業和運管局監管問題；而熵權TOPSIS分析結果顯示客運公司安全工作管理監督不力(V8)為最大風險，排名前三的風險都是監管風險。結合事故調查報告的實際情況，PPR-TOPSIS方法所得結果與調查結果相符，而熵權TOPSIS法與調查結果不太符合，因此，PPR-TOPSIS方法更能滿足道路交通風險分析要求。

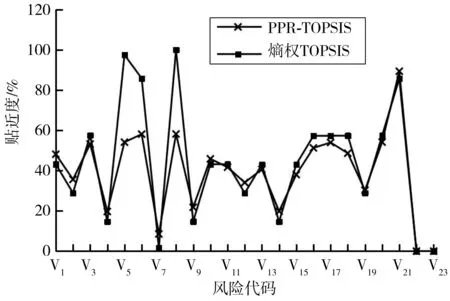
圖5 PPR-TOPSIS和熵權TOPSIS結果對比Fig. 5 Comparison of PPR-TOPSIS and entropy-TOPSIS results

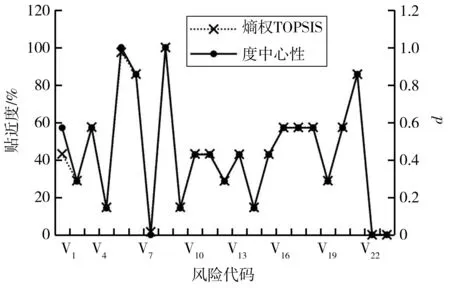
圖6 熵權TOPSIS結果和度中心性數據對比Fig. 6 Comparison of entropy-TOPSIS results and degreecentrality data

4 結 論

城市道路交通安全影響因素眾多，牽涉較廣，是一復雜系統工程，這些特征為復雜網絡模型的構建提供了基礎。

1)筆者對傳統TOPSIS方法進行了改進，以PPR方法為橋梁，使之與復雜網絡緊密結合，融合成PPR-TOPSIS客觀排序方法。并使HFACS模型、復雜網絡理論和PPR-TOPSIS綜合排序三者結合形成了一套完整的道路交通安全風險分析體系。

2)將PPR-TOPSIS與熵權TOPSIS方法相比較，發現對于道路交通風險的分析PPR-TOPSIS方法準確性，綜合性更高。

3)通過對典型事故的分析發現嚴格控制駕駛員的不安全行為能夠最大程度的控制事故，有效的上下監督能夠對道路交通安全起到很大的作用，為了減少這類事故的發生需要對駕駛員嚴格要求，完善駕駛員技術、安全培訓體系；同時嚴格要求監督組織或成員將責任落實到位。