基于多目標規劃指標體系的原料訂購運輸模型研究
許晗 張睿思 張靜涵 李東格 徐涵玫
(曲阜師范大學經濟學院 山東日照 276827)
生產制造企業原材料的訂購與運輸指從材料的采購開始,滿足最終客戶的所有流程,是由供應商、轉運商、倉庫組成的物流網絡。供應鏈成員之間的在制品庫存和最終產品代表了供應鏈中的貨物流[1]。在實踐中,企業通常依據材料價格、訂單交付能力等指標選取供求關系穩定的優質供應商,依據最大轉運量、材料損耗程度遴選運輸性能良好的轉運商,從而制定有效降低企業成本、保障企業生產、提高企業產能的訂購與轉運方案,對增強競爭力優勢、實現利益互補、合作共贏具有重要的戰略意義。
1 數據預處理
1.1 供貨特征指標體系
(1) 供應商交付能力。供應商的交付能力是決定企業供貨能力的重要因素。交付能力指交貨及時性和交貨周期,此題中用交付率進行衡量,交付率越高的供應商,供貨能力越強。交付率Ri為供貨量在訂購量中的占比,具體公式如下:
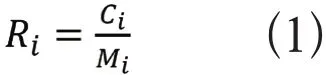
其中Ri是交付率,Ci是供貨量,Mi是訂購量。
(2)供應商供求關系穩定性。指供應商實際提供原材料數量與企業訂單所訂購原材料數量兩者關系之間的穩定程度。
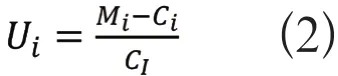
其中,Ui是交付差額比。
1.2 數據可視化處理
借助Lingo軟件,可根據供應商提供的材料類型、企業訂貨量、供應商的供貨量、生產周數實現對數據進行總體與局部的可視化處理(以A為例),如圖1所示。
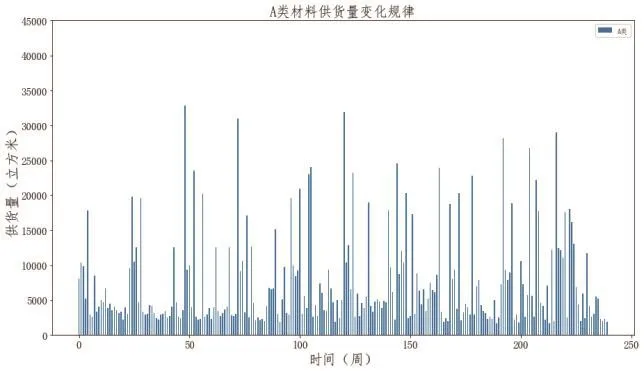
圖1 A材料供應商的供貨量隨時間分布情況
通過對比A、B、C不同類型材料供貨量在240周內隨時間變化的規律可以發現,提供A材料供應商的供貨量隨時間變化波動幅度較大,B材料供應商次之,C材料最小,且峰值出現在C材料供應商中。經過統計對比發現,在原材料特殊性的約束下,供應商通常不能保證嚴格按訂貨量供貨,傾向于選擇實際供貨量少于訂貨量。
2 灰色關聯分析模型建立
規定供應量數據[2]作為參考數列:
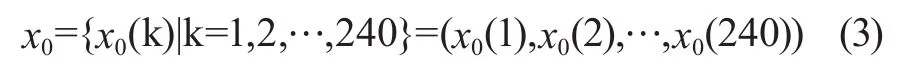
其中,k表示周數。
規定交付率與交付差額比數據為比較數列:
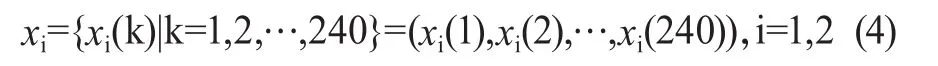
采用均值化對數據進行無量綱化處理:
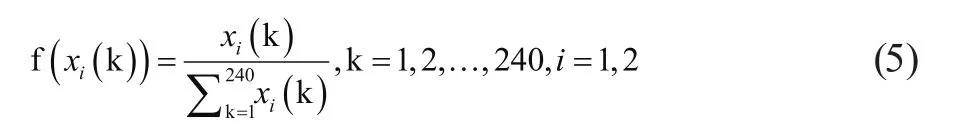
先計算差異序列。將無量綱化處理后的參考序列各期的數值與比較序列對應期數值的差值的絕對值記為?0i(k)=|xi(k)-x0(k)|,i=1,2;k=1,2,…,240。則{?01(k),?02(k),…,?0w(k)}組成2×240維的差異矩陣。一般情況下,?0i(k)越小,表示兩個指標數據相近程度越大,關聯性越好。再計算最大極差與最小極差。?max=maximaxk|x0(k)-xi(k)|為最大極差,是所有比較數列與參考數列的絕對差值中的最大值;?min=minimink|x0(k)-xi(k)|為最小極差,是所有比較數列與參考數列的絕對差值中的最小值[3,4]。
參考序列x0(k)與比較序列xi(k)在時刻k時的關聯系數計算公式為:
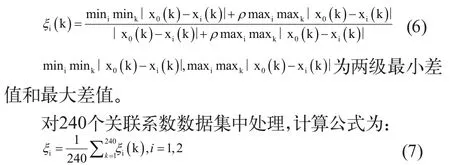
3 灰色關聯分析模型求解
3.1 關聯系數計算求解
先提取402個供應商240周的供貨量、交付率、交付差額比數據建立原始數據表。而后將供貨量、交付率、交付差額比三列數據分別除以每列均值對數據進行無量綱化處理,而后計算關聯系數[5],如表1所示。

表1 計算關聯系數
根據灰色系統理論,運用灰色關聯系數[6~8]計算交付率、交付差額比與供貨量之間的灰色關聯度。同時,經過灰色關聯分析模型,可以求出供應商指標數據的402對灰色關聯度,關聯信息分散,不利于確定總體指標權重,可將每個指標402個關聯度取平均定義單個指標總體灰色關聯度。由關聯度結果可知,交付率與供貨量的灰色關聯度要大于交付差額比與供貨量的灰色關聯度,表明交付率對供貨量的影響程度更大。基于此,規定交付率指標權重為0.6,交付差額比指標權重為0.4。
3.2 單個供應商在兩項指標上的總得分計算
由于每個供應商對應240周的指標數據,一般情況下,距離當前時間點最近的時間發生的行為與當前時間即將要發生的行為相似度最高,假設W001的時間距離當前時間點最遠,而W240的時間距離當前時間點最近,據此,從W240到W001依次均勻遞減對指標數據賦權,即從權數1~0依次以間距0.0041遞減。再將240個指標數據的權值與對應指標數據相乘求和,即
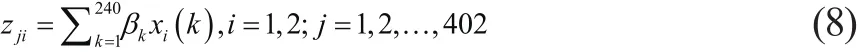
zji為第j個供應商在第i個指標上的綜合指標值。將單個供應商賦權后的綜合指標數據與規定評分表對應,得出單個供應商在單個指標上的綜合得分,如表2所示。

表2 指標評分表
由此將單個供應商的兩個指標綜合得分加總,再對402家供應商的總得分進行排序,得到評分最高即保障企業生產最重要的51家供應商,排名如表3所示(以前十名為例)。
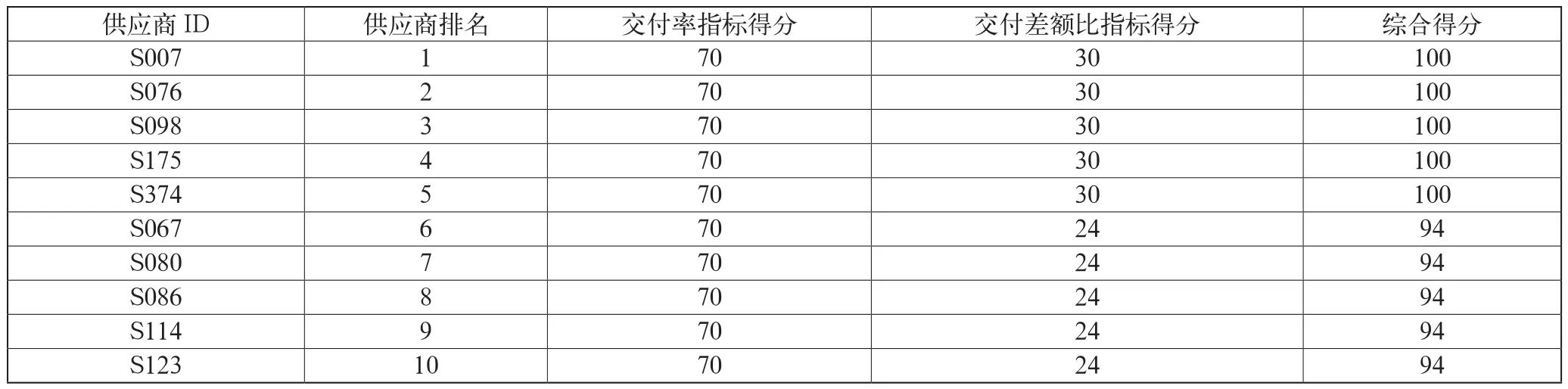
表3 保障企業生產最重要的50家供應商
4 遺傳算法下的單個材料供應商選擇多目標規劃模型
4.1 決策變量
本文設定企業每周能夠滿足產能生產2.82萬立方米,需要最少選擇提供A的供應商a個,提供B的供應商b個,提供C的供應商c個,需要消耗A類原材料生產x單位產品,或B類原材料生產y單位產品,或C類原材料生產z單位產品(單位:立方米)。Zi是企業原材料的接受量(企業實際生產產品所需要的材料數量),i表示從i個供應商之間進行選擇(i=1,2…402)。
4.2 目標函數與約束條件


約束條件4:運輸損耗率rij介于0~1,且僅由接受量和供貨量決定。

4.3 計算結果
使用MATLAB軟件對該模型進行求解,可得a=0,b=17,c=24,若要滿足企業生產的需求,至少應選擇17家生產B材料的供應商,24家生產C材料的供應商來供應原材料。故結合第一問的灰色關聯分析模型的打分結果篩選出以下供應商,如表4所示。
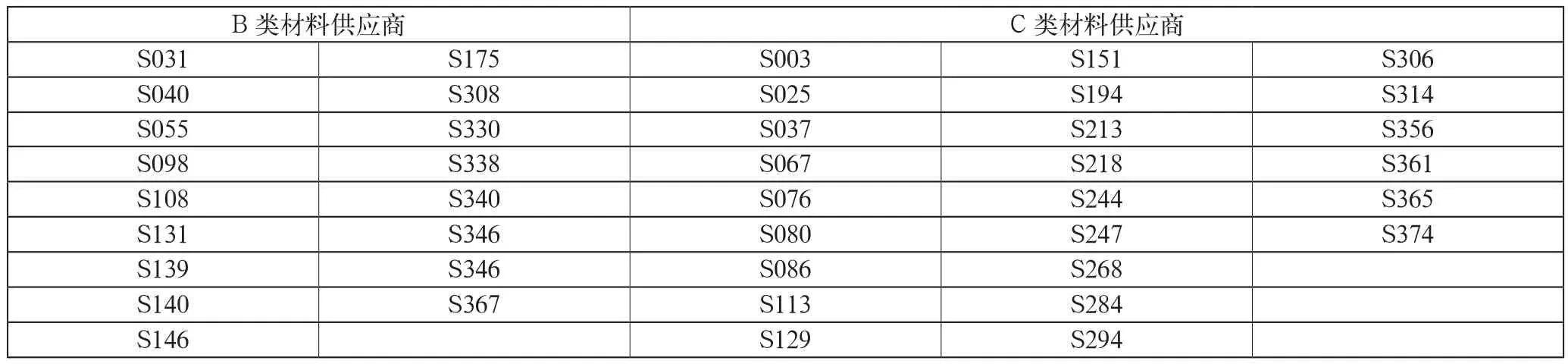
表4 篩選出B類TOP17和C類TOP23供應商
5 多供應商配送期量標準雙層規劃模型
根據企業每周生產計劃需求,確定各供應商的訂單需求量及供貨能力,考慮到供應商采購成本、運輸儲存成本和轉運商的運輸損耗率約束,從而建立多供應商配送期量的雙層規劃模型,設計出滿足公司經濟效益最好,損耗最少的訂購運輸方案。
多供應商配送批量優化模型。以訂購及運輸過程中的總成本TC最小化為目標構建函數關系,同時考慮不同供應商的交付能力與服務水平,建立供應商配送批量優化模型,預計公司針對滿足生產需求供應商在未來24周內每周訂貨量及頻次。當訂購量不足最優配送量時,為滿足生產需求往往按供貨量進行轉運,因此供應商每周材料轉運總量不低于生產需求量。
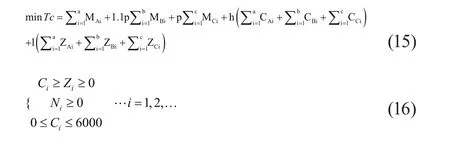
總成本最低的目標函數主要由公司向供應商采購成本、轉運商轉運成本和倉庫儲存成本三部分構成。約束條件要求保證單次供貨量不能超過轉運商最大運輸量。此外,還需保證供應商單次供貨量滿足總需求與訂購運輸周期內的物料消耗。

基于遺傳算法進行求解,可以得出企業未來24周針對41家供應商每周最經濟的原材料訂購方案。
6 結語
圍繞原料訂購與運輸過程,本文提出基于供貨特征可視化與灰色關聯分析法相結合的供應商選擇模型。首先,以“訂貨量”和“供貨量”構造“交付率”和“交付差額比”的指標體系;其次,根據“交付率”“交付差額比”“交貨及時性”“供貨量”四個特征,構建一個基于灰色關聯分析的供應商決策模型可對供應商進行篩選;最后,基于遺傳算法構建多目標規劃模型,求解供應商數量最小值判定的問題,為原料的訂購與運輸過程提供模型依據與參考。
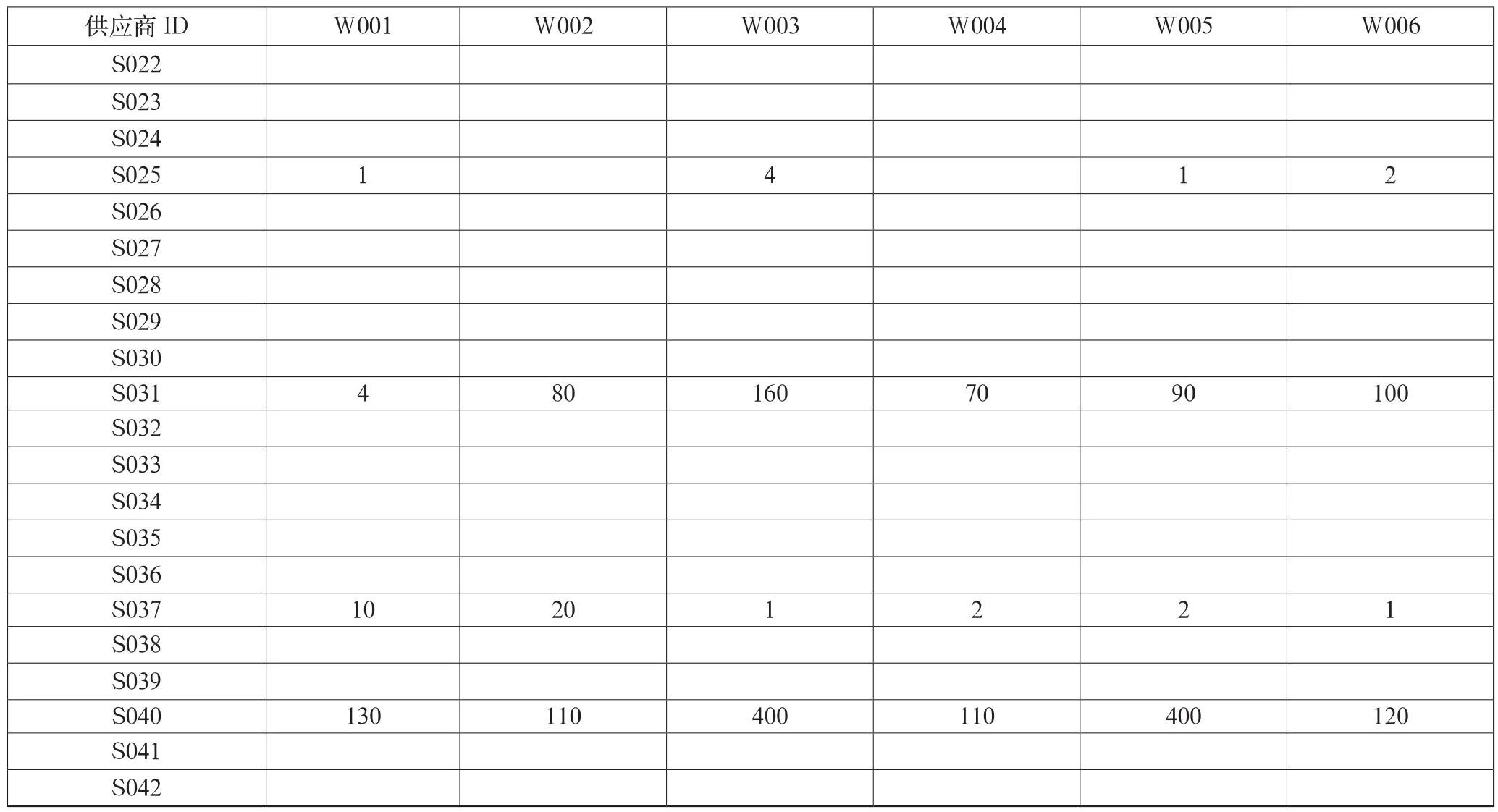
表5 企業未來24周每周最經濟的原材料訂購方案

