面向小樣本數據的水下目標識別神經網絡深層化研究

吳晏辰, 王英民

(西北工業大學 航海學院, 陜西 西安 710072)

水下目標識別作為水聲工程的重要技術領域,一直是海洋軍事和民用的主要研究方向之一。隨著近年來水下軍事目標小型化、消聲化,民用目標復雜化、精確化的趨勢不斷加深,對于水下目標識別系統的精度和靈敏度都產生了更高的要求[1]。

與傳統的利用基于先驗知識的人工聽音和譜圖等信息進行目標識別不同,利用基于深度學習的水下目標識別系統,可以滿足現代海洋作戰、作業對于目標自動識別、快速識別的迫切需求[2]。能夠實現這一需求的主要原因在于深度學習提取目標聲學信號中的各類特征作為基礎,利用信號處理的方法,將多種信號特征通過近年來蓬勃發展的各類人工智能分類器,以實現自動識別的目的。現有研究表明,目前利用各種方法所提取的信號特征在用于水下目標識別時,在實驗室驗證的效果普遍較好,但在實際水下噪聲環境中,應用性能卻出現了明顯下降[3]。出現這種現象的主要原因在于:一是相較于實驗環境,實際水下環境復雜許多,相應的樣本數量與基于大數據的深度學習網絡所需的量較少;二是在復雜聲環境下的信號信噪比不佳,存在多目標或強干擾的情況下,容易導致特征提取出現誤差偏離;三是對于目標聲信號本質的特征提取方法的研究還不夠。

為了研究產生應用性差異的原因,本文選擇了2種具有相關性且有較為明顯差異的特征提取方法。作為目標應用最廣泛的水聲特征提取方法,梅爾倒譜系數特征提取方法(Mel-frequency cepstral coefficients,MFCC)可以將聲音信號的實際頻譜轉化到感知頻域中進行研究,從而有利于系統模擬人的感知過程,在性能和穩健性方面比較符合實際的聽覺效果[4]。而在MFCC基礎上改進的Gammatone頻率倒譜系數法(Gammatone frequency cepstrum coefficient,GFCC)在保有MFCC優點的同時,在水下復雜聲場環境中, GFCC較MFCC具有更優良的抗噪能力[5]。

2006年Hinton提出了以卷積神經網絡(convolutional neural network,CNN)為主體的深度學習模型[6]。CNN具有自適應尋找最適合分類器的能力,CNN由于采樣層的存在,具有時移不變性的特征[7]。與傳統識別方法相比,CNN通過尋找使識別效果最優的參數,使網絡可以擺脫人工經驗的影響,對復雜的應用條件具有更好的適應能力。而基于CNN卷積核改進的殘差神經網絡(ResNet),充分利用了神經網絡的函數擬合特性,對于水下目標的輻射信號而言,基于CNN的深度殘差網絡可以一定程度上獲取常規特征分析方法難以發現的隱含關聯,即作為特征提取器的同時,亦可作為分類器,因此非常適合處理原始水聲信號。

本文給出了一個面對水下目標識別小樣本數據的基于卷積神經網絡的深層神經網絡構成方法。利用MFCC和基于MFCC改進的GFCC作為特征提取方法,構建卷積神經網絡與殘差神經網絡形成比對網絡,建立了小樣本下的水下目標識別系統,并對樣本在2種網絡的較深層結構下所取得的實際識別率與網絡預測值進行統計比對。發現由于特征提取方法與深度學習網絡的各種組合模式對于水聲信號諸如信噪比等特性的匹配程度不同,其表現出的實際識別率和網絡預測值有較為明顯的關系,抗噪較好的組合模式的梯度衰減、網絡識別穩定性和實際識別率較抗噪較差的組合具有更佳的網絡穩定性和準確率,根據這一依據,為復雜神經網絡神經元的設計提供了一種思路。

1 艦船輻射噪聲的特征提取

1.1 MFCC特征提取法

作為一種常見的聲音識別特征,MFCC特征提取方法主要分以下幾步:

1) 分幀

2) 求能量譜

為了得到信號能量譜,需要利用快速傅里葉變換對幀信號進行處理,其公式為

p(f)=|X(f)2|=|FFT(x(n))|2

(1)

式中,x(n)為輸入信號。

3) 濾波

將p(f)通過梅爾濾波器組,其公式為

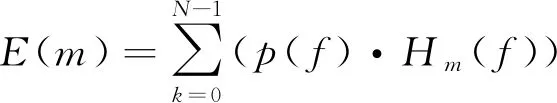
(2)

式中:N為幀數；Hm(f)為梅爾濾波器組系數。

4) 對數運算

對(2)式中E(m)求導,得到E′(m)

5) 求倒譜

對E′(m)求離散余弦變換,可得MFCC參數C(n),其公式為

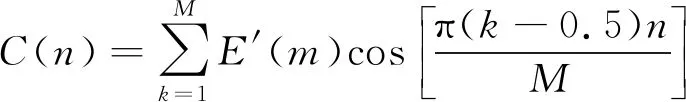
(3)

式中:n=1,2,…,p,p為MFCC的階數；M為濾波器的個數。

則MFCC特征參數的一階以及二階差分系數由(3)式可得,其公式分別為

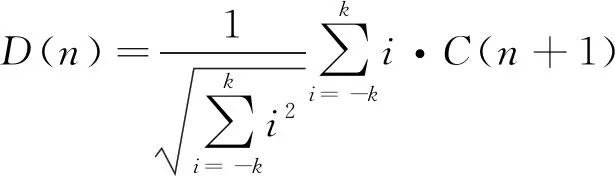
(4)

(5)

(3)～(5)式共同構成幀特征向量

Tn={C(n),D(n),D′(n)}

(6)

(6)式即為樣本信號的MFCC。

為了使系統的性能以及穩健性都相對符合人聽覺感知效果,利用MFCC特征參數分析方法將聲音信號頻譜轉換到模擬聽覺感知過程的感知頻域。圖1為梅爾頻率和線性頻率關系圖,通過關系圖可以得出以下分析:當頻率在1 000 Hz以上時,Mel頻率的分布趨勢為對數增長;而頻率在1 000 Hz以下時,Mel頻率的分布趨勢為帶寬100 Hz左右的線性分布[8]。

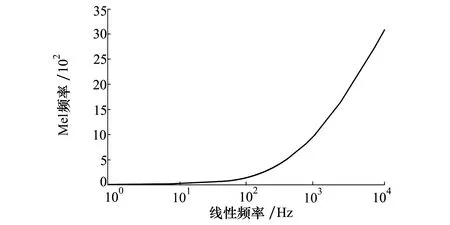
圖1 梅爾頻率與線性頻率的關系

利用倒譜變換進行各個濾波器組輸出的幅度與能量之間的強相關性解耦,常見的處理濾波器組輸出方法有對數壓縮以及余弦變換,得到的Mel倒譜系數的方程如(7)式所示

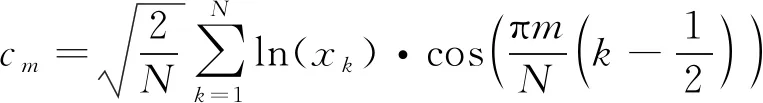
(7)

式中:N為濾波器的個數;m為倒譜系數的維數。

1.2 GFCC提取方法

圖2為GFCC特征提取的主要流程。

圖2 GFCC特征提取流程

具體如下:

1) 分幀。

2) 求能量譜。

對輸入信號x(n)使用離散傅里葉變換(discrete Fourier transform,DFT),其公式為

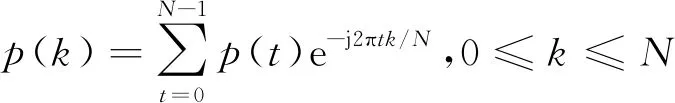
(8)

式中,N為DFT點數。

3) 濾波

鑒于Gammatone濾波器組無限長單位脈沖的特殊響應特性,Gammatone的濾波系數gi(k)可表示為

gi(k)=kn-1exp(-2πBik)cos(2πfi+φi)u(k)

(9)

式中:n為濾波器的階數;fi為中心頻率;Bi為濾波器的衰減因子;φi為濾波器的相位;u(k)為階躍函數。

將人耳聽覺特征臨界值作為各個濾波器的帶寬從水聲信號中提取特征時,可表示為

GEB(fi)=24.7×(4.37fi/1 000+1)

(10)

bi=1.019GEB(fi)

(11)

式中:bi是各個Gammatone濾波器的帶寬。

4) 對數運算

樣本信號的Gammatone能量譜EG(i)可通過將(8)～(9)式聯立取對數的方法獲得,表示為

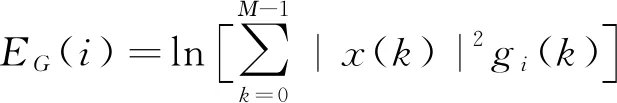
(12)

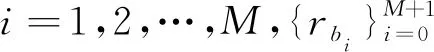
5) 求倒譜

利用離散余弦變換,得到Gammatone系數,其可表示為

0≤n≤Μ-1

(13)

GFCC的計算方法為:求(13)式最大值、平均值、最小值、標準差以及中值等5種統計參數。

2 神經網絡構造

2.1 卷積神經網絡

CNN的主要思想來自局部連接和權值共享,通過卷積操作實現局部連接,這個局部區域的大小就是濾波器filter。為實現多層網絡,需要盡量避免全連接過程中參數繁雜進而造成無法完成計算的問題,同時還可以借助參數共享的方法減少實際運算參數的數量[9]。通常一個普通CNN包括輸入層、池化層、激活層、全連接層和輸出層等。由于輸入層和輸出層的外部通常處于不可見狀態,故稱為隱含層。

2.2 殘差神經網絡

在確定水下聲目標的特征提取方式時,抽取了與目標有關的有效信息，同時也會舍棄許多原始信息,這使得本就難以獲取的樣本信息沒有充分利用。同時這些特征往往受到信道、環境等多種因素的影響,難以保證高度的穩定性[10]。為了保證網絡穩定性和原始信息特征的充分利用,往往需要將淺層深度學習網絡向深層發展。雖然理論上,假如深層網絡B是淺層網絡A的恒等映射,那么B至少應當與A性能相同,然而在實際實驗中,隨著網絡的不斷加深,網絡梯度的不斷消失最終會導致深層網絡出現退化現象:網絡隨著深度的增加,在識別率達到飽和后迅速退化[11]。為了解決這個問題,ResNet團隊給出了通過設計殘差單元的方式有效降低退化現象對系統的影響,其主要思路是通過構建“快捷連接(shortcut connection)”的構建塊,將輸入信號與經過卷積處理的輸出信號恒等映射,從而組成一個殘差神經元,其構成的殘差網絡主要結構見圖3。

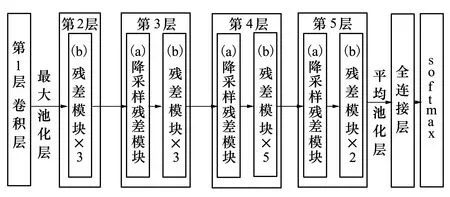
圖3 殘差神經網絡結構

3 改進的殘差神經網絡結構設計

基于Inception模塊改進的數據池化層是由GoogLetNet在神經框架中首次采用的優化模塊,后經過幾次版本的迭代,一直到最新的Inception-v4和Inception-resnet,每個版本在性能上都有一定的提升。通過建立小卷積層的串聯化,當系統輸出來到大卷積層時,基于堆疊替換的方法,拼接多種特征維度層面,來達到提升神經網絡學習效率的目的。由于傳統殘差神經網絡的目標是實現百萬級以上的大訓練樣本及多GPU運行的復雜訓練,在數據輸入時,會將輸入到池化層的數據通過7×7的大型卷積層和池化層。在面對具有時變性強的如輻射噪聲等類型的時域信號時,如果有效樣本有限,則很難利用大卷積層完成數據堆疊,無法有效提升網絡的學習效率。因此本文針對基于Inception的模塊特點設計了一種改進的數據池化層,這種池化層在面對小樣本數據時具有較強的特征提取能力。

為了改進數據池化層,將傳統的7×7的卷積層替代為3個3×3的小卷積層,并將每個通道數分別設置為8,16,16。為了有效提升神經網絡的特征提取速度,在每個3×3的小卷積層后面都加入了批量標準化和ReLU激活函數。傳統加入單一ReLU激活函數的方式,會隨著網絡層數加深出現過擬合的問題,為了解決這個問題,給每個小卷積層都加入了一個ReLU激活函數,使網絡對小樣本特征信息的提取能力更強,之后再在Concat層將特征維度拼接到一起。為了避免小樣本下網絡層數加深可能導致訓練過程中過早出現過擬合問題,將改進的殘差連接結構加入到數據池化層中,再從最大池化層的輸出中提取得到數據特征信息。

4 系統實驗分類結果和分析

在本研究中,實地采集艦船輻射噪聲樣本數據1 756份,取自互聯網的海洋生物噪聲樣本數據877份,利用高斯模擬或水下實測的其他水下噪聲樣本6 410份。每個樣本都被裁剪為大小40幀,幀移15 ms的塊,由這些塊所組成的數據集統稱為樣本集(epoch),當樣本集過大或根據研究需要時,可以將樣本集按照一定數量進行分批(batch),每批大小(batch size)固定。在對樣本集做過批處理后,將這些樣本分別采用經過改進后的GFCC特征和MFCC特征進行訓練, 并使用深層殘差神經網絡進行目標分類。

在得到匹配本研究的神經元組成結構后,將MFCC和GFCC與殘差網絡組成的神經元分別進行全樣本訓練,在多次訓練后,對輸出求取均值后得到神經網絡分類結果,見表1～2。

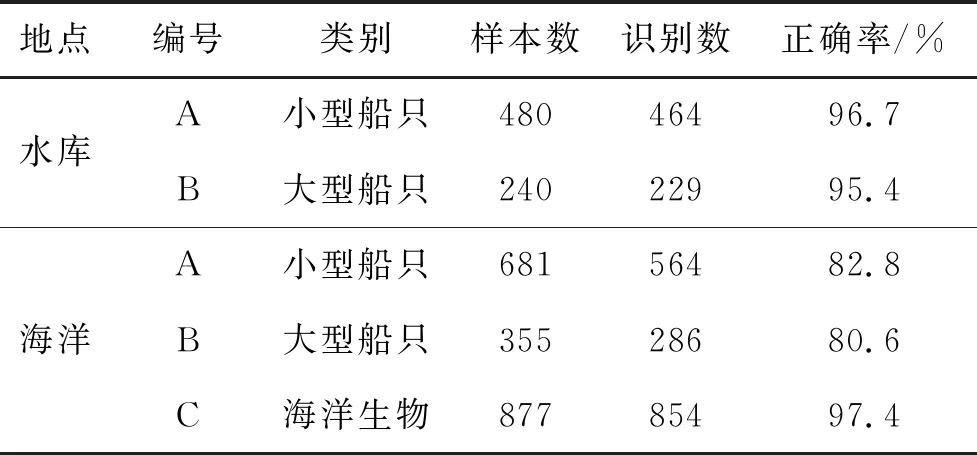
表1 Mel頻率倒譜系數特征提取后樣本識別統計結果

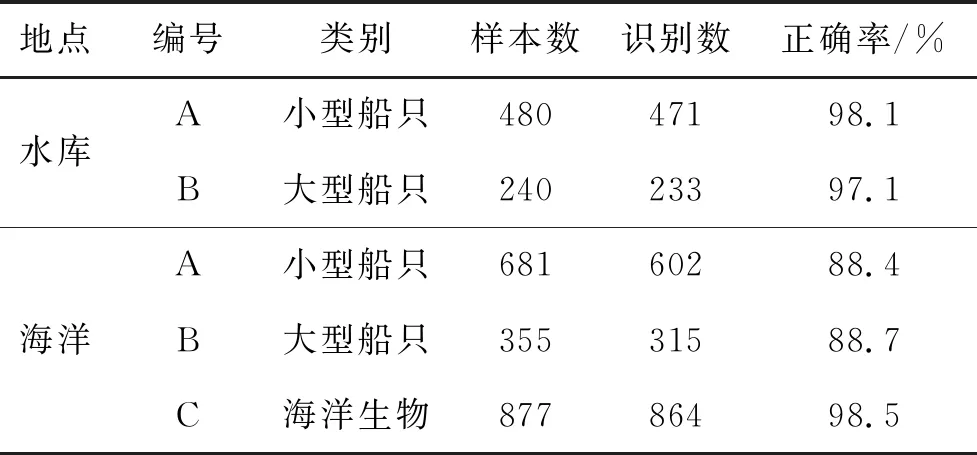
表2 CFCC特征提取后樣本識別統計結果

在對分類結果做分析時,由于檢測點較多,所以僅展示前10個檢測點在前10層網絡下的網絡預測率和實際識別率。需要說明的是由于動物叫聲具有比較顯著的聲學特征表現[12],考慮到對比的特征較多,工作量較大,所以在樣本集中加入了動物叫聲作為目標樣本,以在合理范圍內降低運算參數,增加研究效率。

利用MFCC作為特征提取方法應用在CNN網絡中的神經元網絡測試結果,如圖4所示。圖中網絡深度表示神經網絡的層數,在實驗時將特征提取在深度達到每一層時的預測結果標記在圖上形成曲線。根據結果可以發現,在網絡深度達到5層時,10個預測點的網絡預測值趨近于100%,再將被網絡貼上標簽的識別樣本與實際樣本集進行對比,得到實際正確率,如圖5所示。實驗結果表明實際識別率在網絡達到6層時出現了明顯衰減,且在整個檢測過程中實際正確率一直與網絡預測值存在著一定的差值,其差值在6層時出現最小值,約為25%左右。

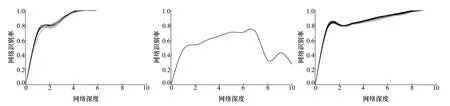
圖4 基于Mel頻率倒譜系數特征提取的卷積神經網絡預測值 圖5 基于Mel頻率倒譜系數特征提取的卷積神經網絡實際識別率 圖6 基于Gammatone頻率倒譜系數特征提取的卷積神經網絡預測值

將基于MFCC改進的GFCC特征提取法應用于CNN網絡中,其網絡預測值和實際識別率如圖6和7所示,可以發現在網絡深度達到8層時,網絡預測值趨近于100%,與實際識別率相對比,其差值為10%左右,其實際識別率在深度達到9層時出現了明顯衰減。

通過研究,對產生這種現象的原因做了如下幾點推測,首先,神經網絡由于其計算方式不是線性的,在小樣本情況下,每一次樣本輸入進入卷積核后,通過反復卷積-池化-反向傳播的計算會產生多個帶有不同標簽的結果,只有在樣本大小匹配網絡結構的情況下,網絡對權重的選擇才會逐漸趨向固定,輸出值才會趨向于唯一。另外由于梯度彌散問題,當神經網絡深度達到一定值時,梯度衰減過快會導致卷積層內的部分卷積核出現無效化從而出現“卷積核死亡”的問題,可能正是因為這種線性導致了在某層出現的識別率快速衰減的結果。

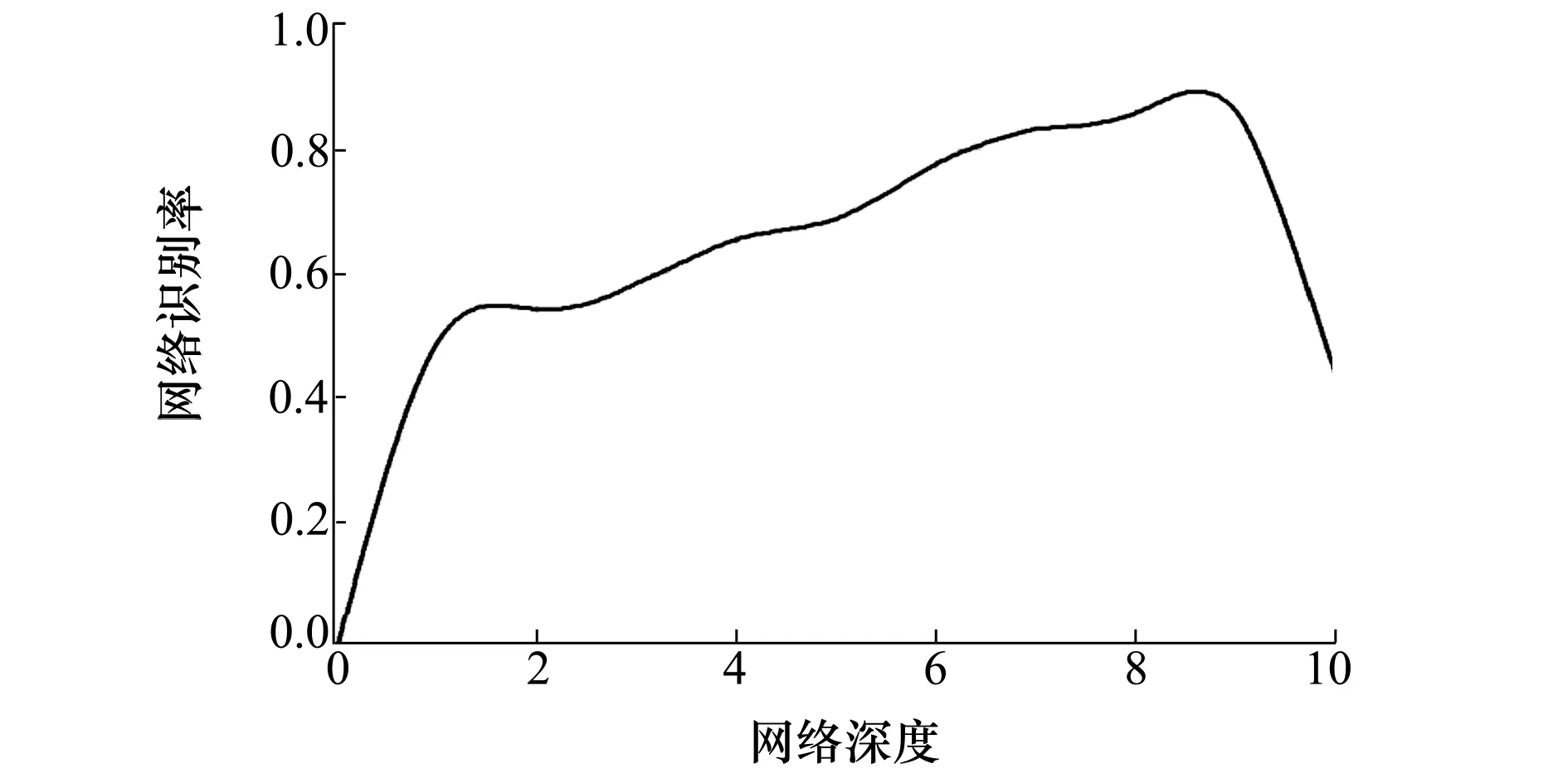
圖7 基于Gammatone頻率倒譜系數特征提取的卷積神經網絡實際識別率

因此,在研究對象為小樣本的客觀基礎上,很容易得到一種直觀判斷神經元構成的標準,也就是利用輸出結果平穩性、神經元死亡深度來判斷特征提取法和網絡關于本研究的匹配程度,從而決定最終神經元的組成結構。

在文獻[11]中發現2015年研發成功的殘差神經網絡(ResNet)具有比較好的抗噪抗彌散性能,且常被用于(相對)小樣本問題的處理上,因此嘗試了幾種特征提取與殘差神經網絡的融合,同CNN網絡一樣,本文將其前10個檢測點的10層網絡識別數據分別展現如下。

首先是將MFCC與ResNet進行融合,其網絡預測值和實際識別率如圖8和圖9所示,由預測結果圖可以看出,當網絡深度為7層時,ResNet網絡預測值趨近100%,而與實際識別率相對比,其差值最小為20%左右,實際識別率在深度達到7層時出現了明顯的衰減。

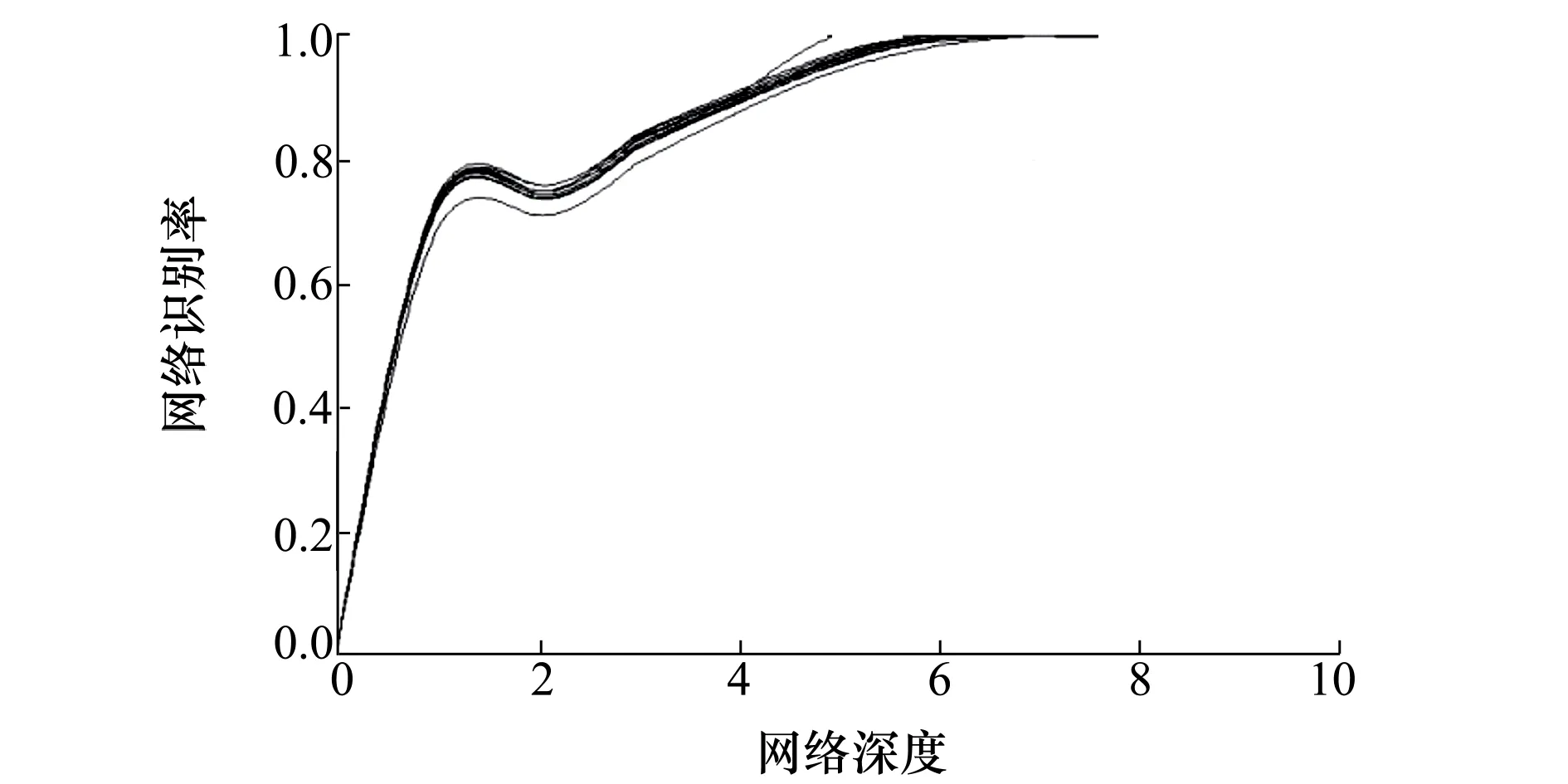
圖8 基于梅爾頻率倒譜系數特征提取的殘差網絡預測值

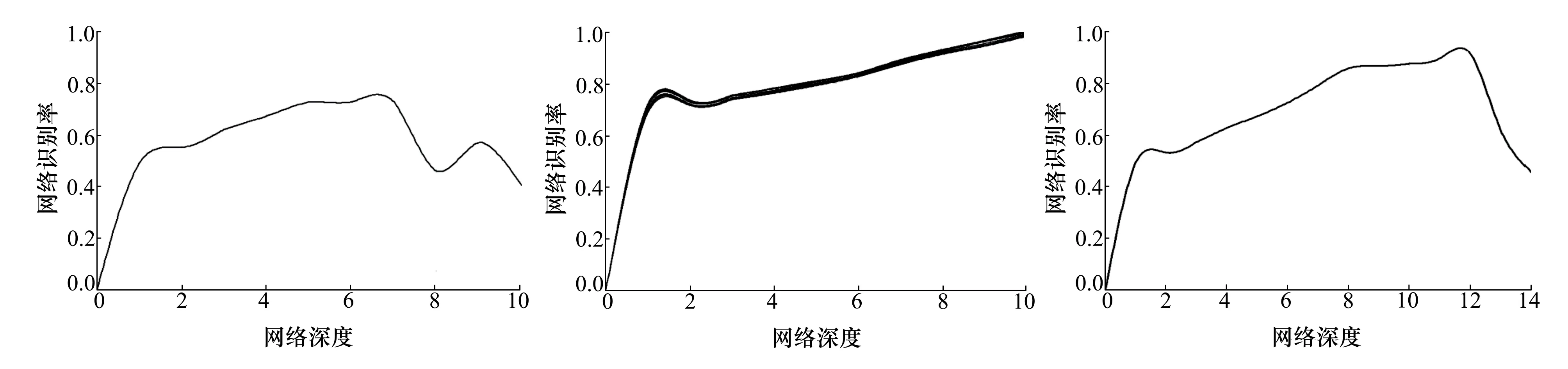
圖9 基于Mel頻率倒譜系數特征提取的殘差網絡實際識別率 圖10 基于Gammatone頻率倒譜系數特征提取的網絡預測值 圖11 基于Gammatone頻率倒譜系數特征提取的實際識別率

將GFCC與ResNet融合,其網絡預測值和實際識別率如圖10和圖11所示,由預測結果圖可以看出,該網絡在深度為10時雖然接近100%,但仍未到飽和程度,而與實際識別率相對比,其差值為10%左右,為了研究該網絡的衰減層數,將該網絡的深度加深到15層,可以明顯看出,基于GFCC的殘差網絡在12層時出現了衰減,其實際識別率差值小于10%。

5 結 論

通過研究發現，面向水下目標識別的深度神經網絡,其識別穩定性與識別準確率與目標特征提取方法、所選用神經網絡模型之間有密切的聯系。與常見的淺層水下目標識別神經網絡系統相比,利用如改良的殘差神經網絡等具有較強抗網絡退化功能的網絡結構,同時選擇匹配的特征提取法所組成的網絡,可以有效增加網絡的深度,提高小樣本利用率,增強系統對于多種目標在水下復雜環境中的識別效率。在使用GFCC作為特征提取方法的殘差神經網絡中,深層網絡的識別率和系統穩定性都顯著強于使用其他多種組合。這說明,對于基于小樣本的水下目標識別系統,在選擇特征提取方法和神經網絡模型時,應當擇優考慮抗噪強,梯度衰減弱,具有強抗退化的種類,以達到網絡深層化,以及充分利用有限樣本內的各類目標信息的目的。