一種基于自適應抗差CKF算法的改進初始對準方法
李璞, 楊濤, 牟宏偉
(1.國防科技大學, 湖南 長沙 410073; 2.中國運載火箭技術研究院, 北京 100076)
捷聯慣性導航系統(strapdown inertial navigation system,SINS)的核心是依托內部慣性器件開展持續數據采集和累計,通過積分方法進行導航結果計算,且系統的初始值對于導航最終結果的影響非常大。在開始工作之前,SINS需要利用初始對準來確定載體平臺的起始姿態,且起始姿態的測量精度對于最終的定位精度具有重大影響。對于載體平臺是靜基座的情況,假定系統失準角較小,系統誤差模型符合線性特性,SINS一般采取卡爾曼濾波器(Kalman filter,KF)來進行初始對準。然而,在某些惡劣或復雜工作場景下,基于粗對準后的平臺姿態誤差存在不滿足小失準角假設的可能,在這種情況下線性精對準方法往往無法獲取較高精度的對準結果,進而直接影響最終的導航精度。面對上述情況,諸多學者對基于非線性濾波算法和誤差模型的方法進行了研究。例如,劉海鵬介紹了擴展卡爾曼濾波器(extended Kalman filter,EKF)和無跡卡爾曼濾波器(unscented Kalman filter,UKF)在初始對準方位失準角大角度問題中的解決方法,并設計了相應的仿真評估測試。基于測試結果,可以發現UKF比EKF更適應大失準角度的情況;龍瑞則介紹了中心差分卡爾曼濾波器(central difference Kalman filter,CDKF)在初始對準方位失準角大角度問題中的解決方法,并基于仿真測試結果驗證了該方法的高效性;Jamshaid針對航向大失準角初始對準問題,也提出了比EKF 和 UKF 精度更高的二階分離插值濾波器(second-order divided difference filter,DDF2)[1-4]。
然而,上述傳統的非線性濾波器卻具有一定的缺點,如EKF由于復雜的導數,很難解析雅可比矩陣,且對于高度非線性化的系統,濾波效果并不好;UKF存在算法精度不高、穩定性差、對動態適應性低等缺點[5-7]。針對上述方法缺點,基于Spherical-Radial Cubature準則的容積卡爾曼濾波(CKF)在近段時間被廣泛應用,它可以適應非線性誤差模型,相比于傳統非線性濾波算法有所改進。
此外,如果衛星信號不穩定,觀測量也會存在粗差,進而影響濾波算法的估計效果。同時,多數情況下無法得到準確的干擾特性,使得濾波估計性能受到了很大限制。針對上述問題,本文基于自適應抗差理論設計了一種改進CKF算法。具體而言,通過穩健M估計和改進Sage-Husa次優無偏極大后驗估值器,使改進CKF算法具有更強的濾波穩定性和更好的自適應性。
1 SINS大方位失準角誤差模型
(1)
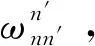
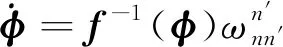
(2)
式中
根據文獻[1],可得SINS姿態誤差方程為
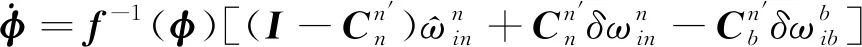
(3)
速度誤差方程為
(4)
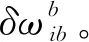
(5)
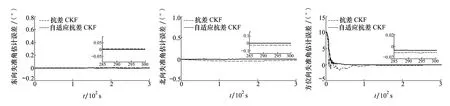
假設系統狀態量為
陀螺及加速度計的白噪聲為
速度和位置信息為
則系統狀態方程和量測方程可以表示為
(6)
式中:Gw是干擾的輸入矩陣,f(x(t),t)和Gw之間的關系如公式(5)所示;h(t)是量測陣,且有h(t)=[02×3I2×202×5];v(t)是量測干擾,w(t)是過程干擾,這2種都服從于v(t)~N(0,R)分布形式。
2 抗差Kalman濾波算法
在SINS/GPS初始對準中,粗差將對最終估計結果產生影響,個別較大的粗差會使結果偏差惡化[2-3,8]。傳統Kalman濾波不能對粗差進行有效處理[9-11]。為了解決上述難題,本文提出了一種基于抗差Kalman的SINS濾波算法。穩健M估計在抗差估計理論中十分實用,所以本文的算法便是以這種估計方法為基石,同時為了轉化為最小二乘形式,算法還使用了等加權原理。抗差Kalman濾波的關鍵是權因子的選擇,而觀測干擾協方差陣的方法經常會使粗差的影響權重變大。因此,本文采用權函數來取代上述方法從而減小或者消除這種影響。
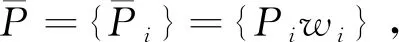
wi=
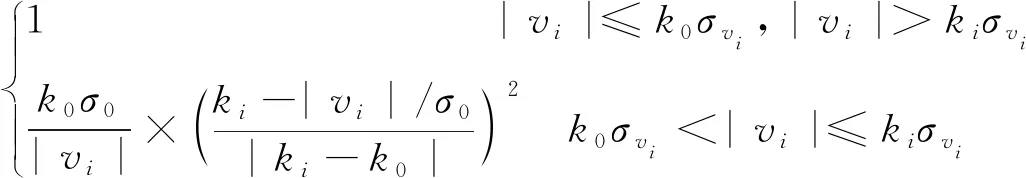
(7)
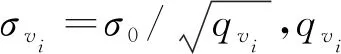
3 自適應抗差CKF濾波算法
3.1 基于自適應Kalman濾波算法設計
不準確的干擾特性通常會使濾波不穩定,甚至發散,因此諸多學者對自適應濾波技術進行了研究[11-13]。在諸多算法中,從計算復雜度、算法復雜度等多角度進行對比,Sage-Husa次優無偏極大后驗(MAP)噪聲估值器具有更低的計算復雜度和算法復雜度,因此被廣泛研究[14]。然而,Sage-Husa噪聲估值器不能同時估計系統和量測受到的干擾,否則會導致濾波發散[15]。在實際環境中,量測受到的干擾可由傳感器的物理特性得到,但由于測量儀器精度、外界干擾等因素影響,系統受到的干擾則很難準確獲得。為了解決上述問題,同時提高系統的自適應能力,本文以協方差匹配為基礎設計了自適應衰減因子。
1) 系統干擾估計算法
本文利用改進的Sage-Husa對不易計算的系統所受干擾qk和Qk進行估計
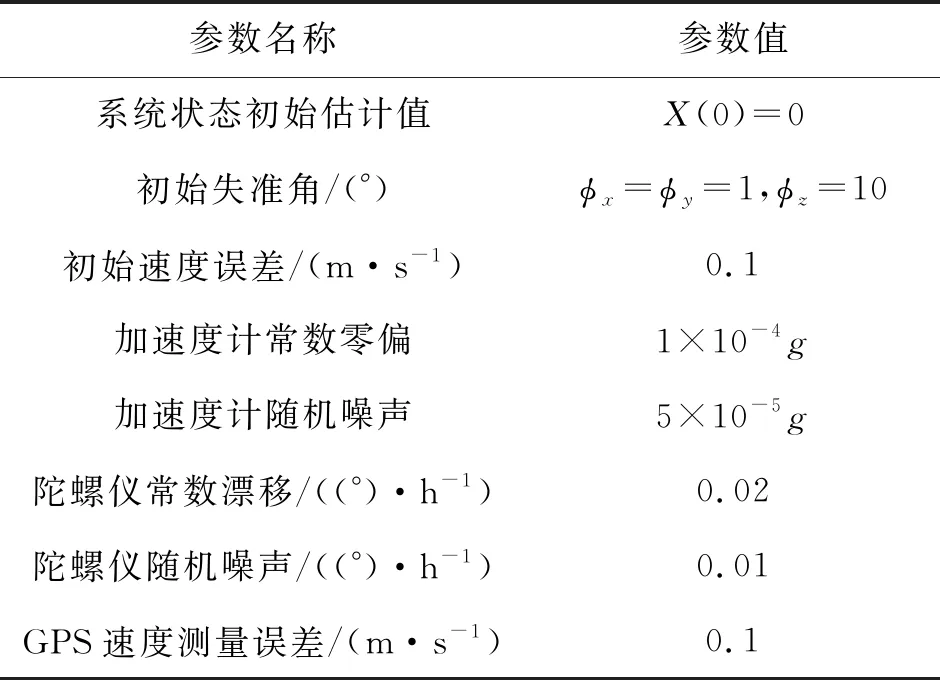
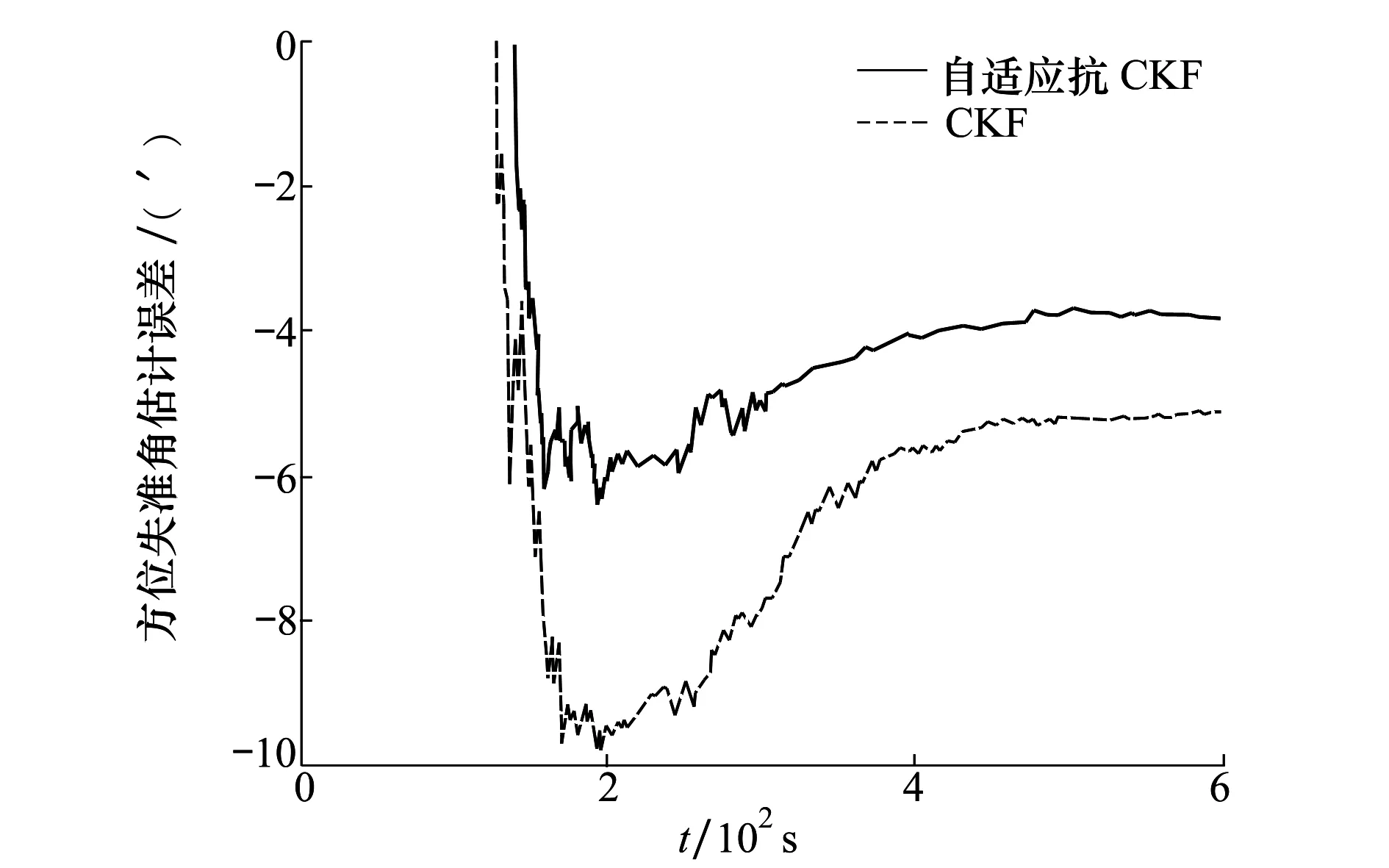
式中,dk-1=(1-b)(1-bk),0.95 2) 濾波發散抑制算法 (10) (11) (12) (13) 式中:0<ρ≤1是衰減系數,一般取值為0.95左右;ρ的值越大,當前殘差向量的影響越大。 不準確的系統干擾會給濾波收斂帶來影響,為解決該問題,本文利用自適應抗差理論對容積卡爾曼濾波(CKF)進行了改進優化。 首先,對于非線性系統來說,設定其狀態方程和量測方程為 (14) 式中,wk-1和vk為互不相關均值為零的高斯白噪聲,且方差陣分別為Q和R。 本文提出的基于自適應抗差CKF算法的改進初始對準方法如下: step1 容積點和權值計算 (15) step2 時間更新 step3 量測更新 (26) (27) step4 發散判斷 (28)式是發散的判斷依據,如果根據公式判斷發散就按照(29)~(32)式修正Pk/k-1,如果不發散就繼續下一步。 針對本文提出的基于自適應抗差CKF算法的改進初始對準方法,設計對應的仿真測試方法,并對其濾波性能進行測試。 首先,對仿真參數進行設定,如表1所示。 表1 仿真參數表 根據上述參數,系統初始方差矩陣P(0)、系統所受干擾矩陣Q和量測所受干擾矩陣R分別為: P(0)=diag{(1°)2,(1°)2,(10°)2,(0.1 m/s)2, (0.1 m/s)2,(0.02°/h)2,(0.02°/h)2,(0.02°/h)2, (1×10-4g)2,(1×10-4g)2} Q=diag{(0.01°/h)2,(0.01°/h)2,(0.01°/h)2, (5×10-5g)2,(5×10-5g)2,0,0,0,0,0}; R=diag{(10 m)2,(10 m)2,(0.1 m/s)2, (0.1 m/s)2} 1) 在某段時間內,速度觀測量增加3 m/s粗差,且在對濾波采樣時進行頻率增加,設置仿真時間為300 s,分別比較2種方法。仿真結果見圖1~3。 根據圖1和圖2,CKF算法收斂時間依次為241.355,18.675 s,誤差精度絕對值依次為0.026°,0.008°;本文提出的抗差CKF算法收斂時間依次為0.001,0.001s,誤差精度絕對值依次為0.003°,0.002°,則本文方法在收斂時間上具有明顯優勢,在誤差精度方面也相比未加入抗差的算法精度高。根據圖3,在方位失準角估計方面,CKF算法收斂時間為228.425 s、誤差精度為0.471°;抗差CKF收斂時間為45.355 s、誤差精度為0.017°,表明抗差CKF具有更高的估計精度和更快的收斂速度,并且濾波更穩定。 圖1 東向失準角估計誤差曲線 圖2 北向失準角估計誤差曲線 圖3 方位失準角估計誤差曲線 2) 基于第1)組仿真條件,假定Q′=10Q,分別比較加入抗差和未加入抗差的2種方法,仿真時間300 s。仿真結果見圖4~6。 圖4 東向失準角估計誤差曲線 圖5 北向失準角估計誤差曲線 圖6 方位失準角估計誤差曲線 根據圖4至6,CKF算法收斂時間依次為0.006,250.148,140.635 s,誤差精度依次為0.005°,0.031°,0.114°;本文提出的抗差CKF算法收斂時間依次為0.001,0.001,38.112 s,誤差精度依次為0.002°,0.002°,0.065°,則對于東向失準角,抗差CKF和自適應抗差CKF估計精度相差不大;對于北向失準角和方位失準角,加入抗差之后的算法的估計精度明顯低于同時加入自適應和抗差的算法。 針對2次測試結果,最終收斂的誤差精度抗差CKF算法更高,收斂速度更快,能夠更好滿足當前對失準角估計的實際使用需求。 在實物測試中,選取某次SINS實測數據,為了驗證本文提出的算法的實際可行性,對數據進行離線分析,得到了圖7的試驗結果。 從圖7可以得知,在此次SINS試驗中,自適應抗差CKF算法收斂于-3.82′,CKF算法收斂于-5.11′,則自適應抗差CKF算法性能更好。因此,本文提出的算法可以有效降低不準確的系統干擾特性以及異常量測信息引起的測量誤差,改善了系統的初始對準精度。 圖7 方位失準角估計誤差曲線 本文提出了一種基于自適應抗差CKF算法的改進初始對準方法,該方法用于解決初始對準中失準角過大情況下觀測粗差和不確定系統干擾造成的誤差影響。通過仿真實驗和實物測試驗證了本文方法的有效性及其在初始對準中具有更強的濾波穩定性、更高的濾波估計精度和更短的算法收斂時間,進而顯著提升了初始對準效率。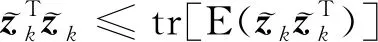
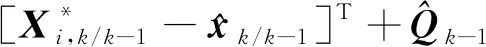
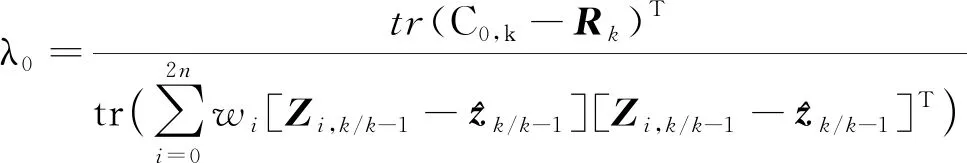
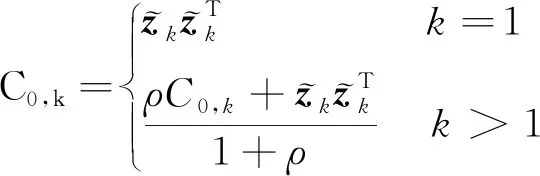
3.2 基于自適應抗差的改進設計
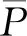
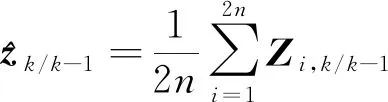
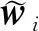
4 驗證與分析
4.1 仿真測試與驗證

4.2 實物測試與驗證
5 結 論

