晶體相場方程的高精度 Fourier 擬譜逼近

羅 原 吳燕梅

(西南科技大學理學院 四川綿陽 621010)

晶體相場模型是由Elder等[1]提出的能夠在原子尺度和擴散時間上模擬材料微觀結構的新方法, 是傳統的連續相場模型的延伸及推廣, 用以填補連續模型與分子動力學方法之間的空白。 該模型能夠耦合多重晶粒位向和彈塑性形變現象, 與傳統的密度泛函理論密切相關[2]，因此在研究晶體微觀結構缺陷和大空間尺度下模擬材料微結構變化更具優勢。模型的能量泛函為：

(1)

其中，Ω=[0,L]×[0,L]∈R2,u:Ω→R表示密度, 一般情況下ε取小于1的常數。晶體相場方程的類型較多, 本文主要研究基于能量泛函式(1)在質量守恒約束條件下導出的H-1梯度流：

ut=Δμ

(2)

(3)

假設u,Δu和μ在Ω上都滿足周期邊界條件，容易驗證能量泛函式(1)隨時間變化保持單調遞減。

由于晶體相場方程(2)是高階非線性偏微分方程, 如何突破對時間步長的苛刻限制是該方程數值模擬面臨的挑戰。Elder等[1]采用顯式歐拉格式進行模擬, 但顯式格式在穩定性上要求時間步長Δt～O(h6)(h為空間步長)，導致此類格式對于長時間數值模擬基本是不可能的。全隱式格式雖然能增加時間步長, 但大部分算法在時間層上的精度不高。因此, 目前所研究的格式大部分都是半隱格式, 這樣既能夠在一定程度上放寬時間步長約束, 又能夠提高逼近精度, 同時又保證了數值格式的能量穩定性。Backofen等[2]采用后向歐拉格式進行模擬,對非線性項采用線性化逼近，但沒有給出嚴格的穩定性分析。Gomez等[3]利用修正的Crank-Nicolson方法，給出具有二階精度的非線性數值格式和相應的穩定性分析。 Wise等[4]和Hu等[5]利用凸分解思想提出二階精度的有限差分格式，較完整證明了格式的質量守恒性、數值解的存在唯一性以及格式的能量穩定性和收斂性。Lee等[6]將晶體相場方程分解為線性和非線性兩部分,提出算子分裂格式,但在能量穩定性上沒有給出具體分析。Vignal等[7]采用二階有限元方法, 并在理論上對格式的質量守恒和能量穩定性進行了較詳細分析。更多二階時間精度的數值算法的研究,可參看文獻[8-11]。為了較全面展現相變量的演化過程,晶體相場方程的數值模擬是相當耗費時間的,因此無論在時間上還是在空間上,高精度的數值格式對于方程的模擬是非常重要的。在時間高精度數值方法上, 相關的文獻并不多見。Shin等[12]利用凸分裂的思想給出了三階精度的凸分裂龍格-庫塔格式,同時分析了格式的能量穩定性。

本文主要針對晶體相場方程(2)-方程(3)的離散，在時間上采用三階的后向差分公式，在空間上用Fourier 擬譜逼近，構造時間和空間上都具有高階精度的數值格式。為保證計算格式的能量穩定性,額外增加Douglas-Dupont正則項。在理論上對數值解的質量守恒性、存在唯一性以及數值格式的能量穩定性給出了詳細分析，數值算例驗證了格式的高精度以及晶體相場方程的長時間動力學模擬的有效性。

1 Fourier擬譜逼近

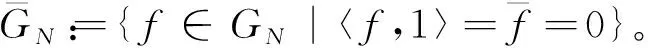
(4)

如果f∈GN, 它的有限離散Fourier展開式為：

(5)

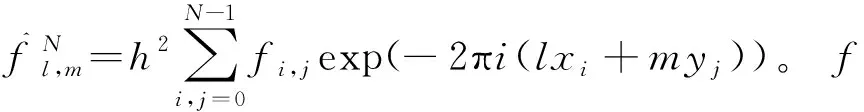
(6)

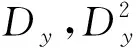
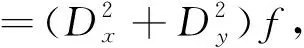
(7)

顯然，▽N·▽Nf=ΔNf。

對網格函數f∈GN，引入離散算子(-ΔN)γ,γ>0，則:

(8)

(9)

利用離散的分部積分公式可以證明如下結論都是成立的：

(10)

〈f,g〉-1,N=〈f,(-ΔN)-1g〉=〈(-ΔN)-1/2f,(-ΔN)-1/2g〉

(11)

所以‖·‖-1,N可以定義為：

(12)

基于上述定義, 可以得到晶體相場方程能量(1)的離散形式，即對于任何的周期網格函數u∈GN,離散能量為：

(13)

2 數值格式以及可解性和能量穩定性

根據晶體相場模型的能量泛函結構, 基于凸分裂的思想, 把能量泛函分解為凹凸兩部分。晶體相場方程中對應的凸項采用隱式處理, 而凹項部分采用顯式處理。方程(2)-方程(3)中時間離散采用三階向后差分離散, 空間上用Fouier擬譜逼近。為保證數值格式的能量穩定性和便于數值計算，對凹項顯式處理項進行外推, 增加Douglas-Dupont正則項, 得到如下具有精度O(Δt3+hm)的計算格式(m表示空間譜精度的階數):

(14)

(15)

(16)

式(14)-式(16)是一個三步格式, 而已知的初始層數據只有u0, 必須尋求其他的方法確定虛擬層u-1,u-2的值。如果設定u-1=u-2=u0, 能量穩定性的分析比較容易，但初始層數據沒有誤差會導致計算結果在初始階段三階時間精度蛻化。當然, 也可以選擇其他高精度的格式如三階或者四階的龍格-庫塔格式計算u1,u2, 能夠保證精度不會損失。

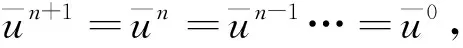
證明：對于式(14)中的ΔNμn+1, 根據周期邊界條件, 利用離散分部積分公式可以得到：

(17)

定理2：如果數值格式式(14)- 式(16)中un,un-1,un-2∈GN, 則式(14)- 式(16)存在唯一解un+1。

證明：令

(18)

(19)

非線性方程(18)能夠看作下述離散能量泛函的極小值：

(20)

根據凸優化理論, 該泛函是嚴格凸的, 因此該泛函的極小值是存在且唯一的, 也就表明式(14)- 式(16)的數值解也是存在且唯一的。證畢。

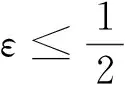
(21)

(22)

證明：將式(14)與(-ΔN)-1(un+1-un)作內積, 得到：

(23)

對上式中的第一項, 可以推出：

(24)

采用離散的分部積分公式及等式(5), 對于非線性項, 得到估計：

女子處于土狼的包圍與攻擊中，跌跌撞撞，險象環生。體力的流逝，令出刀的速度和力量都大打折扣，甚至很難再對土狼造成致命的傷害。

(25)

類似式(16)的分析, 可以得到：

(27)

而且, 如下3個等式也是顯然成立的:

(28)

(29)

(30)

將式(25)- 式(30)代入式(23), 可得：

利用不等式：

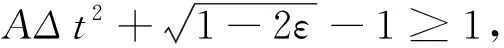
(32)

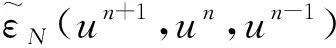
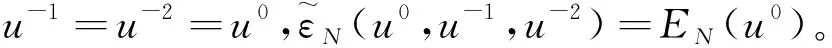
3 數值算例

3.1 時間和空間精度測試

將空間二維計算區域設為Ω=[0,1]×[0,1], 相變量的精確解為:

(33)

此時方程(2)的右端不再是0，而是必須增加一個對應的外力項f(x,y,t), 即：

(34)

對時間層上的誤差估計, 需要把空間譜精度帶來的影響減少到最小。取空間方向網格劃分數N=256, 使得空間譜精度的誤差可以忽略。為比較不同參數組合下的誤差，選擇兩個參數A和ε的不同組合, 計算終止時間取t=1。為方便收斂階測試, 時間步長從0.1開始依次減半, 相變量u的數值解的‖·‖2誤差及收斂階數的計算結果見表1。

表1 不同參數下時間方向的‖·‖2誤差及階數Table 1 The‖·‖2 errors and orders in temporal direction with different parameters

從表1結果可以看出, 盡管理論上對系數A的要求極高, 在數值模擬時卻沒有這一限制條件。無論是A=1,A=10還是A=20,都沒有滿足定理3中的條件, 但是計算結果的精度非常高。另一方面, 隨著A值不斷增加, 絕對誤差越來越大, 這是因為A越大會產生更大的數值耗散。

對于空間方向的誤差估計, 選擇A=1,ε=0.025以及時間步長Δt=10-4。 時間步長取這么小的原因也是不希望時間層上的誤差給空間誤差的驗證帶來過多的干擾。 計算終止時間t=1，誤差結果見表2。顯然，Fourier譜精度隨著空間網格劃分數N的增加快速提升, 但是后期無論N值怎么增加, 精度都沒有大幅提高, 因為此時已經不是空間離散誤差而是時間離散誤差占據主要作用。

表2 空間方向的‖·‖2誤差 Table 1 The ‖·‖2 errors for the spatial direction

3.2 晶體相場方程的動力學數值仿真

設二維空間區域為Ω=[0，128]×[0，128], 數值格式式(14)- 式(16)中的參數選取為A=2,ε=0.025, 空間步長固定為h=1, 晶體相的初始狀態值為：

ui,j=0.06+0.03ri,j

(35)

其中ri,j為[0,1]服從均勻分布的隨機數。為提高計算效率, 采取不同的時間步長進行數值模擬, 即在時間區間[0,100]上取Δt=0.01, 在[100,2 000]上取Δt=0.1, 晶體相場的動態演化在不同時間的狀態見圖1。

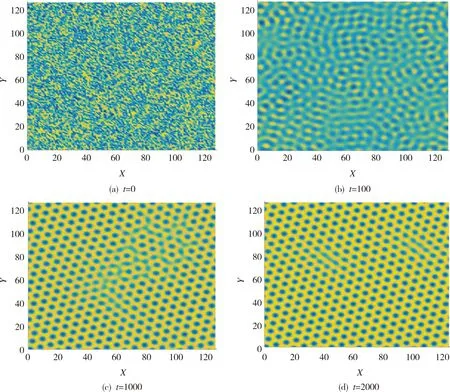
圖1 不同時刻晶體相場的狀態圖Fig.1 State diagram of the crystal phase field at different times

圖2給出不同時刻下的離散能量和離散質量的計算結果。 可以看出離散能量的變化和理論一致, 即保持單調不增。前一段由于時間步長較小, 使得圖2中能量變化和時間步長較大的后一段相比較為平緩；中間段能量的變化較劇烈, 但隨著能量衰減到一定程度, 能量變化呈現出平緩狀, 此時晶體的相或者密度分布基本處于平穩狀態。質量隨著時間的變化，始終保持恒定，也驗證了定理1的正確性。

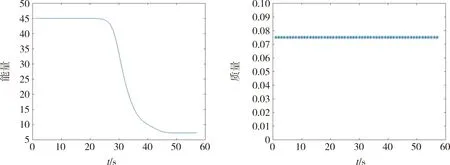
圖2 晶體離散能量和離散質量的動態演化圖Fig.2 Dynamic evolution of the crystal discrete energy and discrete mass

4 結論

本文結合晶體相場模型的能量泛函結構, 利用凸分裂思想, 對周期邊界條件的晶體相場方程提出了一種具有能量穩定性的數值算法。算法在空間上采用Fourier擬譜逼近，在時間采用上后向差分的三階精度逼近, 并增加Duglas-Dupont正則項以保證數值格式的能量穩定性。對數值格式解的存在唯一性以及格式的能量穩定性進行了證明，采用數值仿真驗證了格式在時間上的三階精度和空間上譜精度, 并給出了方程的長時間動力學演化模擬。