12.3 角的平分線的性質 教學設計

焦麗英

學習目標：

1.從“公路”的具體情境中，抽象出幾何模型，初步感悟“具有某條件的點的特征”.

2.類比平行線，探索并證明角的平分線的性質.

3.在探索活動中，體會合情推理的作用，理解模型思想、集合思想.

4.通過對定理證明的一般步驟的梳理，體會數學的嚴謹性，發展邏輯推理能力.

學習重難點：

重點：探索并證明角的平分線的性質

難點：證明以文字形式給出的角的平分線的性質

學習活動設計：

一、借助情境，發現問題

情境1：秋天的中國是色彩斑斕的、最美的，國慶節期間，有很多人會出去旅游，欣賞祖國的大好河山。在旅游圖中拍了這樣一張照片，公路兩上的兩條白線互相平行，最中間一條黃線的位置是如何確定的？

師生活動：學生觀察圖片后，從實際情境中抽象出數學問題，畫出圖形，并確定黃線的位置.教師適當追問，引導學生分析“中間的線”“到兩平行線距離相等的點”之間的關系，明確應從兩個角度去探究問題.

【活動1】畫出兩平行線間的“中間的線”并簡要記錄畫圖步驟.

設計意圖：通過實際情境引入，激發了學生的學習興趣;借助情境，學生經歷將實際問題抽象為數學問題的過程，從更易于理解的平行線間“中間的線”開始探究起，逐步分析出兩個猜想，既要研究直線上所有的點都滿足一定條件，還要研究滿足特定條件的所有的點都在直線上，既為下一個環節探究角的平分線的性質做了鋪墊，又讓學生獲得一定的研究經驗.

二、問題變式，類比探究

情境2：如果公路很長很長，則抽象成一個角，這時你還能找到中間的線么？

問題1：當兩直線不平行時，“中間的線”還存在嗎？它有名字嗎？

問題2：角的平分線有與“中間的線”有相類似的性質嗎？

【活動2】提出關于角的平分線的猜想.

類比兩平行線間“中間的線”的猜想，提出角的平分線的兩條猜想：猜想1——角的平分線上的點到角的兩邊的距離相等;猜想2——角的內部到角的兩邊距離相等點在角的平分線上.

設計意圖：情境由兩條平行的直線變為一個角，學生能夠在這種特殊到一般的變化中，主動的運用類比的方法，較為順利地提出對角的平分線的性質的兩條猜想.

三、證明猜想，歸納小結

【活動3.1】將命題1改寫成符號語言.

分析命題1的條件和結論，明確命題1的研究對象是線上的點;借助量角器，畫出角的平分線，再將命題的條件、結論分別用符號語言表述出來.教師展示學生的作圖，并請一名學生簡要描述自己的作圖步驟，師生共同辨析得出大家都認可的一種恰當的表述.

設計意圖：學生經歷猜想——畫圖——改寫——證明這一系列探究的過程，初步獲得研究幾何問題的方法和步驟.

在將命題的文字表述轉化成符號語言的過程中，學生可能會出現不同的理解.

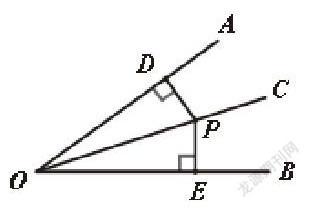
預設1：已知，如圖，∠AOC=∠BOC，點P在OC上，PD⊥OA于點D，PE⊥OB于點E.求證：PD=PE.

預設2：已知，如圖，∠AOC=∠BOC，點P在OC上.求證：PD=PE.

預設3：已知，如圖，射線OC平分角∠AOB，點P在射線OC上.求證：點P到OA、OB的距離相等.

學生在將文字改寫成符號語言時，對于如何描述距離出現不同的理解，教師引導學生分析幾名同學的改寫，確定預設1中的書寫是最為恰當的表述.

【活動3.2】完成命題1的證明過程.

學生獨立完成命題1證明過程，在黑板上板演證明的完整過程.

【活動3.3】師生共同歸納證明一個幾何命題的一般步驟：閱讀命題——分析條件和結論——畫出圖形——寫成符號語言——完成證明.

【活動3.4】獨立完成命題2的證明.

四、拓展探究，提高能力

【活動4.1】探究角平分線的畫法.

【活動4.2】拓展作業

特色學習資源分析，技術手段應用說明：

本節課的教學重點是角的平分線的兩條性質定理的探究及證明，角的平分線是到角的兩邊距離相等的點的集合，為了讓學生能夠對角的平分線有更加深刻和完整的理解，教師設計了充分的活動.

首先在情境引入環節，教師沒有直接引入角和角的平分線，而是先由一個實際情境引出了學生更易理解的兩平行線和兩平行線間的“中間的線”，引導學生提出“中間的線”的兩條猜想，再畫圖說明;再將平行線變為相交線，通過類比“中間的線”的研究思路，再來探究角的平分線，分散了角的平分線的性質探究的難點，對提升學生思維有很大的幫助，這種設計思路非常新穎.

教師引導學生從充分性和必要性兩個角度去提出猜想，在整個授課的過程中也都在不斷滲透這種集合思想，很好的訓練了學生思維，對以后數學學習起著很重要的作用.

教師在授課前，對八年級的學生進行了充分的調研和學情分析，基于學生的問題，設計學生活動，有的放矢，課堂上讓學生充分的參與和展示，真正的做到了以學生為本.