初中數學問題解決再思考

廖麗民

[摘 ?要] 在初中數學教學中，問題解決是一個非常關鍵的問題，它有兩層含義：一是狹義的問題解決，是指與數學知識直接相關的數學問題或者數學習題的解決;二是廣義的問題解決，是指一種思維方式，或者是指一種思維過程，其更傾向于認知的一面. 在具體的教學過程中，教師可以通過學生的思維結果去判斷他們的思維過程，這樣就可以更好地實現因材施教. 而從核心素養培育的角度來看，把握了學生的思維特點，就可以讓學生在問題解決的過程中，更好地進行數學抽象與邏輯推理，于是數學學科核心素養的培育，也就可以在問題解決的過程中實現.

[關鍵詞] 問題解決;教學思考;數學學科核心素養

在初中數學教學中，問題解決是一個非常關鍵的問題，對于數學教師而言，問題解決有兩層含義：一是狹義的問題解決，是指與數學知識直接相關的數學問題或數學習題的解決，在解決這個問題的過程中，學生根據數學問題或數學習題給出的信息，直接運用數學知識，搭建起從未知到已知的橋梁，這標志著學生成功地解決了問題;二是廣義的問題解決，指一種思維方式，或者指一種思維過程，其更傾向于認知的一面，強調在解決具體問題的過程中，形成一種良好的解決問題的思維方式或學習習慣. 認識到這兩層含義，循序漸進地教學數學，就可以有效地培養學生理解與運用數學知識的能力，同時也能幫他們形成良好的數學學習習慣，這對于培育他們的數學學科核心素養是非常有幫助的. 問題解決本來是初中數學教學中一個比較傳統的話題，此前更是寫進了《義務教育數學課程標準》，今天在數學學科核心素養的視角之下思考問題解決的價值，有著更為深遠的現實意義.

問題解決的認知機制分析

傳統數學教學對問題解決的狹義理解已經研究得非常充分，本文更多的是在廣義理解的基礎上，結合數學學科核心素養培育的需要，談談筆者的一些認識. 而認識的切入點首先是問題解決的認知機制，眾所周知，在初中數學教學中，若從能力要求上看，則要求學生解決的數學問題涉及的數學內容領域更加綜合，數學問題情境更加貼近學生生活，解決數學問題的認知要求也逐步升高. 而能力與核心素養是密切相關的，核心素養特別強調培養學生適應社會發展與終身發展的關鍵能力（除此之外還有必備品格），那么問題解決在關鍵能力培養上有什么作用呢？其對數學學科核心素養的組成要素又有什么樣的培養作用呢？不妨看一個例子.

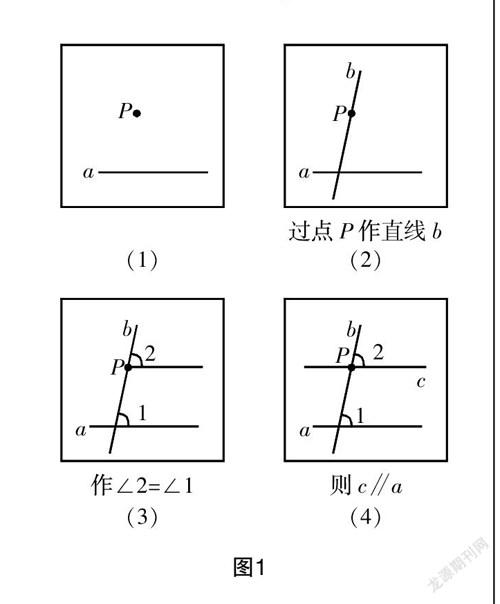
在教學“平行線”時，有“平移”這一內容，“平移”與“平行線”的性質與判定有著密切的聯系，往往是結合一些數學活動而設計聯系情景，比如可以給學生設計這樣一個數學活動：你掌握多少種畫平行線的方法？畫平行線是本知識當中的一個重要技能，而技能的表現為數學能力，技能的背后則是數學思維. 利用“平移”的知識來作平行線，本質上也是一個問題的提出與解決的過程. 如果將這個過程設計成開放形式的，那不同的學生的選擇是不一樣的，有學生會根據平行線的判定如“同位角相等，兩直線平行”去畫平行線，如圖1.

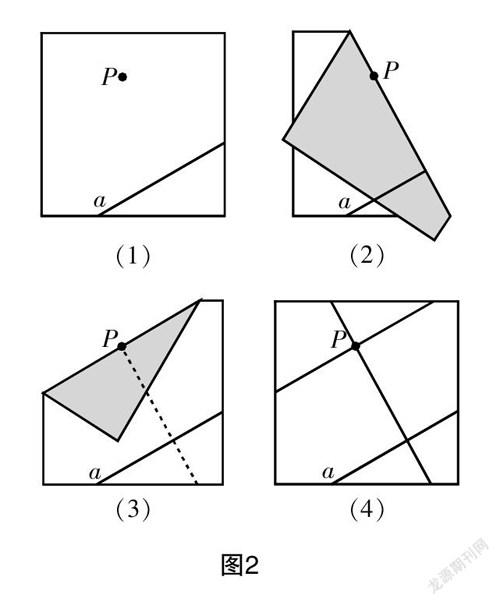
而有的學生可能會通過折疊的方法，如圖2. 這是一種別出心裁的方法，但背后也有著邏輯思維的支撐.

梳理這兩種不同方法背后的問題解決思維，會發現各自有所不同：前者是對平行線的判定知識的直接運用，后者是在對平行線的性質與判定知識理解的基礎上，用折疊的方法表現出判定兩直線平行的性質. 因此這里對知識的理解與運用，實際上就反映著問題解決中的認知機制.

問題解決的學生思維分析

研究問題解決的認知機制，實際上是為了更好地分析學生的思維. 從宏觀層面的角度看，中學數學問題解決中數學思維的辯證運用是指在解決數學問題時，學生根據已知條件運用辯證唯物主義中的普遍聯系、對立統一、量變和質變等原理思考同一種數學思維的不同思維形式之間或不同數學思維之間的關系，以有效地組織思維，達到解決問題的目的. 對于初中數學教學而言，這樣的理解可以進一步細化，將之與學生的問題解決過程聯系起來，去搭建一個分析學生思維的框架.

如結合上面的例子，學生采用平行線判定的性質去畫平行線，這種問題解決背后的思維，是大多數學生表現出來的一種思維方式，因為“如何畫平行線”這個問題，與“平行線的判定”之間幾乎是一種直接的因果關系. 學生只要理解了后者，就自然能夠想到用這種方法去完成前者問題的解決.

而通過折疊的方式來畫平行線，相較而言就是一種比較獨特的思維，從形式上來看，他不是采用直接畫的方式來完成問題的解決的，而是對平行線的判定在大腦當中進行深度加工，將“畫”改成了“折疊”，折疊本身就已經體現了平行線判定的邏輯，最后的“畫”其實只是對折疊痕跡的素描而已. 筆者認為這一類學生具有強大的空間想象能力，有著強大的表象建構能力，這種能力往往能夠讓他們通過直觀想象、合情推理等，去完成問題的解決.

在教學過程中，教師可以通過學生的思維結果去判斷他們的思維過程，把握他們的思維特點，這樣就可以更好地實現因材施教. 而從核心素養培育的角度來看，只要把握了學生的思維特點，就可以讓學生在解決問題的過程中，更好地進行數學抽象與邏輯推理，于是數學學科核心素養的培育，也就可以在問題解決的過程中實現.

問題解決的方法運用分析

對于初中學生而言，問題解決的過程是需要體驗的，因此問題解決不宜以明確的定式來進行顯性的教學. 那么對于教師而言，如何指導學生進行問題解決方法的運用，也值得研究與分析. 這其中有一個“捷徑”，那就是對數學思想方法的運用.

有經驗的教師都知道，數學思想方法是數學問題解決的理論指導. 對于學生而言，這種理論指導作用往往是隱性的，要讓學生在體驗具體的數學思想方法的過程中，認識到它們的價值. 比如說邏輯推理，其實就是根據數學概念之間的邏輯關系，通過分析與綜合的方法，讓學生在解決問題的過程中去體驗這種邏輯關系的運用，這樣就能夠將數學思想方法的體驗與問題解決結合起來，同時又能夠讓學生經歷數學學科核心素養中強調的邏輯推理等過程，于是問題解決自然就成為促進學生核心素養落地的過程.

總之，在初中數學教學中問題解決的價值是非常高的，即使是在核心素養的背景之下，它也能夠成為核心素養落地的一條途徑.