二分類Logistic回歸算法在化妝品功效評價中的應用

王福鑫 矯筱蔓 史延通

【摘要】 本文應用R語言對化妝品功效評價中產生的數據進行了基于二分類Logistic回歸分析。使用逐步回歸方法，發現數據自變量與因變量間的關系與差異，并建立Logistic回歸模型，為今后化妝品功效試驗設計參數的納排方法提供重要參考。

【關鍵詞】 R語言;化妝品功效評價;Logistic回歸

【DOI編碼】 10.3969/j.issn.1674-4977.2022.01.020

Application of Binary Logistic Regression Algorithm in Efficacy

Evaluation of Cosmetics

WANG Fu-xin，JIAO Xiao-man，SHI Yan-tong

（Liaoning Institute of Drug Control，Shenyang 110036，China）

Abstract： In this study，R language is used to analyze the data generated in the cosmetic efficacy evaluation based on binary logistic regression. Using stepwise regression method to uncover the relationships and the difference between independent variables and dependent variables. After that，the logistic regression model was established. The result will play an important role for the inclusion and exclusion methods of cosmetic efficacy evaluation experiment design in the future.

Key words： R language;cosmetic efficacy evaluation;logistic regression

在科學研究中，統計軟件是必不可缺的實用工具。目前較為流行的統計分析軟件是SPSS，然而SPSS功能有較大的局限性，可視化程度也較為簡單。相較于SPSS軟件，R語言以其開源、免費、多平臺、體積小巧、編程簡單、可視化等優點逐漸獲得越來越多科研工作者的青睞。在化妝品功效評價研究中，R語言可幫助研究人員設計試驗方案、進行數據分析和總結。化妝品功效評價研究常涉及眾多目標參數的選擇問題，確定參數間的相關性及差異性對指導后續試驗研究工作尤為重要。以R語言為工具可較為直觀且有針對性地對研究數據進行梳理分析，進而得到模型篩選后的目標參數。

以一種宣稱具有抗衰老功效的化妝品原料為例，多項研究數據顯示，該原料的功效效果存在差異，功效效果綜合評價可選擇有效或無效。為了今后企業開發設計是否添加該原料的化妝品，需要對該原料的多項實驗中涉及的各項數據參數進行統計分析，發現哪些特征參數與功效效果有差異，哪些特征參數之間有相關性。

通過對上述研究內容的了解，二分類Logistic回歸能很好實現研究的要求。二分類Logistic回歸主要研究二元分類響應變量與諸多自變量之間的相互關系。

1 探索性分析

首先，因變量即不同效果用對應的數字表示，不能寫成有效或無效，把有效和無效分別設置成0和1進行操作。研究的數據集包含1584個報告有效結果和1584個報告無效結果的數據樣本（本研究所用數據和特征均為隨機假設，非真實研究結果，僅為演示算法流程）。其中包含20個與皮膚抗衰老有關的特征參數，以其作為自變量。為了更好了解這20個特征參數之間的關系，可通過相關系數熱力圖可視化這20個特征參數之間的相關系數，程序和結果如下（下文數據分析均在R Studio環境下R語言版本4.1.1中進行）：

> library（caret）

> library（ROCR）

> library（tidyr）

> library（corrplot）

> aging<-read.csv（"/Desktop/Antiaging.csv"，stringsAsFactors=F）

> aging_cor<-cor（voice[，1：20]）

> ggcorrplot（aging_cor，method="square"）

使用corrplot包中的corrplot.mixed（）函數，可視化變量之間的相關系數。結果表明，很多特征之間的相關性很強，提示可能具有抗衰老機制的協同或拮抗作用。

> corrplot.mixed（aging_cor，tl.col="black"，tl.pos = "lt"， tl.cex = 0.8，number.cex = 0.45）

通過圖1、圖2可以直觀地顯示20個特征參數之間的相關性，結果表明，很多特征之間有較強的相關性。接下來，使用可視化每個變量在不同功效結果下的密度曲線進行對比區分兩種功效結果所有特征參數的差異，程序和結果如下：

> library（tidyr）

> plotdata<-gather（aging，key="variable"，value="value"，c（-label））

> ggplot（plotdata，aes（fill=label））

+theme_bw（）+geom_density（aes（value），alpha=0.5）

+facet_wrap（～variable，scales="free"）

通過圖3可以發現，在某些特征參數下，抗衰老效果差異很明顯，如CAT，Col-I，MMP-1，ORAC和sd等;有些差異則很不明顯，如AGEs，DPPH，GSHPX等。

2 建立Logistic回歸模型

在了解這些數據特征的關系和差異后，就可以建立Logistic回歸模型對功效結果進行分類。建立Logistic回歸模型可用glm（）函數完成。為強化評估模型的泛化能力，使用數據集的70%作為訓練集建立回歸模型，使用剩余數據（30%數據集）作為測試集檢驗該模型的效果，程序和結果如下：

> aging$label<-factor（aging$label，levels=c（"yes"，"no"），labels=c（0，1））

> library（caret）

> index <- createDataPartition（aging$label，p=0.7）

> agingtrain <- aging[index$Resample1，]

> agingtest <- aging[-index$Resample1，]

> aginglm <-glm（label～.，data=agingtrain，family="binomial"）

> aginglmstep <- step（aginglm，direction="both"）

> summary（aginglmstep）

## Call：

## glm（formula=label～median+MMP.1+AP.1+Col.I+ROS+MDA+

##? ?CAT+GSHPX+AGEs，family="binomial"，data=agingtrain）

## Deviance Residuals：

##? ?Min? ? ?1Q? ? Median? ? 3Q? ? ? Max

## -4.5356? -0.0935? -0.0002? ?0.0277? ?3.2539

## Coefficients：

##? ? ? ? ? Estimate Std. Error z value Pr（>|z|）

## （Intercept）? 16.264823 8.964575 1.814 0.06962 .

## median? ? ?10.819219 5.793547 1.867 0.06184.

## MMP.1?; ? ?-59.369107 5.833076-10.178<2e-16 ***

## AP.1? ? ? ?0.003397 0.001373 2.475 0.01332 *

## Col.I? ? -46.684861 10.689227 -4.367 1.26e-05 ***

## ROS? ? ? 12.690259 2.347499 5.406 6.45e-08 ***

## MDA? ? ? ?-3.807964 2.610757 -1.459 0.14468

## CAT? ? 181.523806 11.689991 15.528 < 2e-16 ***

## GSHPX? -44.233663 10.262250 -4.310 1.63e-05 ***

## AGEs? ? ? 4.452719 1.533414 2.904 0.00369 **

## ---

## Signif.codes：0‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

## （Dispersion parameter for binomial family taken to be 1）

##? ?Null deviance：3074.80 on 2217 degrees of freedom

## Residual deviance：347.82 on 2208 degrees of freedom

## AIC：367.82

以上程序使用step（）函數進行了逐步回歸分析，以該方法可以從20個特征中選擇顯著的特征建立模型。在建立回歸模型后，通過指定的glm（）中的參數family進行Logistic回歸。

結果發現，模型的AIC=368.82，且模型只用了9個變量（median、MMP-1、AP-1、Col-I、ROS、MDA、CAT、GSHPX、AGEs）作為回歸模型的自變量，并且每個變量都是顯著的，可剔除掉其余11個不顯著的自變量。結果說明，這9個特征參數的變化對該原料抗衰老功效效果有顯著影響，可在今后研究中著重研究這9種特征。

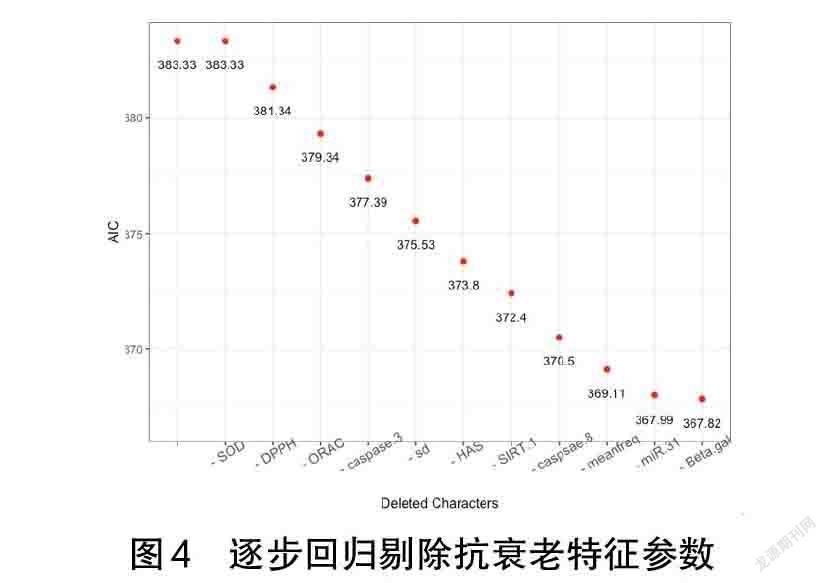
3 逐步邏輯變量篩選過程

在優化Logistic回歸模型中，采用逐步回歸剔除不需要的自變量。利用R可視化逐步回歸（見圖4），觀察過程中AIC值的變化情況，可更直觀地顯示優化狀態。程序和結果如下：

stepanova<-aginglmstep$anova

stepanova$Step<-as.factor（stepanova$Step）

ggplot（stepanova，aes（x=reorder（Step，-AIC），y=AIC））

+theme_bw（base_size=12）

+geom_point（colour="red"，size=2）

+geom_text（aes（y=AIC-1，label=round（AIC，2）））

+theme（axis.text.x=element_text（angle=30，size=12））

+labs（x="Deleted Characters"）

在剔除過程中，AIC值一直在減小，模型的穩定性逐漸增強。例如：剔除SOD這個參數后，AIC值沒有變化。這是因為SOD這個特征參數在原始模型中是使模型奇異的特征，可以由其他特征的線性組合代替。這樣的特征參數存在只會對模型產生不穩定性。

由于Logistic回歸主要針對二元分類響應變量，所以也可用于設置有無某些功效，并把諸多檢測參數引入，建立回歸模型判定哪些指標對該功效影響顯著，進而作為功效評價研究納排指標的重要參考依據。

【參考文獻】

[1] 許汝福.Logistic回歸變量篩選及回歸方法選擇實例分析[J].Chin J Evid-based Med，2016，16（11）：1360-1364.

[2] 劉二鋼，馬建強.R語言在統計分析中的使用技巧[J].Computer Knowledge and Technology，2017，13（1）：251-256.

[3] 張婷婷.Logistic回歸及其相關方法在個人信用評分中的應用[D].太原：太原理工大學，2017.

【作者簡介】

王福鑫，男，1984年出生，主管藥師，博士，研究方向為化妝品功效安全評價。

矯筱蔓，女，1978年出生，主任藥師，碩士，研究方向為化妝品檢驗技術。

史延通，男，1975年出生，研究員，碩士，研究方向為化妝品監管。