鳥類分類問題數學建模實驗研究

彭李嘉

(北京郵電大學 計算機學院，北京 100876)

1 問題的提出

同一片森林里生活著兩種鳥，它們外形相似，習性相近。科研人員分別記錄了這兩種鳥類的翅展(翅膀展開的長度)和身長，如表1所示。

問題一：請根據上述表格，給出一個為這兩種鳥類分類的方法。

問題二：現觀察到該片叢林中的三只鳥，其翅展和身長的數據分別為(12.50，19.00)(13.00，18.00)(14.00，20.70)。請通過數據進行辨識這三只鳥分別是A類還是B類。

問題三：若科研人員發現記錄中有一處錯誤，翅展13.80 cm、身長19.00 cm的這只鳥應屬于A類而非B類，請分析該錯誤對分類的影響。

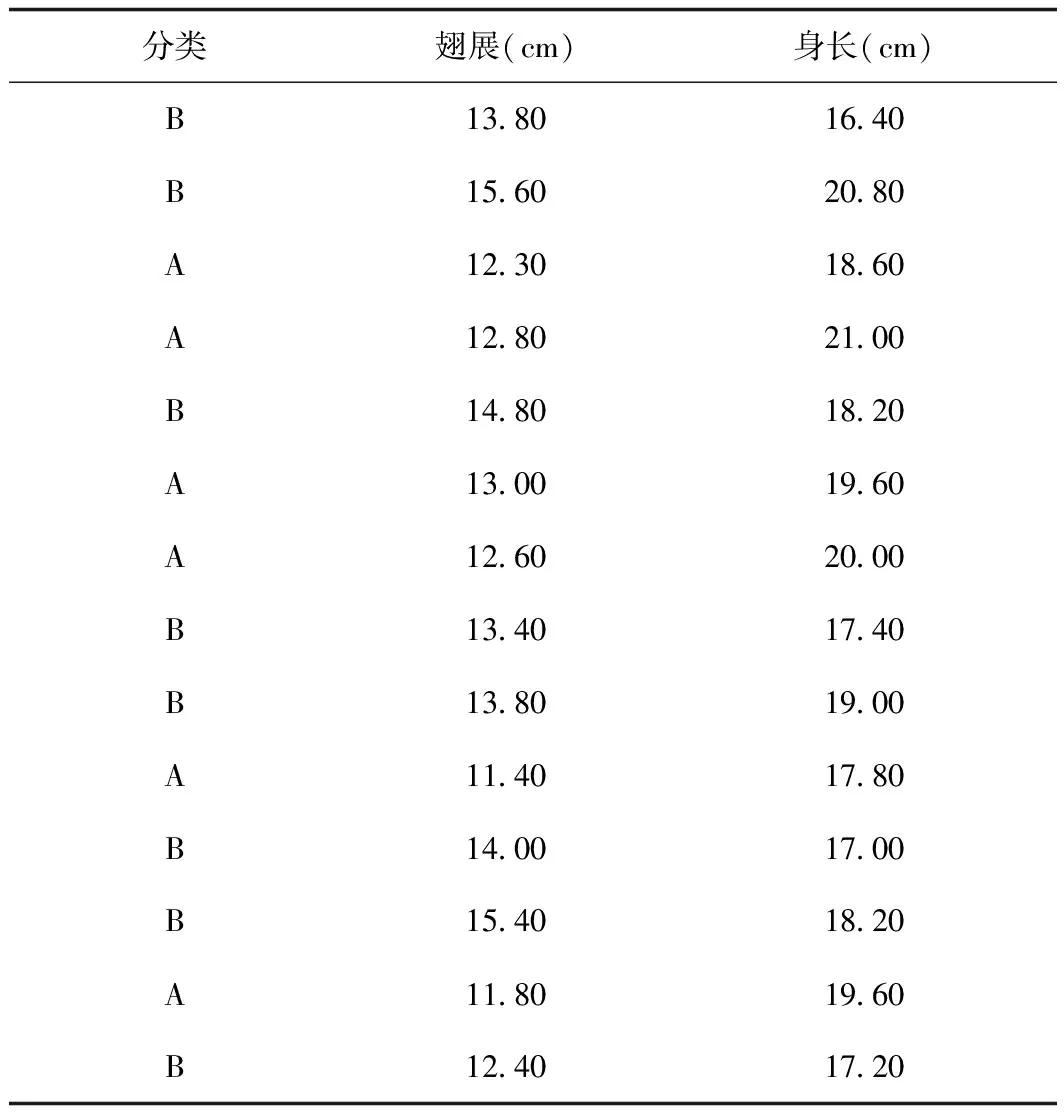
表1 兩種鳥類的翅展和身長Tab.1 Wing expanse and body length of two kinds of birds

2 問題分析

對于問題一，題目要求給出為這兩種鳥類分類的方法，已知數據是鳥的種類及它們的翅展和身長，因此建立的模型要找到種類與翅展、身長的關系。通過對題目中所給數據的初步分析可以看出：整體特征都是隨著翅展長度的增加，鳥的身長也在增加。因此可以認為這兩種鳥類的分類與它們的翅展、身長服從一定的規律。但畫出散點圖之后，自變量之間的關系仍不清晰，因此決定選用逐步分析法找到對因變量有顯著影響的自變量，建立模型并運用殘差分析法改進模型，給出兩種鳥類分類的方法。

對于問題二，題目要求辨識給出的3組數據來確定鳥的分類。問題二的基礎是問題一所求得的模型，因此分別將3組數值代入問題一中的回歸模型，根據求得種類的值確認該鳥屬于哪種類別。

對于問題三，題目要求分析表格中一處錯誤對分類的影響。問題三的基礎同樣是問題一，因此在問題一所求得的模型中，將錯誤數據對應種類的值進行修正，改正后重新建立模型，將新模型所得結果與問題一的結果進行對比，根據兩者的差異分析該錯誤對于分類的影響。

3 模型的假設與符號說明

3.1 模型的假設

假設一：不考慮除翅展、身長之外的其他因素對于分類的影響。

假設二：假設數據中每一只鳥都是純種鳥，不考慮A、B兩種類別鳥的雜交后代及A、B兩種類別鳥與其他鳥類的雜交后代。

3.2 符號說明

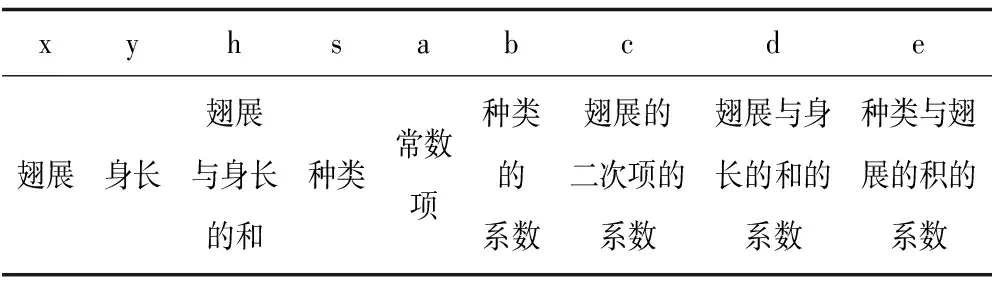
表2 符號說明Tab.2 Symbol description

4 模型的建立與求解

4.1 問題一的模型建立與求解

4.1.1 問題一的模型建立

將題目中所給的兩類鳥數據按照翅展的值從小到大進行排序。

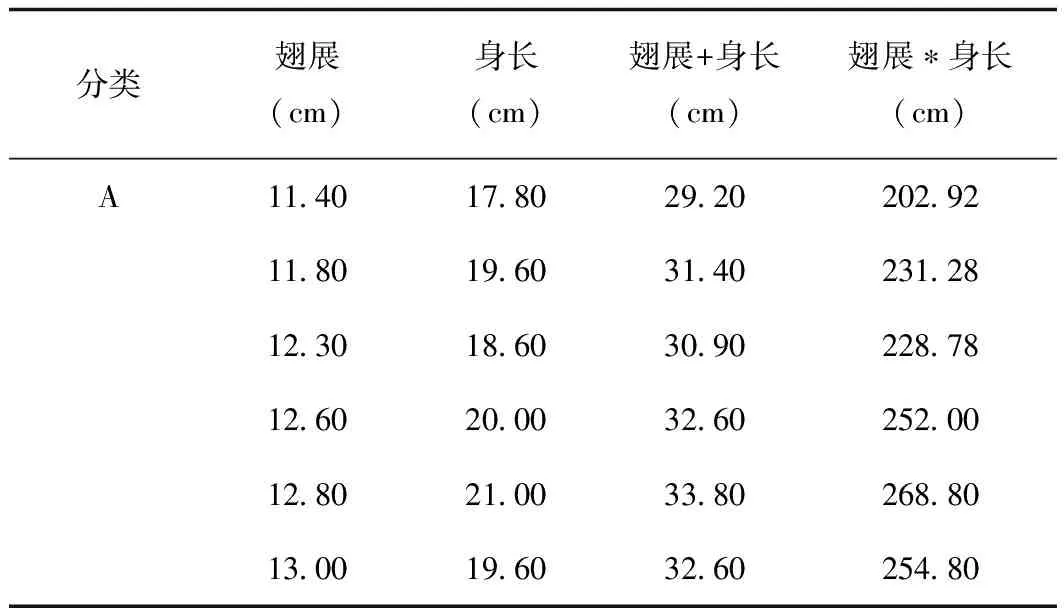
表3 A類鳥翅展值的排序Tab.3 Order of wing expanse value of A type birds

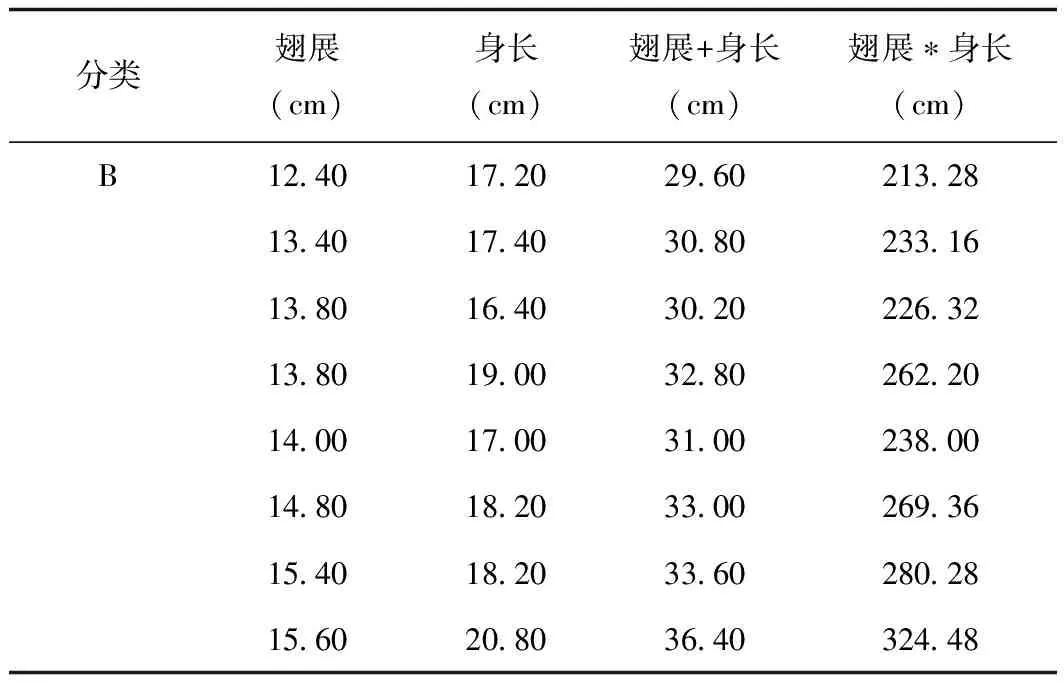
表4 B類鳥翅展值的排序Tab.4 Order of wing expanse value of B type birds

利用matlab軟件畫出散點圖。

a.橫軸為翅展，縱軸為身長。

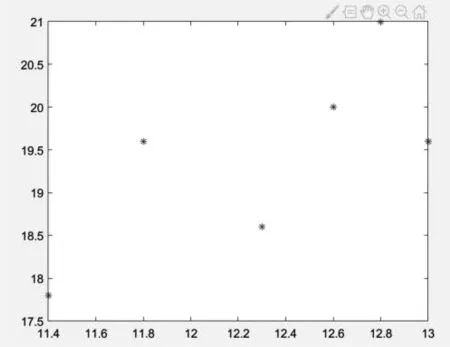
圖1 A類鳥散點圖Fig.1 Scattered plot of A type birds

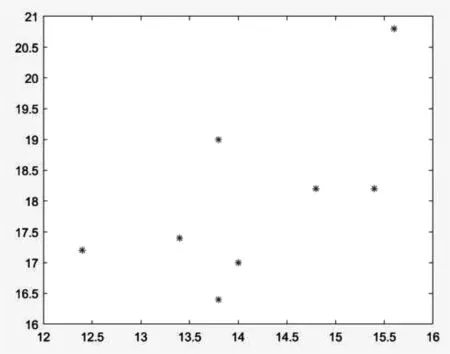
圖2 B類鳥散點圖Fig.2 Scattered plot of B type birds

b.橫軸為翅展+身長，縱軸為身長。

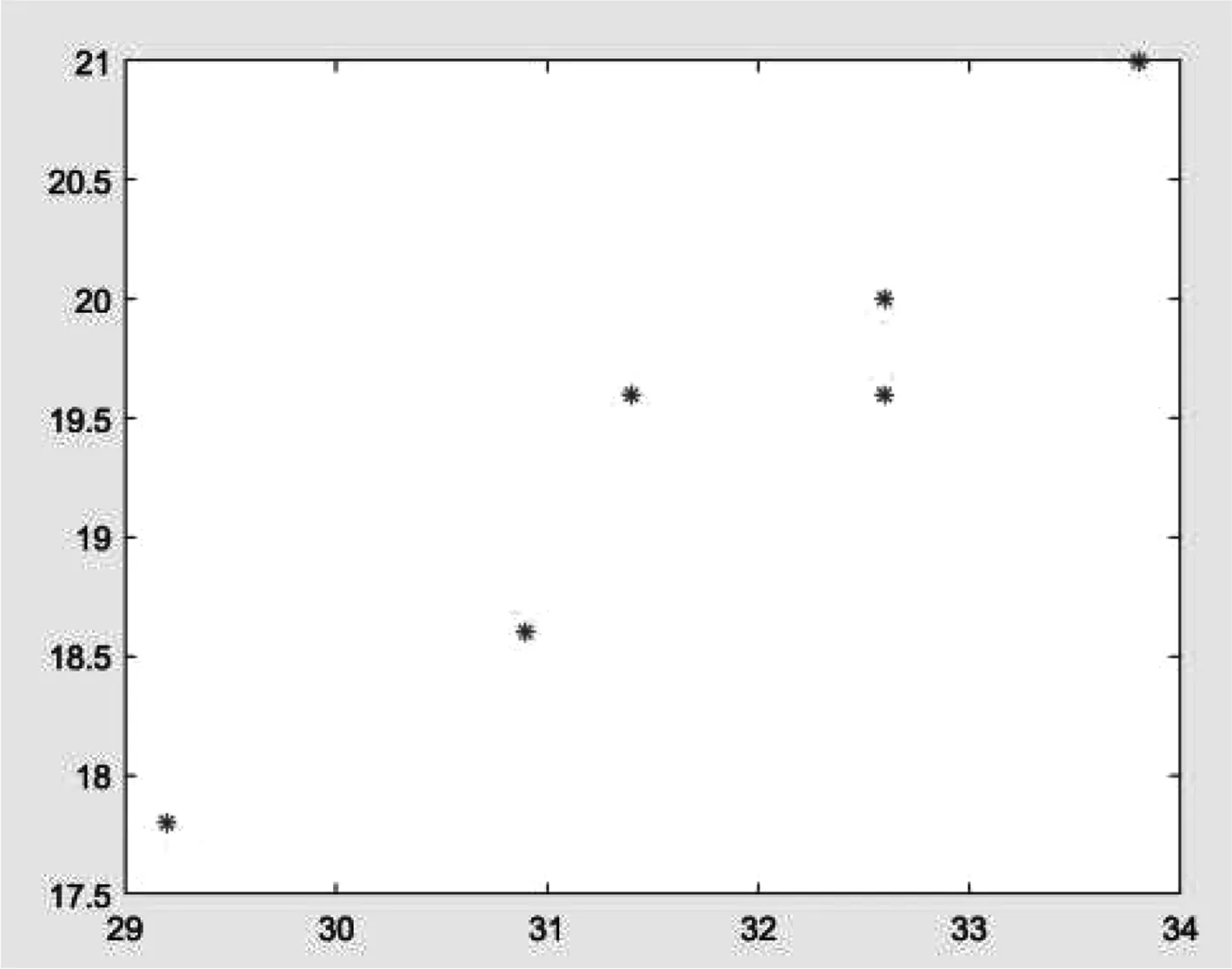
圖3 A類鳥散點圖Fig.3 Scattered plot of A type birds

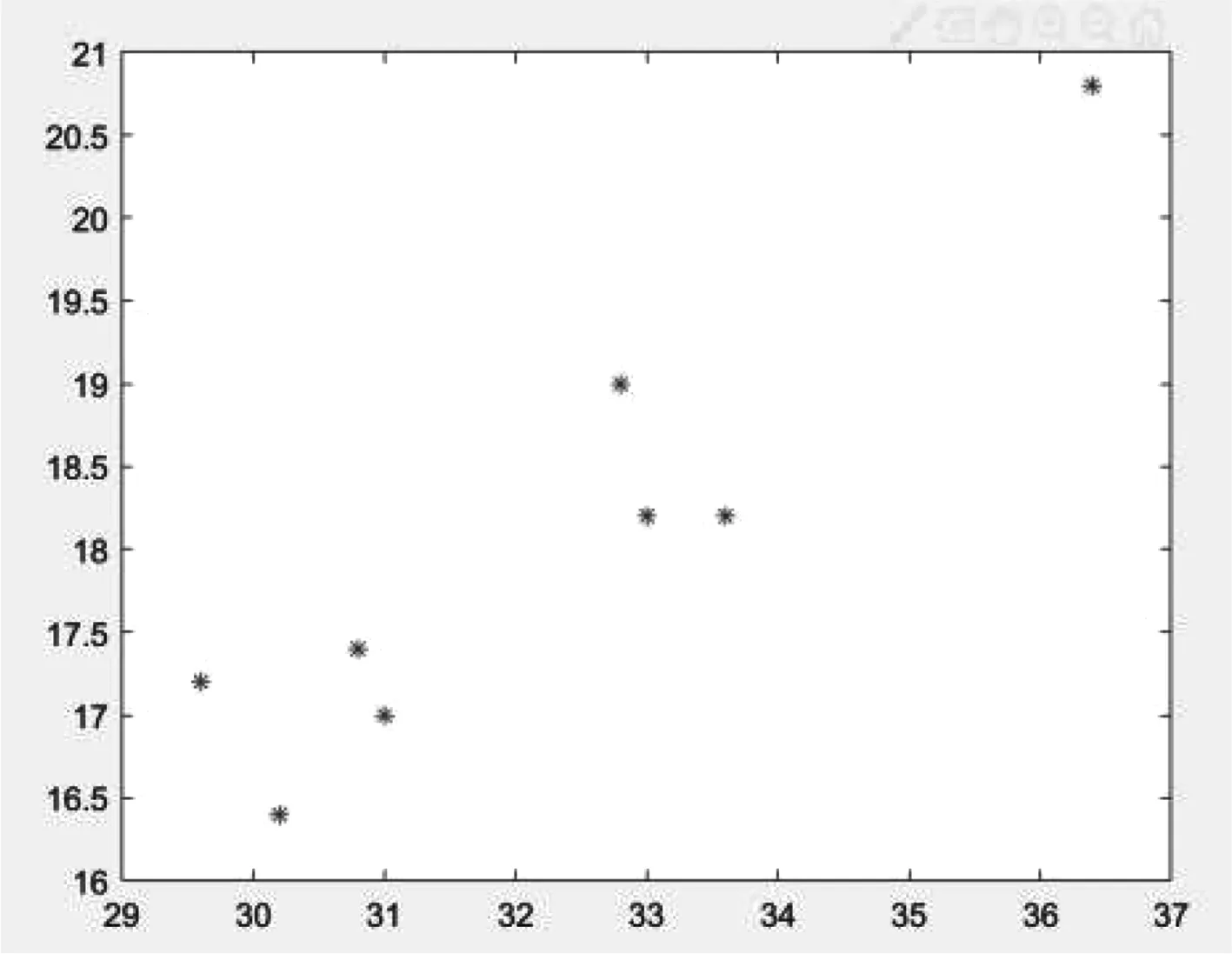
圖4 B類鳥散點圖Fig.4 Scattered plot of B type birds

圖5 所有鳥類散點圖Fig.5 Scattered plot of all birds

c.橫軸為翅展*身長，縱軸為身長。

圖6 A類鳥散點圖Fig.6 Scattered plot of A type birds

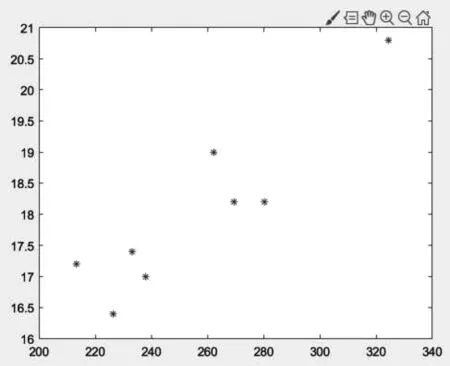
圖7 B類鳥散點圖Fig.7 Scattered plot of B type birds

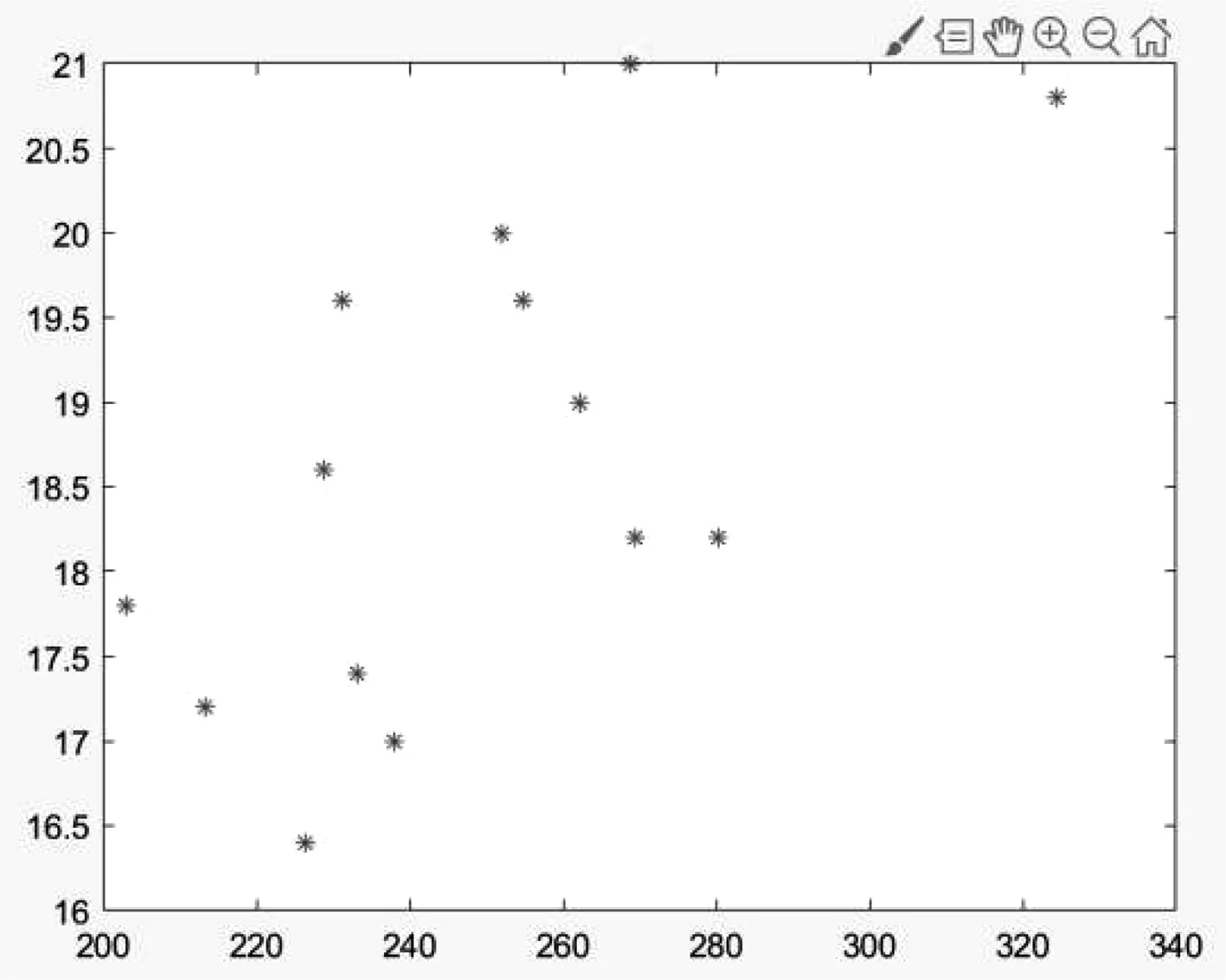
圖8 所有鳥類散點圖Fig.8 Scattered plot of all birds

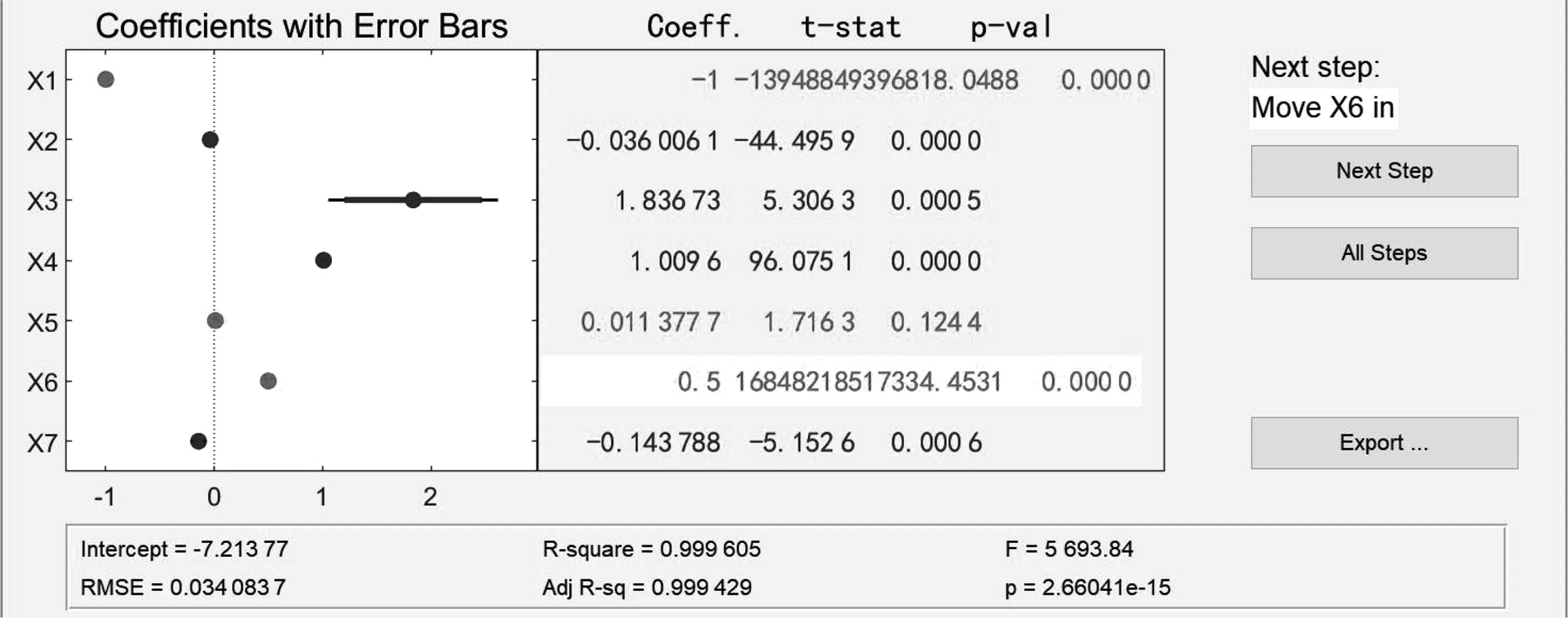
圖9 逐步回歸圖Fig.9 Stepwise regression

因為散點圖所反映的關系不明確，因此利用matlab系統工具箱中的逐步回歸命令stepwise實現逐步回歸[1]。

所加入的自變量：x1=x，x2=x^2，x3=s，x4=h，x5=m，x6=翅展與身長的差，x7=s.*x。其中x2=x^2，x3=s，x4=h，x7=s。

*x加入后，R^2接近于1，F值極大，p接近于0，模型較合適，因此考慮建立翅展的平方項、種類、翅展與身長的和項、種類與翅展的乘積項相關的模型。

利用matlab軟件建立模型：y = a + b×s + c×x.^2 + d×h + e×s×x

>> y=[17.80;19.60;18.60;20.00;21.00;19.60;17.20;17.40;16.40;19.00;17.00;18.20;18.20;20.80];

s=[1;1;1;1;1;1;0;0;0;0;0;0;0;0];

x=[11.40;11.80;12.30;12.60;12.80;13.00;12.40;13.40;13.80;13.80;14.00;14.80;15.40;15.60];

h=[29.20;31.40;30.90;32.60;33.80;32.60;29.60;30.80;30.20;32.80;31.00;33.00;33.60;36.40];

X=[ones(14,1),s,x.^2,h,s.*x];

[b,bint,r,rint,stats]=regress(y,X);

b,bint,stats

4.1.2 問題一的模型結果分析

利用excel軟件將結果列成表格。

表5 問題一的模型結果Tab.5 Modelling of Problem One

因變量的99.96%可由模型確定，F遠超過F檢驗的臨界值，p遠小于α=0.05，因此模型從整體上看成立。所有參數的置信區間均不包含零點。

模型結果：y=-7.213 8+1.836 7×s-0.036 0×x^2+1.009 6×h-0.143 8×s×x。

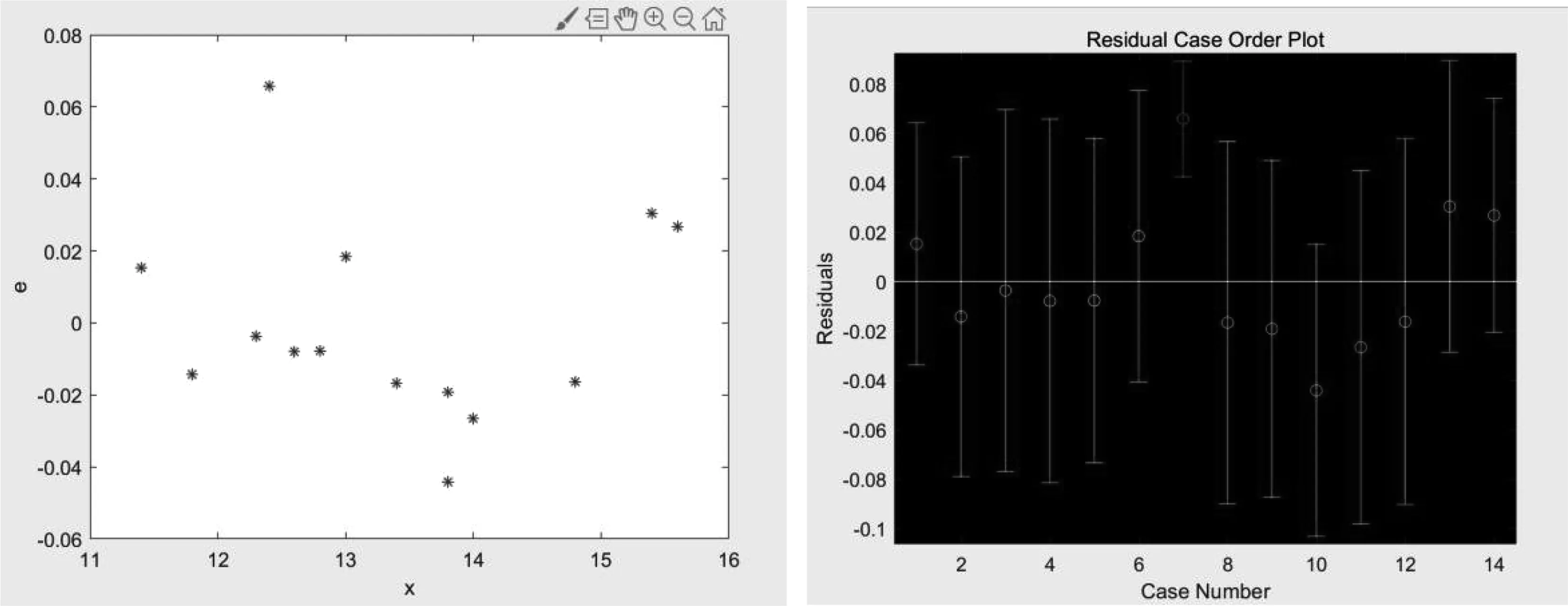
圖10 問題一中 X的殘差圖Fig.10 Residual plot of X in Problem One

4.1.3 問題一的改進模型建立

剔除1個異常數據，利用matlab進行新的回歸分析。

>>y=[17.80;19.60;18.60;20.00;21.00;19.60; 17.40;16.40;19.00;17.00;18.20;18.20;20.80];

s=[1;1;1;1;1;1;0;0;0;0;0;0;0];

x=[11.40;11.80;12.30;12.60;12.80;13.00; 13.40;13.80;13.80;14.00;14.80;15.40;15.60];

h=[29.20;31.40;30.90;32.60;33.80;32.60; 30.80;30.20;32.80;31.00;33.00;33.60;36.40];

X=[ones(13,1),s,x.^2,h,s.*x];

[b,bint,r,rint,stats]=regress(y,X);

b,bint,stats

4.1.4 問題一的改進模型結果分析

利用excel軟件將結果列成表格。

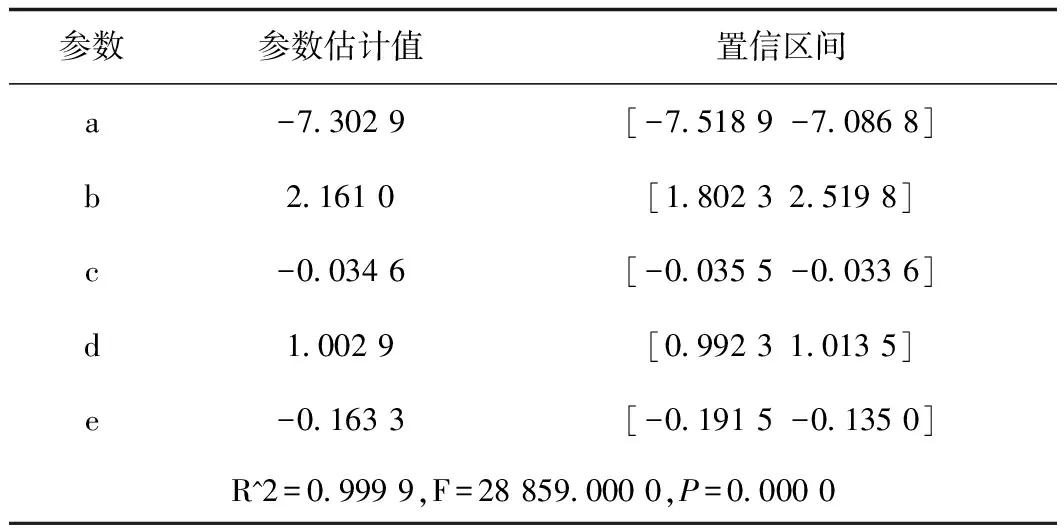
表6 問題一的改進模型結果Tab.6 Improved model results of Problem One

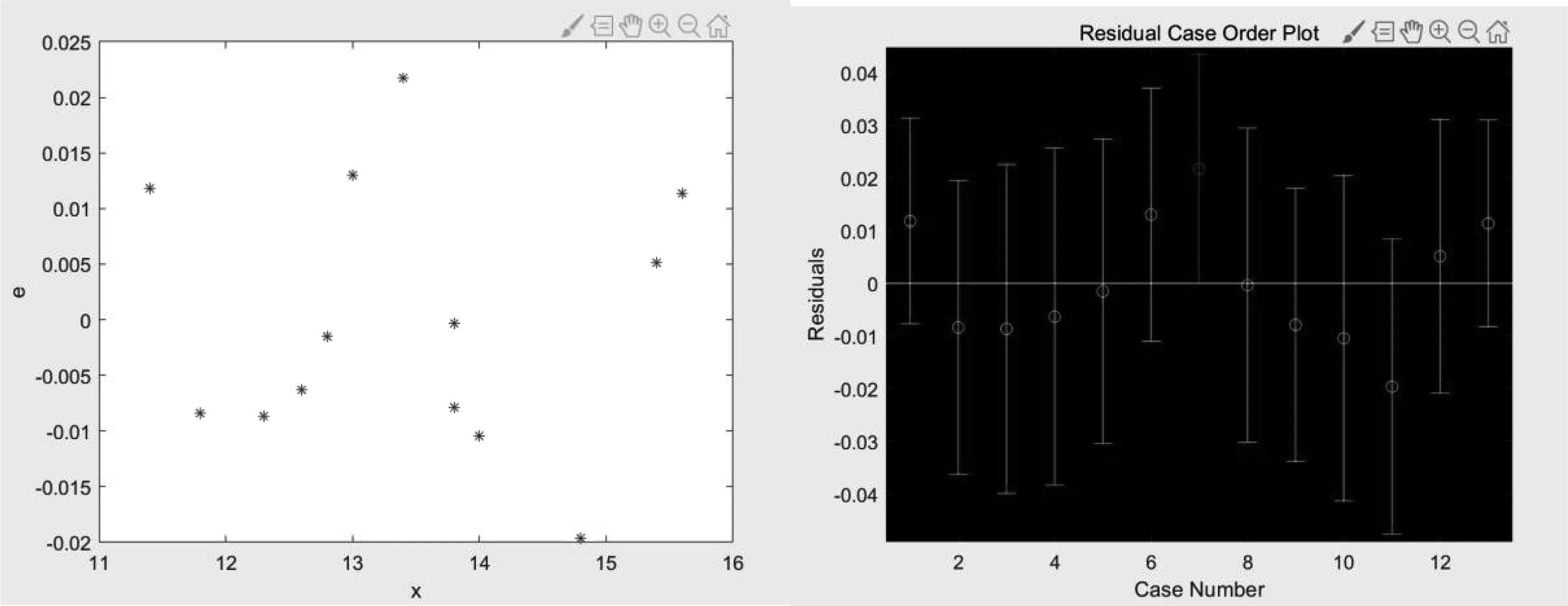
圖11 問題一中改進后X的殘差圖Fig.11 Residual plot of improved X in Problem One

改進后的模型結果：y=-7.302 9+2.161 0×s-0.034 6×x^2+1.002 9×h-0.163 3×s×x。

4.2 問題二求解

將(12.50，19.00)(13.00，18.00)(14.00，20.70)三組數據分別代入問題一中的模型，計算得到s的值，s大于等于0.5，則該鳥屬于A類；s小于0.5，則該鳥屬于B類。

利用excel列出表格。

表7 三只鳥的歸類Tab.7 Classification of three birds

4.3 問題三的模型建立與求解

4.3.1 問題三的模型建立

將(13.80，19.00)這組數據的s值更改為1，重新建立模型。

建立模型：y=a+b×s+c×x.^2+d×h+e×s×x

>>y=[17.80;19.60;18.60;20.00;21.00;19.60;17.20;17.40;16.40;19.00;17.00;18.20;18.20;20.80];

s=[1;1;1;1;1;1;0;0;0;1;0;0;0;0];

x=[11.40;11.80;12.30;12.60;12.80;13.00;12.40;13.40;13.80;13.80;14.00;14.80;15.40;15.60];

h=[29.20;31.40;30.90;32.60;33.80;32.60;29.60;30.80;30.20;32.80;31.00;33.00;33.60;36.40];

X=[ones(14,1),s,x.^2,h,s.*x];

[b,bint,r,rint,stats]=regress(y,X);

b,bint,stats

利用excel軟件將結果列成表格。

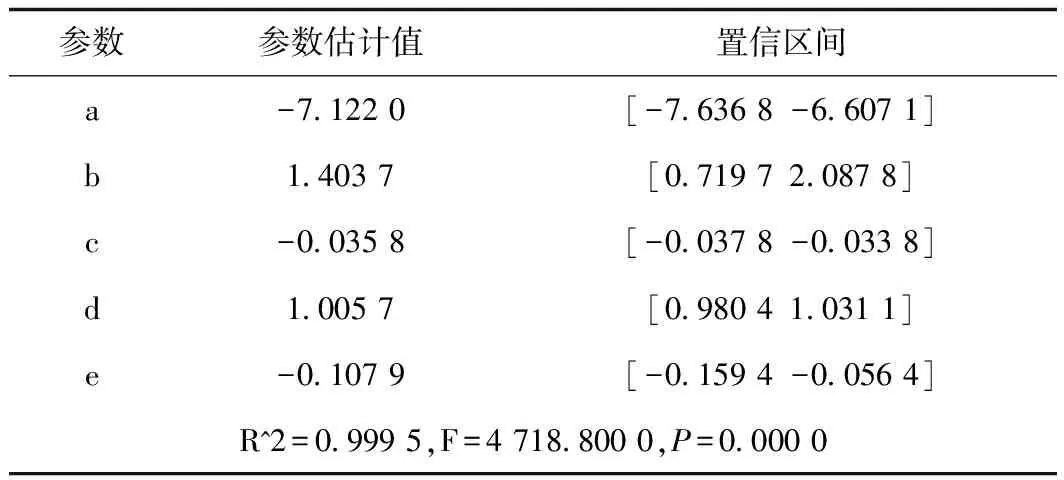
表8 問題三的模型結果Tab.8 Modelling of Problem Three

改正錯誤后的模型：y=-7.122 0+1.403 7×s-0.035 8×x^2+1.005 7×h-0.107 9×s×x[2]。

圖12 問題三中改進后X的殘差圖Fig.12 Residual plot of improved X in Problem Three

4.3.2 問題三結果分析

利用excel軟件將結果列成表格，與問題一所求得的模型數據進行對比。

表9 改正錯誤數據后的模型結果對比Tab.9 Comparison of modelling results after the modification of wrong data

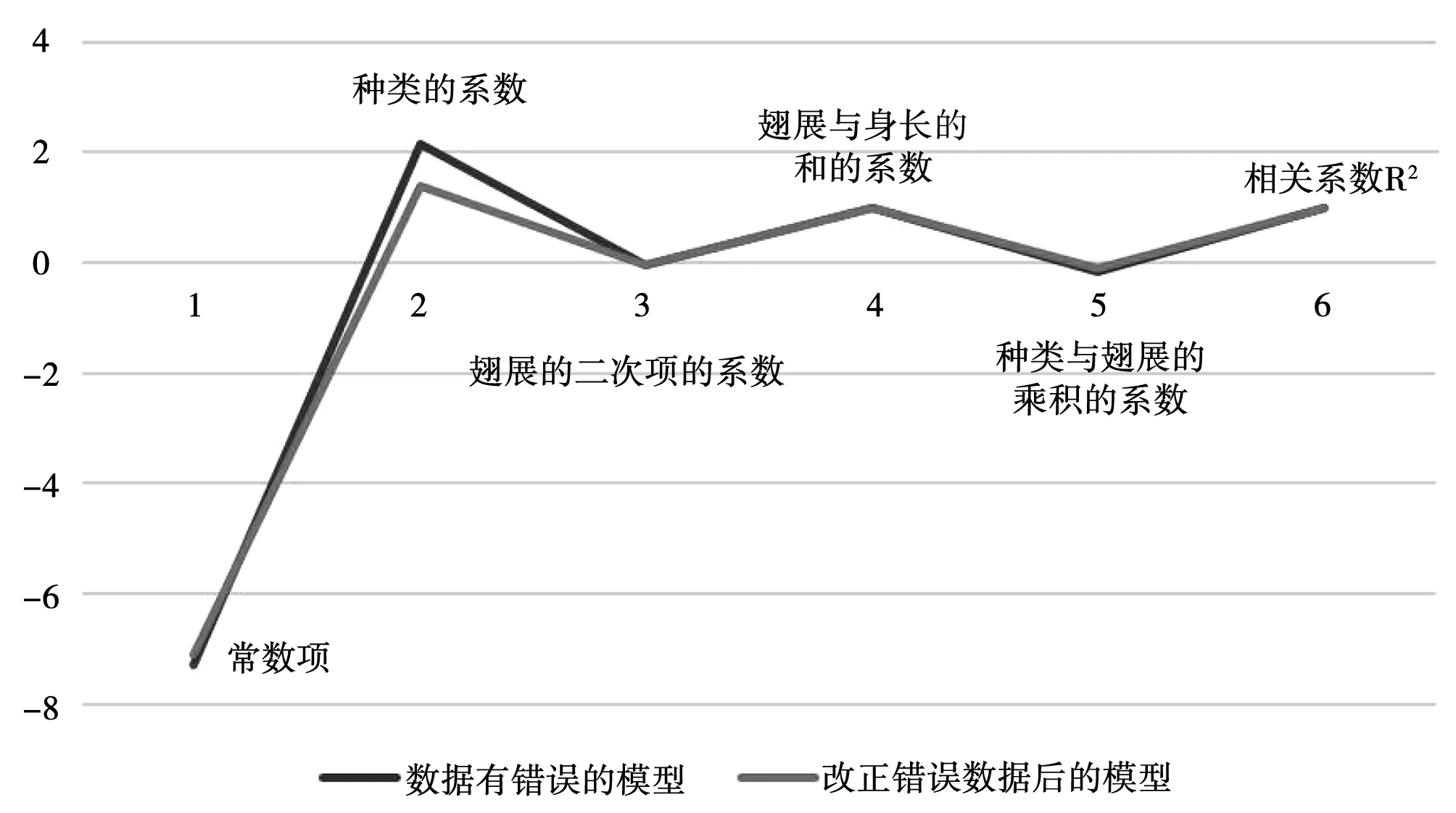
圖13 改正錯誤數據后的前后模型結果對比圖Fig.13 Comparison of modelling results before and after the modification of wrong data

與問題一中數據有錯誤的模型相比，改正錯誤數據后的模型的常數項較大，種類的系數較小，種類與翅展的積的系數較大，相關系數R^2較小，F值較小。

5 模型分析與改進

5.1 模型的優點

本建模運用逐步回歸法研究變量之間的關系，找到對因變量影響較為顯著的自變量，以此得到模型；本建模利用殘差分析法，將異常數據剔除，改進后的模型的相關系數R^2更接近1，F值更大，使模型得到改進；本建模中所有模型的置信區間均不包含零點[3]。

5.2 模型的缺點

由殘差圖可以看出，改進后的新模型仍存在異常數據；翅展的二次項的系數極接近于零，對因變量的影響較不顯著，應考慮采用其他自變量進行替代。

5.3 模型的改進

本研究只給出了一種改進后的統計回歸模型，還有更符合題目要求但未被發現的模型，因此應再給出幾種不同的改進模型，進行多角度的比較評價，從而尋找到更優的鳥類分類方案[4]。

6 結論與反思

6.1 結論

針對問題一：利用散點圖及逐步回歸法找到對因變量有顯著影響的自變量，得到鳥類翅展、身長等因素間的關系，建立統計回歸模型，并利用殘差分析法剔除異常數據以后對建立的模型進行改進。改進后的最終模型是：y=-7.302 9+2.161 0×s-0.034 6×x^2+1.002 9×h-0.163 3×s×x。

針對問題二：在問題一的基礎上，將題目中給出的3組數據依次代入問題一所得模型中，根據求得種類的值判斷該鳥是哪種鳥類。翅展和身長的數據為(12.50，19.00)的鳥是A類鳥；翅展和身長數據分別為(13.00，18.00)(14.00，20.70)的兩只鳥是B類鳥。

針對問題三：將錯誤數據對應種類的值進行更改，重新建立模型，對比修正后的結果與修正前的結果在回歸系數的點估計值、相關系數R^2、F值及與F對應概率p四方面的差異，從而得到該錯誤對分類的影響大小。改正錯誤后的新模型是：y=-7.122 0+1.403 7×s-0.035 8×x^2+1.005 7×h-0.107 9×s×x。與問題一中模型相比，改正錯誤數據后的模型常數項較大，種類系數較小，種類與翅展積的系數較大，相關系數R^2較小，F值較小。

6.2 反思

最開始建立模型時未利用好逐步回歸法，常局限于翅展和身長之間的關系，但是發現模型的相關系數R^2只有57.44%，F值也非常小。后建立的模型雖然相關系數等值都較為合適，但總會出現自變量置信區間包含零點的情況。之后，熟悉了逐步回歸法和matlab中stepwise命令的用法時，對于自變量的選取有了極大幫助。

剛開始列表格時常用word自帶表格，非常不方便，后來利用excel軟件可以更加快速簡潔地設立表格與圖表，使內容表述更加清晰直觀。