電動汽車驅動系統直流母線穩定性分析*

林 程，孫建俠，徐 垚，易 江

（北京理工大學，電動車輛國家工程實驗室，北京 100081）

前言

高壓系統是電動汽車的關鍵系統之一，其主要功能是將儲能設備產生的能量轉化為不同電壓等級和供電形式的電能，提供給車載電氣設備使用。電動汽車的高壓系統采用高壓直流供電架構，多種不同形式和性質的電源/負載集成于高壓直流母線上。每個電源/負載都可視為構成系統的基本單元，模塊化的設計方法提高了系統的可靠性和冗余度。在一項對美國大型運輸機的研究報告中，對高壓直流供電系統的供電質量、可靠性、維修性、費用和質量等方面進行了評價，綜合評分高達95.8。高壓直流供電系統具有明顯的技術優勢，在中壓船舶、多電飛機、直流微網等領域均有廣泛應用。

作為衡量高壓直流供電系統的唯一性能指標，母線電壓的品質直接影響著系統能否正常運行。針對直流母線電壓品質的評價，在通信、船舶等直流供電領域已經制定了相關標準。在美國海軍的直流電壓接口標準MIL?STD?1399中，對直流母線的電壓閃變、電壓波動、電壓偏差、紋波系數以及穩壓精度等指標做出了明確要求。這些標準為電動汽車高壓直流系統母線電壓品質評價提供了參考。目前，國際上對直流系統電壓穩定的普遍定義是：在系統受干擾時，直流母線電壓波動不超過系統額定值的±10%。

在當前電動汽車高壓直流系統集成過程中，各模塊往往是單獨設計后經過直流母線簡單互聯，忽略了模塊之間的耦合作用。盡管源/載側模塊能夠單獨穩定工作，集成后的系統卻可能發生母線失穩現象，這是因為采用嚴格閉環控制的電力電子變換器及所帶負載具有恒功率特性，而恒功率負載（constant power load，CPL）體現出負阻抗特性，直接導致系統的穩定性降低。當直流母線發生失穩時，母線電壓將出現大幅振蕩，超出正常波動范圍，容易觸發電路保護器件動作，嚴重時甚至導致系統崩潰。通過對某款國產電動客車進行故障數據統計發現其高壓系統故障占比達87.88%，遠超其他系統故障占比。因此，從系統的角度分析電動汽車高壓系統直流母線的穩定性，明確對接入負載的限制條件，并在此基礎上研究提高穩定性的方法，對于降低高壓系統故障、保證整車安全行駛具有重要的意義。

國內外的學者們對高壓直流供電系統穩定性分析方面進行了許多研究。海軍工程大學馬偉明院士團隊對中壓船舶直流供電系統的穩定性開展了深入分析，重點研究了發電機系統與推進負載的阻抗匹配問題，通過特征值靈敏度的方法評估了參數變化對系統穩定性的影響，為系統設計提供了依據。天津大學王成山教授課題組對直流微網母線電壓的穩定性分析與控制進行了大量研究，分別研究了由電源側下垂系數設置不當引起的低頻電壓振蕩問題和由CPL負載與LC濾波器級聯引起的高頻電壓振蕩問題，并搭建了實驗平臺進行穩定性分析與控制的驗證。北京航空航天大學的周元鈞教授開展了對多電飛機高壓直流供電系統穩定性的研究，分析了帶前端LC濾波器的驅動系統直流母線穩定性問題，并重點研究了LC濾波器及驅動控制器參數對直流母線瞬態特性的影響。加拿大麥克馬斯特大學的Ali Emadi教授課題組深入研究了電動汽車高壓直流系統的穩定性問題，將電驅動系統等效為CPL負載模型，采用相平面法分析了電源系統帶CPL負載時的母線電壓穩定性，為源側變換器設計提供了準則。

現有電動汽車高壓直流母線穩定性分析方法中，大多將驅動負載簡單等效為恒流源，重點分析源側變換器對母線電壓穩定性的影響。由于等效模型僅在低頻域內有效，并不能表征負載的全部頻率特性，且在此基礎上推導得出的負載限制條件準確度不高。針對這些問題，本文對源側變換器也進行了等效處理，著重分析了驅動系統負載對母線電壓穩定性的影響。采用能夠表征負載頻率特性的輸入導納模型進行穩定性分析，所得負載限制條件準確度更高。此外，為提高系統穩定性，提出了源/載側阻抗匹配的調節方法，并結合具體電動汽車實例進行了阻抗匹配設計。最后，通過實車實驗驗證了所提方案的有效性。

1 高壓直流系統

本文研究的電動汽車高壓直流系統結構如圖1所示，整個系統由電源系統、驅動系統和輔助系統構成。電動汽車的電源系統存在多種不同形式，燃料電池需要經高壓DC/DC變換器連接至高壓直流母線，蓄電池則通常直連在母線上。單個電源或多個電源復合后連接至高壓直流母線，為整車用電設備提供電能。高壓直流母線的用電設備包括驅動系統負載和幅值系統負載。其中，驅動系統負載包括DC/AC逆變器、控制器和驅動電機，是電動汽車最主要的系統之一。輔助系統包括輔助電機系統（轉向電機、制動電機）、空調系統、低壓電源系統、PTC加熱器等，用于提高電動汽車的操縱性和舒適性。

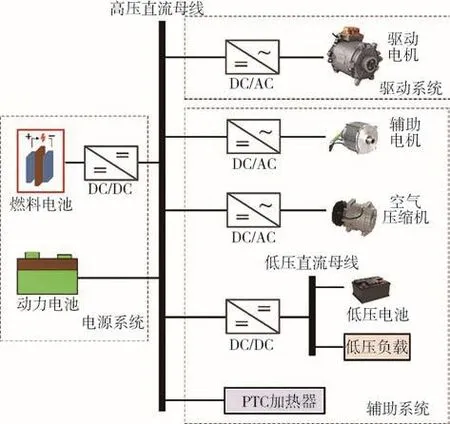
圖1 電動汽車高壓直流系統結構

2 阻抗模型

2.1 系統傳遞函數模型

圖1所示的高壓直流系統是一個復雜的非線性系統，直接對其進行穩定性研究不僅十分困難，也不利于發掘穩定性作用機理。因此，本文采用小信號穩定分析法，通過對系統穩態工作點進行線性化處理，降低高壓直流系統的非線性度，在此基礎上進行穩定性分析，為實際系統的穩定運行提供理論依據。

由美國加州理工學院Middlebrook教授提出的阻抗分析法被廣泛應用于直流系統的小信號穩定性分析中。整個高壓直流系統可以分為電源和負載兩個部分，等效電路如圖2所示。直流母線電壓的傳遞函數可以表示為

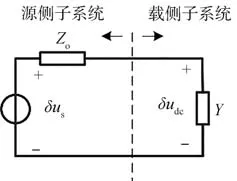
圖2 系統等效電路圖

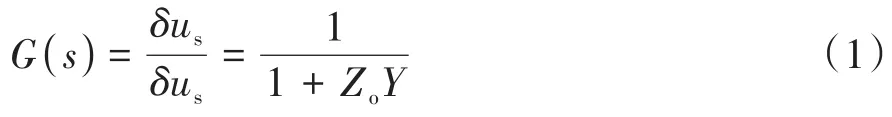
式中：與為電源電壓與母線電壓的小信號分量；為源側輸出阻抗；為載側輸入導納。上式中代表源側與載側系統的阻抗比，反映了兩個子系統之間的影響。

此外，由式（1）可以看出為直流母線電壓的開環傳遞函數。根據Nyquist判據，為使系統穩定，在復平面的Nyquist曲線應不包圍（?1，j0）點。因此，Middlebrook教授提出若的幅值在整個頻域范圍內均小于1，則系統一定符合Nyqsuit穩定判據 的 要 求，這 就 是 著 名 的 Middlebrook 穩 定判據。

2.2 源側輸出阻抗

直流電源經過高壓DC/DC變換器連接至高壓直流母線的電路結構如圖3所示，圖中，、、分別表示DC/DC變換器的電阻、電感、電容，為DC/DC變換器占空比，、分別為電源電壓和母線電壓，、分別為變換器輸入和輸出電流。

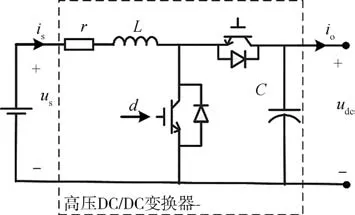
圖3 電源系統等效電路圖

根據電路原理建立如下高壓DC/DC變換器的狀態空間模型：

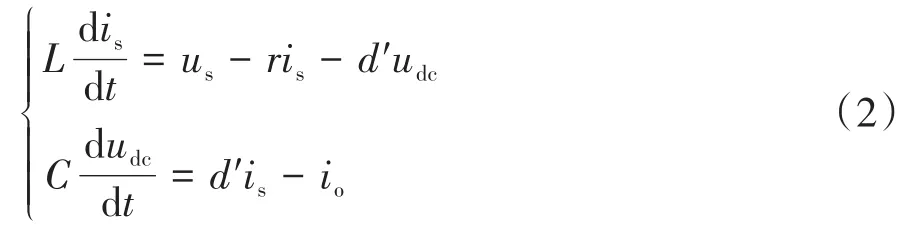
其中′=1?

根據文獻［23］所述DC/DC變換器建模方法，對式（2）進行小信號處理，得到小信號模型：

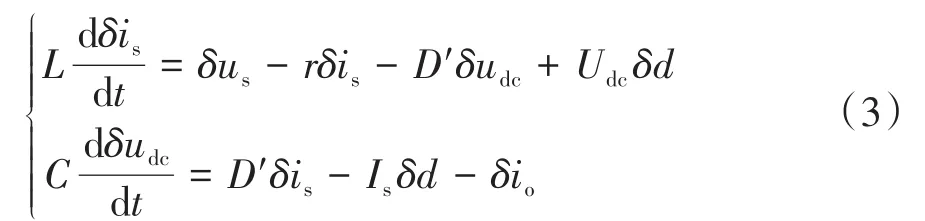
式中：前綴“”表示變量的小信號擾動；′=1?，為DC/DC變換器占空比穩態值；、分別為、的穩態值。

忽略電源及占空比擾動，令=0，=0，根據式（3）可以得到源側高壓DC/DC變換器的開環輸出阻抗為

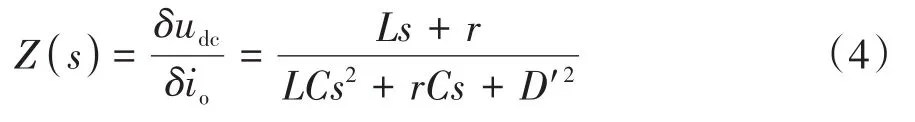
由上式可以看出，在諧振頻率處達到諧振幅值，容易超過系統穩定判據的限制。于是，此頻段也被稱為易失穩區。根據文獻［24］中的分析結果，DC/DC變換器引入閉環控制后，能夠抑制輸出阻抗在諧振頻率處的幅值尖峰，提高系統穩定性。由此可以看出，若開環系統滿足系統穩定判據要求，則閉環系統也一定滿足穩定性要求。因此，本文將根據穩定性更為苛刻的開環輸出阻抗模型進行穩定性分析。

對于并聯在直流母線上的蓄電池組可以等效為理想電源串聯電阻和電容的Thevenin模型，為簡化模型復雜程度，忽略電池內阻的影響，將蓄電池的輸出阻抗等效為電容。將所有并聯在高壓直流母線上的電容器包括蓄電池等效電容、負載逆變器直流支撐電容合并為一個電容器，與高壓DC/DC變換器的輸出阻抗并聯后，可以得到電源系統的輸出阻抗為

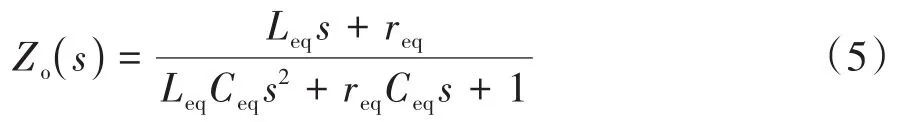
式中、、表示等效電阻、電感與電容，且有=/′，=/′，=+。

2.3 載側輸入導納

電動汽車的高壓直流母線與多種不同性質的負載相連，其中驅動系統的功率占比遠高于其余輔助系統的功率占比，是影響高壓直流母線穩定性最主要的因素。因此，本文將重點分析驅動系統負載對高壓母線穩定性的影響。整個驅動系統的電路拓撲結構如圖4所示，逆變器采用三相電壓型逆變器，驅動電機采用永磁同步電機（permanent magnet synchronous motor，PMSM），控制器采用磁場定向矢量控制（field?oriented control，FOC）策略，采集電機轉速、交流電流及母線電壓等信息，并根據給定信號輸出PWM開關調制信號控制逆變器實現電機調速控制。

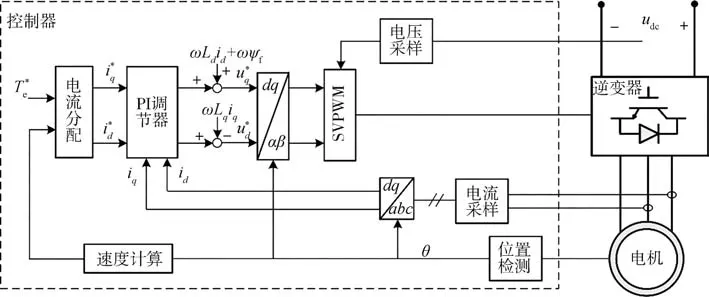
圖4 驅動系統的整體框圖

驅動系統包含了許多不同時間尺度的變量，如圖5所示。對于這樣時間尺度跨度大的系統，其全系統詳細數學模型十分復雜，難以用于穩定性分析研究。因此，本文以電磁時間尺度作為建模基礎，將機電時間尺度和中長期時間尺度的變量均看作恒定值，忽略其動態變化的影響。在此基礎上，根據文獻［26］中所示建模方法推導得到驅動系統的輸入導納模型。

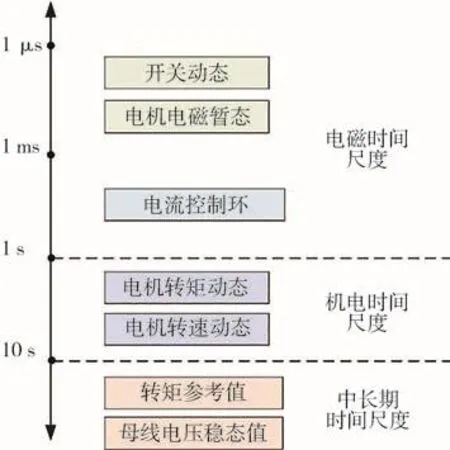
圖5 驅動系統時間尺度示意圖

根據功率平衡原理，在忽略逆變器的功率損耗時，有

式中：、分別為母線電壓與電流；u、u分別為軸定子電壓；i、i分別為軸定子電流。

根據小信號分析法對上式進行化簡，可以求得輸入導納為

式中：I、I為i、i的穩態工作點；U、U為u、u的穩態工作點；、為、的穩態工作點。前綴“”表示對應變量的小信號擾動。

根據驅動系統各模塊的工作原理及數學關系可以建立整個系統的小信號模型，如圖6所示，圖中D、D為軸逆變器占空比穩態值，為定子電阻，L、L為軸電感，為永磁體磁鏈，為電機電角速度，表示電流環PI調節器，且有=+K/s，、分別為比例和積分系數。根據圖示數學關系，可以求得

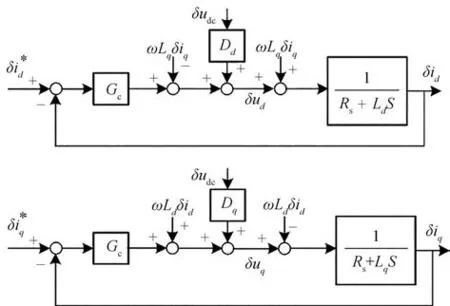
圖6 驅動系統小信號模型

將式（8）代入式（7）中可以求得驅動系統的輸入導納為

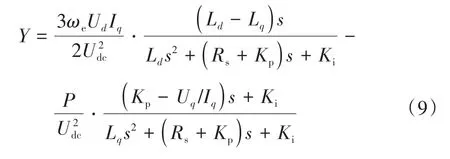
式中為負載功率，=。

可以看出包含兩個部分，等號右側第一項表示軸導納Y，第二項表示軸導納Y。可以看出Y具有負導納特性，Y為正導納。Y的存在能夠使驅動系統的負阻抗特性減弱，系統穩定性提高。驅動電機為表貼式PMSM時，軸導納Y為0，系統輸入導納=Y，穩定性要更加苛刻。因此，本文以表貼式PMSM模型為基礎進行穩定性分析，此時驅動系統輸入導納可以簡化為

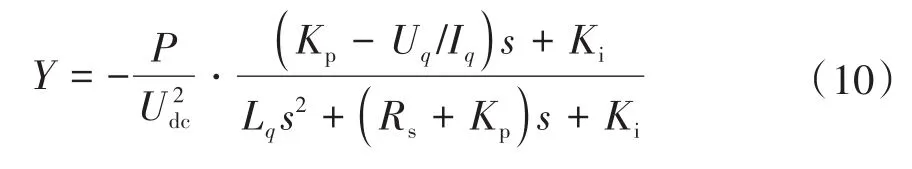
3 穩定性分析

源側輸出阻抗與載側輸入導納的頻率特性曲線如圖7所示，其中ω為的諧振頻率，ω為的轉折頻率：

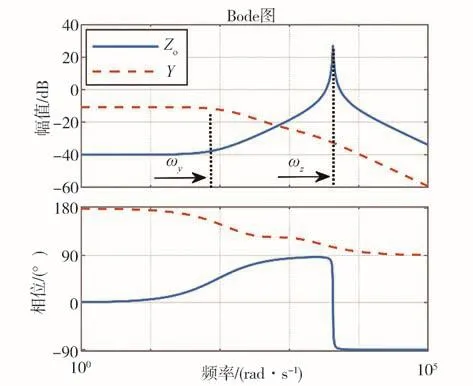
圖7 Z o與Y頻率特性曲線

的帶寬接近電流內環的帶寬，通常在幾十至幾百Hz，遠小于源側阻抗的諧振頻率，即有ω<<ω。由圖7可以看出，在ω頻率處達到諧振幅值，且的諧振幅值為

在ω頻率處達到諧振幅值，且的諧振幅值為

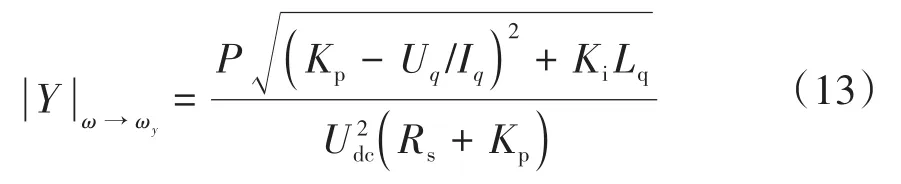
根據Middlebrook穩定判據的要求，阻抗比的幅值應始終小于1。由于的幅值不超過與諧振幅值的乘積，即有

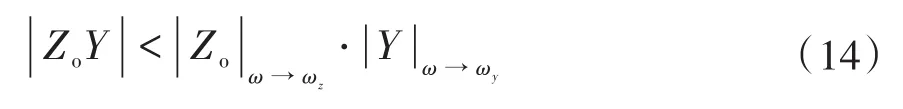
因此，通過令與諧振幅值的乘積小于1，即可使系統滿足穩定性要求。將式（12）和式（13）代入式（14）中化簡可以得到系統穩定條件：

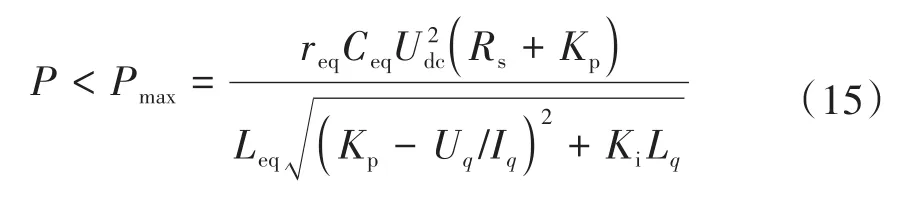
式中表示直流母線準入的負載功率限制。

上述穩定條件對接入直流母線的驅動系統功率提出了限制要求。負載功率滿足穩定條件時，直流母線電壓能保持穩定，負載功率超過限制時容易造成母線電壓振蕩問題。

根據之前的分析可以看出母線電壓系統穩定性與源載側阻抗比有關，通過合理地配置源/載側阻抗，減小的幅值，可以增加系統穩定裕量，提高母線電壓品質。阻抗匹配可以通過降低源側阻抗幅值或降低載側導納幅值來實現。其中，源側阻抗與硬件阻尼有關，通過降低電感值、提高電阻值和電容值等方法可以降低的諧振幅值，如圖8所示。載側導納與母線電壓、電機硬件及控制器等參數有關，電機硬件在設備選型時已經確定。提高母線電壓等級可以降低的負阻抗特性，減小整個頻域內的幅值，如圖9所示。根據式（10）可以看出，的值直接影響在中高頻段的幅值，當的值接近U/I時，可以降低在中高頻段的幅值，如圖10所示。因此，提高系統穩定裕量的方法包括：（1）提高源側阻尼；（2）提高母線電壓等級；（3）合理配置載側控制器PI參數。

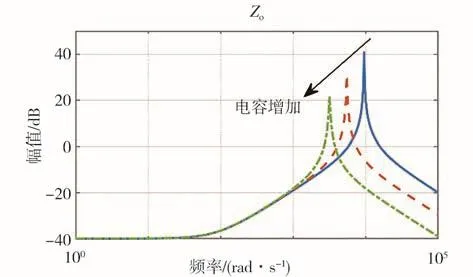
圖8 電容增加時源側阻抗幅值變化

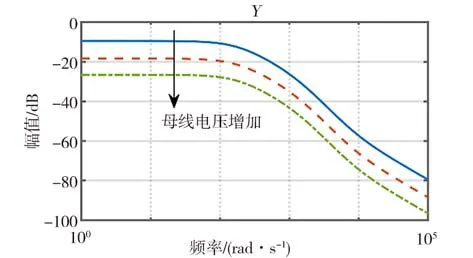
圖9 母線電壓增加時載側導納幅值變化

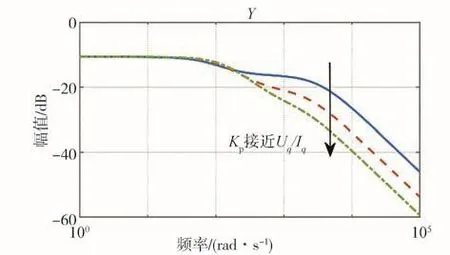
圖10 K p接近Uq/Iq時源載側幅值變化

4 實驗驗證

本節將結合具體電動汽車實例進行穩定性分析，根據實車工況數據驗證前述分析結論。電動汽車高壓直流系統的直流電源為燃料電池，輸出電壓為150 V。燃料電池經高壓DC/DC變換器后連接至高壓直流母線，輸出功率為40 kW。高壓DC/DC變換器采用雙向DC/DC變換器，其開關頻率為80 kHz。此外，為提高直流母線電壓品質，母線上并聯蓄電池組，容量為96 A·h，標稱電壓為627.6 V。驅動系統采用三相電壓源型逆變器，開關頻率為10 kHz。驅動電機為PMSM，額定轉矩為550 N·m，峰值轉速為4 500 r/min，額定功率為110 kW，峰值功率為175 kW。高壓直流系統各個模塊的參數設置詳見表1。

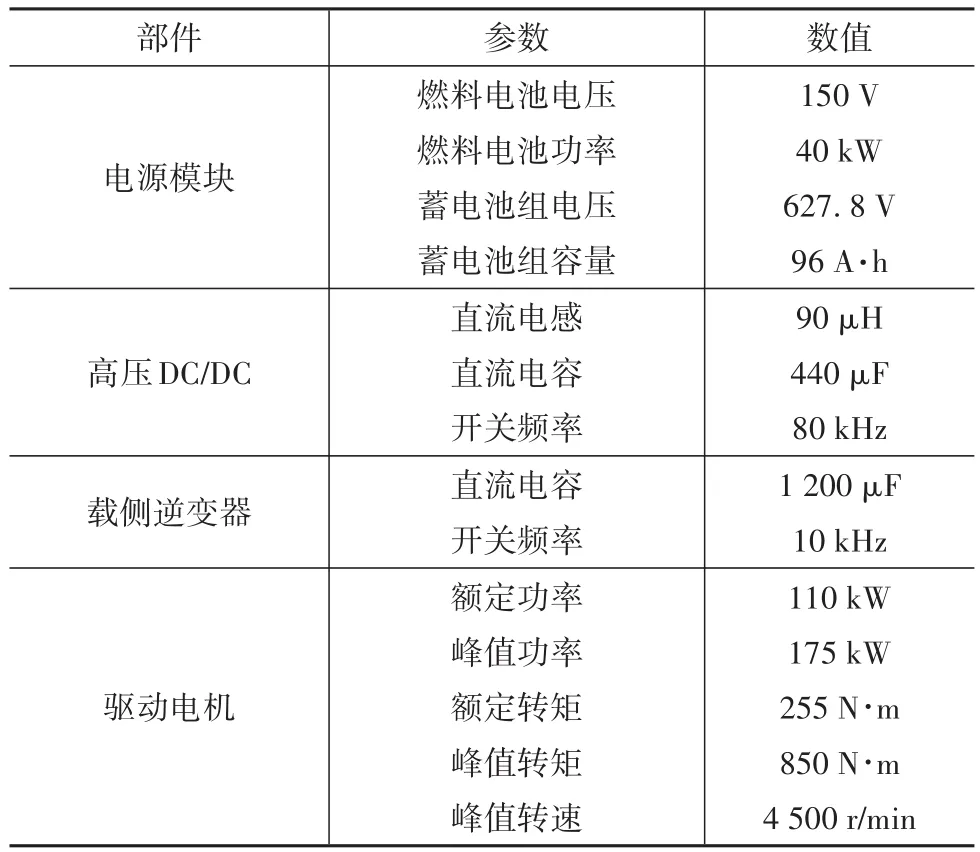
表1 高壓直流系統參數

根據式（15）和表1所示參數，得出負載實際運行功率與限制功率的關系，如圖11所示。可以看出，電機運行功率始終小于限制功率，母線電壓能夠保證穩定。為了驗證所述分析結論，進行了實車驗證。電動汽車行駛在延慶區的盤山公路，行駛工況包括連續彎道、上下坡等山區工況。燃料電池、蓄電池組及驅動負載功率變化如圖12（a）所示，在實車運行過程中，燃料電池提供恒定輸出功率，蓄電池組根據驅動系統的功率需求提供波動功率，能夠起到削峰填谷作用，抑制負載功率變化對母線電壓的沖擊。

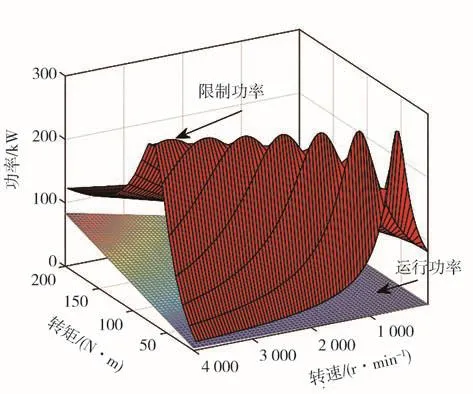
圖11 負載限制功率與實際運行功率關系

圖12（b）所示為母線電壓波形，母線電壓最大值為654.2 V，最小值為635.4 V，母線電壓波動為18.8 V。根據直流電壓接口標準MIL?STD?1399的要求，穩態時母線電壓波動應小于±4%，因此，高壓母線電壓波動應小于25.6 V。可以看出，圖12（b）所示電壓波動符合標準要求，母線電壓穩定。

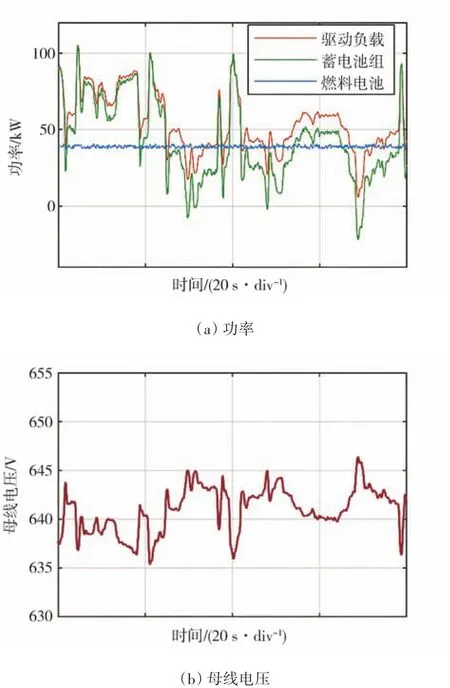
圖12 實車測量結果

5 結論

本文基于系統阻抗模型推導了直流母線電壓全頻域穩定條件，并由此對負載功率提出了限制要求。阻抗模型能夠描述負載的頻率特性，因此所得穩定條件能夠保證母線電壓在整個頻域范圍內的穩定性，準確度更高。通過源/載側阻抗匹配可以提高母線電壓品質，方法包括：（1）提高源側阻尼；（2）提高母線電壓等級；（3）合理配置載側控制器PI參數。穩定性分析結論通過具體實例得到了驗證，為系統的硬件和控制器參數設計提供了參考依據，有助于改善和提升高壓系統的穩定性能。